算法通关村第十九关——动态规划高频问题(白银)
算法通关村第十九关——动态规划高频问题(白银)
- 前言
- 1 最少硬币数
- 2 最长连续递增子序列
- 3 最长递增子序列
- 4 完全平方数
- 5 跳跃游戏
- 6 解码方法
- 7 不同路径 II
前言
摘自:代码随想录
动态规划五部曲:
- 确定dp数组(dp table)及其下标的含义
- 确定递推公式
- 初始化dp数组
- 确定遍历顺序
- 举例推导dp数组
1 最少硬币数
leetcode 322. 零钱兑换
动规五部曲分析如下:
- 确定dp数组以及下标的含义
dp[j]:凑足总额为 j 所需钱币的最少个数为dp[j]
- 确定递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],
那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
- dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
其他下标对应的数值呢?
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。
int[] dp = new int[amount + 1];
// 往数组dp里面填充某个数,这里选择amount+1,就是最大的值
Arrays.fill(dp, amount+1);
dp[0] = 0;
- 确定遍历顺序
有两种方式:
第一种:外循环遍历金额,内循环遍历硬币面额。
第二种:外循环遍历硬币面面额,内循环遍历金额。
这两种遍历顺序对应的意义如下:
-
外循环遍历金额,内循环遍历硬币面额:
这种遍历顺序的意义是在计算找零过程中,我们首先考虑金额的变化,然后再考虑不同的硬币面额。
也就是说,我们固定一个金额,尝试使用不同的硬币面额来找零。这样做的好处是可以利用之前已经计算出来的金额的最少硬币数,快速得到当前金额的最优解。由于金额是从小到大递增的,所以我们在计算每个金额的最优解时,可以利用前面较小金额的最优解已经被计算出来的特点。
// 遍历金额
for (int i = 1; i <= amount; i++) {// 遍历硬币面额for (int j = 0; j < coins.length; j++) {if (coins[j] <= i) {dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);}}
}
-
外循环遍历硬币面额,内循环遍历金额:
这种遍历顺序的意义是在计算找零过程中,我们首先考虑不同的硬币面额,然后再考虑不同的金额。
也就是说,我们固定一个硬币面额,尝试在不同的金额下进行找零。这样做的好处是可以保证我们将所有可能的硬币面额都考虑到,并且在计算每个金额的最优解时,可以利用之前已经计算出来的较小金额的最优解。由于硬币面额是从小到大递增的,所以我们在计算每个金额的最优解时,可以利用之前较小硬币面额的最优解已经被计算出来的特点。
// 遍历硬币面额
for (int coin : coins){// 遍历金额for (int i = 1; i <= amount; i++) {if(coin <= i){dp[i] = Math.min(dp[i], dp[i - coin] + 1);}}
}
全部代码如下:
第一种:
class Solution {public int coinChange(int[] coins, int amount) {// 初始化dp数组int[] dp = new int[amount + 1];Arrays.fill(dp, amount + 1);dp[0] = 0;// 遍历金额for (int i=1; i <= amount; i++) {// 遍历硬币面额for (int j=0; j < coins.length; j++){if(coins[j] <= i){dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);}}}return dp[amount] > amount ? -1 : dp[amount];}
}
第二种:
class Solution {public int coinChange(int[] coins, int amount) {// 初始化dp数组int[] dp = new int[amount + 1];Arrays.fill(dp, amount + 1);dp[0] = 0;// 遍历硬币面额for (int coin : coins){// 遍历金额for (int i = 1; i <= amount; i++) {if(coin <= i){dp[i] = Math.min(dp[i], dp[i - coin] + 1);}}}return dp[amount] > amount ? -1 : dp[amount];}
}
2 最长连续递增子序列
leetcode 674. 最长连续递增序列
动规五部曲分析如下:
- 确定dp数组以及下标的含义
dp数组:表示以当前元素为结尾的最长连续递增序列的长度。
dp[i]表示以nums[i]为结尾的最长连续递增序列的长度。
- 确定递推公式
如果nums[i] > nums[i-1],则dp[i] = dp[i-1] + 1;否则dp[i] = 1。
- dp数组如何初始化
我们将dp数组的所有元素初始化为1,因为每个元素都可以作为一个单独的递增序列。
- 确定遍历顺序
从第二个元素开始遍历:
for(int i=0; i < nums.length; i++){if(i > 0 && nums[i] > nums[i-1]){dp[i] = dp[i-1] + 1;}else{dp[i] = 1;}
}
- 举例说明
举例说明:给定数组nums = [1, 3, 5, 4, 7]。
遍历过程如下:
- 对于nums[1] = 3,nums[0] = 1 < nums[1],所以dp[1] = dp[0] + 1 = 2。
- 对于nums[2] = 5,nums[1] = 3 < nums[2],所以dp[2] = dp[1] + 1 = 3。
- 对于nums[3] = 4,nums[2] = 5 > nums[3],所以dp[3] = 1。
- 对于nums[4] = 7,nums[3] = 4 < nums[4],所以dp[4] = dp[3] + 1 = 2。
最终的最长连续递增序列的长度为dp数组的最大值,即为3。
最后代码如下:
class Solution {public int findLengthOfLCIS(int[] nums) {if (nums == null || nums.length == 0) {return 0;}int[] dp = new int[nums.length];dp[0] = 1;for(int i=1; i < nums.length; i++){if(nums[i] > nums[i-1]){dp[i] = dp[i-1] + 1;}else{dp[i] = 1;}}return Arrays.stream(dp).max().getAsInt();}
}
不是使用stream的方式:
class Solution {public int findLengthOfLCIS(int[] nums) {if (nums == null || nums.length == 0) {return 0;}int[] dp = new int[nums.length];dp[0] = 1;int maxLength = 1;for(int i=1; i < nums.length; i++){if(nums[i] > nums[i-1]){dp[i] = dp[i-1] + 1;}else{dp[i] = 1;}maxLength = Math.max(maxLength, dp[i]);}return maxLength;}
}
还可以得到dp[i],再遍历一遍得到最大值,这就不写了
3 最长递增子序列
leetcode 300. 最长递增子序列
-
确定dp数组(dp table)及其下标的含义:
- dp数组:dp[i] 表示以第i个数字结尾的最长递增子序列的长度。
- 下标的含义:dp[i] 表示以第i个数字结尾的最长递增子序列的长度。
-
确定递推公式:
- 如果nums[i] > nums[j],则:dp[i] = max(dp[i], dp[j] + 1)。
为啥呢??
这里的i和j表示数组
nums的索引。具体来说,i表示当前遍历到的元素的索引,而j表示在i之前的元素的索引。当我们遍历到第i个元素时,我们需要寻找在i之前的元素中比nums[i]小的元素。这样,我们就可以利用这个小于nums[i]的元素来构成一个更长的递增子序列。
所以,当nums[i] > nums[j]时,表示nums[i]比nums[j]大,我们可以将以j结尾的最长递增子序列的长度加1,然后与以i结尾的最长递增子序列的长度进行比较,取较大的值作为以i结尾的最长递增子序列的长度。也就是递推公式中的
dp[i] = max(dp[i], dp[j] + 1)。 -
初始化dp数组:
- 初始时,dp数组中的每个元素都设为1,因为最短的递增子序列长度为1。
-
确定遍历顺序:
- 外层循环遍历数组nums,从左到右依次计算dp[i]的值。
- 内层循环遍历数组nums,从数组开始到i的位置,寻找前面的数字nums[j]是否小于nums[i],如果是,则根据递推公式更新dp[i]的值。
-
举例推导dp数组:
如果nums[i] > nums[j],则dp[i] = max(dp[i], dp[j] + 1)。
逐个元素计算dp[i]的值:
- 当i = 1时,nums[i] = 9,此时没有比9小的元素,所以以9结尾的最长递增子序列长度仍为1。
nums: 10 9 2 5 3 7 101 18
dp: 1 1 1 1 1 1 1 1- 当i = 2时,nums[i] = 2,此时在2之前有9和10两个元素,都比2大,所以以2结尾的最长递增子序列长度仍为1。
nums: 10 9 2 5 3 7 101 18
dp: 1 1 1 1 1 1 1 1- 当i = 3时,nums[i] = 5,此时在5之前有2和9两个元素,其中2比5小,所以以5结尾的最长递增子序列长度为dp[2] + 1 = 2。
nums: 10 9 2 5 3 7 101 18
dp: 1 1 1 2 1 1 1 1- 当i = 4时,nums[i] = 3,此时在3之前有2和5两个元素,其中2比3小,所以以3结尾的最长递增子序列长度为dp[2] + 1 = 2。
nums: 10 9 2 5 3 7 101 18
dp: 1 1 1 2 2 1 1 1
后面略~~~~~~
完整代码如下:
class Solution {public int lengthOfLIS(int[] nums) {if (nums == null || nums.length == 0) {return 0;}int n = nums.length;int[] dp = new int[n];dp[0] = 1; int result = 1; for (int i = 1; i < n; i++) {dp[i] = 1; for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) { dp[i] = Math.max(dp[i], dp[j] + 1); }}result = Math.max(result, dp[i]); }return result;}
}
4 完全平方数
leetcode 279. 完全平方数
动态规划五部曲:
- 确定dp数组(dp table)及其下标的含义
**dp[i]:**表示数字i的最少完全平方数的个数。
- 确定递推公式
对于数字 i 来说,我们需要遍历所有小于等于 i 的完全平方数 j( j 从 1 到 sqrt(i) ),然后将当前数字 i 减去 j 得到差值,即 i - j 。我们需要找到 dp[ i - j * j ] 的最小值,然后再加上1(表示当前完全平方数 j ),即可得到dp[i]的值。
递推公式为:dp[i] = Math.min(dp[i], dp[i - j * j] + 1),其中 j * j <= i。
- 初始化dp数组
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
- 确定遍历顺序
// 遍历dp数组
for (int i = 1; i <= n; i++) {// 遍历小于等于i的完全平方数j*jfor (int j = 1; j * j <= i; j++) {// 更新dp[i]dp[i] = Math.min(dp[i], dp[i - j * j] + 1);}
}
- 举例推导dp数组
略。。。
完整代码:
class Solution {public int numSquares(int n) {// 定义dp数组int[] dp = new int[n + 1];// 初始化dp数组Arrays.fill(dp, n+1);dp[0] = 0;// 遍历dp数组for (int i = 1; i <= n; i++) {// 遍历小于等于i的完全平方数j*jfor (int j = 1; j * j <= i; j++) {// 更新dp[i]dp[i] = Math.min(dp[i], dp[i - j * j] + 1);}}return dp[n]; }
}
当然,这个代码可以再优化一下:(使用Math的api)
减少内层循环的次数:对于小于等于 i 的完全平方数 j ,我们可以通过计算 i - j * j 的平方根得到 j 的最大值,并从最大值开始遍历,这样可以减少内层循环的次数。
class Solution {public static int numSquares(int n) {// 定义dp数组int[] dp = new int[n + 1];// 初始化dp数组Arrays.fill(dp, n + 1);dp[0] = 0;// 遍历dp数组for (int i = 1; i <= n; i++) {// 获取当前数字i的最大完全平方数j*jint maxSquare = (int) Math.sqrt(i);// 遍历完全平方数j*jfor (int j = maxSquare; j >= 1; j--) {// 更新dp[i]dp[i] = Math.min(dp[i], dp[i - j * j] + 1);}}return dp[n];}
}
5 跳跃游戏
leetcode 55. 跳跃游戏
动态规划五部曲:
- 确定dp数组(dp table)及其下标的含义
dp[i]表示从起点位置到达位置i时能否跳跃到最后一个位置。
- 确定递推公式
dp[i] = (dp[j] && nums[j] >= i - j),其中0 <= j < i
- 初始化dp数组
初始化dp数组所有位置为false。
- 确定遍历顺序
外层循环遍历i从1到n-1,内层循环遍历j从0到i-1。
- 举例推导dp数组
以数组nums = [2, 3, 1, 1, 4]为例进行推导:
初始状态:
dp = [false, false, false, false, false]
推导dp[1]:
dp[1] = (dp[0] && nums[0] >= 1 - 0) = (false && 2 >= 1) = false
推导dp[2]:
dp[2] = (dp[0] && nums[0] >= 2 - 0) || (dp[1] && nums[1] >= 2 - 1) = (false && 2 >= 2) || (false && 3 >= 2) = false
推导dp[3]:
dp[3] = (dp[0] && nums[0] >= 3 - 0) || (dp[1] && nums[1] >= 3 - 1) || (dp[2] && nums[2] >= 3 - 2) = (false && 2 >= 3) || (false && 3 >= 3) || (false && 1 >= 3) = false
完整代码如下:
class Solution {public boolean canJump(int[] nums) {// 获取数组长度int n = nums.length;// 定义dp数组boolean[] dp = new boolean[n];// 初始化dp数组dp[0] = true;// 遍历dp数组for (int i = 1; i < n; i++) {// 内层循环遍历jfor (int j = 0; j < i; j++) {// 更新dp[i]dp[i] = dp[j] && nums[j] >= i - j;// 如果dp[i]为true,则跳出内层循环if (dp[i]) {break;}}}return dp[n - 1];}
}
6 解码方法
leetcode 91. 解码方法
动态规划五部曲:
- 确定dp数组(dp table)及其下标的含义
dp[i]表示从字符串的起始位置到第i个字符时的解码方法总数。
- 确定递推公式
对于dp数组中的每个位置i,我们需要考虑两个情况:
- 如果第i个字符能够单独解码(即不为0),则dp[i] = dp[i-1],因为第i个字符自身可以作为一个解码方法;
- 如果第i个字符与前一个字符组成的两位数能够解码(即与前一个字符组成的数字在1到26之间),则dp[i] += dp[i-2],因为组成的两位数可以作为一个解码方法。
则,递推公式为:dp[i] = dp[i-1] + dp[i-2],其中0 <= i < n。
- 初始化dp数组
初始化dp数组的长度为n+1,初始值为0。
- 确定遍历顺序
for (int i = 1; i <= n; i++) {// 如果第i个字符能够单独解码(即不为0)if (s.charAt(i - 1) != '0') {dp[i] += dp[i - 1];}// 如果第i个字符与前一个字符组成的两位数能够解码(即与前一个字符组成的数字在1到26之间)if (i >= 2 && isValidEncoding(s.substring(i - 2, i))) {dp[i] += dp[i - 2];}
}
// 判断字符串编码是否在1到26之间
private static boolean isValidEncoding(String s) {if (s.charAt(0) == '0') {return false;}int num = Integer.parseInt(s);return num >= 1 && num <= 26;
}
- 举例推导dp数组
以字符串s = "226"为例进行推导:
初始状态:
dp = [1, 0, 0, 0]
推导dp[1]:
如果第1个字符为2,能够单独解码为"2",所以dp[1] = dp[0] = 1
推导dp[2]:
如果第2个字符为2,能够单独解码为"2",所以dp[2] = dp[1] = 1
如果第1个字符与第2个字符组成的两位数为26,能够解码为"26",所以dp[2] += dp[0],即dp[2] = dp[1] + dp[0] = 1 + 1 = 2
推导dp[3]:
如果第3个字符为6,能够单独解码为"6",所以dp[3] = dp[2] = 2
如果第2个字符与第3个字符组成的两位数为26,能够解码为"26",所以dp[3] += dp[1],即dp[3] = dp[2] + dp[1] = 2 + 1 = 3
最终结果:
dp = [1, 1, 2, 3]
完整代码:
class Solution {public static int numDecodings(String s) {// 获取字符串的长度int n = s.length();// 定义dp数组int[] dp = new int[n + 1];// 初始化dp数组dp[0] = 1;// 遍历dp数组for (int i = 1; i <= n; i++) {// 如果第i个字符能够单独解码(即不为0)if (s.charAt(i - 1) != '0') {dp[i] += dp[i - 1];}// 如果第i个字符与前一个字符组成的两位数能够解码(即与前一个字符组成的数字在1到26之间)if (i >= 2 && isValidEncoding(s.substring(i - 2, i))) {dp[i] += dp[i - 2];}}return dp[n];}// 判断字符串编码是否在1到26之间private static boolean isValidEncoding(String s) {if (s.charAt(0) == '0') {return false;}int num = Integer.parseInt(s);return num >= 1 && num <= 26;}
}
不过可以简化一下,就是比较难理解一点,意义一样滴:
class Solution {public int numDecodings(String s) {int n = s.length();int[] f = new int[n + 1];f[0] = 1;for (int i = 1; i <= n; ++i) {if (s.charAt(i - 1) != '0') {f[i] += f[i - 1];}if (i > 1 && s.charAt(i - 2) != '0' && ((s.charAt(i - 2) - '0') * 10 + (s.charAt(i - 1) - '0') <= 26)) {f[i] += f[i - 2];}}return f[n];}
}
7 不同路径 II
leetcode 63. 不同路径 II
这题就是62的改版,所以复杂了很多,还是建议看代码随想录:动态规划——不同路径
动规五部曲:
- 确定dp数组(dp table)以及下标的含义
**dp[i] [j] :**表示从(0 ,0)出发,到(i, j) 有dp[i] [j]条不同的路径。
- 确定递推公式
递推公式和62.不同路径一样,dp[i] [j] = dp[i - 1] [j] + dp[i] [j - 1]。
但这里需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。
所以代码为:
if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
- dp数组如何初始化
因为从(0, 0)的位置到(i, 0)的路径只有一条,所以dp[i] [0]一定为1,dp[0] [j]也同理。
但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i] [0]应该还是初始值0。
如图:
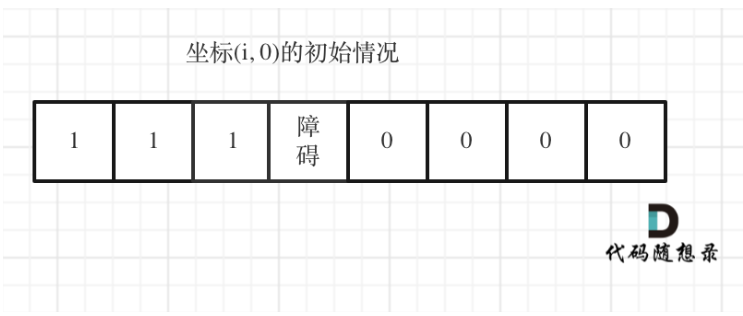
下标(0, j)的初始化情况同理。
所以本题初始化代码为:
int[][] dp = new int[m][n];
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {dp[i][0] = 1;
}
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {dp[0][j] = 1;
}
注意代码里for循环的终止条件,一旦遇到obstacleGrid[i] [0] == 1的情况就停止dp[i] [0]的赋值1的操作,dp[0] [j]同理
- 确定遍历顺序
从递归公式dp[i] [j] = dp [i - 1] [j] + dp[i] [j - 1] 中可以看出,一定是从左到右一层一层遍历,这样保证推导dp[i] [j]的时候,dp[i - 1] [j] 和 dp[i] [j - 1]一定是有数值。
代码如下:
for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;}
}
- 举例推导dp数组
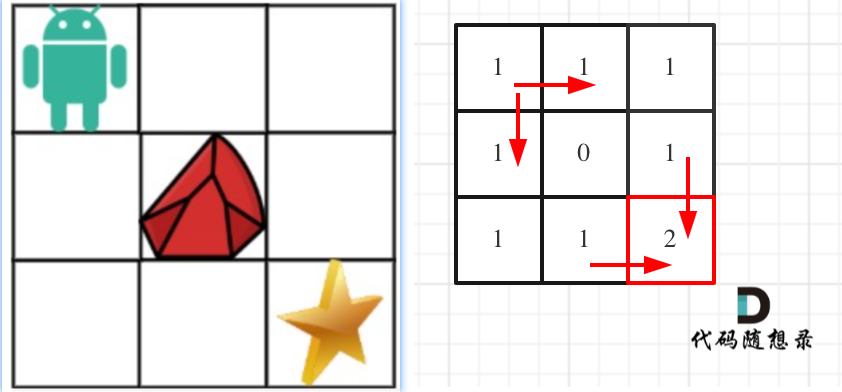
完整代码如下:
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] dp = new int[m][n];//如果在起点或终点出现了障碍,直接返回0if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {return 0;}for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {dp[i][0] = 1;}for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {dp[0][j] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;}}return dp[m - 1][n - 1];}
}
至于118,119我个人觉得并不合适使用动态规划的方式,所以就不写了,over~~
相关文章:

算法通关村第十九关——动态规划高频问题(白银)
算法通关村第十九关——动态规划高频问题(白银) 前言1 最少硬币数2 最长连续递增子序列3 最长递增子序列4 完全平方数5 跳跃游戏6 解码方法7 不同路径 II 前言 摘自:代码随想录 动态规划五部曲: 确定dp数组(dp tabl…...
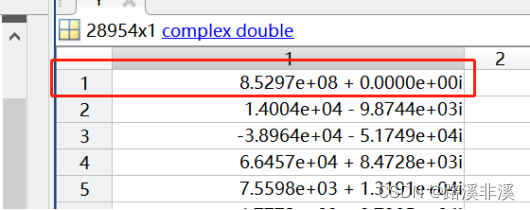
Matlab如何导入Excel数据并进行FFT变换
如果你发现某段信号里面有干扰,想要分析这段信号里面的频率成分,就可以使用matlab导入Excel数据后进行快速傅里叶变换(fft)。 先直接上使用方法,后面再补充理论知识。 可以通过串口将需要分析的数据发送到串口助手&a…...
华为mate60 上线 媒介盒子多家媒体报道
为什么你的品牌营销不见效?如何能推动品牌破圈?让媒介盒子给你一些启发。本期盒子要跟大家分享地新机上市,数码科技行业企业该如何做线上宣传。 HUAWEI Mate 60系列8月29日官宣发布,出色的拍照功能、强大的性能表现和持久的续航能…...

Java知识总结(持续更新)
一、JDK、JRE、JVM三者之间的关系? 1. **JDK (Java Development Kit)**: JDK 是 Java 开发工具包,它包含了用于开发 Java 应用程序的所有必要工具和库。这包括 Java 编译器(javac)、Java 核心类库、开发工具&#x…...

缓存技术:加速应用,提高用户体验
本文总结前期某个系统中使用到的缓存使用经验—仅此而已,效果还不错。 缓存技术在系统架构设计中扮演着至关重要的角色,它不仅可以显著提高系统的性能,还可以改善用户体验。在本文章中,我们将探讨不同类型的缓存、缓存失效以及缓存淘汰等关键概念,帮助在后期的架构设计中…...

MySQL中分区与分表的区别
MySQL中分区与分表的区别 一、分区与分表的区别 分区和分表是在处理大规模数据时的两种技术手段,尽管它们的目标都是提升系统的性能和数据管理的效率,但它们的实现方式和应用场景略有不同。 1. 分区 分区是将一个大表分割为多个更小的子表,…...
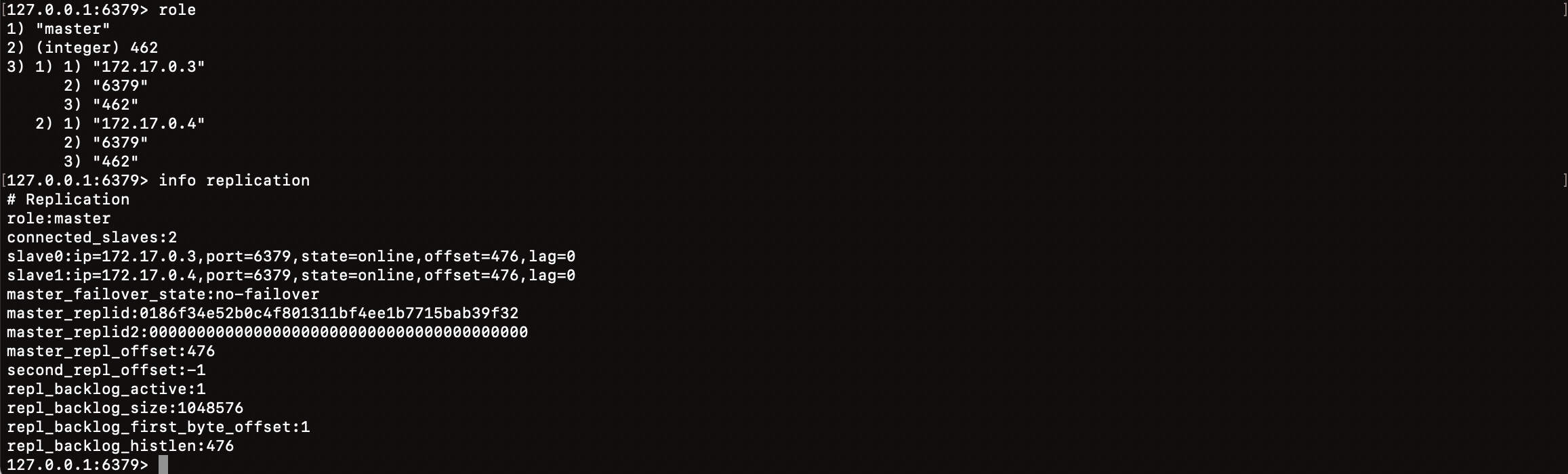
Redis主从复制集群的介绍及搭建
在现代的软件开发中,数据的可靠性和可用性是至关重要的。Redis,作为一个开源的、内存中的数据结构存储系统,以其出色的性能和灵活的数据结构,赢得了开发者们的广泛喜爱。而 Redis 的主从复制功能,更是为我们提供了一种…...

MAC M1芯片安装mounty读写移动硬盘中的文件
因为移动硬盘中的文件是微软公司NTFS格式,MAC只支持自己的APFS或者HFS,与微软的NTFS不兼容,所以需要第三方的软件来支持读写硬盘中的文件,经过一上午的折腾,最终选择安装mounty这个免费的第三方软件 工具网址连接&am…...

原生Js Canvas去除视频绿幕背景
Js去除视频背景 注: 这里的去除视频背景并不是对视频文件进行操作去除背景 如果需要对视频扣除背景并导出可以使用ffmpeg等库,这里仅作播放用所以采用这种方法 由于uniapp中的canvas经过封装,且 uniapp 的 drawImage 无法绘制视频帧画面&…...
每天10个小知识点)
Vue知识系列(1)每天10个小知识点
目录 系列文章目录知识点**1. Vue修饰符**的概念、作用、原理、特性、优点、缺点、区别、使用场景**2. 双向数据绑定**的概念、作用、原理、特性、优点、缺点、区别、使用场景**3. MVVM、MVC、MVP** 的概念、作用、原理、特性、优点、缺点、区别、使用场景**4. slot** 的概念、…...
聚合基本使用)
Elasticsearch(三)聚合基本使用
基础概念 bucket 数据分组,一些数据按照某个字段进行bucket划分,这个字段值相同的数据放到一个bucket中。可以理解成Java中的Map<String, List>结构,类似于Mysql中的group by后的查询结果。 metric: 对一个数据分组执行…...

单片机C语言实例:14、音频输出
一、喇叭发声原理 程序实例1: #include<reg52.h> //包含头文件,一般情况不需要改动,头文件包含特殊功能寄存器的定义sbit SPK P1^2; //定义喇叭端口 /*------------------------------------------------函数声明 --------------…...

docker 和 podman的区别
Podman 和 Docker 都是用于容器化应用程序的工具,它们在很多方面非常相似,但也有一些关键区别: 1. 架构和权限: - Docker:Docker 使用守护进程(dockerd)来管理容器,它需要在操作…...
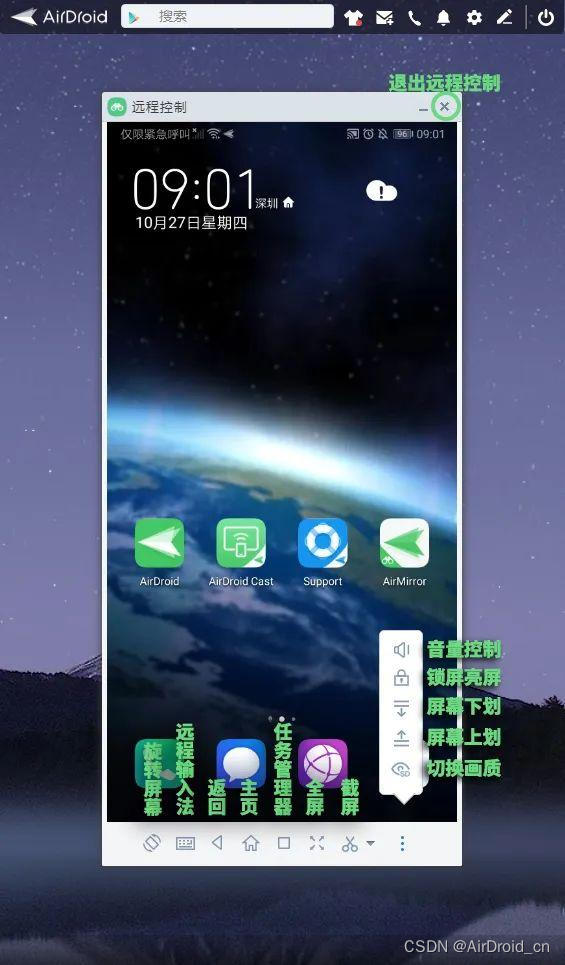
苹果手机远程控制安卓手机,为什么不能发起控制?
这位用户想要用iOS设备远程控制安卓设备,在被控端安装好AirDroid之后,就在控制端的苹果手机上也安装了AirDroid,然而打开控制端的软件,却没有在手机界面上看到【远程控制】按钮,于是提出了以上疑问。 解答 想要让iOS设…...

Gradle 配置国内镜像
我们在使用gradle构建项目的时候,每当需要build或者刷新依赖的时候,由于gradle需要从服务器下载各种依赖包,速度非常慢,根本原因是由于gradle服务器在国外,而国内有些一些大厂和高校(比如阿里,华为…...

Spring AOP使用指南: 强大的面向切面编程技术
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

Spring Boot集成Elasticsearch实战
文章目录 一、简介二、安装与配置Elasticsearch三、集成Spring Boot与Elasticsearch1. 添加依赖与配置文件2. 创建Elasticsearch数据模型3. 定义Elasticsearch仓库接口4. 实现Elasticsearch数据操作 四、基本查询与索引操作1. 插入与更新数据2. 删除数据与索引3. 条件查询与分页…...

【python零基础入门学习】python基础篇之文件对象open、模块以及函数的使用(三)
本站以分享各种运维经验和运维所需要的技能为主 《python》:python零基础入门学习 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8》暂未更新 《docker学习》暂未更新 《ceph学习》ceph日常问题解…...
【JavaEE】_CSS常用属性值
目录 1. 字体属性 1.1 设置字体家族 font-family 1.2 设置字体大小 font-size 1.3 设置字体粗细 font-weight 1.4 设置字体倾斜 font-style 2. 文本属性 2.1 设置文本颜色 color 2.2 文本对齐 text-align 2.3 文本装饰 text-decoration 2.4 文本缩进 text-indent 2.…...
vue组件库开发,webpack打包,发布npm
做一个像elment-ui一样的vue组件库 那多好啊!这是我前几年就想做的 但webpack真的太难用,也许是我功力不够 今天看到一个视频,早上6-13点,终于实现了,呜呜 感谢视频的分享-来龙去脉-大家可以看这个视频:htt…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...
