算法 数据结构 斐波那契数列 递归实现斐波那契数列 斐波那契递归的优化 斐波那契数列递归求解 多路递归实现 斐波那契算法系列 数据结构(十一)
1. 什么是斐波那契数列:
-
之前的例子是每个递归函数只包含一个自身的调用,这称之为 single recursion
-
如果每个递归函数例包含多个自身调用,称之为 multi recursion
递推关系
下面的表格列出了数列的前几项
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 |
多路递归斐波那契代码实现1:
package com.nami.algorithm.study.day07;/*** beyond u self and trust u self.** @Author: lbc* @Date: 2023-09-06 9:29* @email: 594599620@qq.com* @Description: keep coding*/
public class Fibonacci {/*** 出现问题的,计算 n= 88 根本算不出来。多路递归一直在循环里面了。出不来 --!* @param n* @return*/public static int calculate(int n) {if (n == 0) {return 0;}if (n == 1) {return 1;}int f1 = calculate(n - 1);int f2 = calculate(n - 2);return f1 + f2;}public static void main(String[] args) {// 时间复杂度: 2*f(n+1) -1// E(1.618N次方)System.out.println(calculate(88));}}
非递归实现2 --- LeetCode 70. 爬楼梯 计算爬楼梯共计多少种方法可达_不努力就种地~的博客-CSDN博客
之前写的爬楼梯解决方案:
public static int climbStairs(int n) {int[] dp = new int[n + 1];dp[0] = 1;dp[1] = 1;for(int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}这种方法直接用数组去存储前面计算的值,不用重复计算。没有出现上面n=88出现的计算缓慢问题
递归优化方案:
使用数组,存储之前计算的数据,减少计算次数。妙哉
package com.nami.algorithm.study.day07;import java.util.Arrays;/*** beyond u self and trust u self.** @Author: lbc* @Date: 2023-09-06 9:29* @email: 594599620@qq.com* @Description: keep coding*/
public class FastFibonacci {/*** 出现问题的,计算 n= 100000* 出现异常 StackOverflowError* 方法层级太深,会导致栈溢出** @param n* @return*/public static int calculate(int n) {// 初始化缓存// ==>记忆法// 空间换时间int[] cache = new int[n + 1];// 填充-1 标识未该值为计算Arrays.fill(cache, -1);cache[0] = 0;cache[1] = 1;return fibonacci(n, cache);}/*** 时间复杂度: O(n)* 增加额外空间成本** @param n* @param cache* @return*/private static int fibonacci(int n, int[] cache) {if (cache[n] != -1) {return cache[n];}int f1 = fibonacci(n - 1, cache);int f2 = fibonacci(n - 2, cache);cache[n] = f1 + f2;return cache[n];}public static void main(String[] args) {// n=88也有问题,出现-值// -2092787285System.out.println(calculate(88));}}
使用数组进行优化,也有一个问题,数组只有n-1, n-2两个值有用。对于计算之后,存储前面n-3的值没有了意义;
优化2 ==>尾递归:
尾递归(防止栈溢出) + 只取n-1, n-2的值流转
package com.nami.algorithm.study.day07;/*** 尾递归 斐波那契数列* beyond u self and trust u self.** @Author: lbc* @Date: 2023-09-06 9:29* @email: 594599620@qq.com* @Description: keep coding*/
public class TailRecFibonacci {/*** @param n* @return*/public static int calculate(int n) {return fibonacci(n, 0, 1);}private static int fibonacci(int n, int first, int second) {if (n == 0) {return first;}if (n == 1) {return second;}return fibonacci(n - 1, second, first + second);}public static void main(String[] args) {// n=47,出现-值// -1323752223// 18 3631 1903 + 11 3490 3170// n= 46 + n=45// int 最大值 21 4748 3647System.out.println(calculate(46));}}
为什么斐波那契数列会出现负值?
当n=88时,结果等于负数。排查发现:当n=46是正常的,n=47时,前面两个值的相加已经超过了int最大值int.max_value= 21 4748 3647 所以出现负数
如何根本上解决爆栈问题:
递归转for or while循环解决问题。
相关文章:
算法 数据结构 斐波那契数列 递归实现斐波那契数列 斐波那契递归的优化 斐波那契数列递归求解 多路递归实现 斐波那契算法系列 数据结构(十一)
1. 什么是斐波那契数列: 之前的例子是每个递归函数只包含一个自身的调用,这称之为 single recursion 如果每个递归函数例包含多个自身调用,称之为 multi recursion 递推关系 下面的表格列出了数列的前几项 F0F1F2F3F4F5F6F7F8F9F10F11F12…...
【面试经典150 | 双指针】两数之和
文章目录 写在前面Tag题目来源题目解读解题思路方法一:暴力枚举方法二:哈希表方法三:二分法方法四:双指针 知识回顾写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢…...

桥接模式简介
概念: 桥接模式是一种结构型设计模式,它将抽象和实现分离,使它们可以独立地变化。通过使用桥接模式,可以将一个类的抽象部分与其具体实现部分解耦,并且可以在运行时动态地选择不同的实现。 特点: 将抽象…...
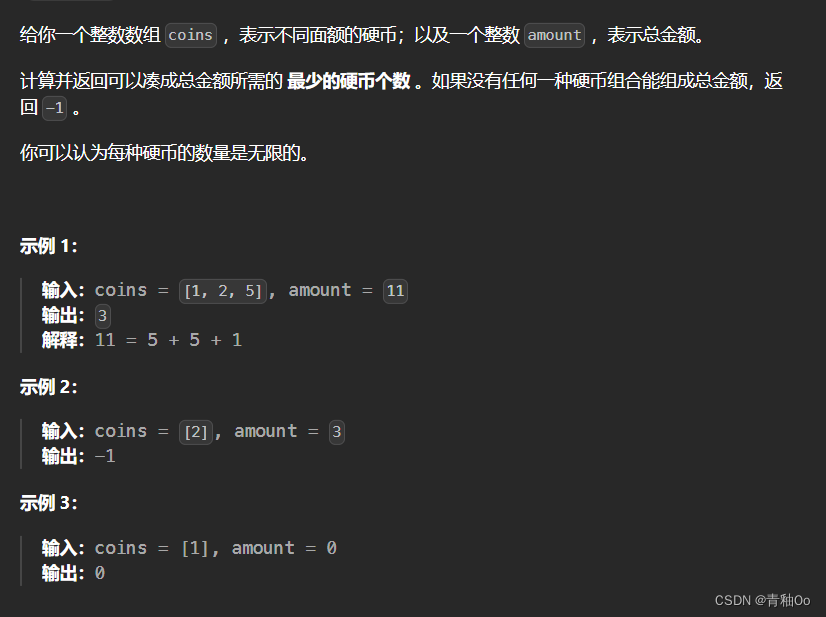
零钱兑换00
题目链接 零钱兑换 题目描述 注意点 如果没有任何一种硬币组合能组成总金额,返回 -1可以认为每种硬币的数量是无限的 解答思路 动态规划从总金额1开始推出目标金额所需的最少硬币个数,任意某个金额所需的最少硬币个数可以由当前金额减去每种面额的硬…...
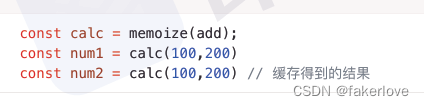
JavaScipt中如何实现函数缓存?函数缓存有哪些场景?
1、函数缓存是什么? 函数缓存就是将函数运行的结果进行缓存。本质上就是用空间(缓存存储)换时间(计算过程) 常用于缓存数据计算结果和缓存对象。 缓存只是一个临时的数据存储,它保存数据,以便将…...
android studio的Android Drawable Preview
Android Drawable Preview 应用后,如下图: 再也不用一个一个点开去看了 其他学习资料: 1、付费专栏《Android kotlin入门到进阶系列讲解》:https://blog.csdn.net/qq_35091074/category_11036895.html 2、免费专栏《Android kot…...
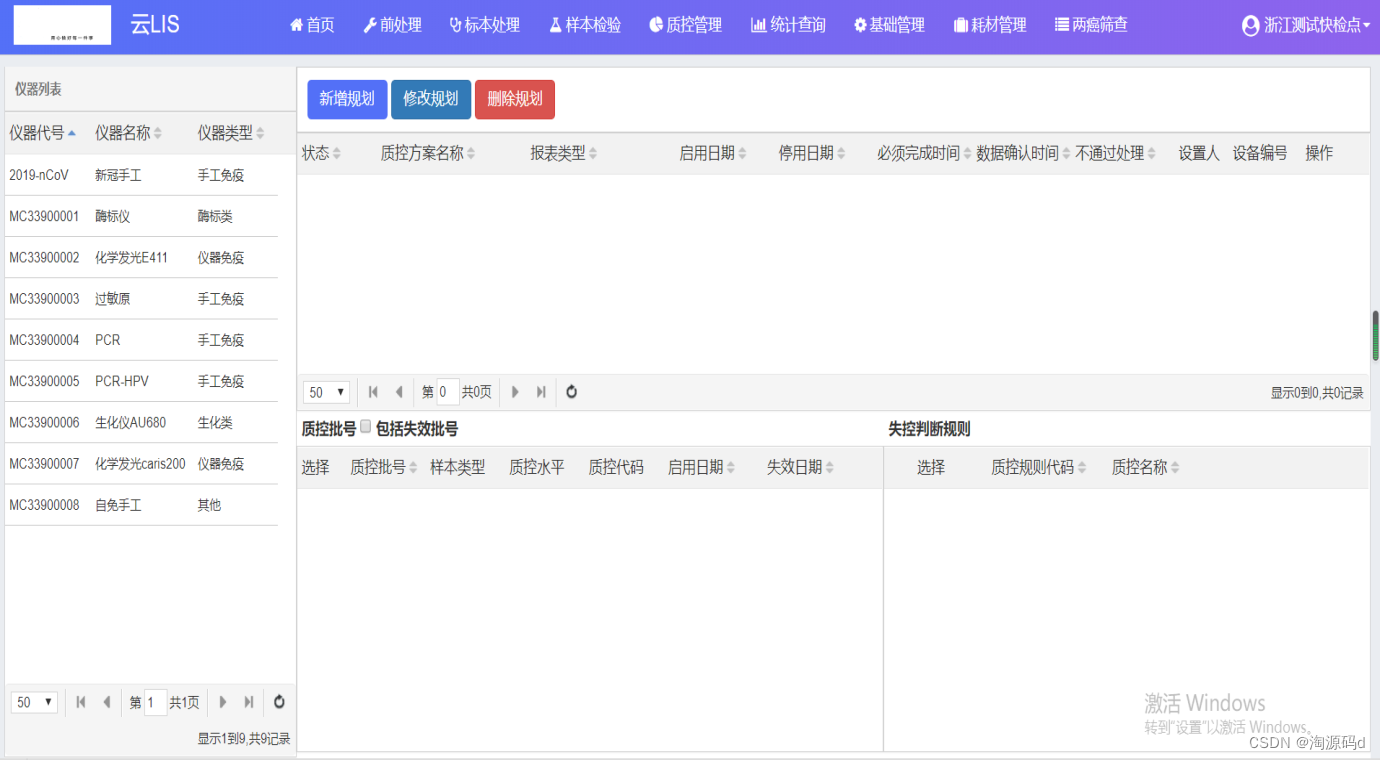
基于云计算的区域LIS系统系统源码
在医疗机构内部,院内实验室主要负责本院临床科室的检验,院内LIS系统必须满足实验室日常的标本处理入库、仪器联机、检验结果处理、报告打印、报告发布、检验信息统计、检验信息报告发布、标本流程、外部医疗机构检验报告调阅等工作。 在医疗机构间&#…...

VR农学虚拟仿真情景实训教学演示
首先,VR农学虚拟仿真情景实训教学提供了更为真实的实践环境。传统的农学实训往往受制于时间、空间和资源的限制,学生只能通过观察或简单的模拟来学习农业知识和技能。而借助虚拟现实技术,学生可以进入虚拟农场,与各种农作物、工具…...
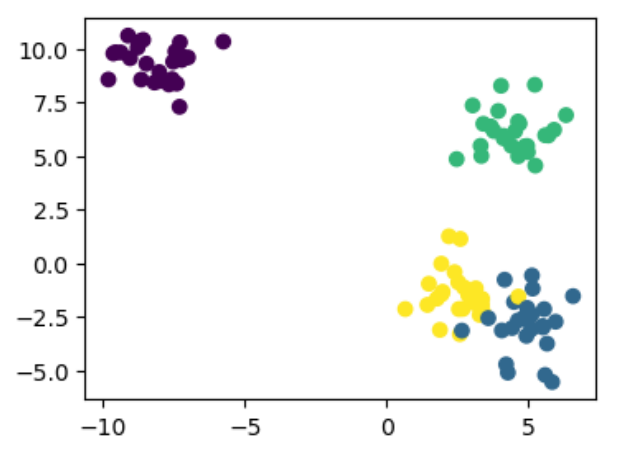
sklearn中make_blobs方法:聚类数据生成器
sklearn中make_blobs()方法参数: n_samples:表示数据样本点个数,默认值100 n_features:是每个样本的特征(或属性)数,也表示数据的维度,默认值是2。默认为 2 维数据,测试选取 2 维数据也方便进行可视化展示…...

Win11自带微软输入法怎么输入π及其他希腊字母
如果用搜狗等第三方输入法的话就没有这些问题了,各种符号很方便。 自带的输入法输入 pi 和 pai 都不能正常输入 π \pi π 参考文章 https://www.cnblogs.com/qq-757617012/p/14078133.html 如果用自带的输入法可以采用以下方式 输入uuxl xl表示“希腊”&#x…...

关于MyBatisPlus框架下出现xml里面定义的方法无法被正确识别以及提示调用mysql存储过程时参数无效的问题
第一个问题:xml里面明明定义了方法A,但是通过IService接口调用A的时候,总提示无法将接口中定义的函数绑定到xml中的同名方法中(“Invalid bound statement (not found): com.aircas.sqlservice.mapper.SysTempIndexMapper.getRemo…...

vscode路径别名文件跳转解决办法
第一步:下载 1.在jsconfig.json中配置: {"compilerOptions": {"target": "es5","module": "esnext","baseUrl": "./","moduleResolution": "node","p…...

layui 富文本编辑器layedit 以及 图片转base64前端页面显示
js var index layui.layedit.build(noticeInformationContent, {area: [500px, 400px],uploadImage: {url: NI/uploadconimage //接口url, type: POST //默认post},hideTool: [image]});layui.form.verify({content: function (val) {layui.layedit.sync(index);var content …...

服务器给前端实时推送数据轻量化解决方案eventSource+Springboot
一、前端代码 body代码 <div id"result"></div>js代码 $(function(){if(typeof(EventSource) ! "undefined"){var source new EventSource("/demo/getTime");source.onmessage function(event) {console.log(event.data);$(&qu…...
数据结构与算法:数据结构基础
目录 数组 定义 形式 顺序存储 基本操作 读取元素 更新元素 插入元素 删除元素 扩容 初始化 时机 步骤 优劣势 链表 定义 单向链表 特点 双向链表 随机存储 基本操作 查找节点 更新节点 插入节点 删除元素 数组VS链表 栈与队列 栈 定义 基本操作…...

virtualbox虚拟机中安装FreeDOS系统和DJGPP编译环境
一、安装FreeDOS系统 1、从官网下载FreeDOS系统镜像,下载的压缩包中包含两个文件:后缀为.iso和.img的镜像 下载页面 http://www.freedos.org/download/ 直接下载链接 https://www.ibiblio.org/pub/micro/pc-stuff/freedos/files/distributions/1.…...
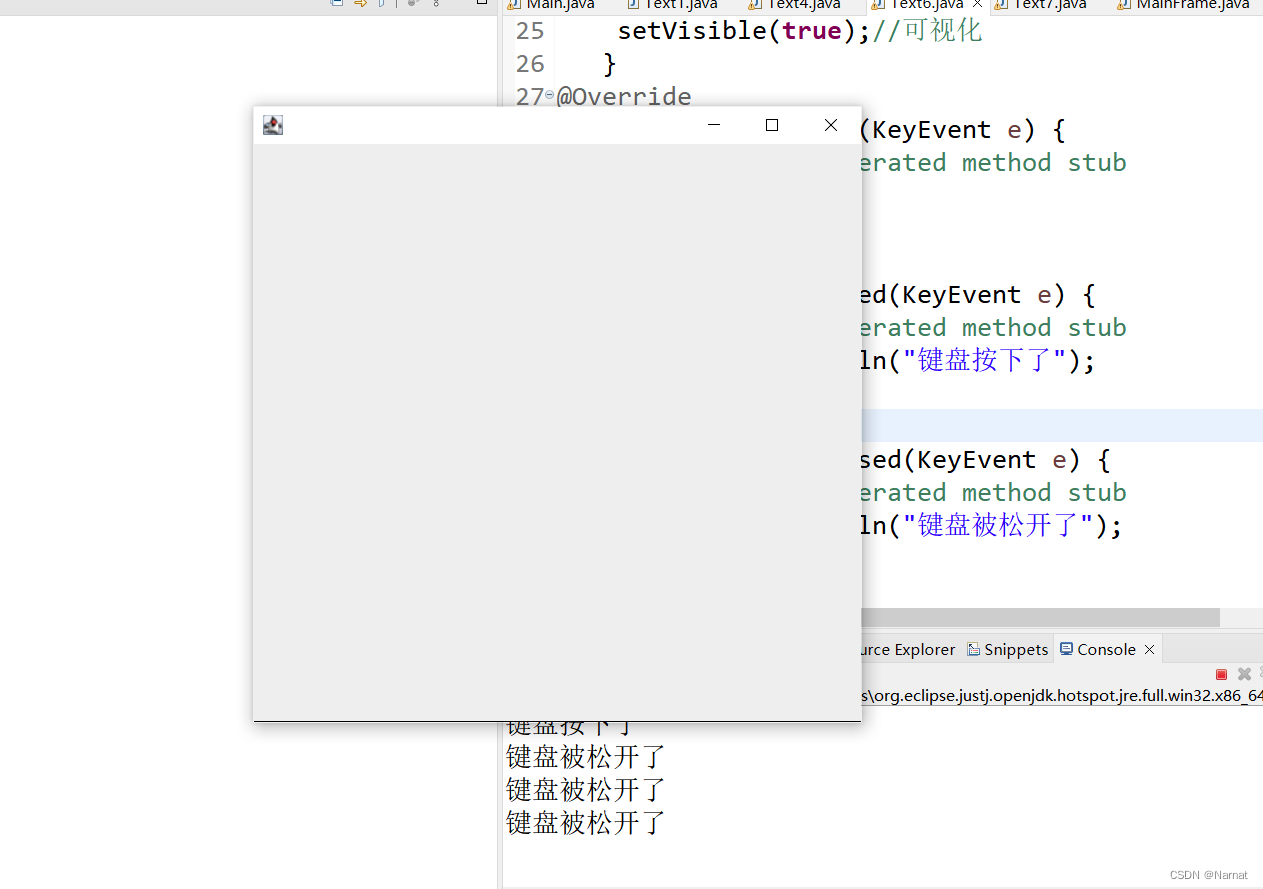
JAVASE事件监听
代码: import java.awt.event.ActionEvent; import java.awt.event.ActionListener; import java.util.ArrayList; import java.util.HashMap; import java.util.List; import java.util.Map; import java.util.Scanner;import javax.swing.JButton; import javax.…...
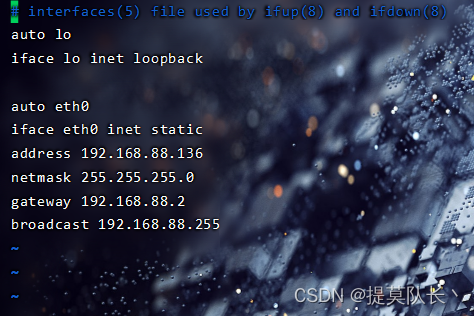
ubuntu14.04改静态ip
现在可能已经用ubuntu14.04的人已经不多了,这里讲一下Ubuntu14.04怎么改静态ip 第一步:输入ifconfig查看ip和子网掩码 第二步:输入route -n查看网关 上面ip是192.168.88.136,子网掩码是255.255.255.0,网关是192.168.…...
“文件的上传与下载:实现与优化“
目录 引言1.文件的上传2.文件的下载3. JRebel安装使用4. 文件批量上传总结 引言 在开发过程中,文件的上传与下载是常见的需求。本篇博客将以CSND为例,介绍文件上传与下载的常见方式,以及如何通过优化提升性能和用户体验。 1.文件的上传 使…...

uboot顶层Makefile前期所做工作说明三
一. uboot顶层 Makefile文件 uboot顶层 Makefile,就是 uboot源码工程的根目录下的 Makefile文件。 本文继续对 uboot顶层 Makefile的前期准备工作进行介绍。续上一篇文章内容的学习,如下: uboot顶层Makefile前期所做工作说明二_凌肖战的博…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
