地图结构 | 图解占据栅格地图原理(附Matlab建图实验)
目录
- 0 专栏介绍
- 1 栅格地图
- 1.1 应用场景
- 1.2 基本概念
- 2 占据栅格地图
- 2.1 更新模型
- 2.2 截断策略
- 3 仿真实现
- 3.1 算法流程
- 3.2 Matlab实现
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 栅格地图
1.1 应用场景

栅格地图(grid map)是在机器人和自动化领域中广泛使用的一种地图表示方法。它将环境划分为规则的网格单元,并在每个单元中存储关于该区域的信息。每个单元可以表示空闲、障碍物、未知区域或其他地图属性。
栅格地图最主要的应用是服务于机器人导航中的路径规划和避障。机器人可以利用栅格地图中的障碍物信息来规划安全的路径,并避开可能的碰撞或危险区域。同时,栅格地图也是SLAM算法中常用的地图表示方式之一。通过与传感器数据融合,机器人能够同时进行自身位置估计和地图构建。
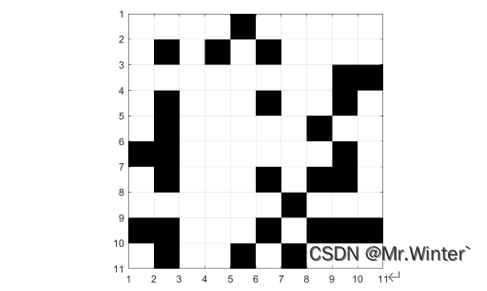
总之,栅格地图是一种简单且直观的地图表示方法,它可以提供对环境的可视化和语义信息,并为机器人的感知、规划和决策提供基础。然而,栅格地图也存在分辨率、存储消耗和精度等方面的限制,在实际应用中需要权衡和优化。
1.2 基本概念
栅格地图的基本概念总结如下
-
邻域模式
栅格地图中常用的邻域模式有8邻域法、24邻域法和48邻域法,如下所示
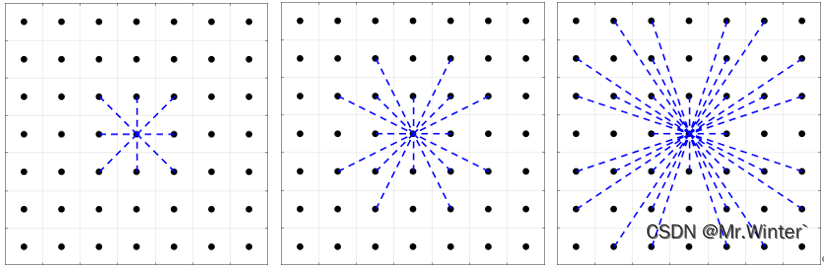
-
栅格示数
栅格地图中每个栅格都被赋予栅格示数,其指明了该栅格在全局环境中表达的语义。例如0表示无障碍的自由栅格,1表示障碍物
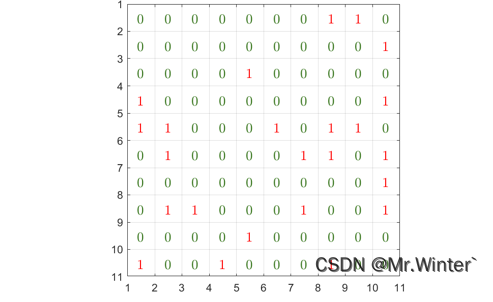
-
栅格坐标
栅格地图可视为离散直角坐标系,其中可用有序二元组 ( i , j ) (i,j) (i,j)定位栅格 -
栅格序号
栅格按照行列顺序依次进行的编号称为栅格序号,由于栅格序号是一维线性的,因此可以加速信息处理与运算
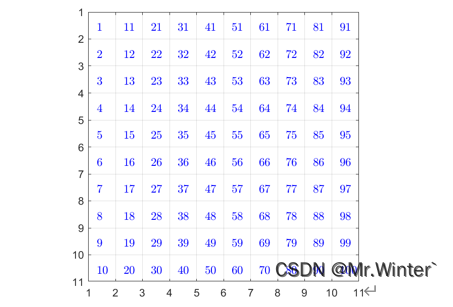
-
栅格粒度
栅格对应物理世界的比例系数称为栅格粒度,栅格粒度越小,环境分辨率越大,对环境的刻画越具体、丰富。但相应地,存储地图所占的内存、处理地图耗费的时间越多
2 占据栅格地图
在工程上,通常使用占据法构建占据栅格地图(Occupancy Grid Map)。考虑到构建栅格地图使用的激光雷达存在噪声,即在相同条件下对障碍物的相对距离探测可能有误差,因此引入概率定义栅格状态:对于地图中的栅格 s s s, P ( s = 1 ) P\left( s=1 \right) P(s=1)表示栅格被占据的概率; P ( s = 0 ) = 1 − P ( s = 1 ) P\left( s=0 \right) =1-P\left( s=1 \right) P(s=0)=1−P(s=1)表示栅格自由的概率。实际应用时,使用一种更紧凑的表达
o d d ( s ) = P ( s = 1 ) P ( s = 0 ) \mathrm{odd}\left( s \right) =\frac{P\left( s=1 \right)}{P\left( s=0 \right)} odd(s)=P(s=0)P(s=1)
2.1 更新模型
构建地图的问题可形式化为:已知机器人激光传感器的观测序列 ,更新地图中栅格的后验概率 ,根据贝叶斯公式和马尔科夫链可得
P ( s ∣ z 1 : t ) = P ( z t ∣ s , z 1 : t − 1 ) P ( s ∣ z 1 : t − 1 ) P ( z t ∣ z 1 : t − 1 ) = P ( z t ∣ s ) ⏞ M a r k o v P ( s ∣ z 1 : t − 1 ) P ( z t ∣ z 1 : t − 1 ) = P ( s ∣ z t ) P ( z t ) ⏞ B a y e s P ( s ∣ z 1 : t − 1 ) P ( s ) P ( z t ∣ z 1 : t − 1 ) \begin{aligned}P\left( s|z_{1:t} \right) &=\frac{P\left( z_t|s,z_{1:t-1} \right) P\left( s|z_{1:t-1} \right)}{P\left( z_t|z_{1:t-1} \right)}\\\,\, & =\frac{{ \overset{\mathrm{Markov}}{\overbrace{P\left( z_t|s \right) }}}P\left( s|z_{1:t-1} \right)}{P\left( z_t|z_{1:t-1} \right)}\\&=\frac{{ \overset{\mathrm{Bayes}}{\overbrace{P\left( s|z_t \right) P\left( z_t \right) }}}P\left( s|z_{1:t-1} \right)}{{ P\left( s \right) }P\left( z_t|z_{1:t-1} \right)}\end{aligned} P(s∣z1:t)=P(zt∣z1:t−1)P(zt∣s,z1:t−1)P(s∣z1:t−1)=P(zt∣z1:t−1)P(zt∣s) MarkovP(s∣z1:t−1)=P(s)P(zt∣z1:t−1)P(s∣zt)P(zt) BayesP(s∣z1:t−1)
计算后验概率优势比
P ( s = 1 ∣ z 1 : t ) P ( s = 0 ∣ z 1 : t ) = P ( s = 1 ∣ z t ) P ( s = 0 ∣ z t ) ⋅ P ( s = 1 ∣ z 1 : t − 1 ) P ( s = 0 ∣ z 1 : t − 1 ) ⋅ P ( s = 0 ) P ( s = 1 ) \frac{P\left( s=1|z_{1:t} \right)}{P\left( s=0|z_{1:t} \right)}=\frac{P\left( s=1|z_t \right)}{P\left( s=0|z_t \right)}\cdot \frac{P\left( s=1|z_{1:t-1} \right)}{P\left( s=0|z_{1:t-1} \right)}\cdot \frac{P\left( s=0 \right)}{P\left( s=1 \right)} P(s=0∣z1:t)P(s=1∣z1:t)=P(s=0∣zt)P(s=1∣zt)⋅P(s=0∣z1:t−1)P(s=1∣z1:t−1)⋅P(s=1)P(s=0)
一般令先验概率 P ( s = 0 ) = P ( s = 1 ) = 0.5 P\left( s=0 \right) =P\left( s=1 \right) =0.5 P(s=0)=P(s=1)=0.5,引入Logistic变换
L ( p ) = log [ p / ( 1 − p ) ] L\left( p \right) =\log \left[ {{p}/{\left( 1-p \right)}} \right] L(p)=log[p/(1−p)]
则
L ( s ∣ z 1 : t ) = L ( s ∣ z t ) + L ( s ∣ z 1 : t − 1 ) L\left( s|z_{1:t} \right) =L\left( s|z_t \right) +L\left( s|z_{1:t-1} \right) L(s∣z1:t)=L(s∣zt)+L(s∣z1:t−1)
称为栅格状态的更新模型。更新模型中与新测量值 z t z_t zt有关的项是 L ( s ∣ z t ) L\left( s|z_t \right) L(s∣zt),由于激光雷达的测量值只有两种情况,因此定义
{ l o o c c u : L ( s ∣ z t = 1 ) l o f r e e : L ( s ∣ z t = 0 ) \begin{cases} \mathrm{looccu}: L\left( s|z_t=1 \right)\\ \mathrm{lofree}: L\left( s|z_t=0 \right)\\\end{cases} {looccu:L(s∣zt=1)lofree:L(s∣zt=0)
必须指出, l o o c c u \mathrm{looccu} looccu与 l o f r e e \mathrm{lofree} lofree表达了在获得感知数据的情况下栅格真实状态的概率,这是与传感器性能有关的常数。传感器性能越好,测量结果越接近真实值, l o o c c u \mathrm{looccu} looccu越大 l o f r e e \mathrm{lofree} lofree越小。一般地,可以设定 l o o c c u = 0.9 \mathrm{looccu}=0.9 looccu=0.9、 l o f r e e = − 0.7 \mathrm{lofree}=-0.7 lofree=−0.7
2.2 截断策略
从更新模型可以看出, L ( s ∣ z 1 : t ) L\left( s|z_{1:t} \right) L(s∣z1:t)是对历史观测序列的整合。换言之,若假设 ∣ l o o c c u ∣ = ∣ l o f r e e ∣ \left| \mathrm{looccu} \right|=\left| \mathrm{lofree} \right| ∣looccu∣=∣lofree∣,则当一个栅格被观察到 k k k次自由状态后,必须再被观察到至少 k k k次占据状态,才有可能被设置为占据栅格。这导致实际应用时,动态环境中的地图可能无法被快速更新。
为了建图的适应性,采用截断策略,定义概率上下限来限制改变栅格状态所需的更新次数,代价是概率在0-1区间内不再完备,靠近边界的概率丢失
L ( s ∣ z 1 : t ) = max { min { L ( s ∣ z t ) + L ( s ∣ z 1 : t − 1 ) , L max } , L min } L\left( s|z_{1:t} \right) =\max \left\{ \min \left\{ L\left( s|z_t \right) +L\left( s|z_{1:t-1} \right) , L_{\max} \right\} , L_{\min} \right\} L(s∣z1:t)=max{min{L(s∣zt)+L(s∣z1:t−1),Lmax},Lmin}
3 仿真实现
3.1 算法流程
算法流程如下所示

其中关于Bresenham视线法原理,请参考路径规划 | 图解Theta*算法(附ROS C++/Python/Matlab仿真)
3.2 Matlab实现
核心代码如下所示
for i = 1:N x = scan_pose(1, i);y = scan_pose(2, i);theta = scan_pose(3, i);robot_pos = [ceil(x * resolution) + origin(1), ceil(y * resolution) + origin(2)];% Find grids hit by the rays (in the gird map coordinate)rays = scan_ranges(:, i);x_occ = rays .* cos(scan_angles + theta) + x;y_occ = -rays .* sin(scan_angles + theta) + y;occ_pos = [ceil(x_occ * resolution) + origin(1), ceil(y_occ * resolution) + origin(2)];% Find occupied-measurement cells and free-measurement cellsocc_id = sub2ind(size(grid_map), occ_pos(:, 2), occ_pos(:, 1));free = [];for j = 1:scans_num[ix_free, iy_free] = bresenham(robot_pos, occ_pos(j, :)); free = [free; iy_free, ix_free];endfree_id = sub2ind(size(grid_map), free(:, 1), free(:, 2));% Update the log-oddsgrid_map(occ_id) = grid_map(occ_id) + lo_occ;grid_map(free_id) = grid_map(free_id) - lo_free;% Saturate the log-odd valuesgrid_map(grid_map > lo_max) = lo_max;grid_map(grid_map < lo_min) = lo_min;
end

完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

地图结构 | 图解占据栅格地图原理(附Matlab建图实验)
目录 0 专栏介绍1 栅格地图1.1 应用场景1.2 基本概念 2 占据栅格地图2.1 更新模型2.2 截断策略 3 仿真实现3.1 算法流程3.2 Matlab实现 0 专栏介绍 🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索…...
element-plus点击菜单栏全部展开问题解决
这是由子菜单项的index属性引起的,子菜单项的index属性添加相同的值时就会出现这种情况。所以为每个子菜单项添加不同的index属性值就可解决。...

React 简便获取经纬度
以下是关于React获取定位经纬度的代码解释: import React, { useEffect, useState } from react;const LocationComponent () > {const [latitude, setLatitude] useState(null);const [longitude, setLongitude] useState(null);useEffect(() > {navigat…...
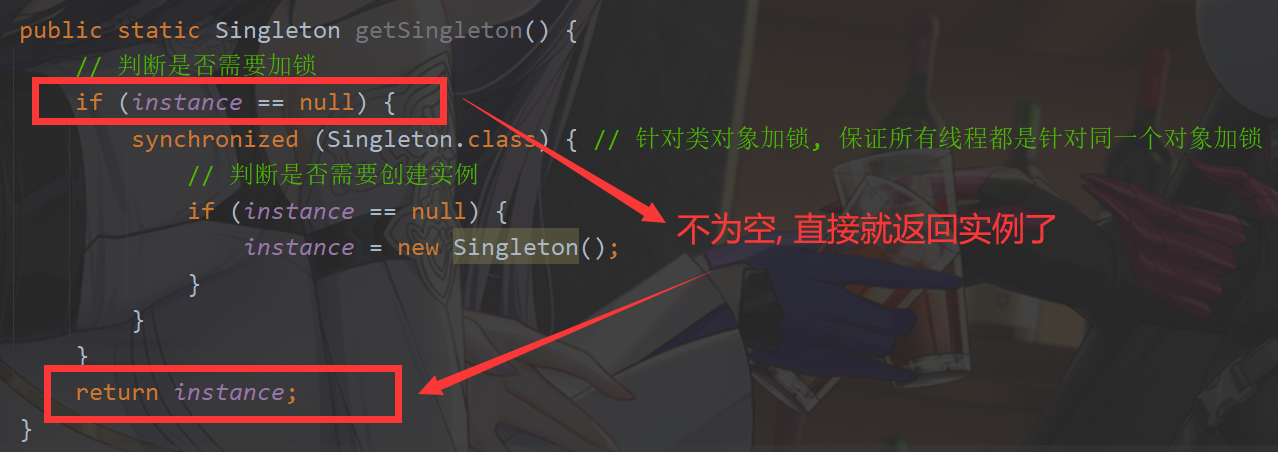
【多线程】线程安全的单例模式
线程安全的单例模式 饿汉模式懒汉模式单线程版多线程版多线程版(改进) 单例模式能保证某个类在程序中只存在 唯一 一份实例, 而不会创建出多个实例,从而节约了资源并实现数据共享。 比如 JDBC 中的 DataSource 实例就只需要一个. 单例模式具体的实现方式, 分成 “饿…...
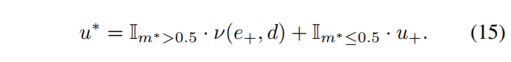
Competitive Collaboration 论文阅读
论文信息 题目:Competitive Collaboration: Joint Unsupervised Learning of Depth, Camera Motion, Optical Flow and Motion Segmentation 作者:Anurag Ranjan, Varun Jampani, Lukas Balles 来源:CVPR 时间&#x…...
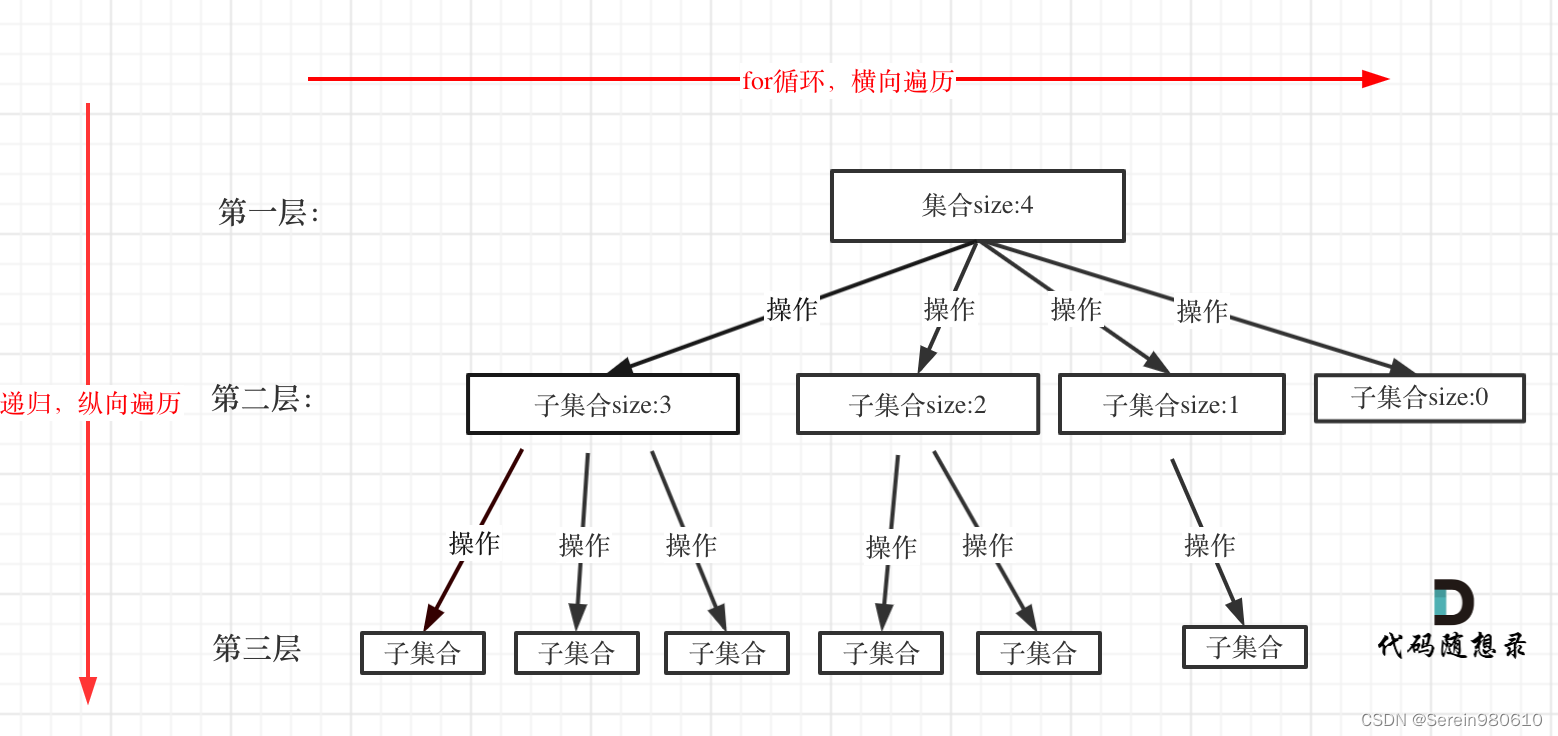
非科班菜鸡算法学习记录 | 代码随想录算法训练营完结!
这俩月终于结束了233333,之后就是反复复习和背八股了吧,然后整整项目春招再投投投,感觉大部分题都有思路了但是做过的题也会没思路,还是要复习 总结 数组: 双指针用的很多,一般一个指向遍历位置࿰…...

C语言实现三字棋
实现以下: 1游戏不退出,继续玩下一把(循环) 2应用多文件的形式完成 test.c. --测试游戏 game.c -游戏函数的实现 game.h -游戏函数的声明 (2)游戏再走的过程中要进行数据的存储,可以使用3*3的二维数组 char bor…...

【LeetCode】35.复杂链表的复制
题目 请实现 copyRandomList 函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。 示例 1: 输入:head [[7,null],[13,0],[11,4]…...
)
代码大全阅读随笔(五)
数据初始化要点: 数据初始化过程很容易出错,所以请使用本章介绍的方法,来初始化数据,从而避免由于非预期的初始化值而造成的错误。 最小化变量作用域。 使用相同的变量的语句尽可能的集中在一起。 早期绑定会减少灵活性࿰…...

No1.详解【2023年全国大学生数学建模竞赛】C题——蔬菜类商品的自动定价与补货决策(代码 + 详细输出 + 数据集代码 下载)
时间告诉你什么叫衰老,回忆告诉你什么叫幼稚。不要总在过去的回忆里纠缠,昨天的太阳,晒不干今天的衣裳。 🎯作者主页: 追光者♂🔥 🌸个人简介: 💖[1] 计算机专业硕士研究生💖 🌿[2] 2023年城市之星领跑者TOP1(哈尔滨)🌿 🌟[3] 2022年度博客…...

有什么好用的电容笔?apple pencil替代品推荐
近年来,电容笔越来越成为人们日常生活中常见的数码产品之一。电容笔的便捷性得到了消费者的认可。它逐渐取代无纸化书写。那么到底电容笔哪个品牌好呢,电容笔哪一款最好用呢,今天小编给大家总结几款市面好用的电容笔,让我们一起来…...

什么是回调函数?写出一个示例?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 回调函数⭐ 示例⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为那些对Web开发感兴趣、刚刚踏入前…...

深度学习在医疗保健领域的应用:从图像识别到疾病预测
文章目录 深度学习在医学影像识别中的应用1. 癌症检测2. 病理学图像分析3. 医学图像分割 深度学习在疾病预测中的应用1. 疾病风险预测2. 疾病诊断辅助3. 药物研发 深度学习在个性化治疗中的应用1. 基因组学分析2. 临床数据集成 深度学习在医疗保健中的挑战和未来数据隐私和安全…...

SpringBoot实现自定义environment中的value加密
environment中的value为什么要加密? 未经过加密的配置文件,密码均是采用明文密码,很容易导致信息泄露。 SpringBoot environment中的value加密代码如下 package com.xxx.core.encryption;import com.google.common.collect.Maps; import lomb…...

celery的用法--任务调度
在Celery中,任务(Task)是执行特定操作的基本单元。任务可以异步执行,可以带有参数,可以返回结果,可以链式调用,还可以设置任务优先级、超时等属性。 1.定义任务: 使用app.task装饰器…...

MyBatis-Plus学习笔记总结
一、查询 构造器分为QueryWrapper和LambdaQueryWrapper 创建实体类User package com.system.mybatisplus.model;import com.baomidou.mybatisplus.annotation.IdType; import com.baomidou.mybatisplus.annotation.TableField; import com.baomidou.mybatisplus.annotation.…...

How Language Model Hallucinations Can Snowball
本文是LLM系列文章,针对《How Language Model Hallucinations Can Snowball》的翻译。 语言模型幻觉是如何产生雪球的 摘要1 引言2 为什么我们期待幻觉像滚雪球一样越滚越大?3 实验4 我们能防止雪球幻觉吗?5 相关工作6 结论局限性 摘要 在实…...
autojs修改顶部标题栏颜色
顶部标题栏的名字是statusBarColor 不是toolbar。难怪我搜索半天搜不到 修改之后变成这样了 代码如下: "ui"; importClass(android.view.View); importClass(android.graphics.Color); ui.statusBarColor(Color.parseColor("#ffffff")); ui.…...
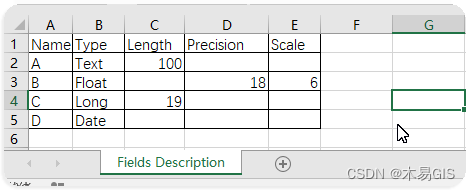
arppy gis 读取text 并批量添加字段 arcpy.AddField_management
arppy gis 读取text 并批量添加字段 arcpy.AddField_management 例:给“省级行政区域”添加“A、B、C、D” 4个字段。 (1)用Excel制作出字段及其描述表,定义字段结构; (2)复制除标题行以为的内…...

Pandas中at、iat函数详解
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 at 函数:通过行名和列名来取值(取行名为a, 列名为A的值) iat 函数:通过行号和列号来取值(取第1行,第1列的值) 本文给出at、iat常见的…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
