Codeforces Round 895 (Div. 3) A ~ F
Dashboard - Codeforces Round 895 (Div. 3) - Codeforces
A
问多少次能使a 和 b相等,就是abs(a - b) / 2除c向上取整,也就是abs(a - b)除2c向上取整。
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;void solve()
{int a, b, c;cin >> a >> b >> c;a = abs(a - b), c *= 2;cout << (a + c - 1) / c << endl;
}int main()
{IOSint _;cin >> _;while(_ --){solve();}return 0;
}B
真是一篇好阅读理解,读了好久
就是说陷阱会在踩到后经过s秒触发,触发后不能通过,最少往前走d + s / 2(向上取整)格子后就回不来了,把所有的d + s / 2比较取最小值然后减一就是答案。
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;void solve()
{int n;cin >> n;int ans = 2e9;for(int i = 0; i < n; i ++){int a, b;cin >> a >> b;a = a + (b + 1) / 2;ans = min(ans, a);}cout << ans - 1 << endl;
}int main()
{IOSint _;cin >> _;while(_ --){solve();}return 0;
}C
如果是>2的偶数的话,x - 2和x就是一组解
如果l == r且l是奇数的话,可以求l的因子,设因子为d,x - d 和 d 都可以被d整除,这样也可以求出一组解
之后注意一些边界条件就好了。
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;void solve()
{int l, r;cin >> l >> r;if(r < 4){cout << -1 << endl;return;}if(r % 2 && l == r){for(int i = 2; i * i <= l; i ++){if(l % i == 0){cout << l - i << ' ' << i << endl;return;}}cout << -1 << endl;return;}if(r % 2){cout << r - 3 << ' ' << 2 << endl;}else cout << r - 2 << ' ' << 2 << endl;
}int main()
{IOSint _;cin >> _;while(_ --){solve();}return 0;
}D
贪心。
设lcm为x和y的最大公倍数,lcm的倍数的位置有重合,先加后减等于零,在这里操作是没意义的。
加操作有意义的点的数量:n / x - n / lcm
减操作有意义的点的数量:n / y - n / lcm
加的话从n开始加,依次递减n-1、n-2这样
减的话从1开始加,依次递增2、3这样。
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;void solve()
{ll n, x, y;cin >> n >> x >> y;ll gcd = __gcd(x, y);ll lcm = x * y / gcd;ll a = n / x - n / lcm, b = n / y - n / lcm;a = a * (2 * n - a + 1) / 2;b = b * (b + 1) / 2;cout << a - b << endl;
}int main()
{IOSint _;cin >> _;while(_ --){solve();}return 0;
}E
前缀和。
做出这道题需要了解的两个性质:
1. x ^ x = 0;
2. 0 ^ x = x;
根据这两条性质我们就可以求出任意一段连续区间的异或和,使用前缀数组实现,用b[]表示
b[n]表示从第一项异或到第n项
b[r] ^ b[l - 1]就等于 b[l - 1] ^ b[l] ^ ... ^ b[r] ^ b[l - 1] = b[l] ^ ... ^ b[r];
对于第一个操作,区间修改,如果一个数x的对应位置上的树为1,被修改后变成0,就相当于x没被启用,变成0了,就相当于异或x本身,
如果一个数x的对应位置上的树为0,被修改后变成1,就相当于x被启用了,变成了1,也相当于异或x本身。
先用一个ans计算出被启用的数的异或和,之后每进行一次区间修改就相当于异或一遍这个区间内的异或和,非常的easy。
然后第二个操作,如果是查1,直接输出ans就好了
如果是查2,输出前n项异或前缀和异或ans就好了
听说有人线段树过了,挺nb的,之后再学一学。
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 100010;int a[N], b[N];void solve()
{int n;cin >> n;for(int i = 1; i <= n; i ++){cin >> a[i];b[i] = b[i - 1] ^ a[i]; }string s;cin >> s;s = ' ' + s;int ans = 0;for(int i = 1; i <= n; i ++){if(s[i] == '1'){ans ^= a[i];}}int Q;cin >> Q;while(Q --){int op;cin >> op;if(op == 1){int l, r;cin >> l >> r;int res = b[r] ^ b[l - 1];ans ^= res;}else{int x;cin >> x;if(x == 1)cout << ans << ' ';else cout << (b[n] ^ ans) << ' ';}}cout << endl;
}int main()
{IOSint _;cin >> _;while(_ --){solve();}return 0;
}赛后学的线段树做法:
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 100010;int n;
int a[N];
string s;
struct Node
{int l, r;int sum0, sum1;int f;
}tr[N * 4];void pushup(int u)
{tr[u].sum0 = tr[u << 1].sum0 ^ tr[u << 1 | 1].sum0;tr[u].sum1 = tr[u << 1].sum1 ^ tr[u << 1 | 1].sum1;
}void pushdown(int u)
{Node &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];if(tr[u].f){swap(left.sum0, left.sum1);swap(right.sum0, right.sum1);left.f ^= tr[u].f;right.f ^= tr[u].f;tr[u].f = 0;}
}void build(int u, int l, int r)
{if(l == r){if(s[l] == '0')tr[u] = {l, r, a[l], 0, 0};else tr[u] = {l, r, 0, a[l], 0};}else{tr[u] = {l, r, 0, 0, 0};int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);pushup(u);}
}void modify(int u, int l, int r)
{if(tr[u].l >= l && tr[u].r <= r){swap(tr[u].sum0, tr[u].sum1);tr[u].f ^= 1;}else{pushdown(u);int mid = tr[u].l + tr[u].r >> 1;if(l <= mid)modify(u << 1, l, r);if(r > mid)modify(u << 1 | 1, l, r);pushup(u);}
}void solve()
{cin >> n;for(int i = 1; i <= n; i ++)cin >> a[i];cin >> s;s = ' ' + s;build(1, 1, n);int Q;cin >> Q;while(Q --){int op;cin >> op;if(op == 1){int l, r;cin >> l >> r;modify(1, l, r);}else{int x;cin >> x;if(x == 0)cout << tr[1].sum0 << ' ';else cout << tr[1].sum1 << ' ';}}cout << endl;
}int main()
{IOSint _;cin >> _;while(_ --){solve();}return 0;
}Node节点存两个值sum0和sum1,f作为懒标记。
F
i在要a[i]之前被卖出,其实就是拓扑排序,先输出没在环中的点,然后每个环中,值最小的那个点最后卖出一定是最优的,类似贪心。
其实我在想如果一个点同时出现在两个环中该怎么办,然后发现这种情况其实不存在
比如
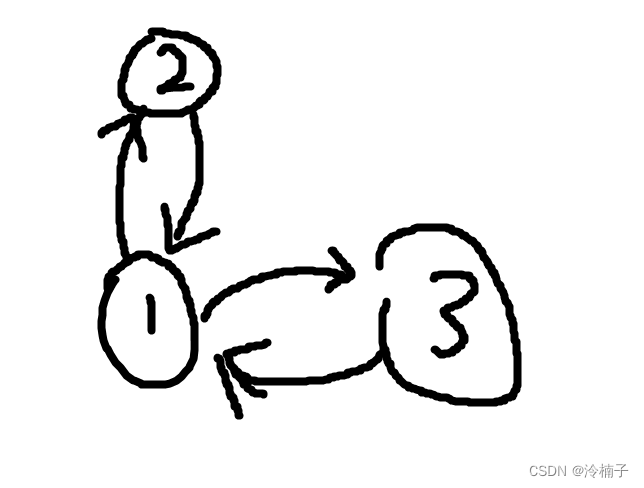
如果一个点出现在多个环中,边数会比点数还多,因为又要求每个点的出度都为1,所以这种情况显然是与输入要求矛盾的,所以一个点一定最多出现在一个环内,证毕。
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 100010;int n;
int h[N], e[N], ne[N], idx;
int d[N];
int a[N], b[N];
bool st[N];
vector<int> ans;
queue<int> q;void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}void bfs()
{while(q.size()){int t = q.front();q.pop();ans.push_back(t);for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];if(st[j])continue;d[j] --;if(!d[j]){q.push(j);st[j] = true;}}}
}void solve()
{idx = 0;ans.clear();cin >> n;priority_queue<PII, vector<PII>, greater<PII>> heap;for(int i = 1; i <= n; i ++)d[i] = 0;for(int i = 1; i <= n; i ++){st[i] = false;h[i] = -1;cin >> a[i];add(i, a[i]);d[a[i]] ++;}for(int i = 1; i <= n; i ++){cin >> b[i];heap.push({b[i], i});if(!d[i]){st[i] = true;q.push(i);}}bfs();while(ans.size() < n){int ver;while(heap.size()){PII t = heap.top();heap.pop();if(!st[t.second]){ver = t.second;break;}}st[ver] = true;for(int i = h[ver]; i != -1; i = ne[i]){int j = e[i];if(st[j])continue;d[j] --;if(!d[j]){q.push(j);st[j] = true;}}bfs();ans.push_back(ver);}for(int i = 0; i < n; i ++)cout << ans[i] << ' ';cout << endl;}int main()
{IOSint _;cin >> _;while(_ --){solve();}return 0;
}相关文章:

Codeforces Round 895 (Div. 3) A ~ F
Dashboard - Codeforces Round 895 (Div. 3) - Codeforces A 问多少次能使a 和 b相等,就是abs(a - b) / 2除c向上取整,也就是abs(a - b)除2c向上取整。 #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); #de…...

【前端知识】Axios——请求拦截器模板
Axios——请求拦截器模板 Axios是一个基于Promise的HTTP客户端,用于发送HTTP请求。它可以在浏览器和Node.js环境中使用,并且提供了许多强大的功能,例如拦截请求和响应、转换请求和响应数据、取消请求等。 Axios具有简单易用的API,…...
企业架构LNMP学习笔记16
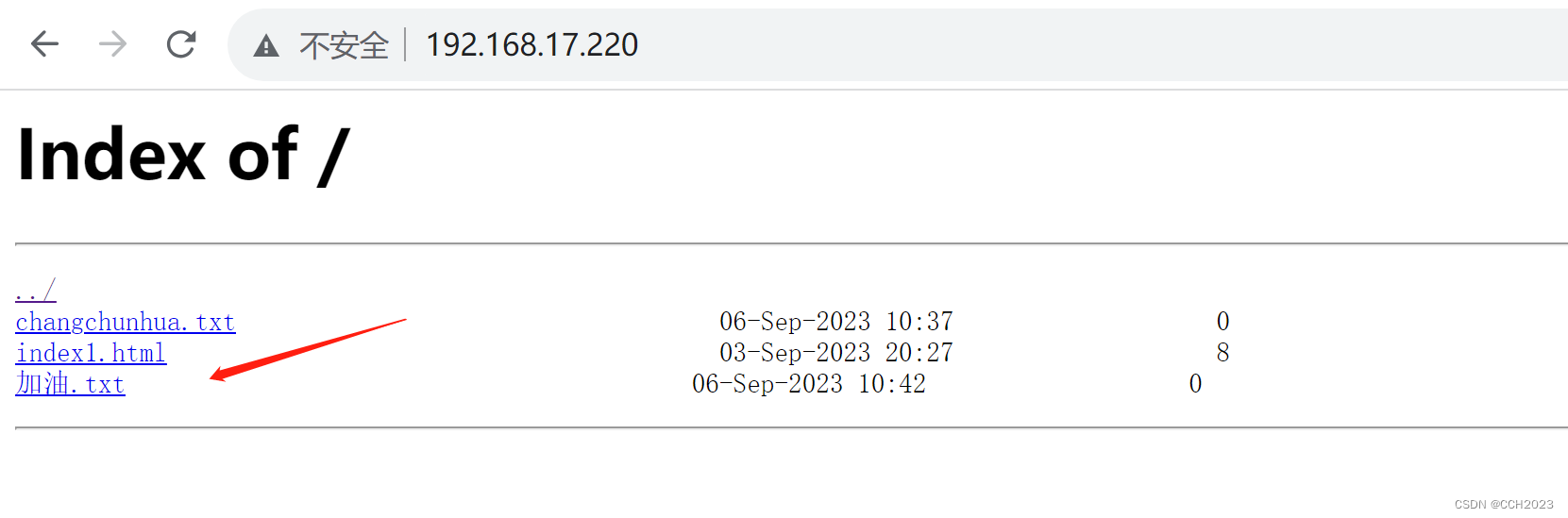
基于IP的访问控制: 基于ngx_http_access_module模块,默认可使用。 语法是: deny ip 禁止IP访问 allow ip 允许IP访问 上面是允许的,下面是deny的。 老师建议写在server段中是比较合适的。 基于用户的访问控制: …...
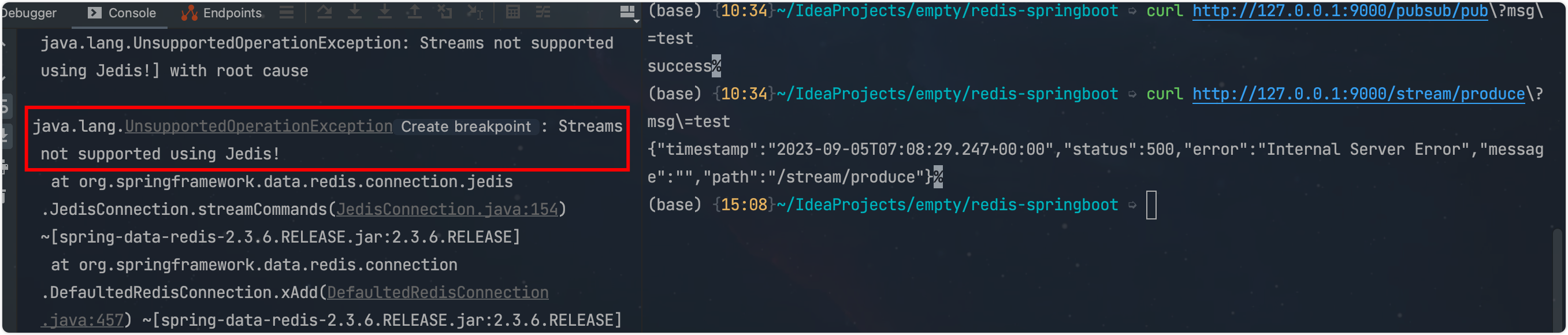
redis实现消息队列
背景 消息队列(Message Queue)是一种常见的软件架构模式,用于在分布式系统中传递和处理异步消息。它解耦了发送消息的应用程序和接收消息的应用程序之间的直接依赖关系,使得消息的发送者和接收者可以独立地演化和扩展。 消息队列…...

JVM指令集
概述 JVM,Java Virtual Machine,Java虚拟机器,作为一台独立的机器,一般包括独立的指令集、独立的存储体系以及适合机器自身的运算方式,本章节主要是描述JVM指令的功能与作用。 JVM的每个指令的格式是【指令 操作数1操…...
如何用SSH克隆GitHub项目
诸神缄默不语-个人CSDN博文目录 使用场景:由于不可知的网络问题,无法用HTTPS克隆GitHub项目。 报错fatal: unable to access https://github.com/PolarisRisingWar/llm-throught-ages.git/: GnuTLS recv error (-110): The TLS connection was non-pro…...

sqlx库使用指南
sqlx库使用指南 在项目中我们通常可能会使用database/sql连接MySQL数据库。本文借助使用sqlx实现批量插入数据的例子,介绍了sqlx中可能被你忽视了的sqlx.In和DB.NamedExec方法。 sqlx介绍 在项目中我们通常可能会使用database/sql连接MySQL数据库。sqlx可以认为是Go…...

算法篇汇总
文章浏览 I https://leetcode.cn/problems/article-views-i/description/?envTypestudy-plan-v2&envId30-days-of-pandas&langpythondata 我的题解: import pandas as pddef article_views(views: pd.DataFrame) -> pd.DataFrame:dfviews[views[auth…...
typeScript 学习笔记(二)
类接口 TypeScript 入门教程 (xcatliu.com) 十四.类 ① 类 类:定义了一件事物的抽象特点,包含它的属性和方法对象:类的实例,通过new生成面向对象(OOP)的三大特性:封装、继承、多态封装&…...

redis集群架构详解
一、集群架构搭建 1、配置 在一台机器上模拟多台机器搭建redis集群,一个集群代表一台物理机 集群1路径: /usr/local/redis/redis-cluster/cluster1/9001/redis.conf/usr/local/redis/redis-cluster/cluster1/9004/redis.conf/usr/local/redis/redis-…...

nodejs设置镜像
1、npm镜像地址配置 -- 查看 npm 安装目录 npm root -g-- 查看 npm 配置信息 npm config list-- 查询当前镜像配置 npm get registry-- 或者仅修改 npm 命令镜像 -- 设置为淘宝镜像 npm config set registry https://registry.npmmirror.com -- 修改为官方镜像 npm config set…...

CSS中如何在table中隐藏表格中从第4个开始的多个 <tr> 元素
隐藏指定行 使用 CSS 的 nth-child 选择器来选择表格中的特定行,并隐藏它们。 以下是一个示例 CSS 规则,用于隐藏表格中的第 4 个和第 5 个行(索引从 1 开始): table tr:nth-child(4), table tr:nth-child(5) {displ…...

【类和对象】③友元类
文章目录 1.初始化列表2.static静态成员3.友元 1.初始化列表 我们知道在创建对象时,编译器通过调用构造函数,给对象中各个成员变量一个合适的初始值。虽然调用构造函数之后,对象中已经有了一个初始值,但是不能将其称为对对象中成…...

算法通关村第十六关:黄金挑战:滑动窗口与堆结合
黄金挑战:滑动窗口与堆结合 堆的大小一般是有限的,能直接返回当前位置下的最大值或者最小值 该特征与滑动窗口结合,可以解决一些特定场景的问题 1. 滑动窗口与堆问题的结合 LeetCode239 https://leetcode.cn/problems/sliding-window-maxi…...

6.2.2 【MySQL】InnoDB中的索引方案
上边之所以称为一个简易的索引方案,是因为我们为了在根据主键值进行查找时使用二分法快速定位具体的目录项而假设所有目录项都可以在物理存储器上连续存储,但是这样做有几个问题: InnoDB 是使用页来作为管理存储空间的基本单位,也…...

划片机实现装片、对准、切割、清洗到卸片的自动化操作
划片机是一种用于切割和分离材料的设备,通常用于光学和医疗、IC、QFN、DFN、半导体集成电路、GPP/LED氮化镓等芯片分立器件、LED封装、光通讯器件、声表器件、MEMS等行业。划片机可以实现从装片、对准、切割、清洗到卸片的自动化操作。 以下是划片机实现这些操作的步…...

OpenCV(二十五):边缘检测(一)
目录 1.边缘检测原理 2.Sobel算子边缘检测 3.Scharr算子边缘检测 4.两种算子的生成getDerivKernels() 1.边缘检测原理 其原理是基于图像中灰度值的变化来捕捉图像中的边界和轮廓。梯度则表示了图像中像素强度变化的强弱和方向。 所以沿梯度方向找到有最大梯度值的像素&…...

上行取消指示 DCI format 2_4
上篇介绍了DCI format 2_1的DL传输中断的内容,这篇就看下DCI format 2_4有关的UL 传输取消机制,值得注意的是这里的UL传输针对的是PUSCH和SRS传输。 UL cancellation DCI format 2_4相关机制引入的背景与DCI format 2_1一样,都是因为URLLC和e…...
百望云蝉联2023「Cloud 100 China 」榜单 综合实力再获认可
9月7日,2023 Cloud 100 China 榜单于上海中心正式发布,榜单由靖亚资本与崔牛会联合推出,百望云凭借着过硬的综合实力与卓越的技术创新能力,再次荣登榜单,位居第六位。 本届评选,Top 100 企业的数据指标的权…...

力扣刷题班第1节:Python语法常遗漏的知识
以下仅仅记录和后面力扣刷题相关的、且平常会遗漏的语法知识。 下面这些笔记都是点到为止,不进行深入解释。大多数学过python的朋友看到就知道什么意思的,我就不解释了 字符串 str "I am a cook"# 按照空格切分 str.split(" ") …...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...
