自适应迭代扩展卡尔曼滤波算法AIEKF估计SOC VS 扩展卡尔曼估计SOC
自适应迭代扩展卡尔曼滤波算法(AIEK)
自适应迭代扩展卡尔曼滤波算法(AIEK)是一种滤波算法,其目的是通过迭代过程来逐渐适应不同的状态和环境,从而优化滤波效果。
该算法的基本思路是在每一步迭代过程中,根据所观测的数据和状态方程,对滤波器的参数进行自适应调整,以便更好地拟合实际数据的分布。具体而言,该算法包括以下步骤:
初始化:首先,为滤波器的初始参数设定一个初始值,这些参数包括状态转移矩阵、测量矩阵、过程噪声协方差和测量噪声协方差等。
预测:根据当前的状态方程和滤波器参数,对下一个状态进行预测,并计算预测误差。
校正:根据预测结果和实际观测数据,对预测进行修正,以便更好地拟合实际数据的分布。
参数更新:根据校正结果,自适应地调整滤波器参数,以便在下一个迭代过程中更好地拟合数据。
该算法具有自适应性和迭代性,能够逐渐适应不同的状态和环境,从而优化滤波效果。在实际应用中,可以根据具体问题选择不同的滤波器参数调整方法和迭代策略,以获得更好的滤波效果。
加载待辨识工况数据
load FUDS.mat; %导入数据
Ut = FUDS.Voltage; %测量电压
I = FUDS.Current; %测量电流
cs0=[ 1.2761;-0.2899;0.0365;-0.0449;0.0095];
计算SOC实验数据
soc_act = nan(1,N);
ocv = nan(1,N);
soc_act(1)=1;
ocv(1)=Ut(1);
for i=2:Nsoc_act(i)=soc_act(i-1)-I(i)/(Qn);nihe=[1.936,-7.108,9.204,-4.603,1.33,3.416];ocv(i)=polyval(nihe,soc_act(i));
end
FFRLS参数在线辨识算法
[R0,R1,R2,C1,C2] = FFRLS(Ut,I,Qn,nihe,ff,cs0);% 辨识参数图
t=1:N;figure;
set(gcf,'Units','centimeters','Position',[2 2 19.6 8]);
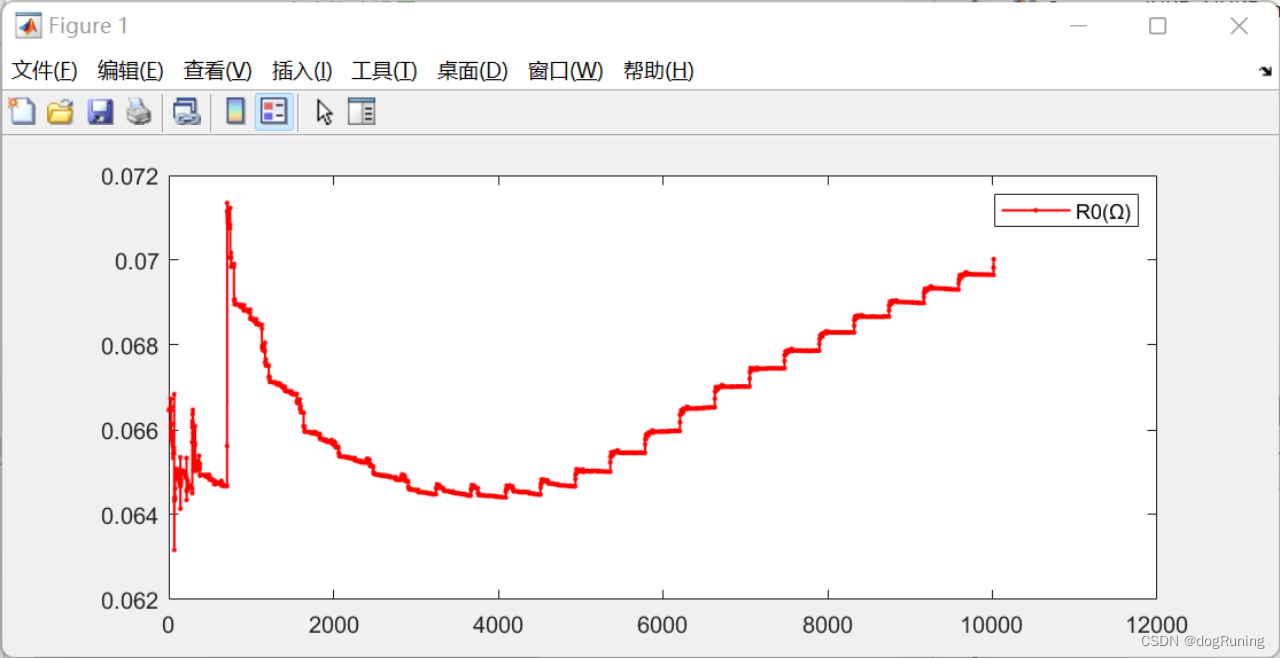
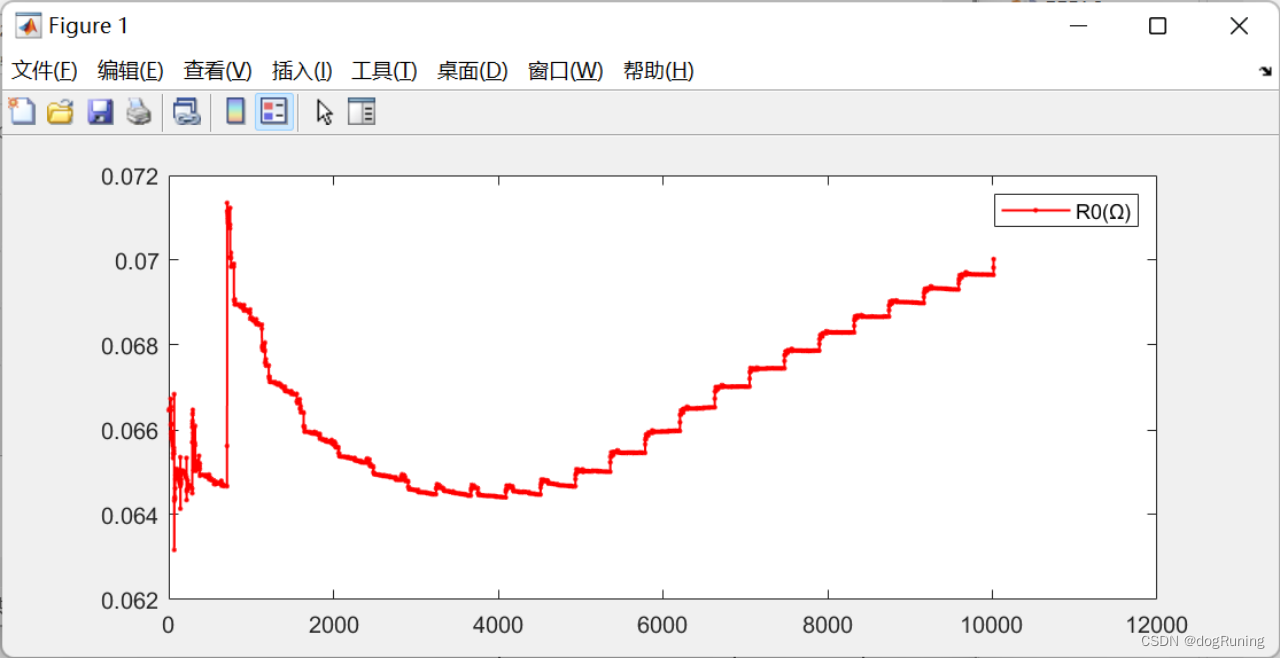
plot(t,R0,'r.-','LineWidth',1);
legend('R0(Ω)');figure;
set(gcf,'Units','centimeters','Position',[2 2 19.6 8]);
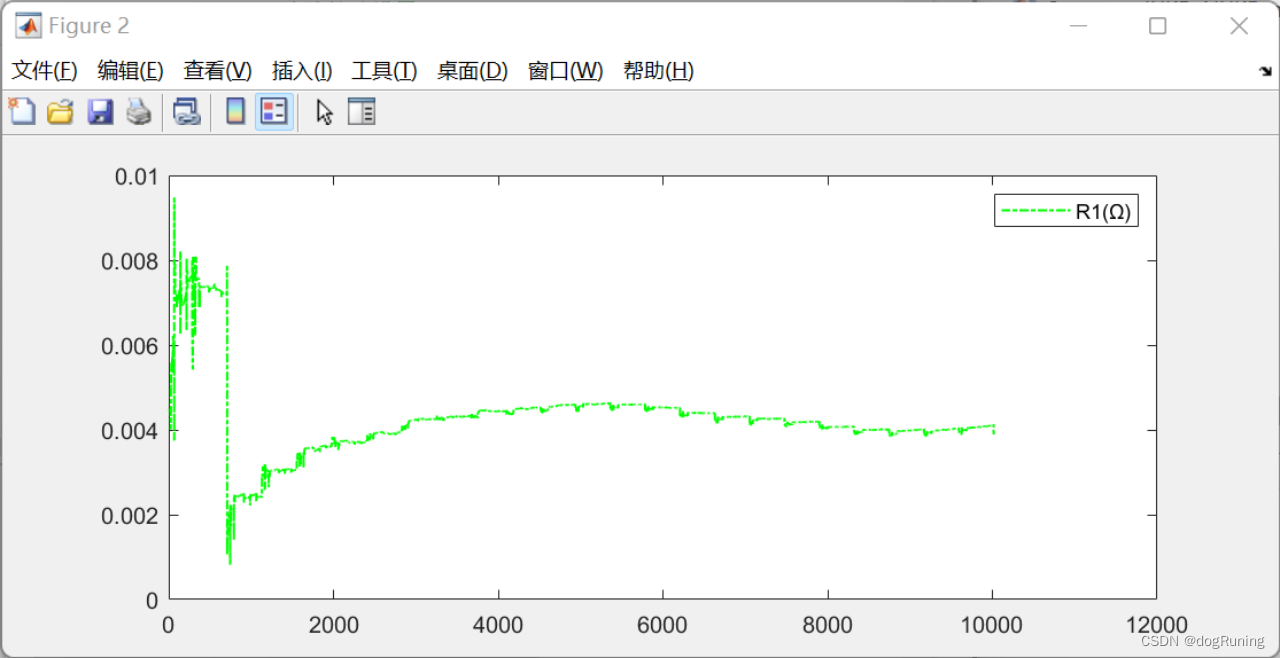
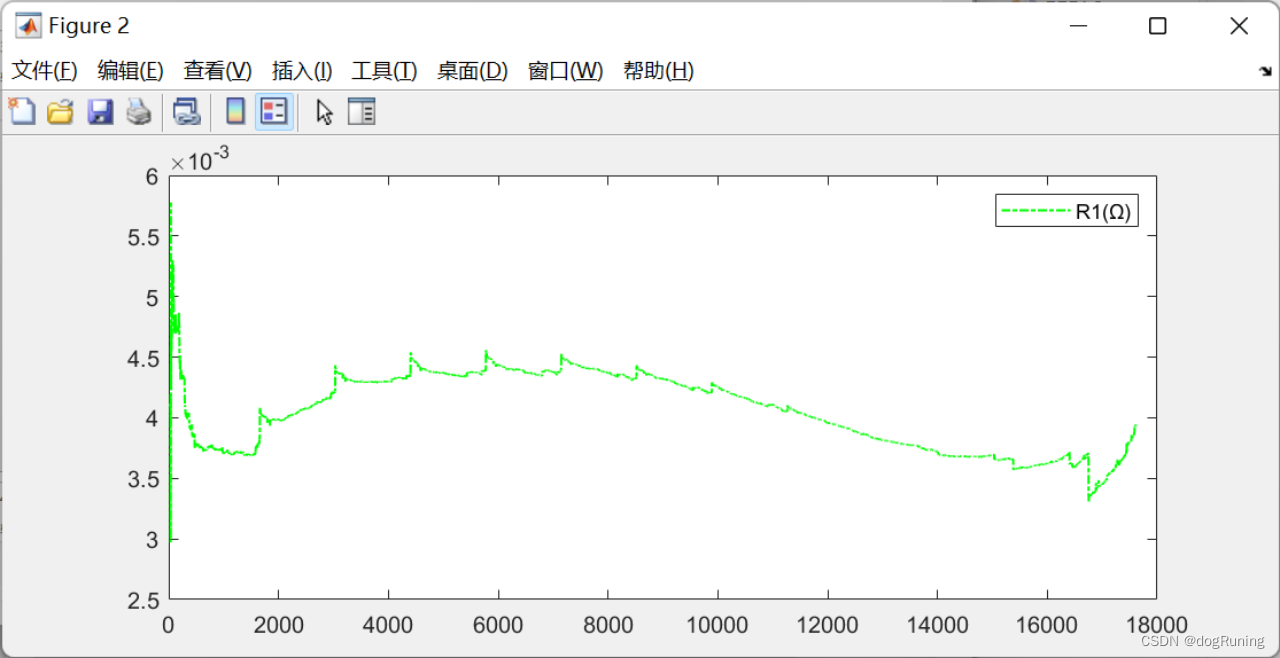
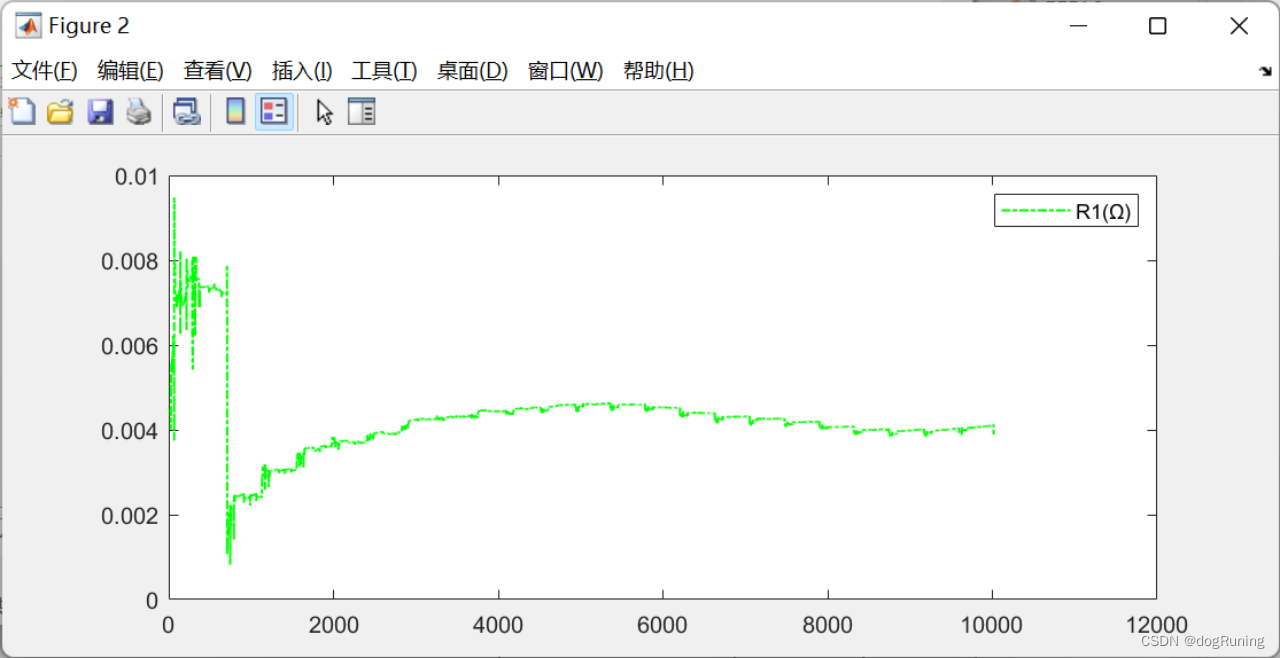
plot(t,R1,'g-.','LineWidth',1);
legend('R1(Ω)');figure;
set(gcf,'Units','centimeters','Position',[2 2 19.6 8]);
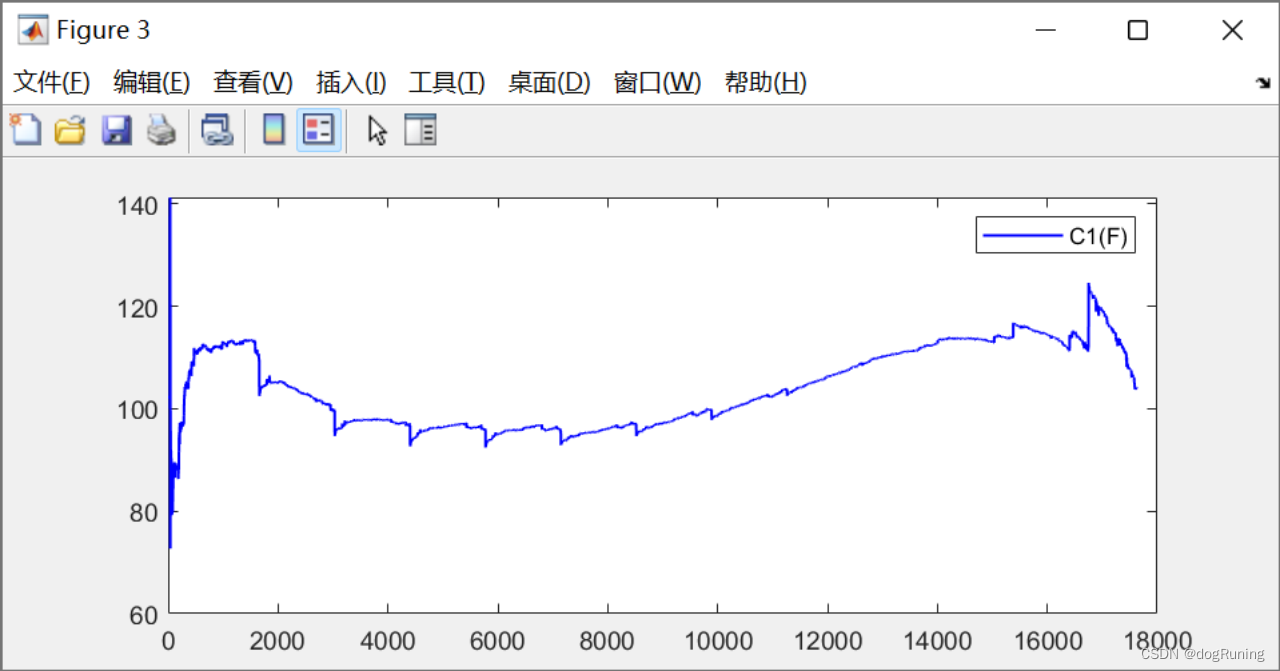
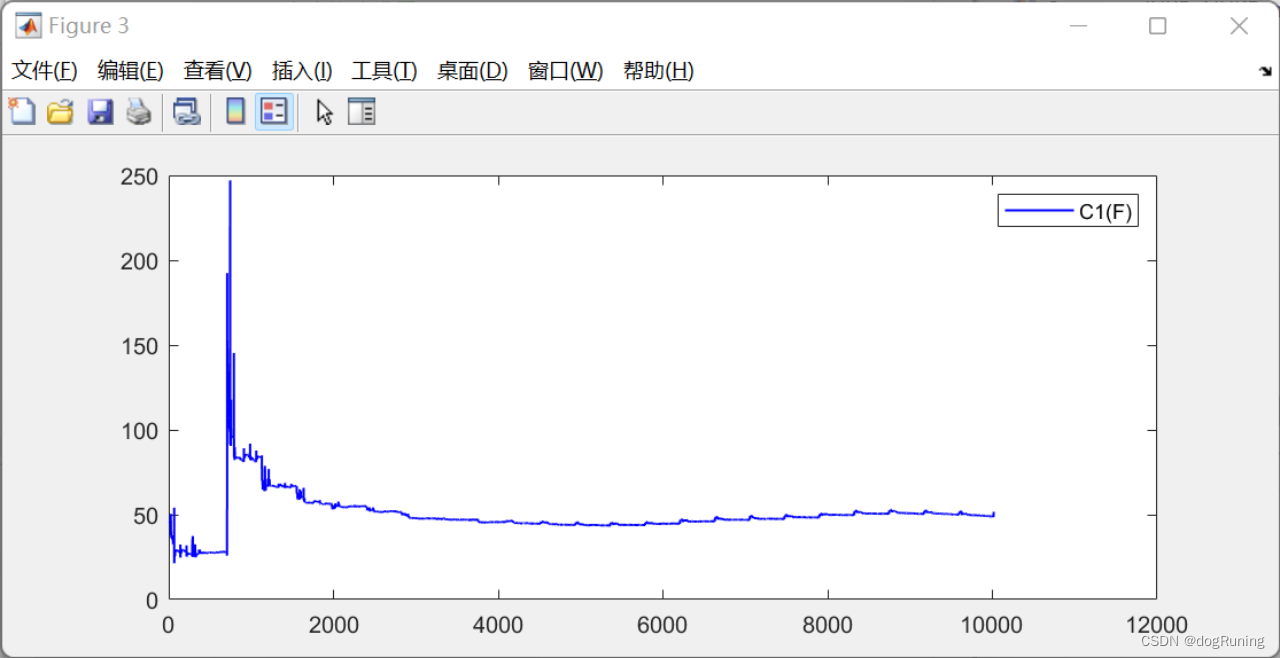
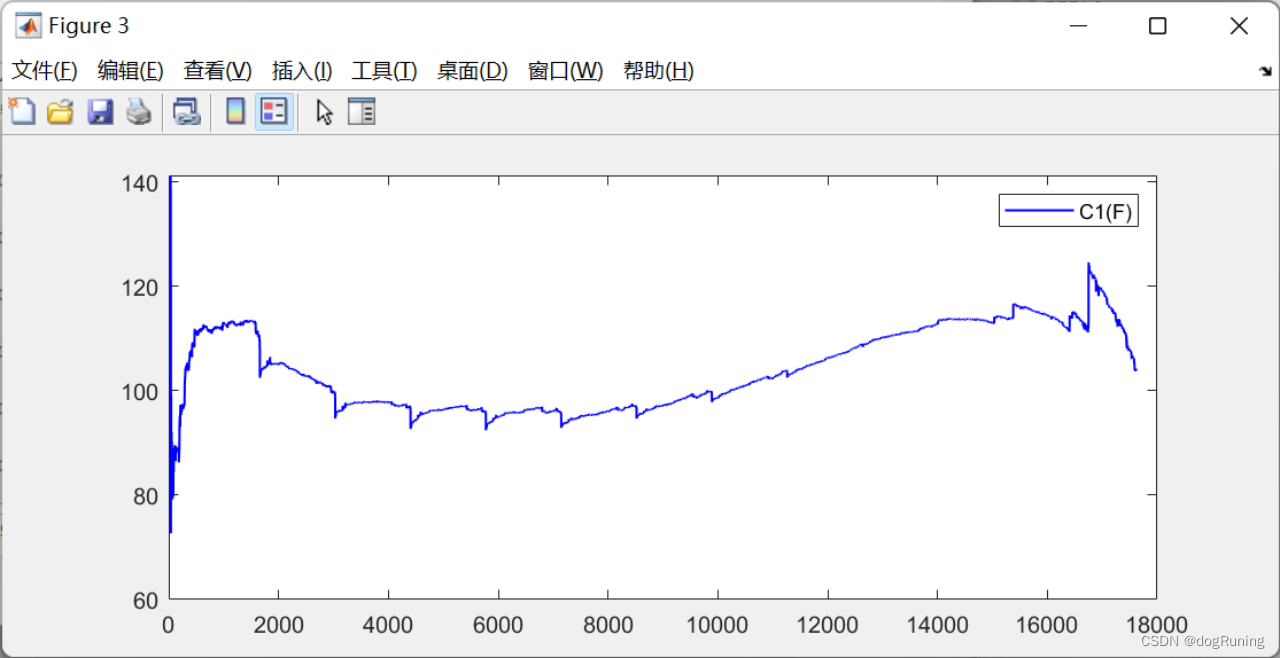
plot(t,C1,'b-','LineWidth',1);
legend('C1(F)');figure;
set(gcf,'Units','centimeters','Position',[2 2 19.6 8]);
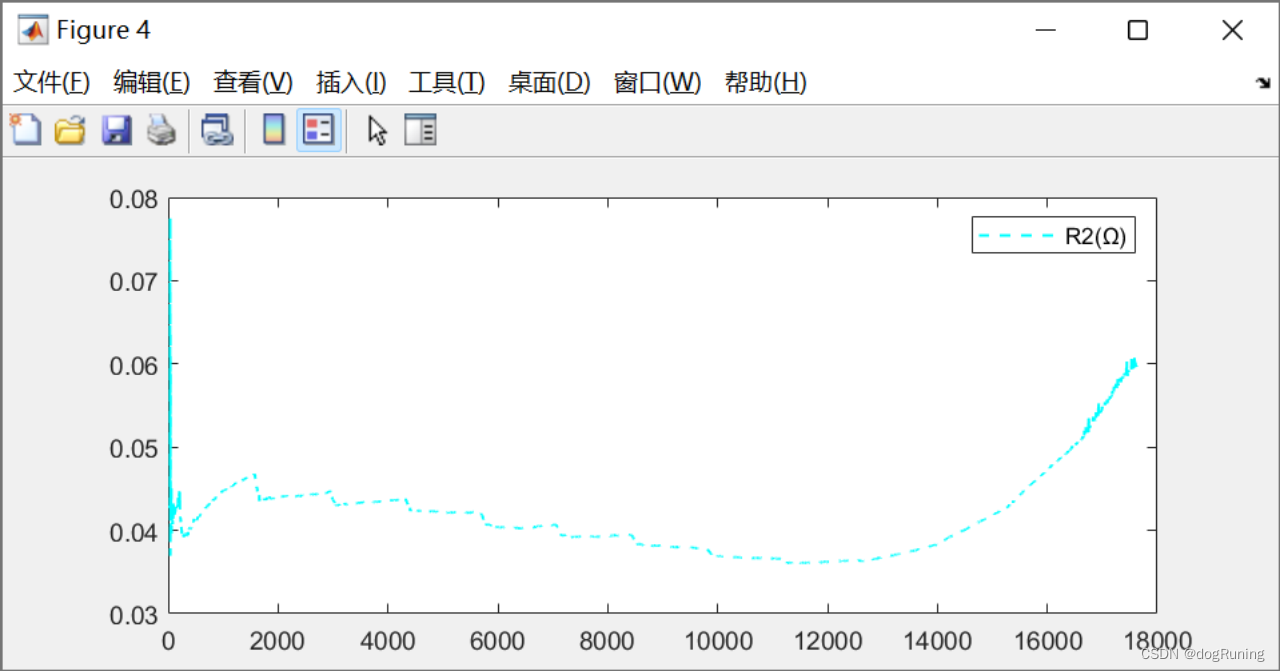
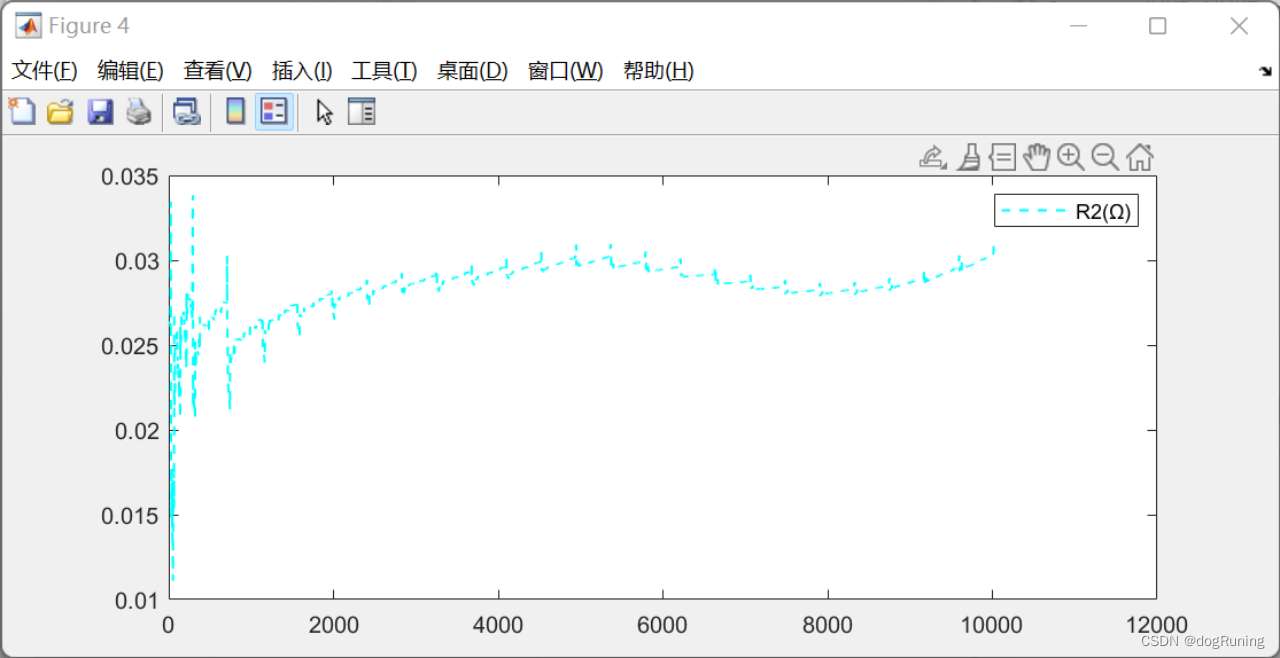
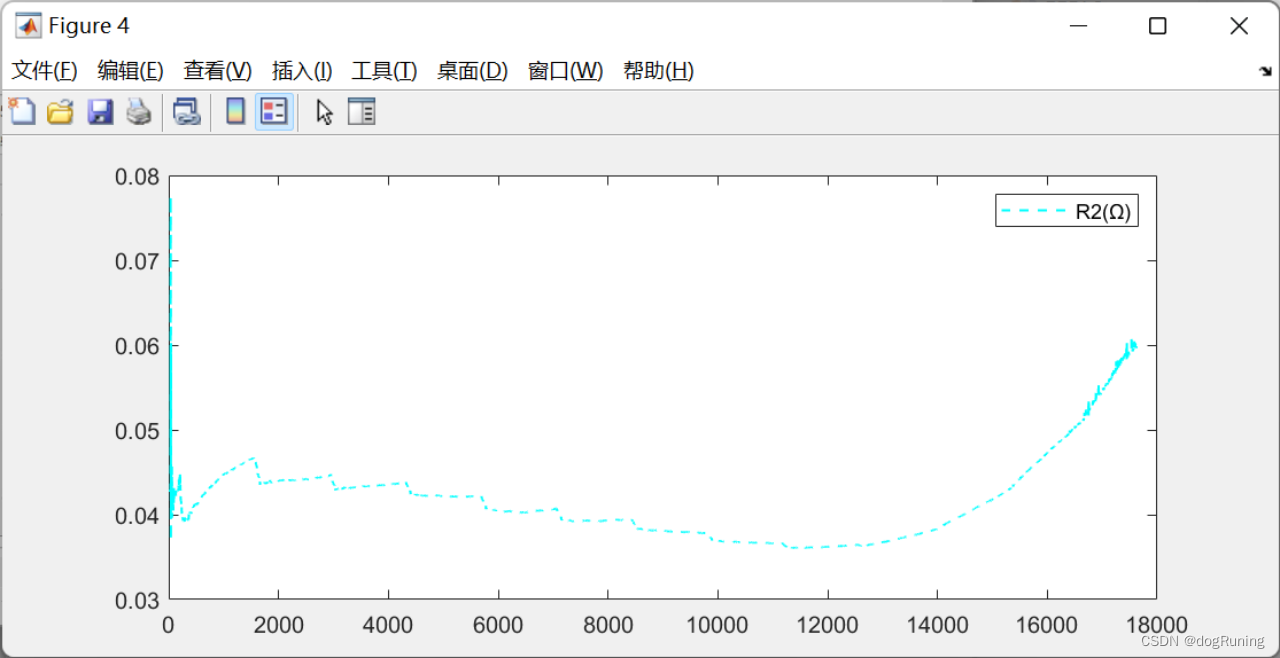
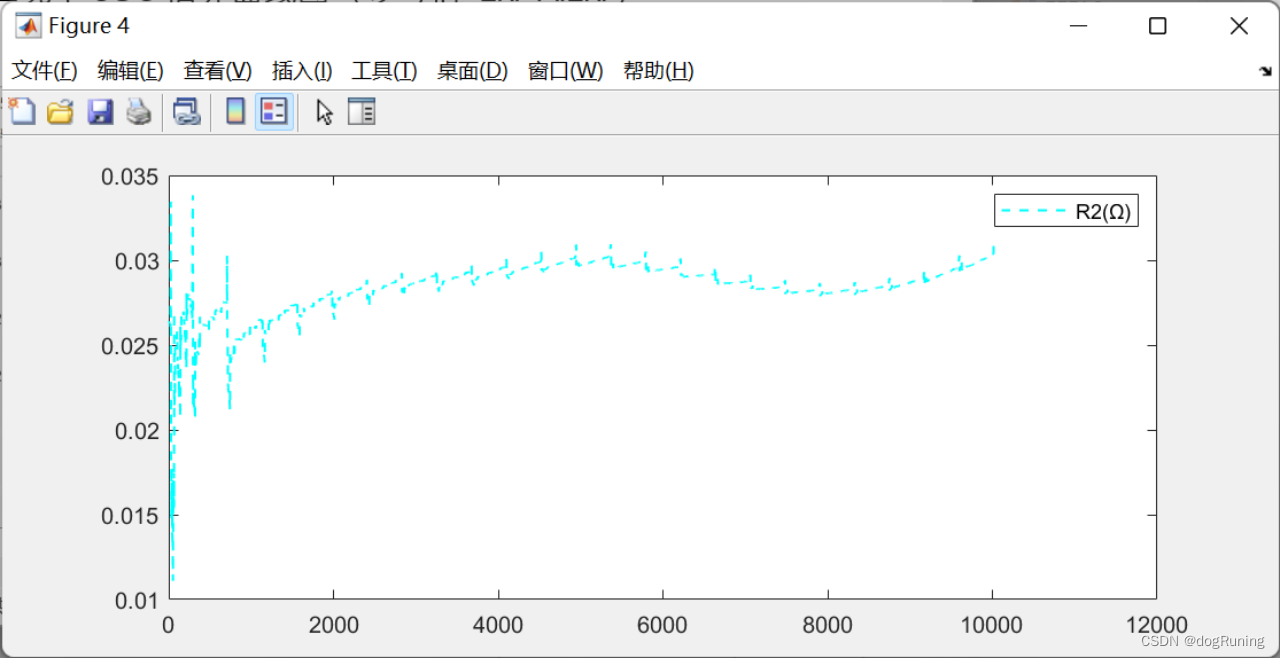
plot(t,R2,'c--','LineWidth',1);
legend('R2(Ω)');figure;
set(gcf,'Units','centimeters','Position',[2 2 19.6 8]);
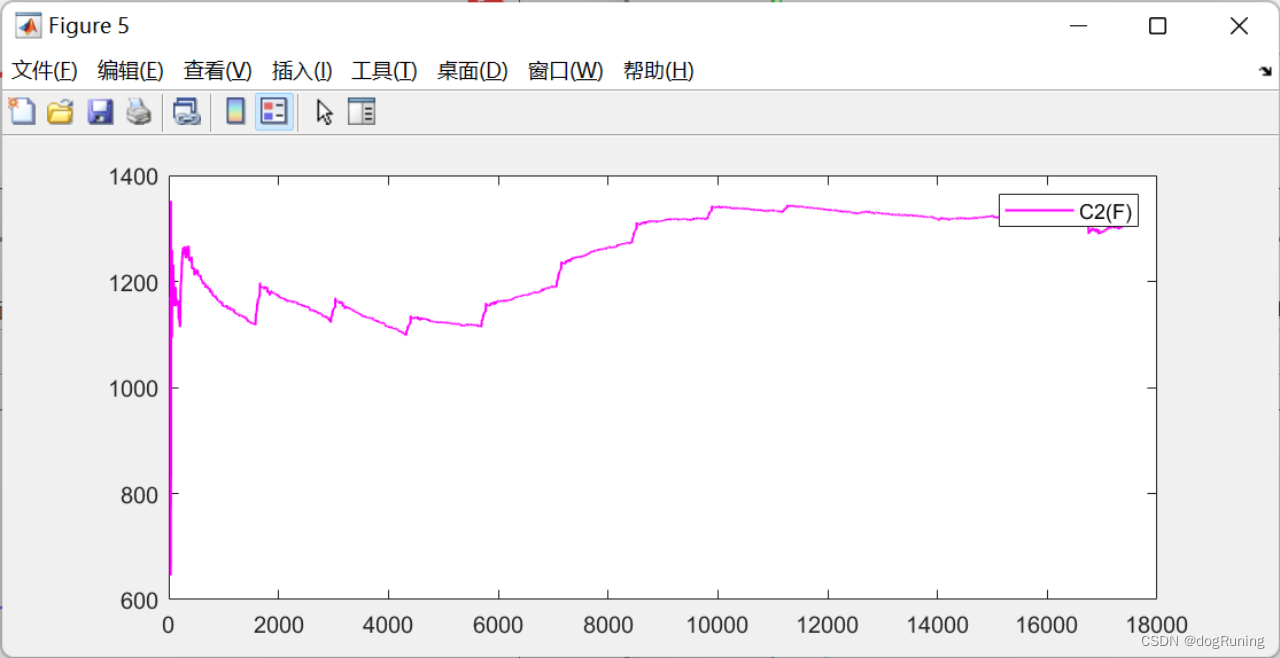
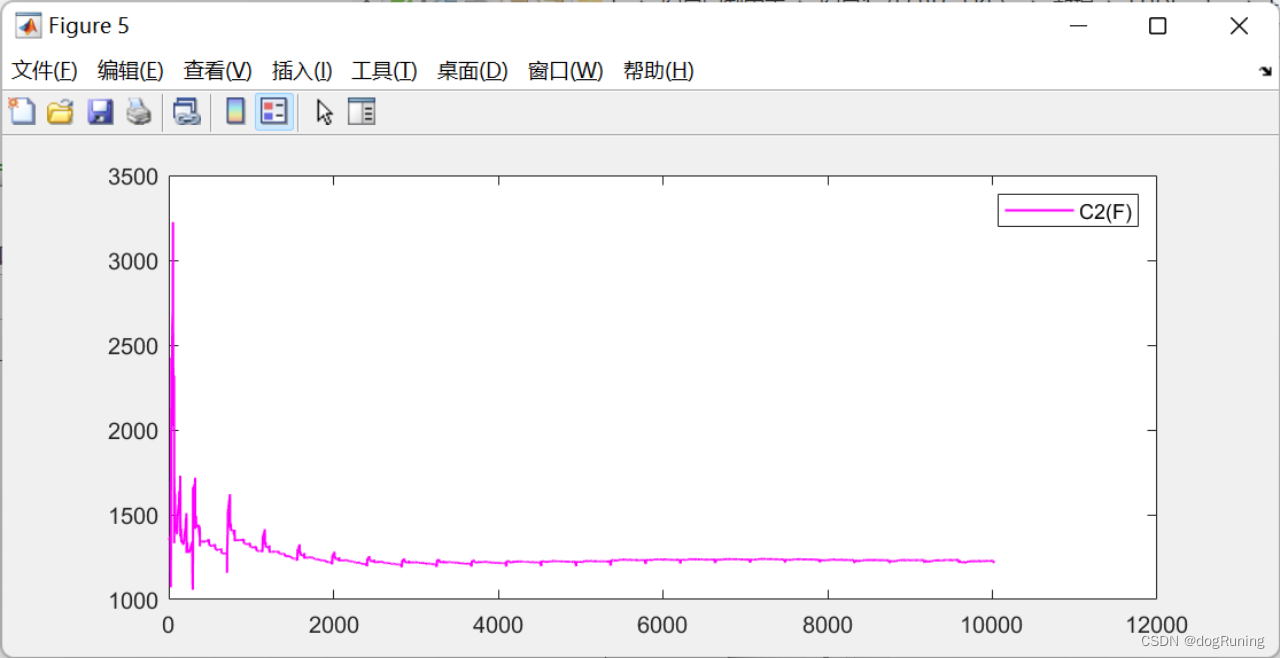
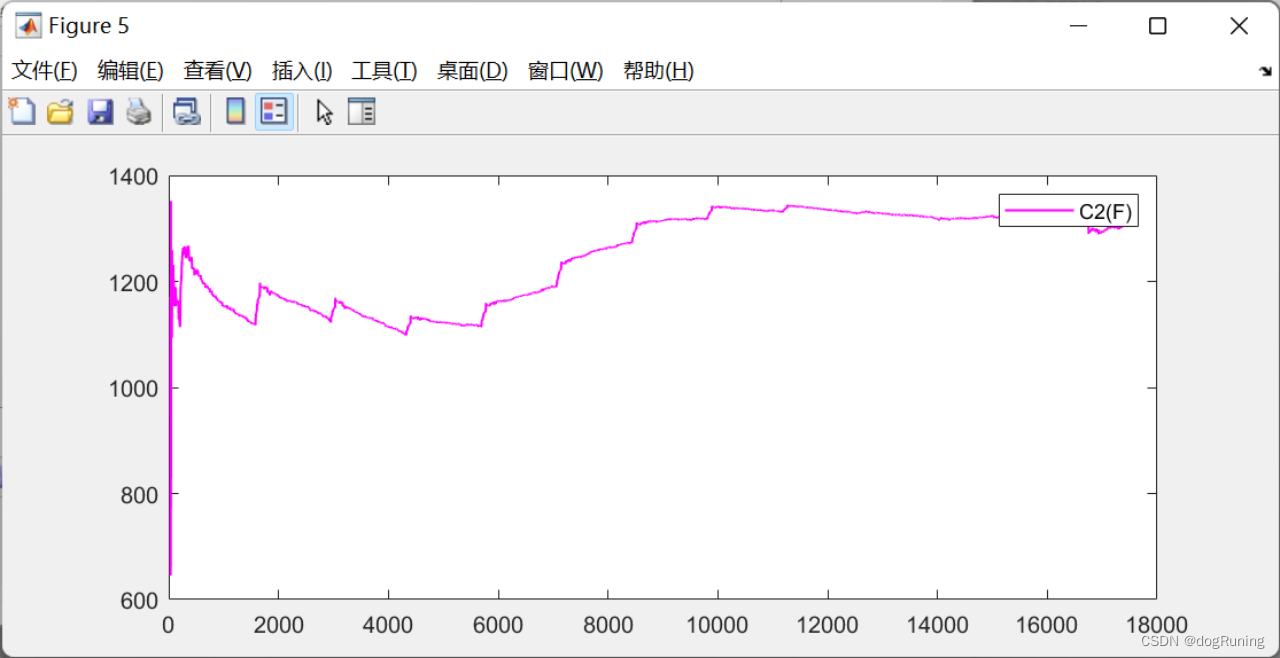
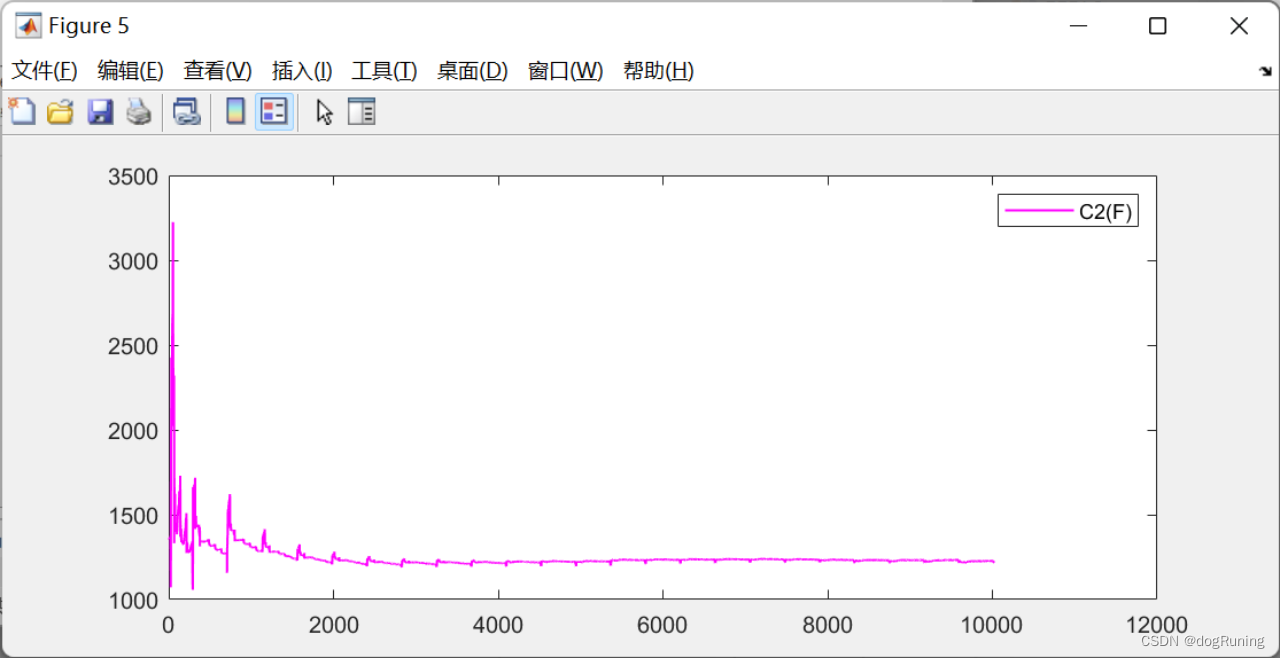
plot(t,C2,'m-','LineWidth',1);
legend('C2(F)');EKF滤波算法
SOCest_init=0.9;
P0=1e-3; %状态误差协方差初值
Q=1e-8; %过程噪声期望值
R=1; %观测噪声期望值[SOC_ekf,volt]=EKF(I,Ut,dt,Qn,SOCest_init,N,Q,R,nihe,P0,R0,R1,R2,C1,C2);
error_V_EKF= Ut'-volt;
error_SOC_EKF= soc_act-SOC_ekf; %滤波处理后的误差AIEKF滤波算法
X_aiekf=zeros(3,N); %定义状态向量x
X_aiekf(:,1)=[0;0;SOCest_init];%状态向量x初值设定
Q=1e-8;
R=1;
P0=0.01*eye(3);%定义协方差
f=0.1;
M=30; %误差积累值窗口系数
[SOC_aiekf,Um]=AIEKF(I',Ut',X_aiekf,f,M,Q,R,N,P0,R0,R1,R2,C1,C2,Qn,nihe);error_V_AIEKF= Ut'-Um;
error_SOC_AIEKF= soc_act-SOC_aiekf; %滤波处理后的误差
绘图
t=1:N;
figure;
set(gcf,'Units','centimeters','Position',[2 2 19.6 8]);
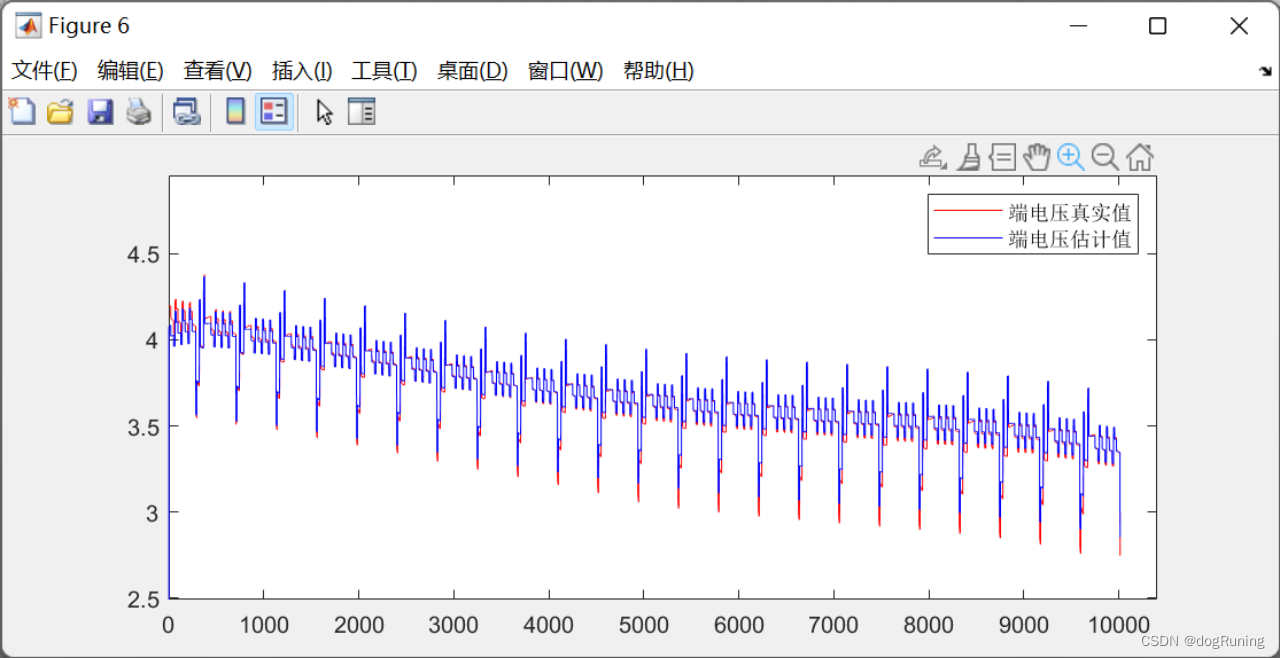
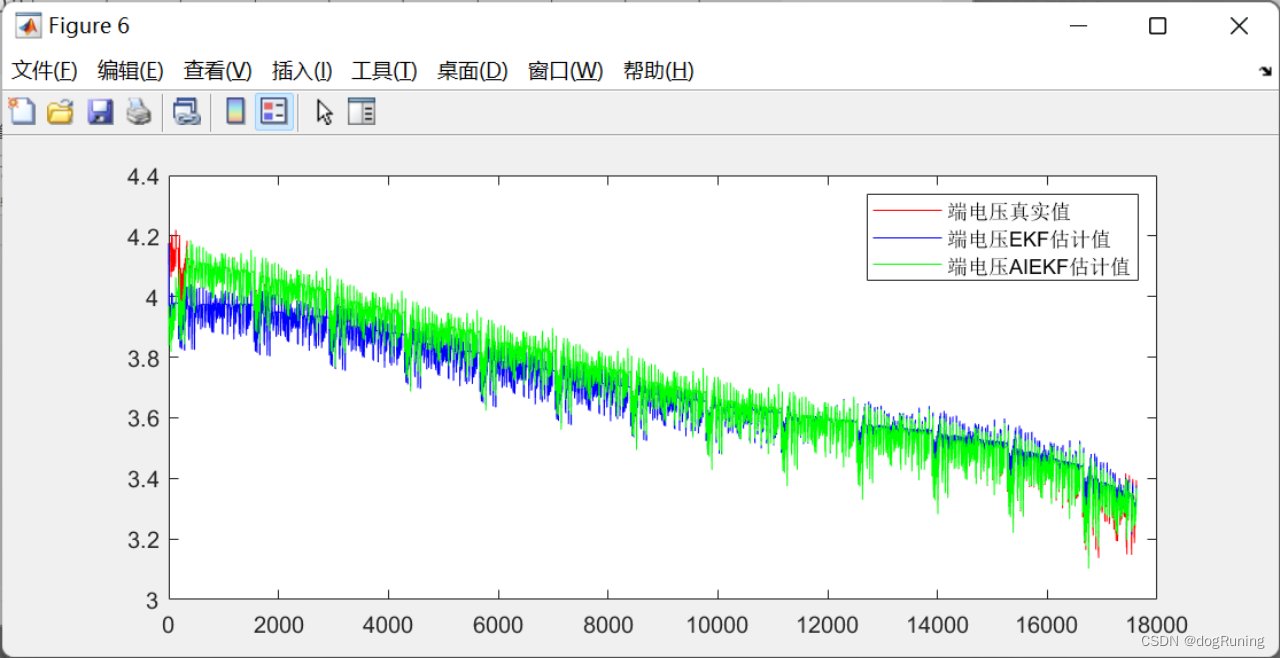
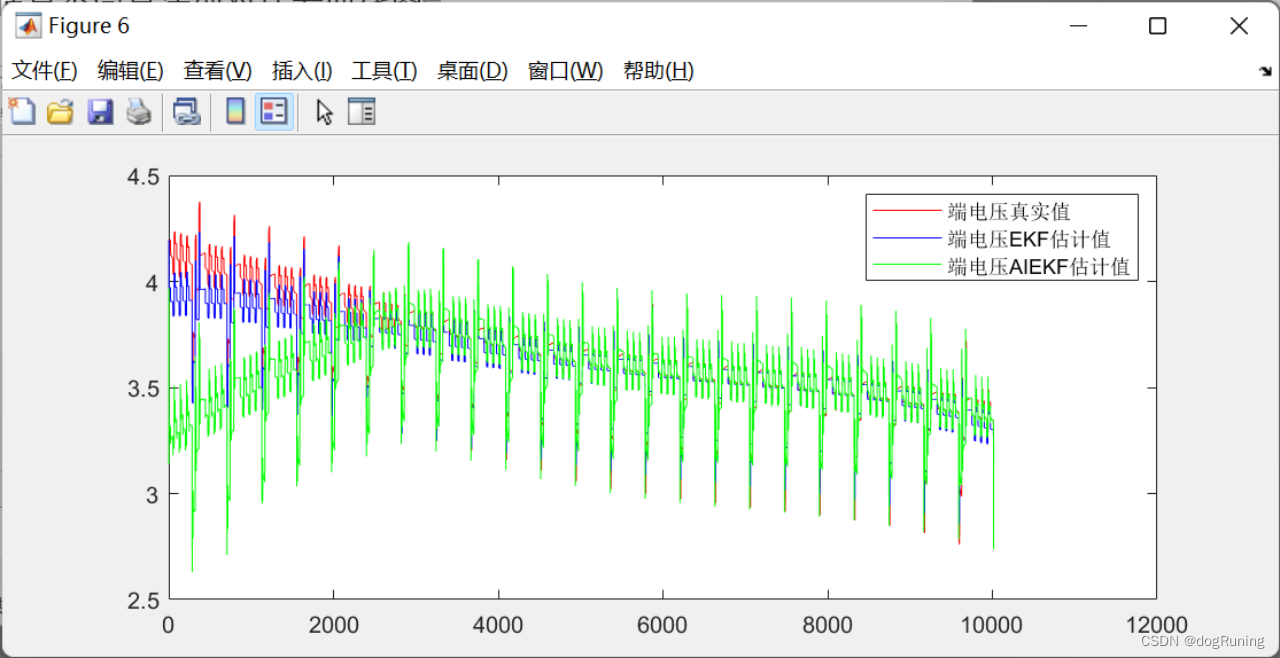
plot(t,Ut,'r',t,volt,'b',t,Um,'g');
legend('端电压真实值','端电压EKF估计值','端电压AIEKF估计值'); figure;
set(gcf,'Units','centimeters','Position',[2 2 19.6 8]);
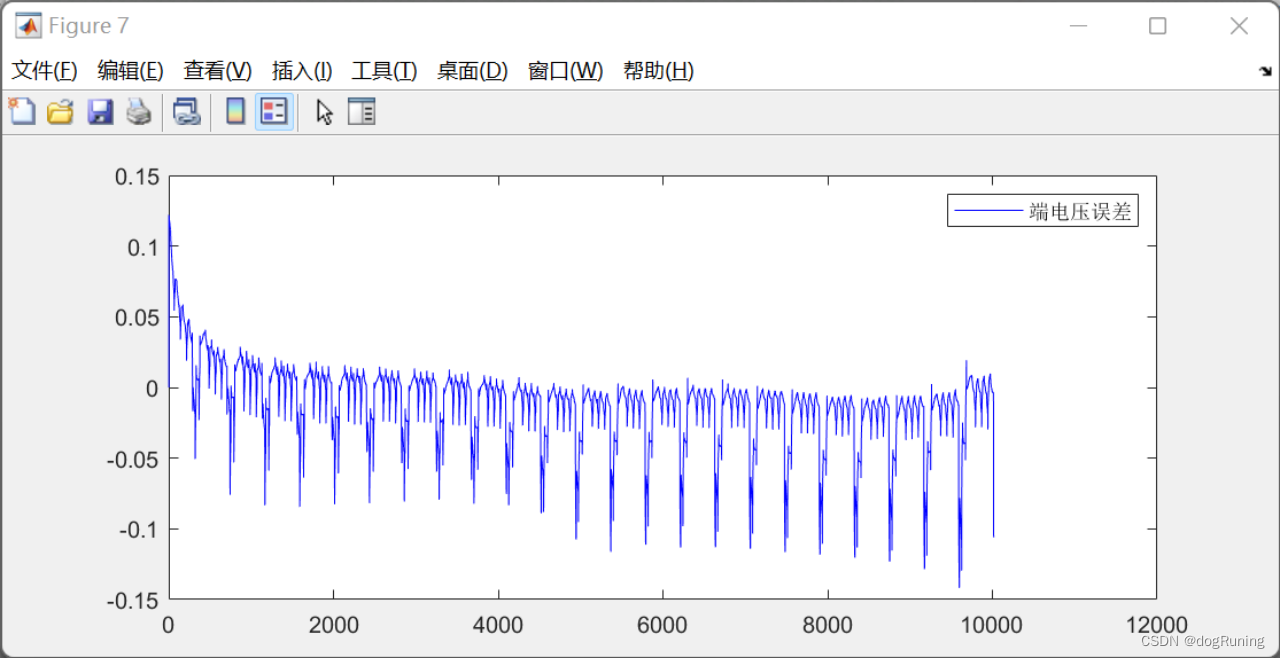
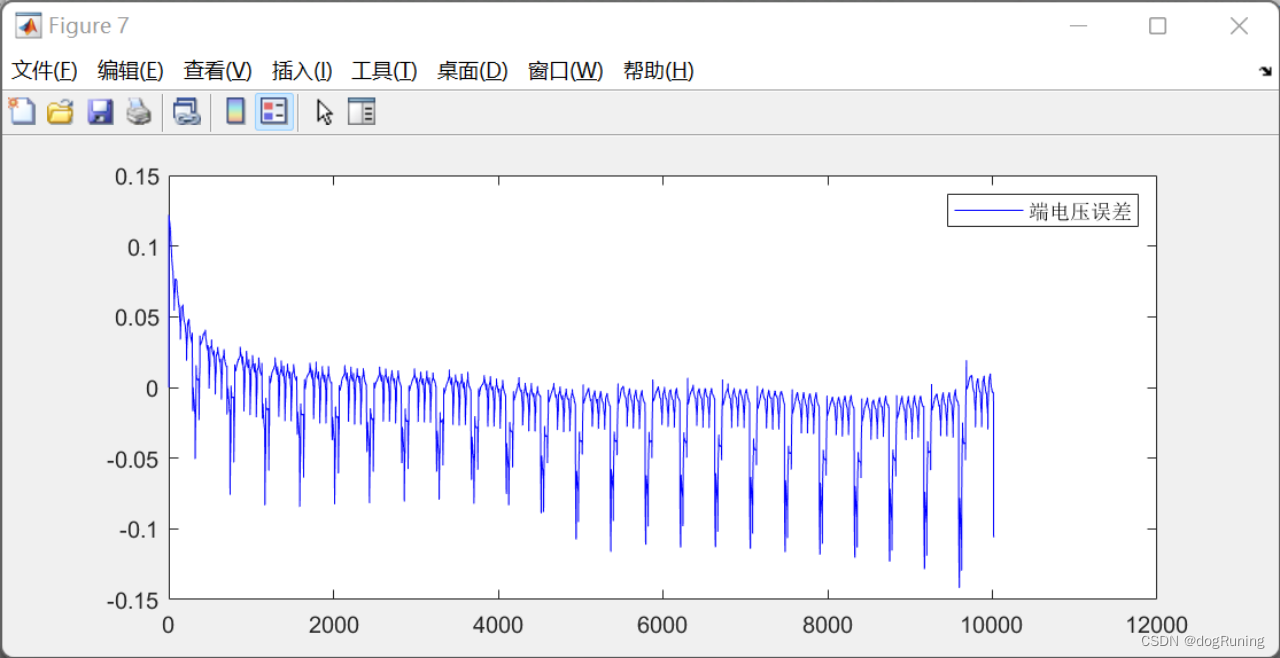
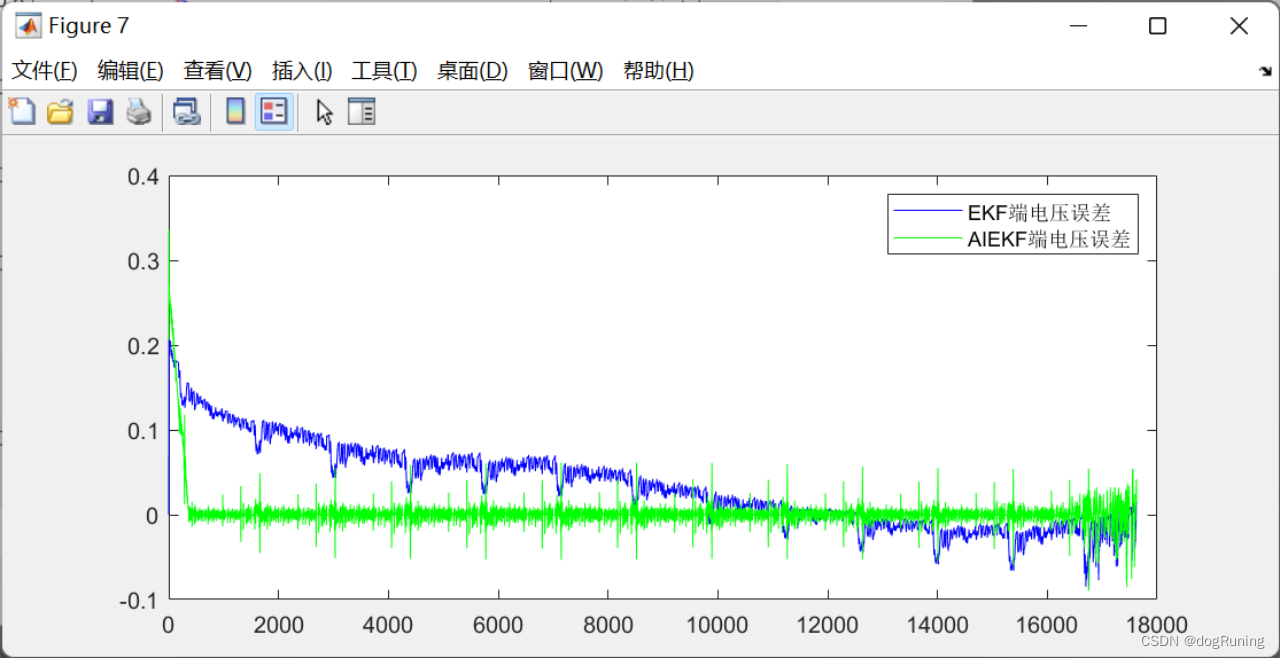
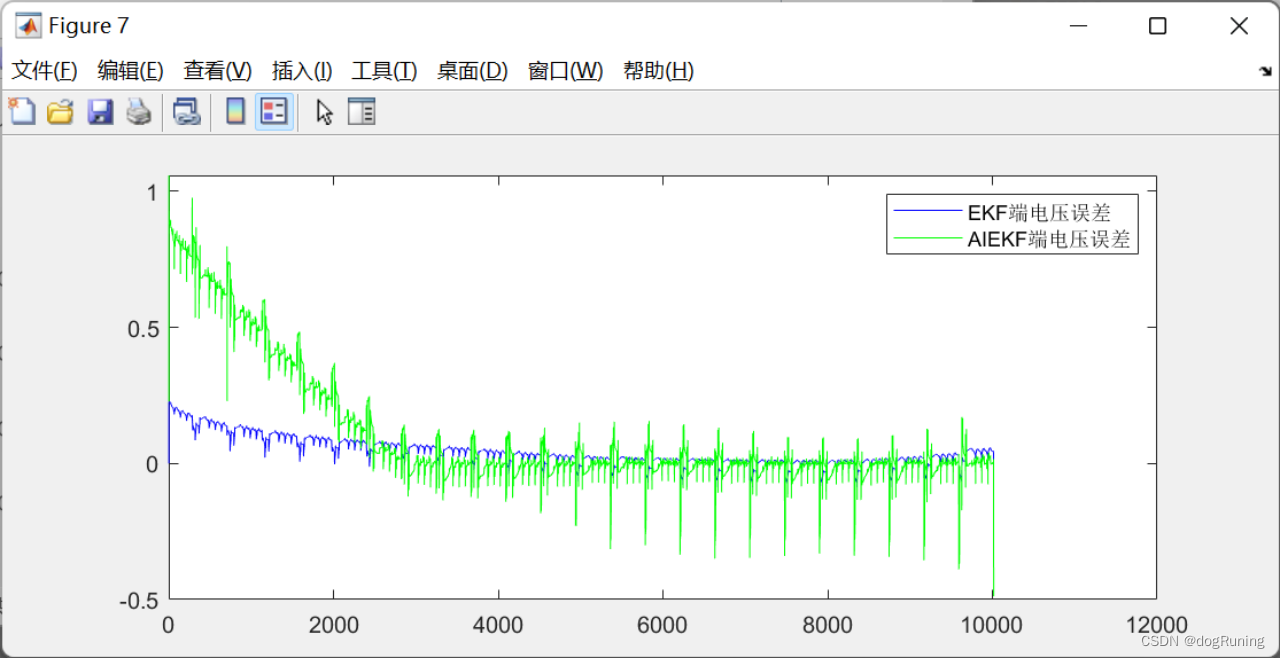
plot(t,error_V_EKF,'b',t,error_V_AIEKF,'g');
legend('EKF端电压误差','AIEKF端电压误差'); % SOC估计结果图
figure
hold on;box on;
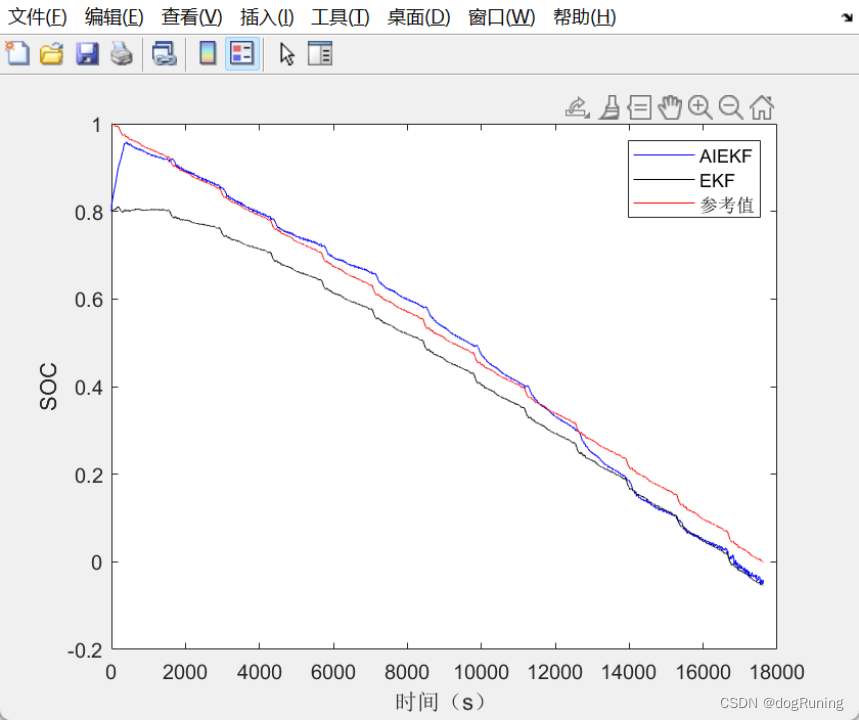
plot(SOC_aiekf,'b');%AIEKF
plot(SOC_ekf,'k'); %EKF
plot(soc_act,'r');
legend('AIEKF','EKF','参考值')
xlabel('时间(s)')
ylabel('SOC')
axis([0 12000 0 1])figure
hold on;box on;
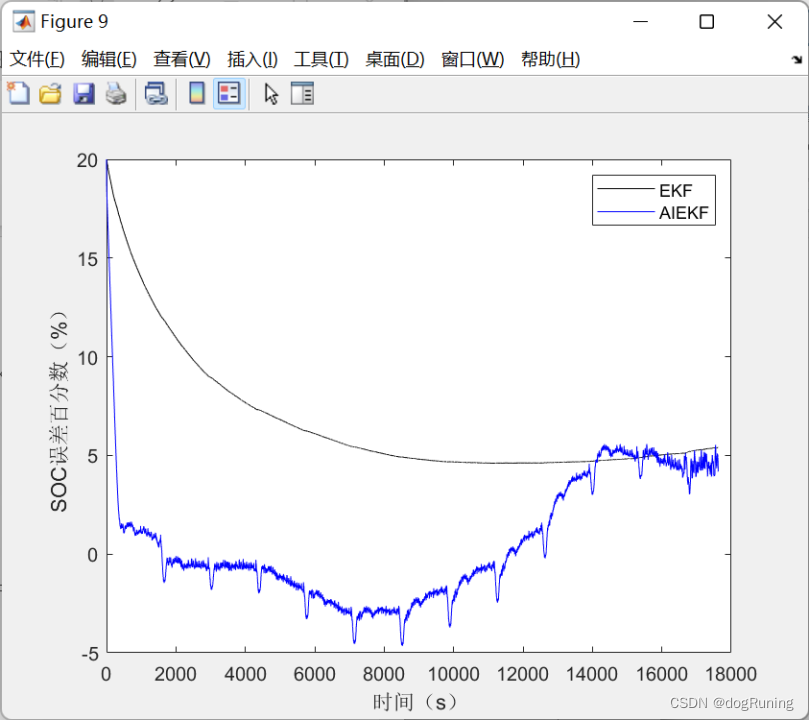
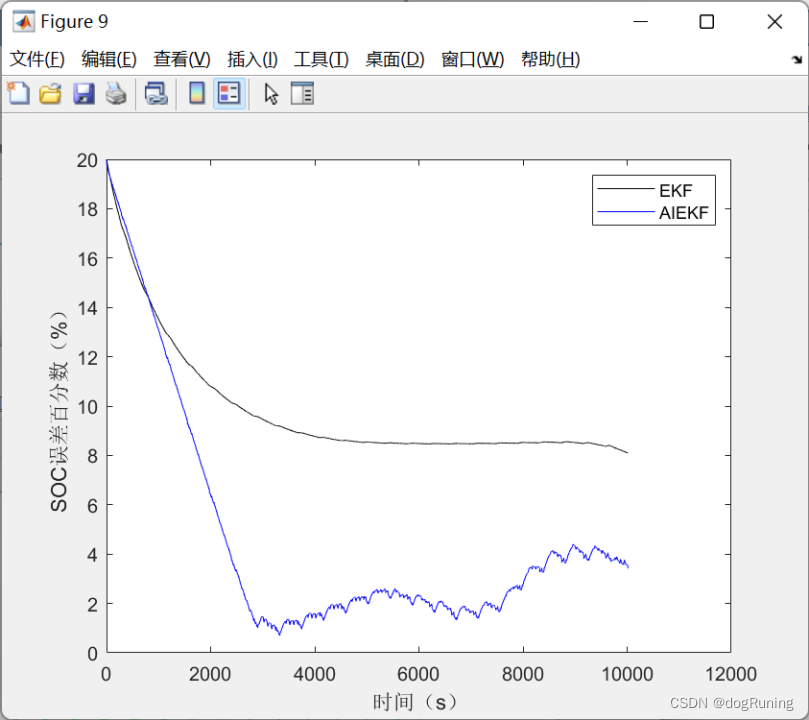
plot(100*error_SOC_EKF,'k');
plot(100*error_SOC_AIEKF,'b');
legend('EKF','AIEKF')
xlabel('时间(s)')
ylabel('SOC误差百分数(%)')
axis([0 12000 -10 15])
仿真结果
FUDS工况下参考SOC曲线
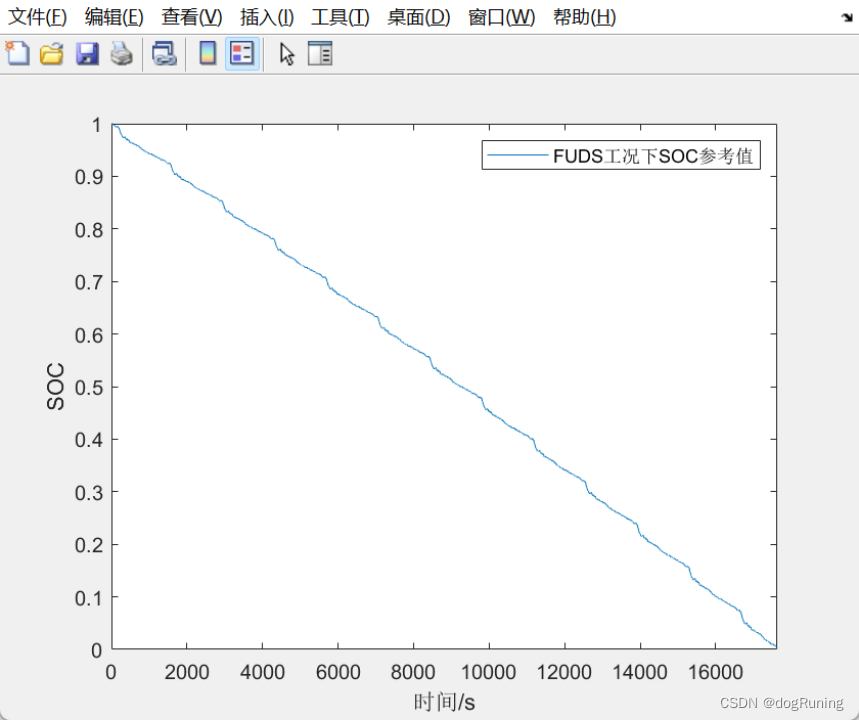
DST工况下参考SOC曲线
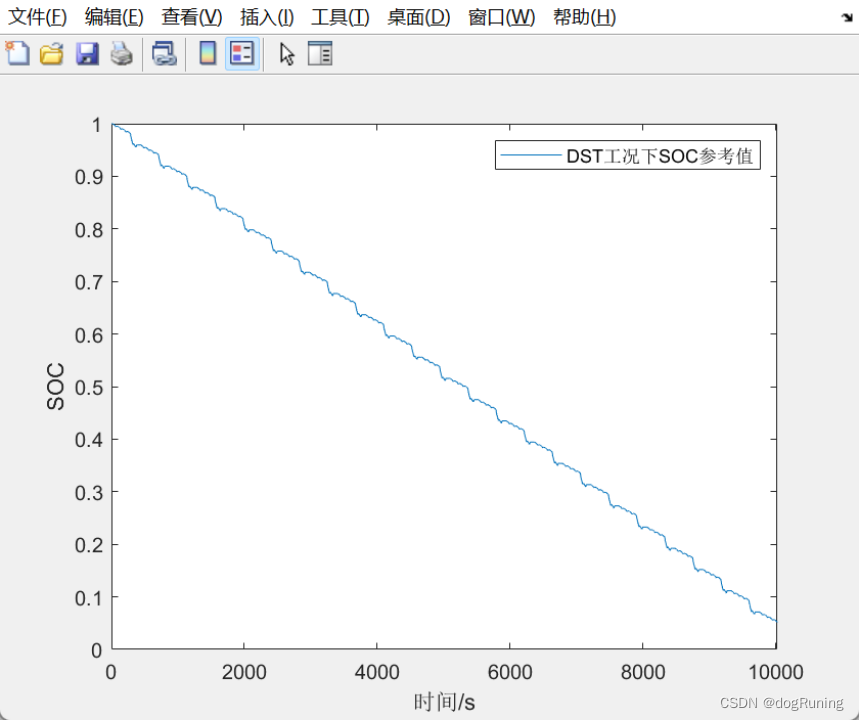
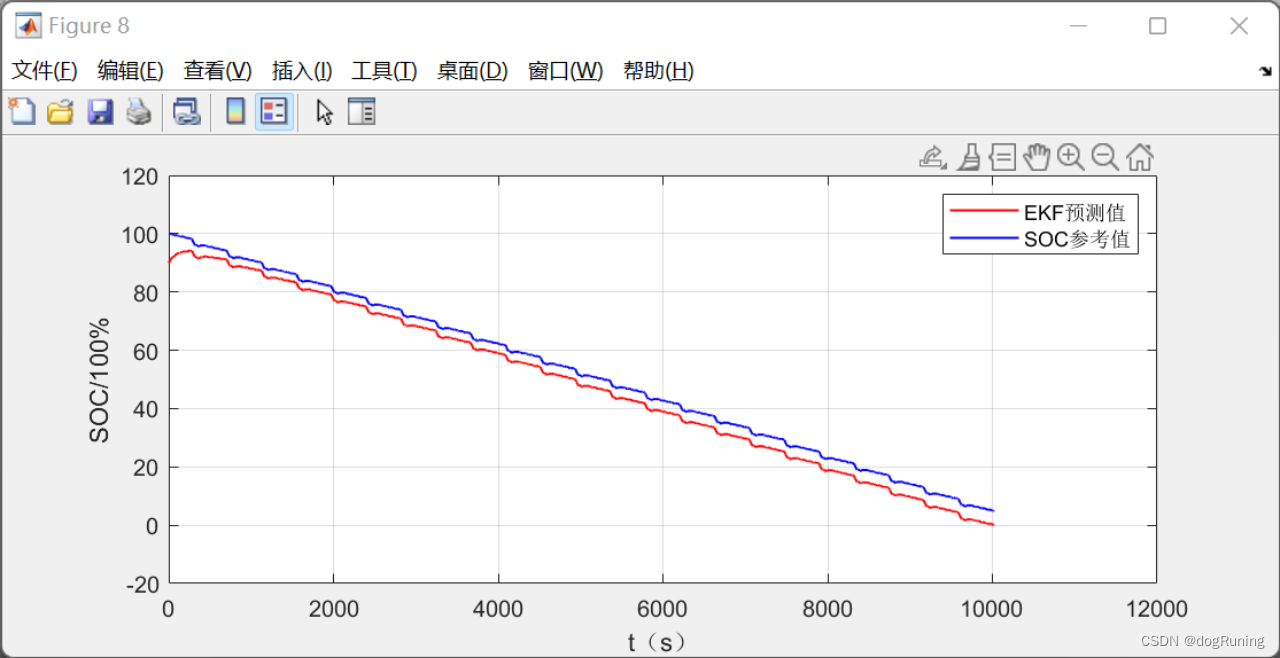
FUDS工况下SOC估计对比图(EKF与参考值)
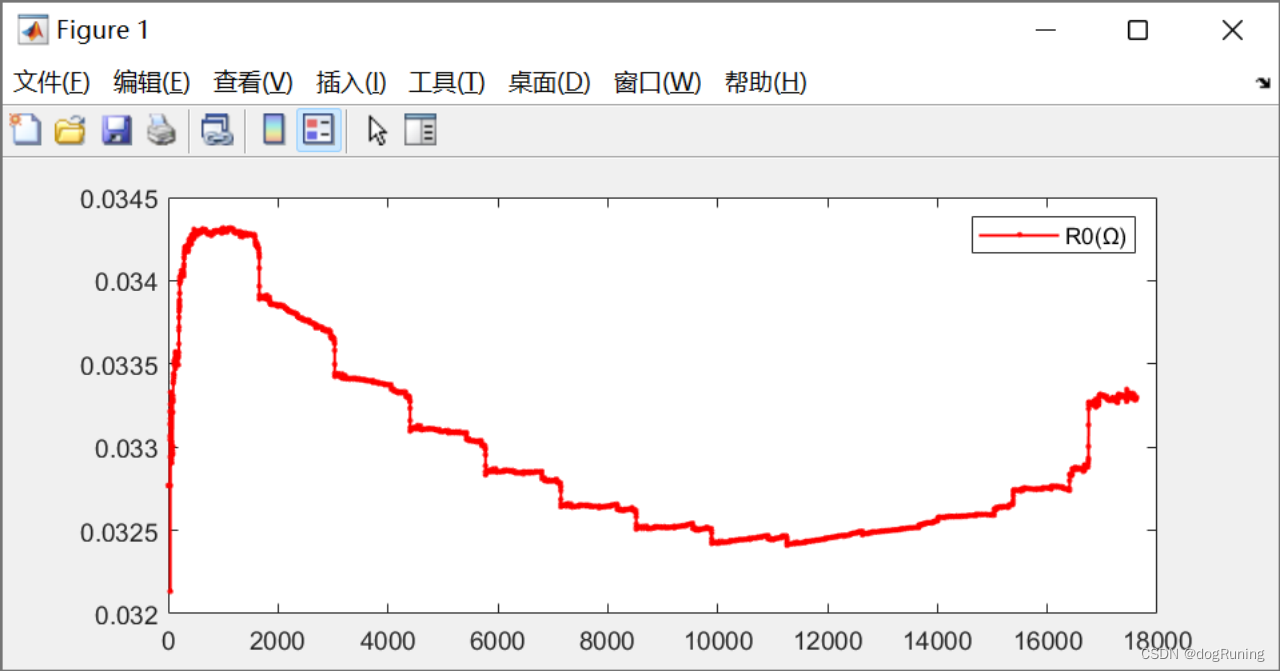
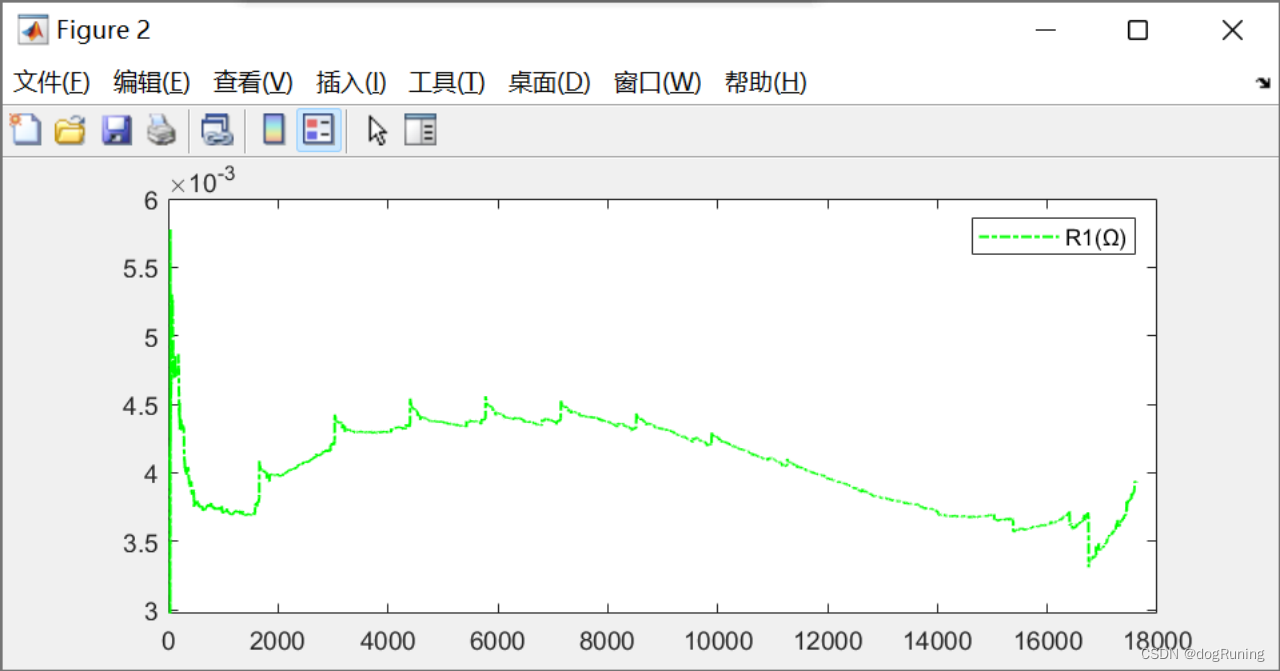

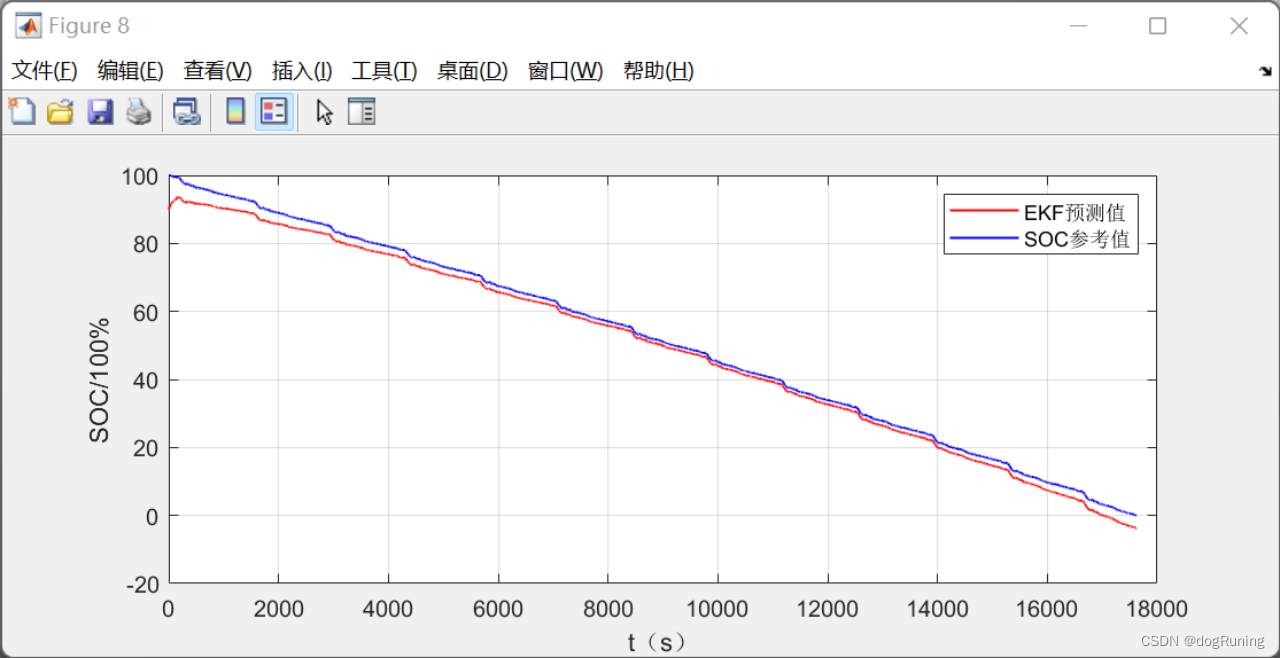
FUDS工况下SOC估算绝对误差曲线图
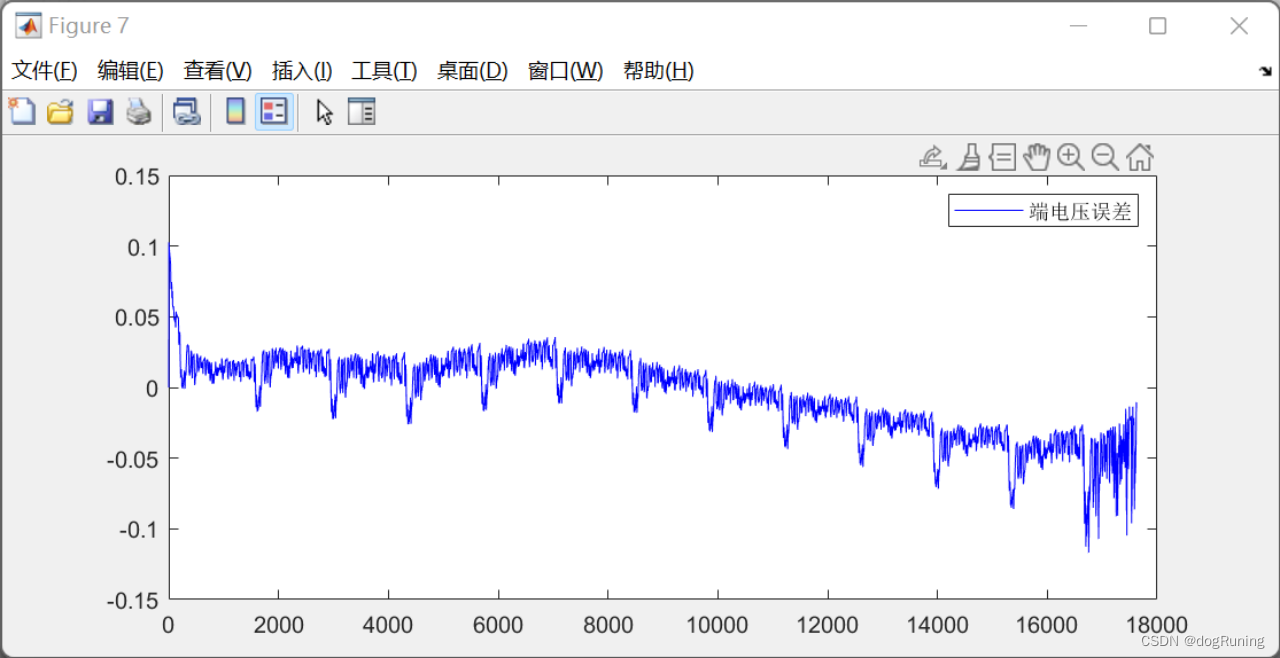

DST工况下SOC估计对比图(EKF与参考值)
DST工况下SOC估算绝对误差曲线图
FUDS工况下SOC估算曲线图(参考值 EKF AIEKF)

SOC估算不同算法绝对误差曲线图
DST工况下SOC估算曲线图(参考值 EKF AIEKF)

SOC估算不同算法绝对误差曲线图
相关文章:

自适应迭代扩展卡尔曼滤波算法AIEKF估计SOC VS 扩展卡尔曼估计SOC
自适应迭代扩展卡尔曼滤波算法(AIEK) 自适应迭代扩展卡尔曼滤波算法(AIEK)是一种滤波算法,其目的是通过迭代过程来逐渐适应不同的状态和环境,从而优化滤波效果。 该算法的基本思路是在每一步迭代过程中&a…...

2023-亲测有效-git clone失败怎么办?用代理?加git?
git 克隆不下来,超时 用以下格式: git clone https://ghproxy.com/https://github.com/Tencent/ncnn.git 你的网站前面加上 https://ghproxy.com/ 刷的一下就下完了!!...

An Empirical Study of GPT-3 for Few-Shot Knowledge-Based VQA
本文是LLM系列文章,针对《An Empirical Study of GPT-3 for Few-Shot Knowledge-Based VQA》的翻译。 GPT-3对基于小样本知识的VQA的实证研究 摘要引言相关工作方法OK-VQA上的实验VQAv2上的实验结论 摘要 基于知识的视觉问答(VQA)涉及回答需…...
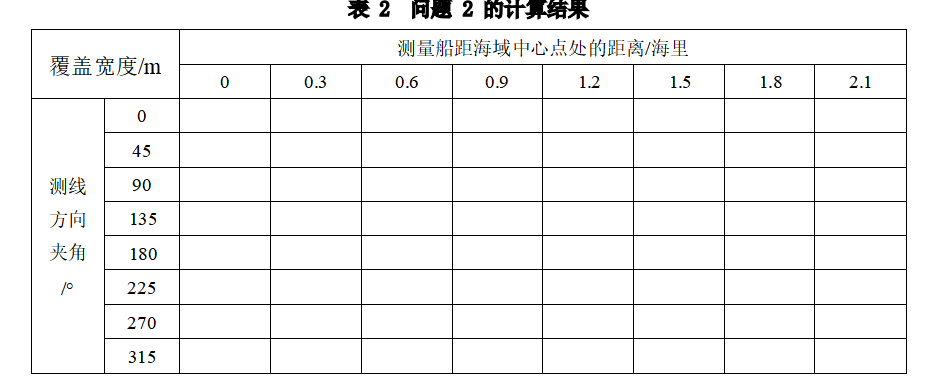
2023高教社杯数学建模B题思路分析 - 多波束测线问题
# 1 赛题 B 题 多波束测线问题 单波束测深是利用声波在水中的传播特性来测量水体深度的技术。声波在均匀介质中作匀 速直线传播, 在不同界面上产生反射, 利用这一原理,从测量船换能器垂直向海底发射声波信 号,并记录从声波发射到…...

02-docker network
Docker网络 Docker网络是什么 Docker 网络是 Docker 容器之间进行通信和连接的网络环境。在 Docker 中,每个容器都有自己的网络命名空间,这意味着每个容器都有自己的网络接口、IP 地址和网络配置 Docker网络启动后,会在宿主机中建立一个名…...

栈和队列经典笔试题
文章目录 栈和队列的回顾💻栈🩳队列👟 栈和队列经典笔试题🔋有效的括号🎸用队列实现栈 🕯用栈实现队列🔭设计循环队列🧼 安静的夜晚 你在想谁吗 栈和队列的回顾💻 栈&am…...

No5.9:多边形内角和公式
#!/usr/bin/python # -*- coding: UTF-8 -*-#指定了编码,中文就能正常展示 # codingutf-8def calc_degree(n):#n代表边形的总数degree (n - 2) * 180#多边形内角和公式return degreeprint(calc_degree(3))#三角形的内角和 print(calc_degree(4))#四边形的内角和【小…...
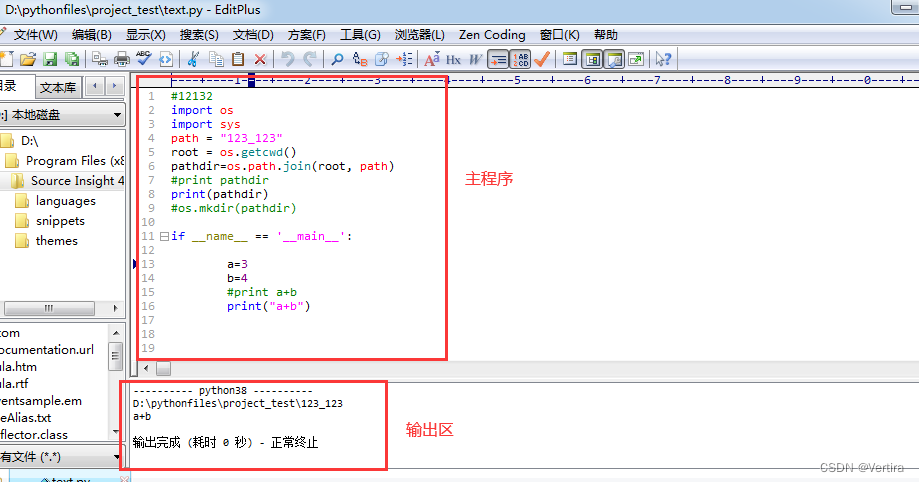
EditPlus 配置python 及Anaconda中的python
若不是pycharm vscode 太大,太占内存,谁会想到用Notepad,EdirPlus 配置python呢!!! 话不多说,首先你自己安装好EditPlus。开始 菜单栏 选择 工具 -> 配置自定义工具 组名:python 命令:d:\*…...

linux 编译 llvm + clang
1. 需要下载以下三个压缩包,下载源码:Release LLVM 15.0.7 llvm/llvm-project GitHub clang-15.0.7.src.tar.xzcmake-15.0.7.src.tar.xzllvm-15.0.7.src.tar.xz 2. 解压后将 clang 源码放入 llvm/tools/ 下 3. 将解压后的 cmake-15.0.7…...
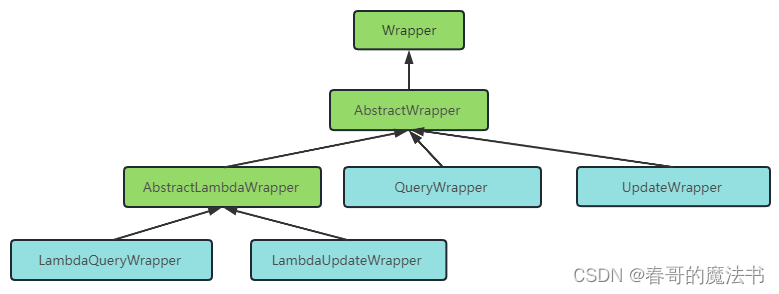
Mybatis 框架 ( 四 ) QueryWrapper
4.5.Wrapper条件构造器 Wrapper : 条件构造抽象类,最顶端父类 AbstractWrapper : 用于查询条件封装,生成 sql 的 where 条件 QueryWrapper : Entity 对象封装操作类,不是用lambda语法 UpdateWrapper &am…...

数据结构和算法之二分法查找
二分法查找,也称作二分查找或折半查找,是一种在有序数组中快速查找特定元素的算法。它采用分治法思想,通过将问题划分为规模更小的子问题,并且通过对子问题的查找来解决原问题。 二分法查找的思路是不断地将数组一分为二…...

系统日期如何在页面展示,框架是react或者vue3
安装插件dayjs或者moment.js 2.使用setInterval(useInterval)或者requestAnimationFrame react项目中useInterval的代码示例: import React, {useState } from react; import { useInterval } from "ahooks"; import moment fro…...

(二十二)大数据实战——Flume数据采集之故障转移案例实战
前言 本节内容我们完成Flume数据采集的故障转移案例,使用三台服务器,一台服务器负责采集nc数据,通过使用failover模式的Sink处理器完成监控数据的故障转移,使用Avro的方式完成flume之间采集数据的传输。整体架构如下:…...

前端小案例3:Flex弹性布局行内元素宽度自适应
前端小案例3:Flex弹性布局行内元素宽度自适应 项目背景:需要在一行上展示空调设备的三个模式(制冷、制热、通风)或者两个模式(制冷、制热);因为不同产品的模式数量不同,因此需要让模…...

纳尼?小说还要用看的?这可以听!无广!
这是一款听书软件,可以自定义书源,自己设置书架,页面简单易操作,无广告。 支持直接搜索书名,链接,图文,本地文件等方式听书 拥有30多主播声音,分类细致 支持倍速、添加BGM等...

【微服务部署】四、Jenkins一键打包部署NodeJS(Vue)前端项目步骤详解
本文介绍使用Jenkins一键将NodeJS(Vue)前端项目打包并上传到生产环境服务器,这里使用的是直接打包静态页面,发送到远程服务器Nginx配置目录的方式,首先确保服务器环境配置好,安装Nginx,运行目录…...
【前端】禁止别人调试自己的前端页面代码
无限debugger 前端页面防止调试的方法主要是通过不断 debugger 来疯狂输出断点,因为 debugger 在控制台被打开的时候就会执行由于程序被 debugger 阻止,所以无法进行断点调试,所以网页的请求也是看不到的代码如下: /** * 基础禁止…...

UDP的可靠性传输
UDP系列文章目录 第一章 UDP的可靠性传输-理论篇(一) 第二章 UDP的可靠性传输-理论篇(二) 文章目录 UDP系列文章目录前言1.TCP 和UDP格式对比2.UDP分片原理3.UDP 传输层应该注意问题4.MTU5.UDP 分片机制设计重点 一、ARQ协议什么…...

科研笔记:TPAMI submission guideline
1 author information Author Information - IEEE Transactions on Pattern Analysis and Machine Intelligence | IEEE Computer Society Digital Library 1.1 会议期刊extension 当一个TPAMI的提交基于之前的会议论文时,IEEE要求期刊论文是之前出版物的“实质…...
:打开文件、读文件、关闭文件)
Python文件操作(02):打开文件、读文件、关闭文件
一、读文本文件 打开文件读文件内容关闭文件 1、在读取文件内容后进行解码操作 """ 1. 打开文件- 路径:相对路径:当前项目(读文件.py)所在的目录下查找需要读取的文件绝对路径:文件--右键--Copy Pat…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
