管理类联考——数学——汇总篇——知识点突破——应用题——最值问题
⛲️
一、考点讲解
最值问题是应用题中最难的题目,也是考生普遍丢分的题目。最值问题一般要结合函数来分析,一般结合二次函数和平均值定理求解。最值问题的求解步骤是:先设未知变量,然后根据题目建立函数表达式,最后利用函数的特征求解最值。
二、考试解读
- 应用题的最值问题难度较大,而且计算量也略大,对于基础一般的考生,建议在考试中最后再做。
- 熟练掌握二次函数和平均值定理是求解最值问题的关键。
- 函数关系的建立是解题核心,所以要准确理解题意,建立函数表达式。
- 考试频率级别:中。
三、命题方向
-
二次函数求最值
思路:如果出现二次函数,采用抛物线分析求解。 -
均值定理求最值
思路:应用平均值定理分析,当和为定值时,乘积有最大值;当积为定值时,和有最小值,对于两个正数,也可记住公式: a + b ≥ 2 a b a+b≥2\sqrt{ab} a+b≥2ab。
最值问题是应用题中最难的题目,也是考生普遍丢分的题目。最值问题一般要结合函数来分析,一般结合二次函数和平均值定理求解。
最值问题的求解步骤是:先设未知变量,然后根据题目建立函数表达式,接着利用函数的特征求解最值。
🌊
应用题与二次函数的综合求最值问题:主要利用二次函数的顶点公式求解,较为简单,注意定义域即可。
这种题目的出题模式非常固定:即这种题目通常以利润问题出现,然后问我们利润的取得最值时售价为多少。
出题模式很固定:
A.商品每上涨n元,少卖m件;
B.商品每下降n元,多卖m件;
固定解题思路:设上涨/下降x个n元。
🐟
| 模型识别 | 解题方法 | 备注 |
|---|---|---|
| 转化为一元二次函数求最值 | 列出符合题干的一元二次函数表达式,要注意对称轴是不是落在定义域内 | |
| 转化为均值不等式求最值 | 使用均值不等式的口诀“一正二定三相等” | |
| 至多至少问题 | 常用极值法(如一个极大,其余极小;或者一个极小,其余极大) |
🐟
1.转化为一元二次函数求最值
解题方法
根据应用题的已知条件,设未知数,列出符合题干的一元二次函数的表达式,要注意对称轴是不是落在定义域内。
2.转化为均值不等式求最值
解题方法
如果题干中已知条件为和的定值,求积的最大值;或者已知条件为积的定值,求和的最小值,则一般考查均值不等式.使用均值不等式的口诀“一正二定三相等”。
3.转化为不等式求最值
4.至多至少问题
解题方法
至多至少问题,常用极值法(如一个极大,其余极小;或者一个极小,其余极大)。

相关文章:

管理类联考——数学——汇总篇——知识点突破——应用题——最值问题
⛲️ 一、考点讲解 最值问题是应用题中最难的题目,也是考生普遍丢分的题目。最值问题一般要结合函数来分析,一般结合二次函数和平均值定理求解。最值问题的求解步骤是:先设未知变量,然后根据题目建立函数表达式,最后利…...

学习SpringMvc第二战之【SpringMVC之综合案例】
目录 一. 参数传递 1.前期准备工作(替换pom.xml中的部分依赖) 1.1将log4j替换成为slf4j(将打印语句替换成为日志文件输出结果) 2.正式操作 1.基础传参 1.1创建方法,用于验证传参 1.2构建界面回显 1.3设置访问路径(localho…...
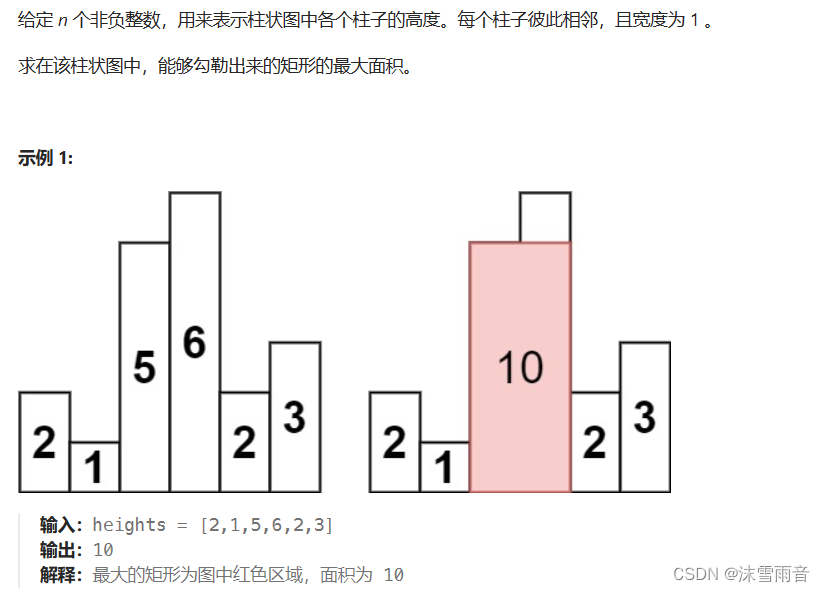
【算法日志】单调栈: 单调栈简介及其应用
代码随想录刷题60Day 目录 单调栈简介 单调栈的应用 下次更高温 下一个更大元素1 下一个更大元素2 接雨水 柱状图中最大矩形 单调栈简介 单调栈(Monotonic Stack)是一种特殊的栈数据结构,它满足元素的单调性,这种单调性需…...
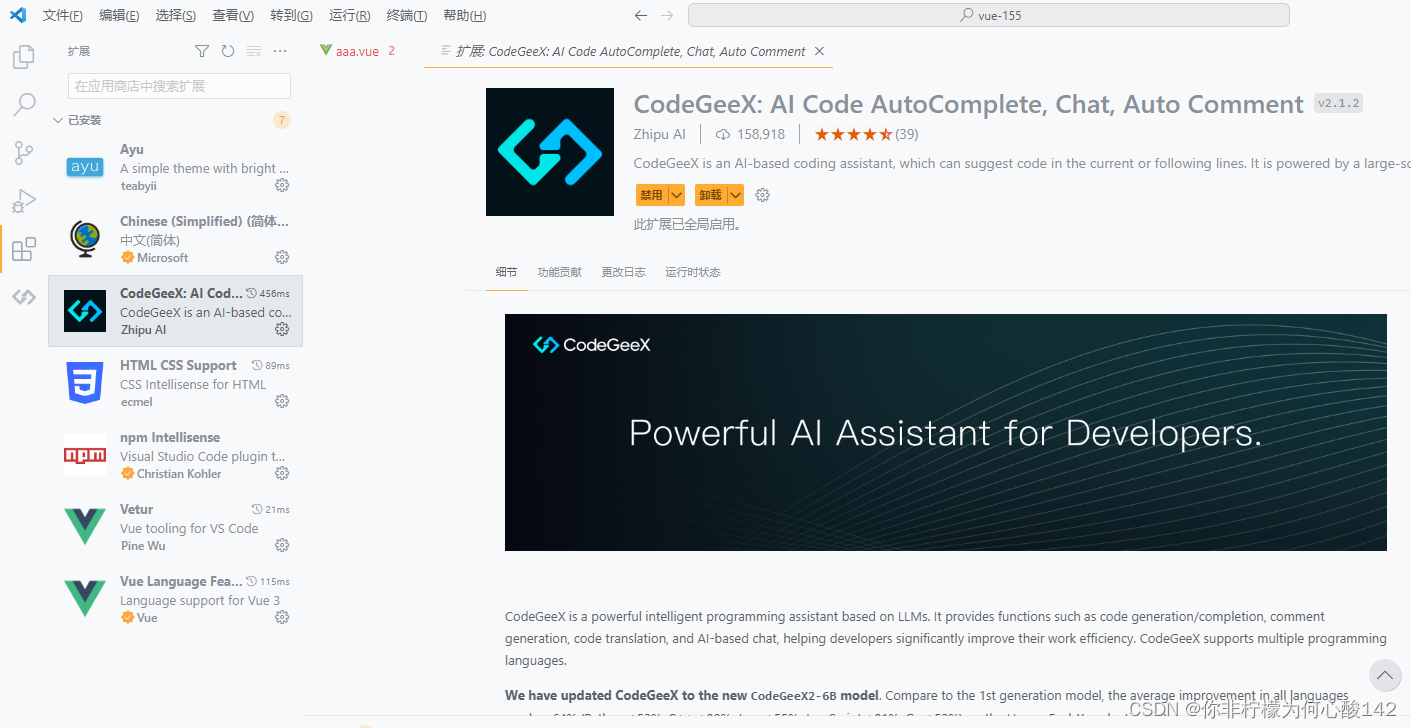
VSCode自动分析代码的插件
今天来给大伙介绍一款非常好用的插件,它能够自动分析代码,并帮你完成代码的编写 效果如下图 首先我们用的是VSCode,(免费随便下) 找到扩展,搜索CodeGeeX,将它下载好,就可以实现了 到…...
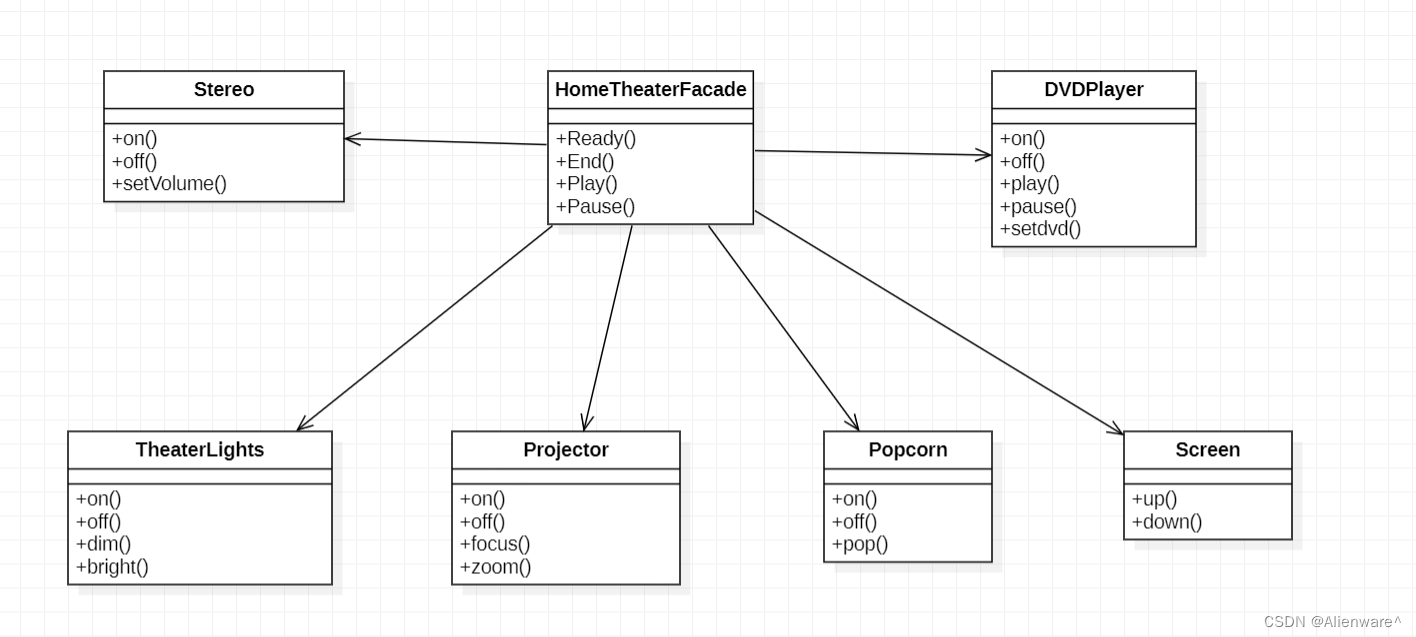
设计模式之外观模式
文章目录 影院管理项目传统方式解决影院管理传统方式解决影院管理问题分析外观模式基本介绍外观模式原理类图外观模式解决影院管理传统方式解决影院管理说明外观模式应用实例 外观模式的注意事项和细节 影院管理项目 组建一个家庭影院: DVD 播放器、投影仪、自动屏…...

Web端测试和 App端测试有何不同?
Web 端测试和 App 端测试是针对不同平台的上的应用进行测试,Web应用和App端的应用实现方式不同,测试时的侧重点也不一样。 今天这篇文章就来介绍下两者的不同之处以及测试时的侧重点。 同时,我也准备了一份软件测试面试视频教程(…...
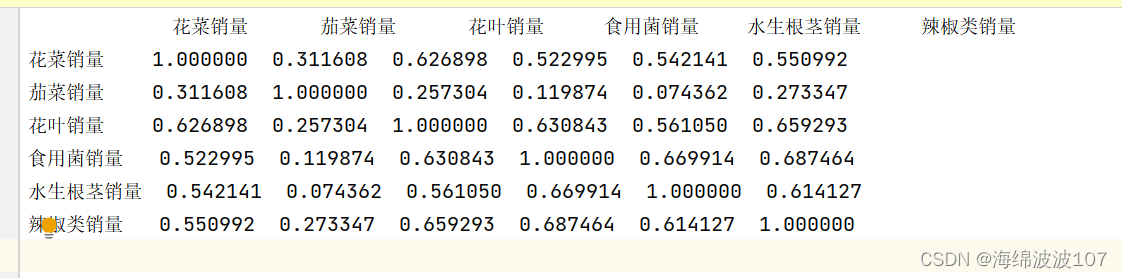
12.(Python数模)(相关性分析一)相关系数矩阵
相关系数矩阵 相关系数矩阵是用于衡量多个变量之间关系强度和方向的统计工具。它是一个对称矩阵,其中每个元素表示对应变量之间的相关系数。 要计算相关系数矩阵,首先需要计算每对变量之间的相关系数。常用的相关系数包括皮尔逊相关系数和斯皮尔曼相关…...

系统架构设计师(第二版)学习笔记----嵌入式系统及软件
【原文链接】系统架构设计师(第二版)学习笔记----嵌入式系统及软件 文章目录 一、嵌入式系统1.1 嵌入式系统的组成1.2 嵌入式系统的特点1.3 嵌入式系统的分类 二、嵌入式软件2.1 嵌入式系统软件分层2.2 嵌入式软件的主要特点 三、安全攸关软件的安全性设…...

Python列表操作指南:索引、切片、遍历与综合应用
文章目录 列表简介创建列表索引和切片列表的长度列表的拼接和重复检查元素是否存在列表的方法index() 方法count() 方法 列表的修改和删除修改元素删除元素列表的排序和反转添加元素 列表的拷贝列表的遍历列表的切片列表的嵌套列表推导式 python精品专栏推荐python基础知识&…...

第15章_锁: MySQL并发访问相同记录以及从数据操作的类型划分锁(读锁、写锁)
事务的 隔离性 由这章讲述的 锁 来实现。 1. 概述 锁是计算机协调多个进程或线程并发访问某一资源的机制. 在程序开发中会存在多线程同步的问题, 当多个线程并发访问某个数据的时候, 尤其是针对一些敏感数据(订单, 金额), 我们就需要保证这个数据在任何时刻最多只有一个线…...

PHP 排序函数使用方法,按照字母排序等操作
详解PHP排序方法使用 一、sort() 函数 用于对数组单元从低到高进行排序。 //数组 $data array(D,F,A,C,B); //排序 sort($data); //输出排版标签 echo "<pre>"; //打印数据 print_r($data);die;输出结果: 二、rsort() 函数 用于对数组单元从高到…...

windows本地验证码识别工具
windows本地验证码识别小工具 - 可以用在windows系统中,并可以集成在Java或python程序中 演示视频如下:可用于识别4-7位的字母数字组合的验证码(识别准确率在70% - 80%)。 验证码识别演示 本项目未开源,如需使用请联…...
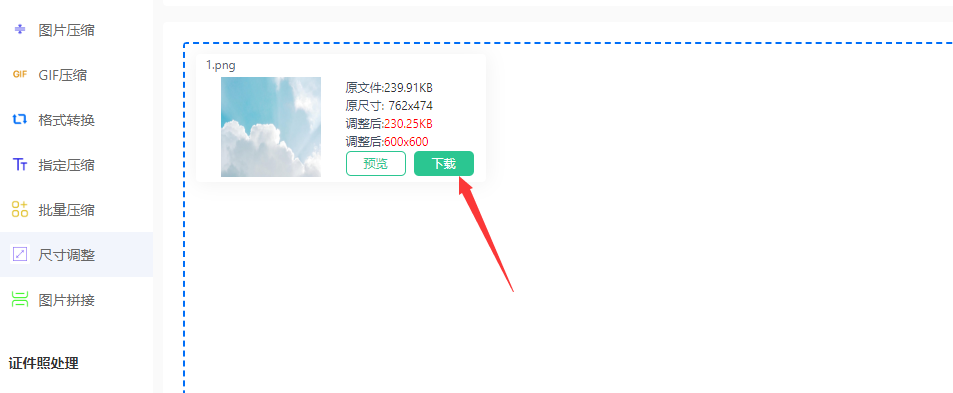
修改图片尺寸的几个简单方法
修改图片尺寸的几个简单方法~~图片,是我们常用的文件格式,也是日常生活与工作中重要的文件。图片记录了非常多的元素和内容,其中不乏有工作上的内容,也有对一些日常生活的记录。所以说,图片文件对我们来说是非常重要的…...

三、GoLang字符串的基本操作
一、转义符是什么? 转义字符意义\n换行,将当前位置移动到下一行开头\r回车,将当前位置移到本行开头\t相当于一个Tab键\\代表一个反斜线“\”\"代表一个双引号字符 代码实战 package mainimport "fmt"/* *字符串基本用法 */ func main…...
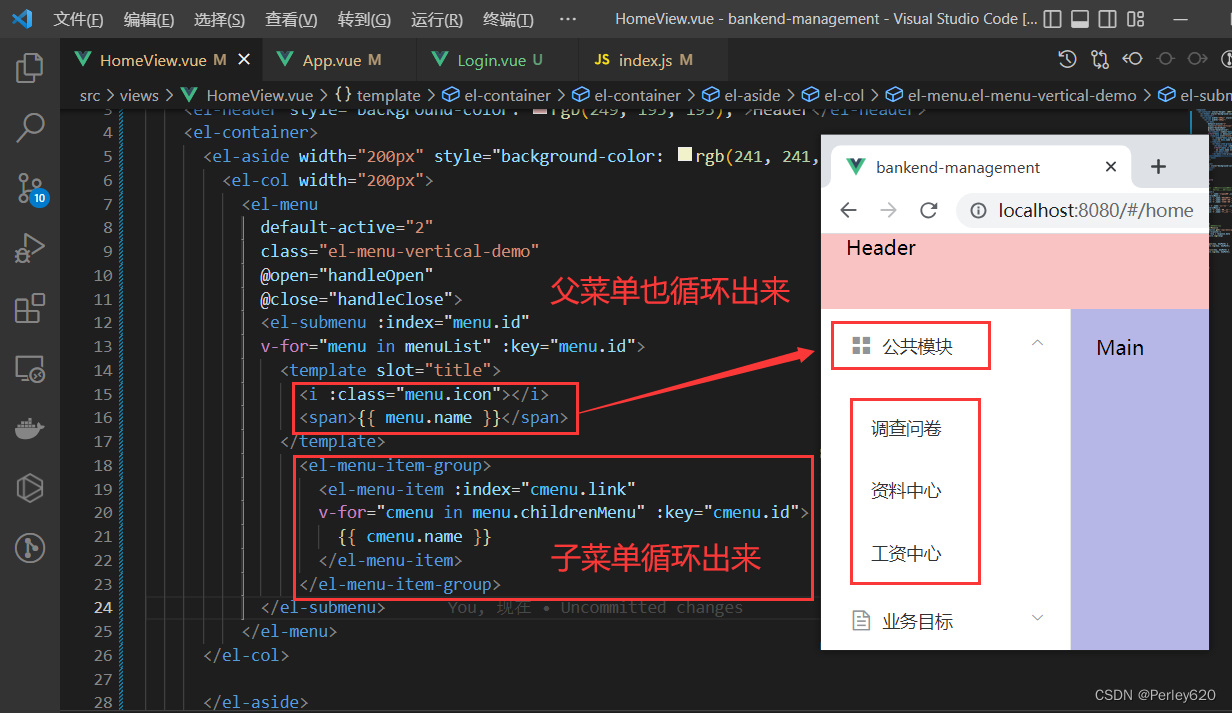
基于vue-cli创建后台管理系统前端页面——element-ui,axios,跨域配置,布局初步,导航栏
目录 引出安装npm install安装element-ui安装axios 进行配置main.js中引入添加jwt前端跨域配置 进行初始布局HomeView.vueApp.vue 新增页面和引入home页面导航栏总结 引出 1.vue-cli创建前端工程,安装element-ui,axios和配置; 2.前端跨域的配…...

在 ubuntu20.04 上安装 Pytorch
参考资料:https://www.linode.com/docs/guides/pytorch-installation-ubuntu-2004/ sudo apt update sudo apt install nvidia-cuda-toolkit (3G) mkdir anaconda cd ~/anaconda wget https://repo.anaconda.com/archive/Anaconda3-2020.11-Linux-x86_64.sh chmod …...
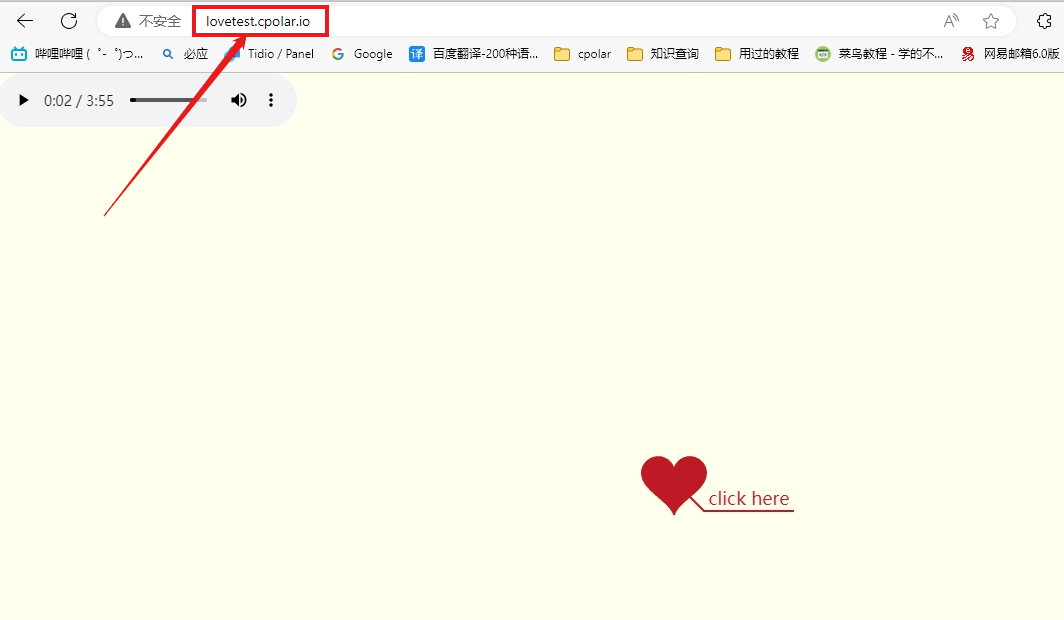
远程恋爱网站部署秘籍——群晖虚拟机助ni秀恩爱
文章目录 前言1. 安装网页运行环境1.1 安装php1.2 安装webstation 2. 下载网页源码文件2.1 访问网站地址并下载压缩包2.2 解压并上传至群辉NAS 3. 配置webstation3.1 配置网页服务3.2 配置网络门户 4. 局域网访问静态网页配置成功5. 使用cpolar发布静态网页,实现公网…...

vscode c++解决包含头文件红色波浪线问题
安装c/c插件后,按ctrlshiftp, 点击打开了c_cpp_properties.json文件,对其中的IncludePath进行编辑,示例如下: "includePath": ["${workspaceFolder}/**","${workspaceFolder}/include/**&q…...

PostgreSQL docker compose安装配置
docker-compose.yml如下: version: 3services:postgres:image: postgres:15.4healthcheck:test: [ "CMD", "pg_isready", "-q", "-d", "postgres", "-U", "root" ]timeout: 45sinterval: 1…...
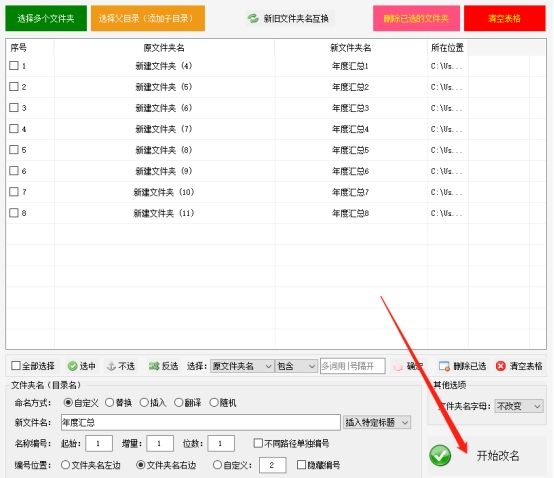
电脑文件批量重命名:高效操作技巧
随着时间的推移,我们积累的文件和文件夹数量越来越多,需要对它们进行合理的命名和管理,以便更方便地查找和利用。而文件批量重命名功能可以帮助我们更高效地管理文件夹。下面介绍五种方式,帮助你更好地利用文件批量重命名工具&…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...
