数据结构——七大排序[源码+动图+性能测试]

本章代码gitee仓库:排序
文章目录
- 🎃0. 思维导图
- 🧨1. 插入排序
- ✨1.1 直接插入排序
- ✨1.2 希尔排序
- 🎊2. 选择排序
- 🎋2.1 直接选择排序
- 🎋2.2 堆排序
- 🎏3. 交换排序
- 🎐3.1 冒泡排序
- 🎐3.2 快速排序
- 🎑hoare版本
- 🎑挖坑法
- 🎑前后指针
- 🎑小区间优化
- 🎑非递归
- 🎀4. 归并排序
- 🎁4.1 递归
- 🎁4.2 非递归
- 🎫5. 性能测试
- 🎖5.1 1w数据
- 🎖5.2 10w数据
- 🎖5.3 100w数据
- 🎖5.4 1000w数据
- 🎖5.5 1亿数据
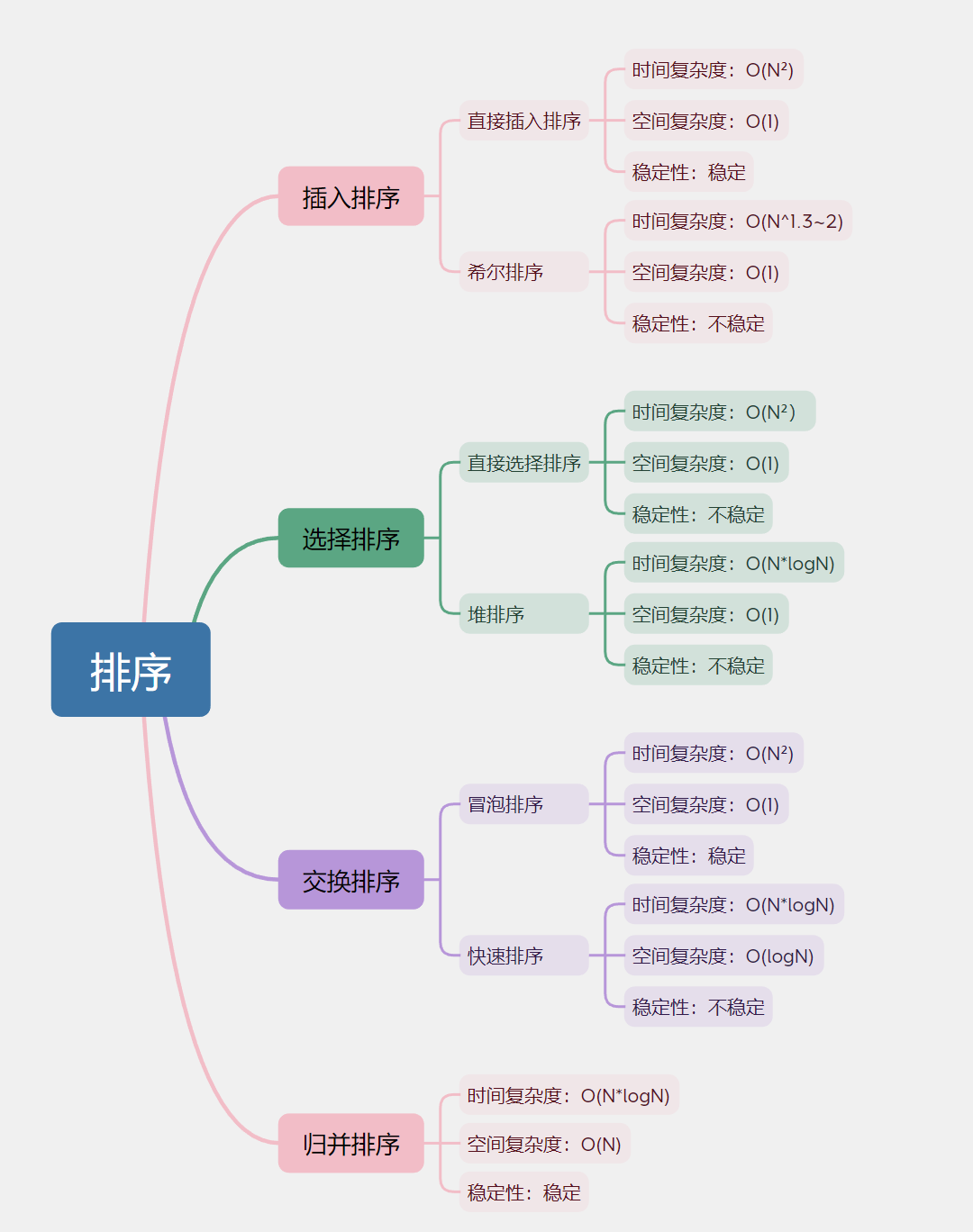
🎃0. 思维导图
🧨1. 插入排序
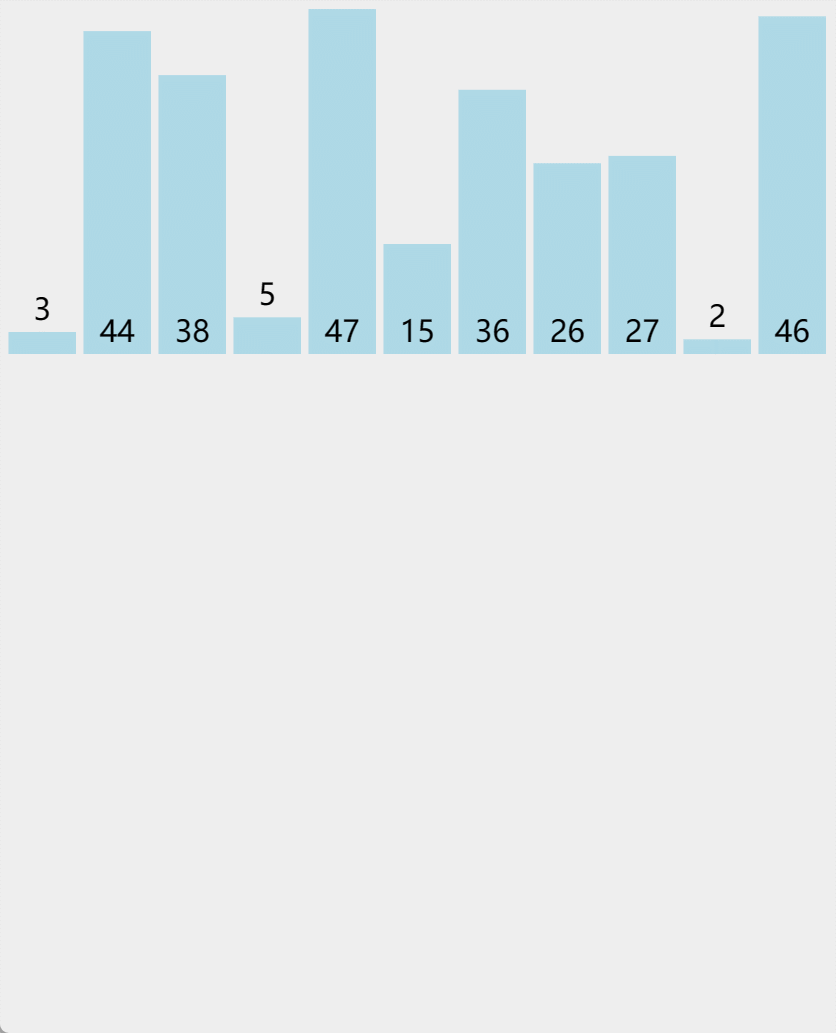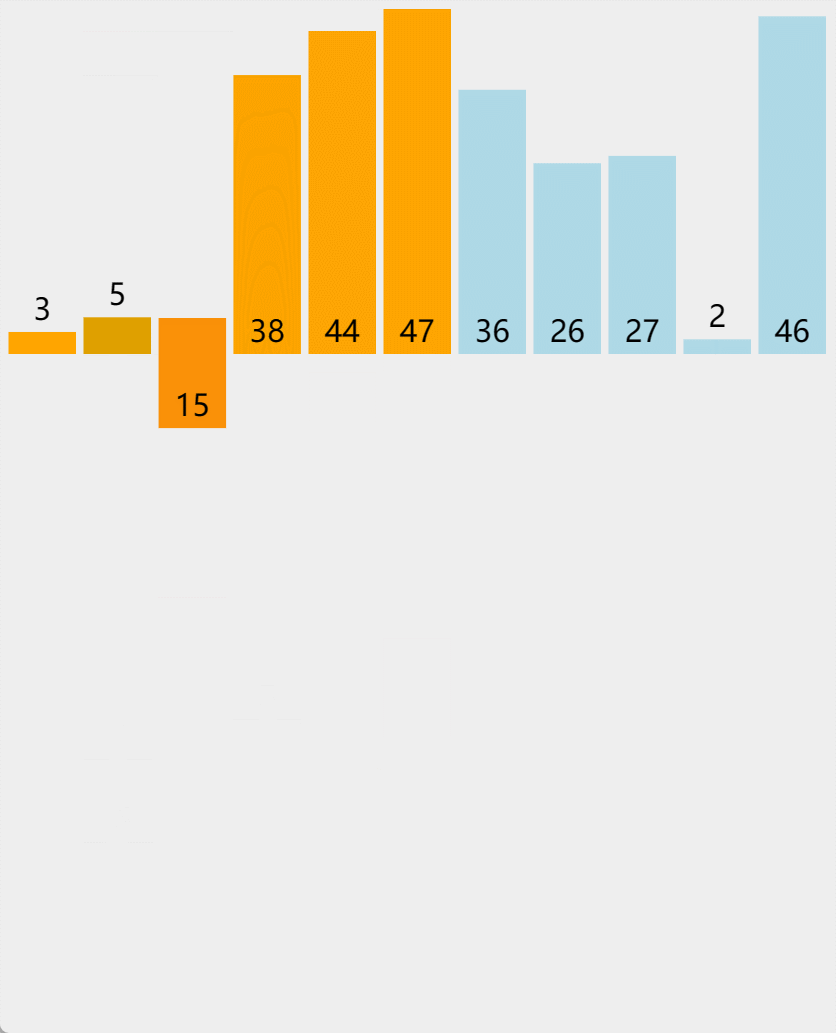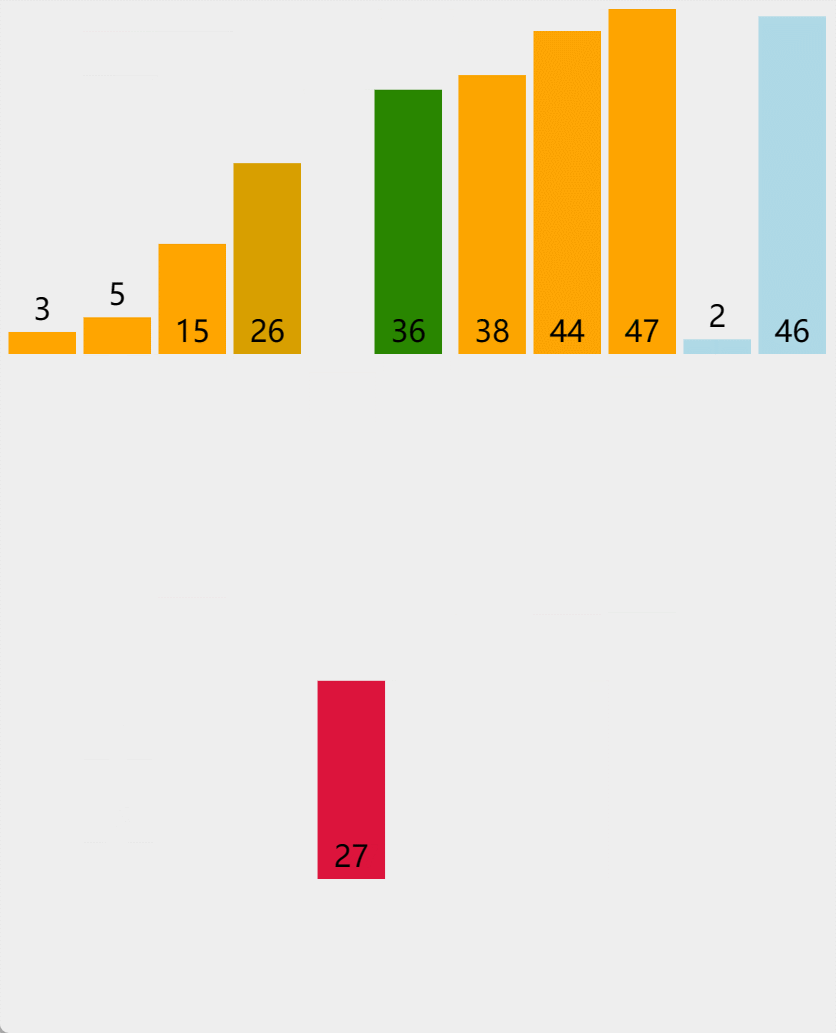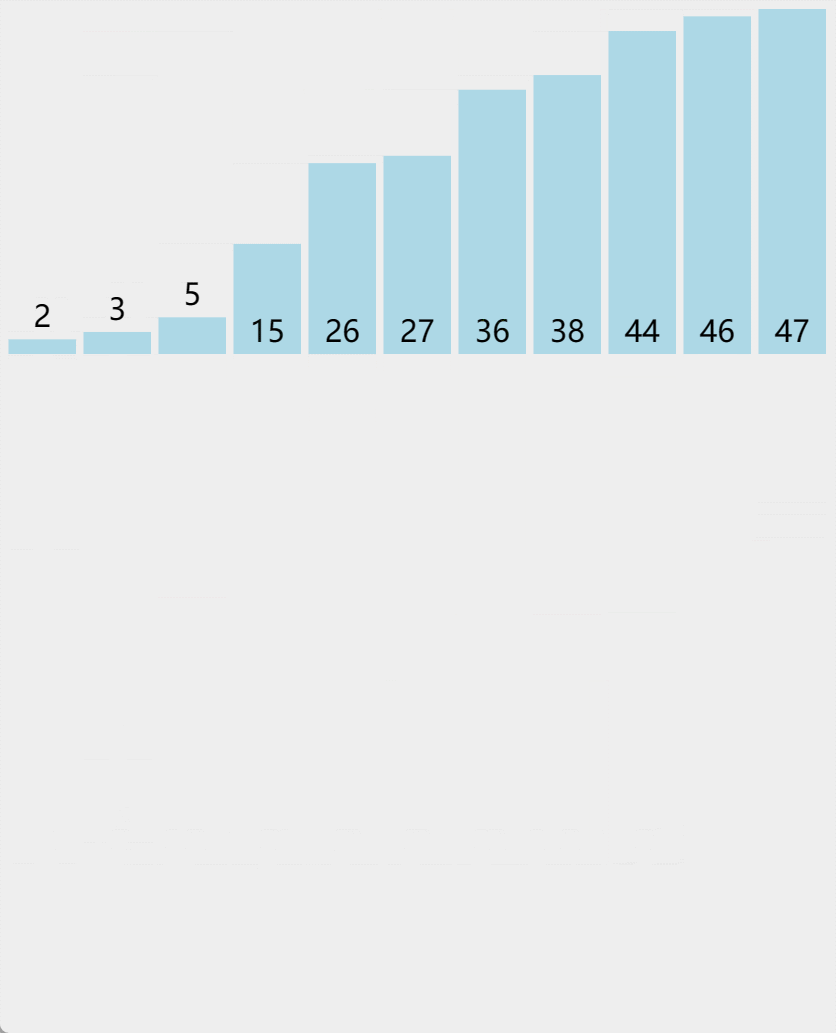
✨1.1 直接插入排序
我们日常打扑克牌,摸牌,让后将牌按顺序插入好,这其实就是插入排序的过程,打小插入排序的思想就植入我们的脑海
第一张牌不用管,直接拿在手里,之后的牌按照大小再一个一个插入即可
//直接插入排序
void InsertSort(int* a, int n)
{//第一张牌不用排,所以直接从下标1开始走for (int i = 1; i < n; i++){int end = i - 1;int tmp = a[i];while (end >= 0){if (a[end] > tmp){//往后挪数据a[end + 1] = a[end];end--;}elsebreak;}//直接break出来 或者 end = -1a[end + 1] = tmp;}
}
直接插入排序特性:
越接近有序,效率越高(不用那么多次挪动数据)
时间复杂度:O(N2)
逆序最坏O(N2),有序最好O(N)
空间复杂度:O(1)
稳定性:稳定
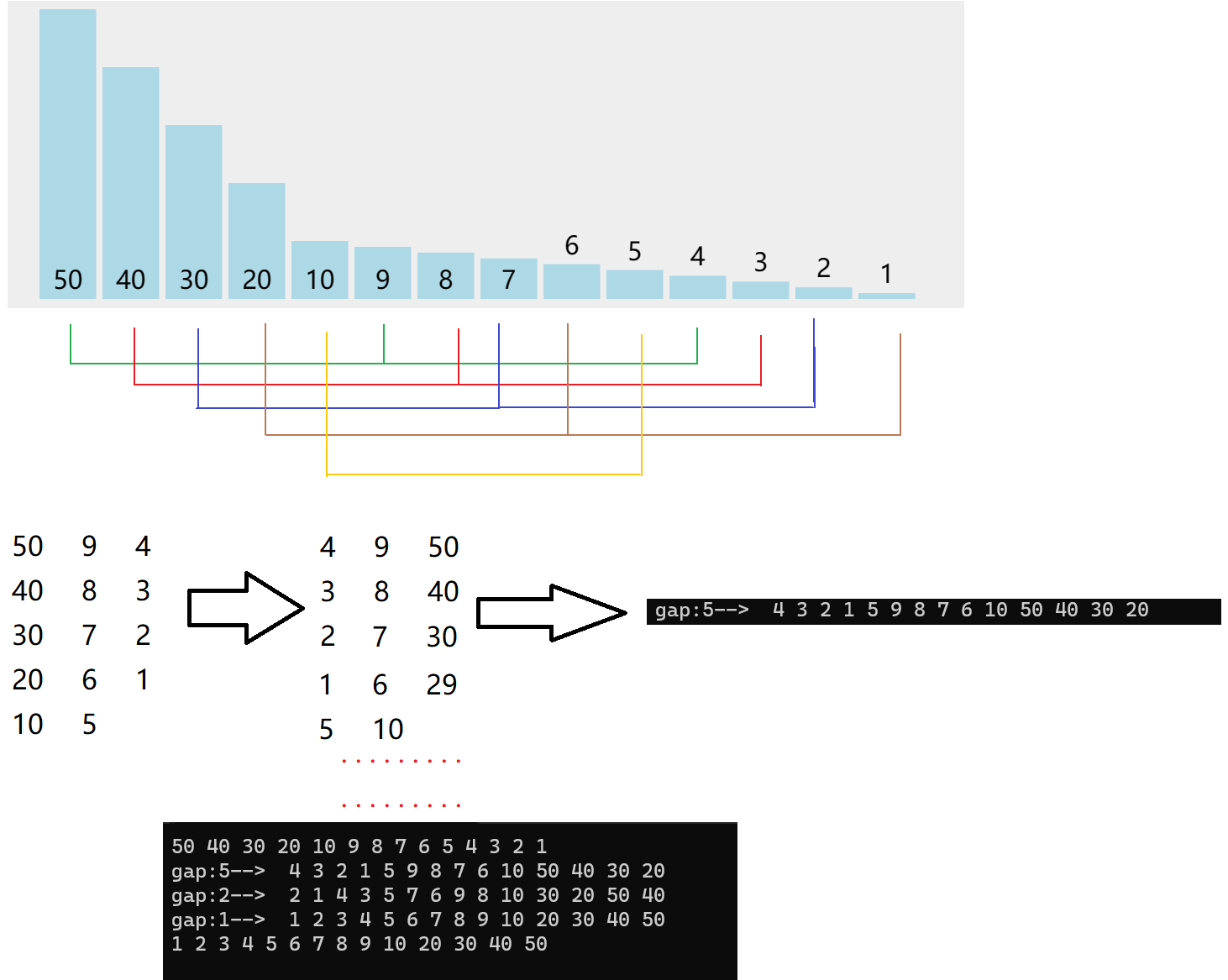
✨1.2 希尔排序
希尔排序是基于直接插入排序的一种优化,将数据分为gap组,对每组进行排序,然后再缩小间隔,知道gap为1的时候,该序列为有序
//希尔排序
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){//最后一次gap一定要是1gap = gap / 3 + 1;//分组插入排序 预排序for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[i + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}elsebreak;}a[end + gap] = tmp;}}
}
希尔排序特性:
希尔排序有2层循环,一个是
gap的逐渐缩小,一个是分为gap组之后的插入排序,我们一般以为时间复杂度为**O(N*logN)**这个量级。但其实这其中的N,一直是在变化的,可理解为先上升,后下降
所以这个量级是略大于N*logN,查阅资料可得知,希尔排序的时间复杂度大概为O(N1.3~2)
稳定性:不稳定
🎊2. 选择排序
还是以打扑克来举例,有时候我们感觉一张一张摸牌十分费时间,所以就指定一个人来发牌,发完之后我们将这一把牌拿到手中再开始理牌
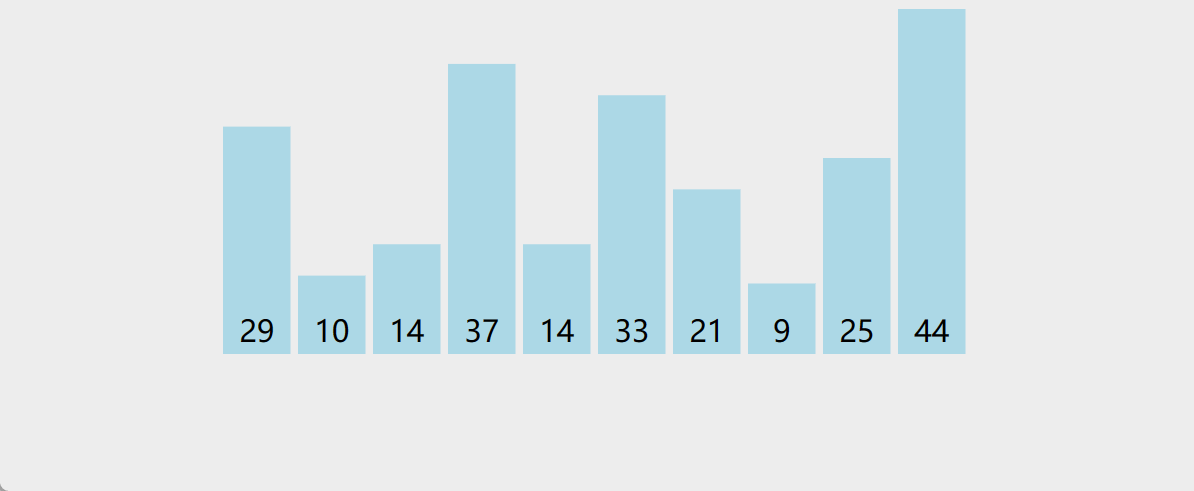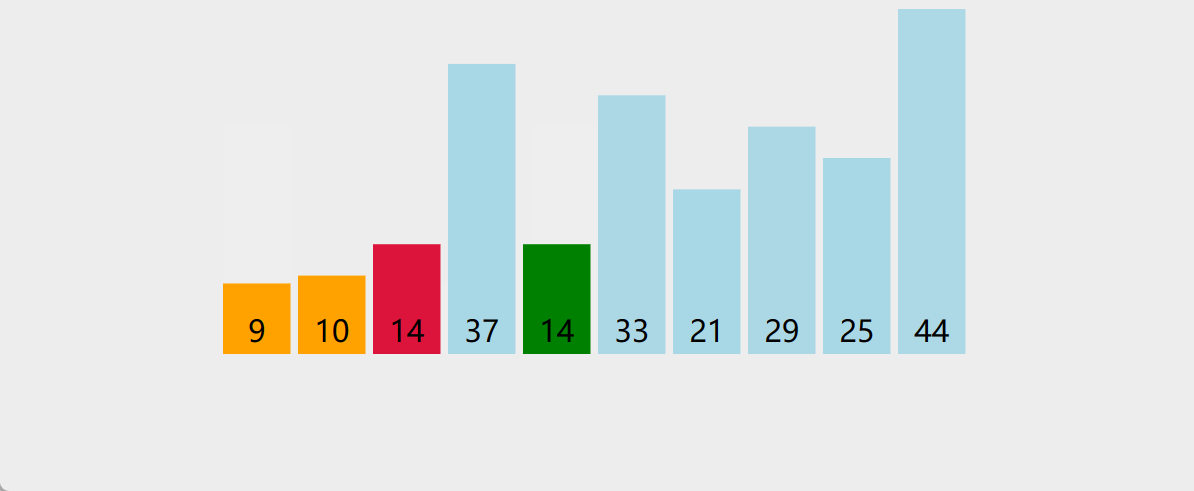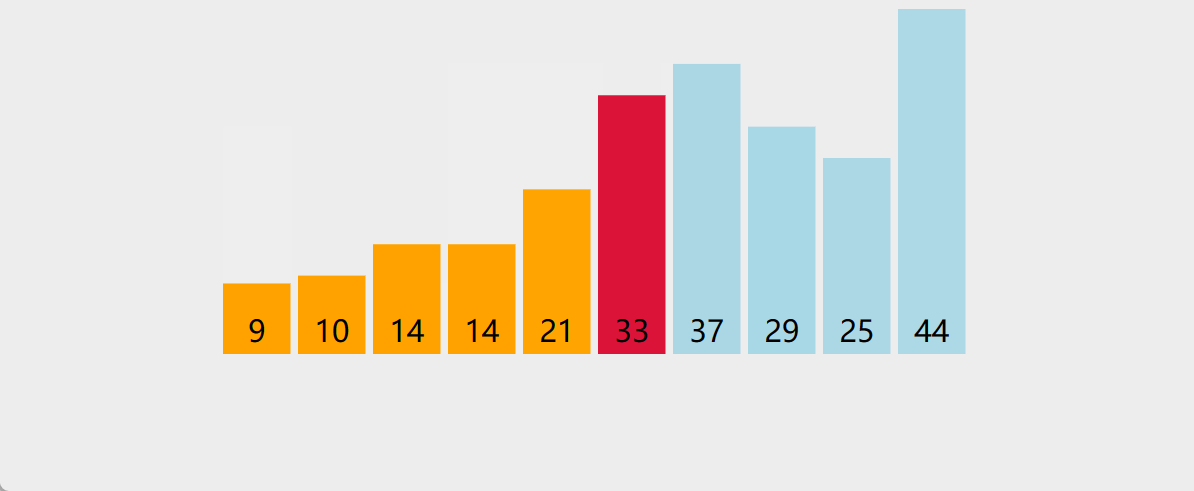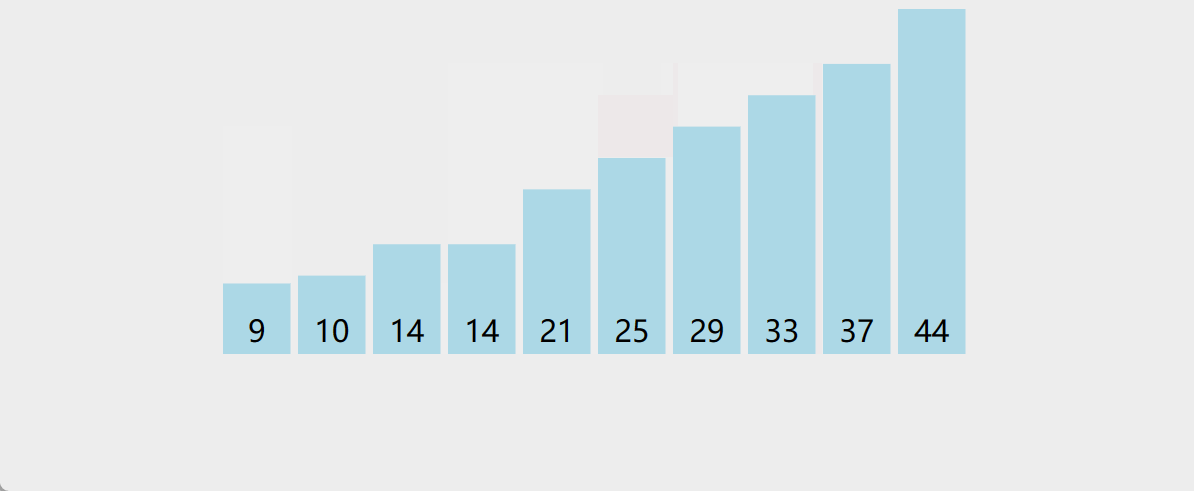
🎋2.1 直接选择排序
这个选择排序每次都是趟都是选出最小的数,我们可以在此基础上做出优化,每次选出2个数,即最小值和最大值
//选择排序
void SelectSort(int* a, int n)
{int left = 0;int right = n - 1;while (left < right){int mini = left;int maxi = left;for (int i = left + 1; i <= right; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[left], &a[mini]);//数据修正if (a[left] == a[maxi]){maxi = mini;}Swap(&a[right], &a[maxi]);left++;right--;}
}
直接选择排序特性:
不考虑序列的有序性,每次都找出最小最大值,效率较低
时间复杂度:O(N2)
最好情况:O(N2)
最坏情况:O(N2)
空间复杂度:O(1)
稳定性:不稳定
🎋2.2 堆排序
堆排序也是选择排序的一种,只不过没有直接选择排序那么朴实,堆排序有一些“华丽”的技巧。
堆排序在之前二叉树的章节讲过了,这里就不再过多赘述,有兴趣的可以查看此篇文章:数据结构——二叉树
//向下调整 前提:子树都是堆
void AdjustDown(int* val, int sz, int parent)
{//默认左孩子大int child = parent * 2 + 1;//至多叶子结点结束while (child < sz){//不越界 选出更大的孩子if (child + 1 < sz && val[child] < val[child + 1]){child++;}if (val[child] > val[parent]){Swap(&val[child], &val[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//堆排序
void HeapSort(int* a, int n)
{//向下调整 O(N)for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a,n, i);}//向下调整排序 O(N*logN)for (int i = 0; i < n; i++){Swap(&a[0], &a[n - 1 - i]);AdjustDown(a, n - 1 - i, 0);}
}
堆排序特性:
- 堆排序进行选数据效率较高
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
🎏3. 交换排序
🎐3.1 冒泡排序
冒泡排序应该是多数人的启蒙排序算法,思路较为简单
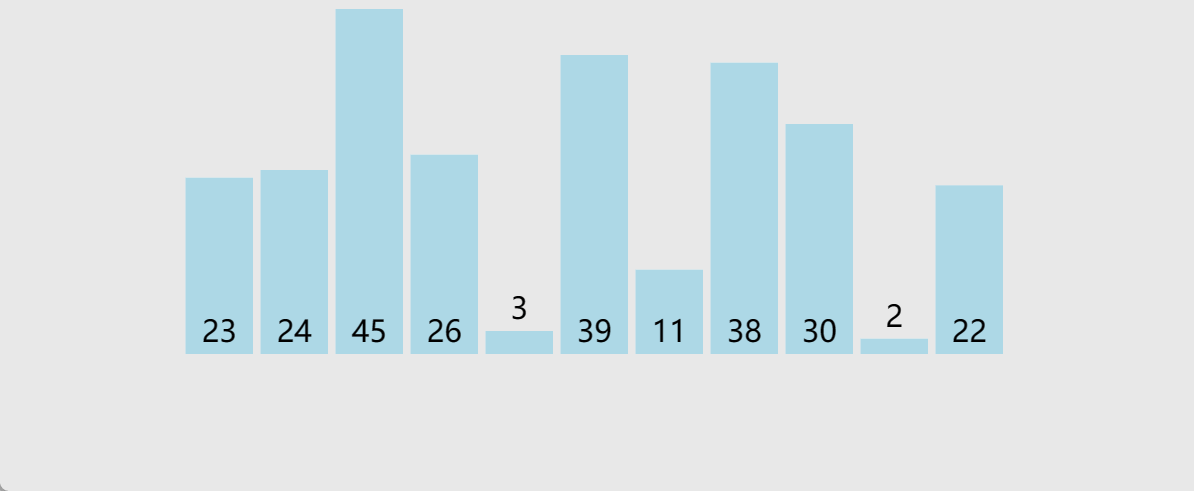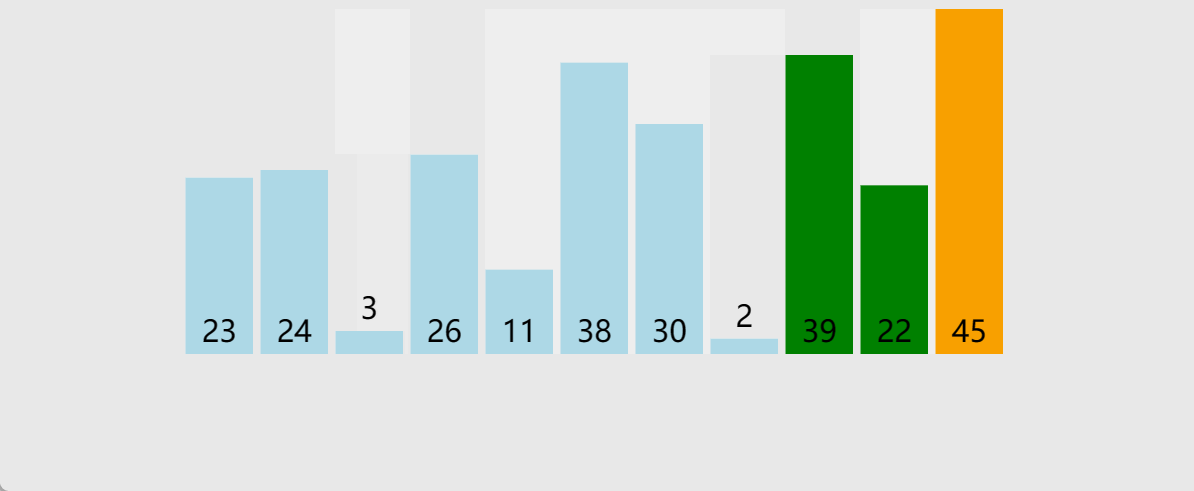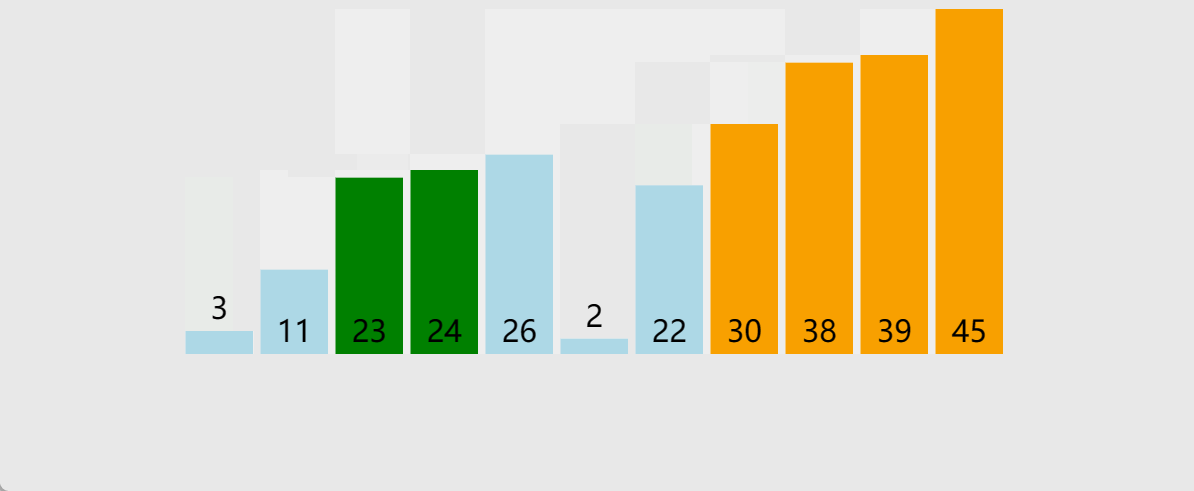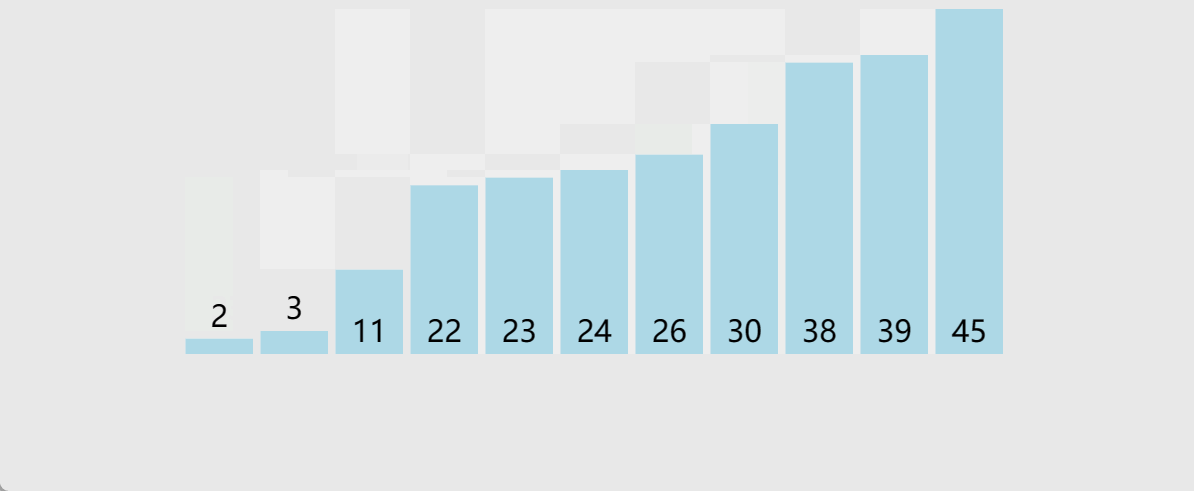
//冒泡排序
void BubbleSort(int* a, int n)
{for (int i = 0; i < n; i++){for (int j = 0; j < n - i - 1; j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);}}}
}
冒泡排序特性:
时间复杂度:O(N2)
最坏情况:O(N2)
最好情况:O(N)
空间复杂度:O(1)
稳定性:稳定
这里的最好情况,就是里面没有发送交换了,就证明此时序列已经有序,则不需要往后再遍历,优化如下:
//冒泡排序
void BubbleSort(int* a, int n)
{for (int i = 0; i < n; i++){bool falg = true;for (int j = 0; j < n - i - 1; j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);falg = false;}}if (falg)break;}
}
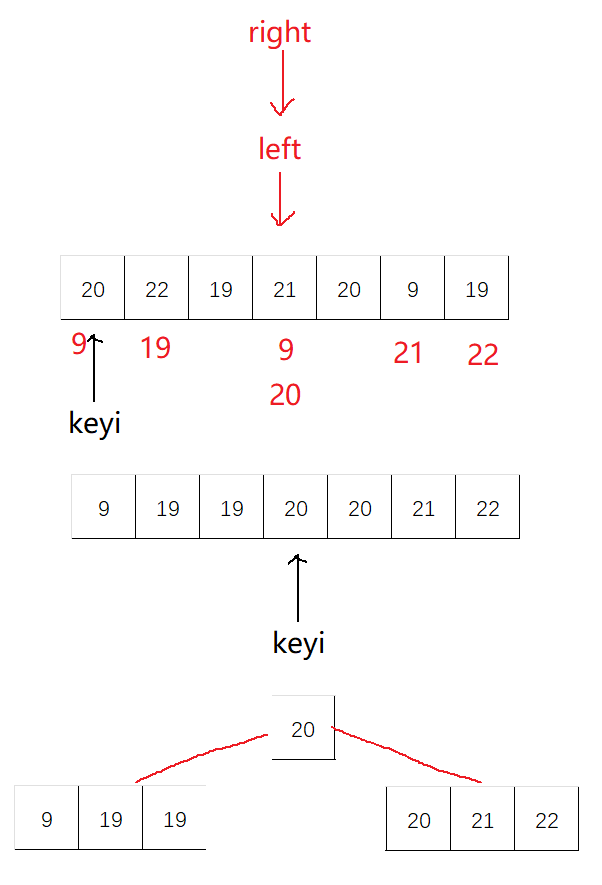
🎐3.2 快速排序
快速排序,顾名思义,速度很快,效率很高,排序算法里面的大哥大
快排的思想是选出一个基准值key,然后把这个值放入正确的位置(最终排好序要去的位置)
例如
6,2,9,1,5,7,4这组数据我们选出6为
key值,然后将比6小的放左边,比6大的放右边这一趟下来,6就在正确的位置上了
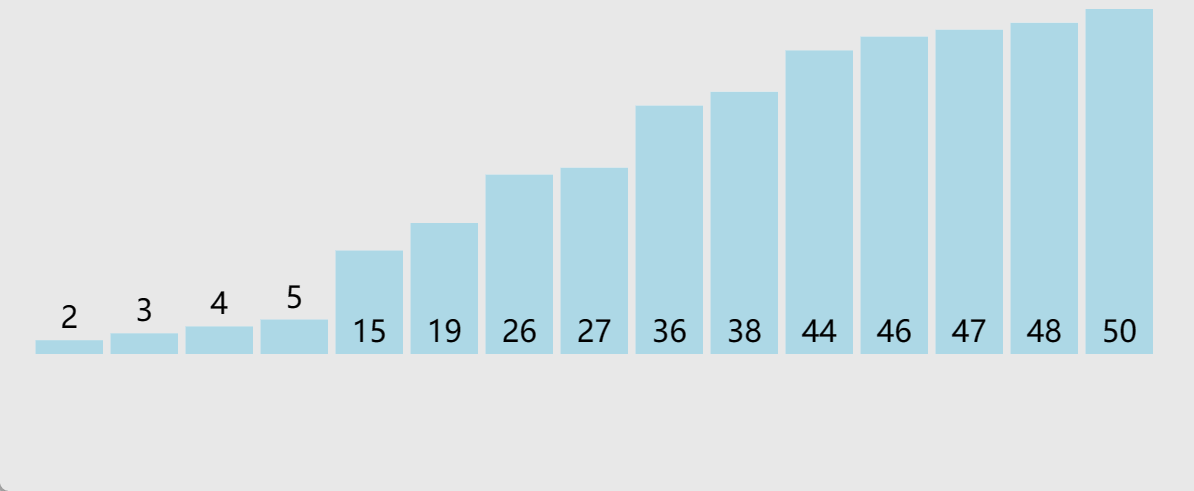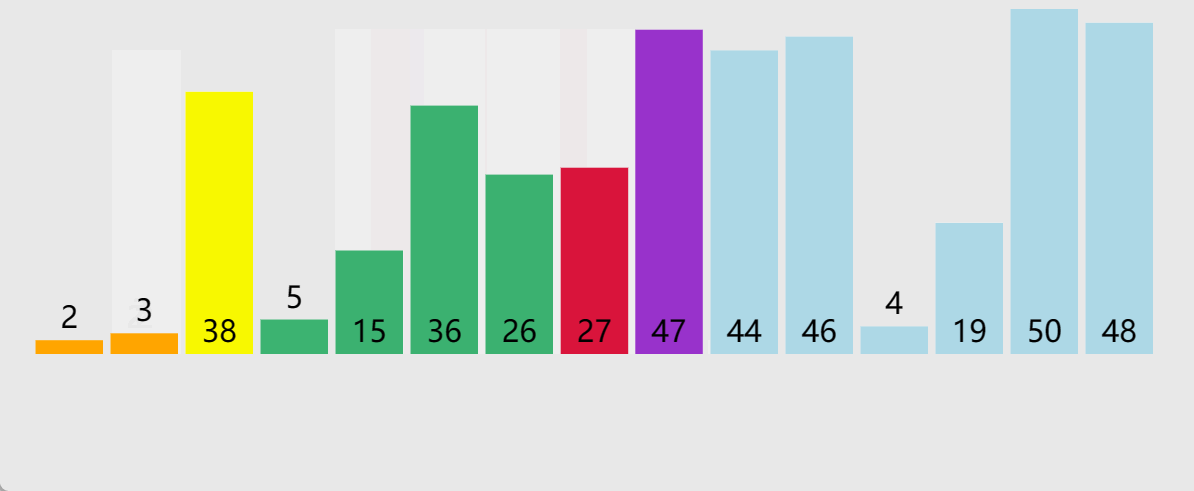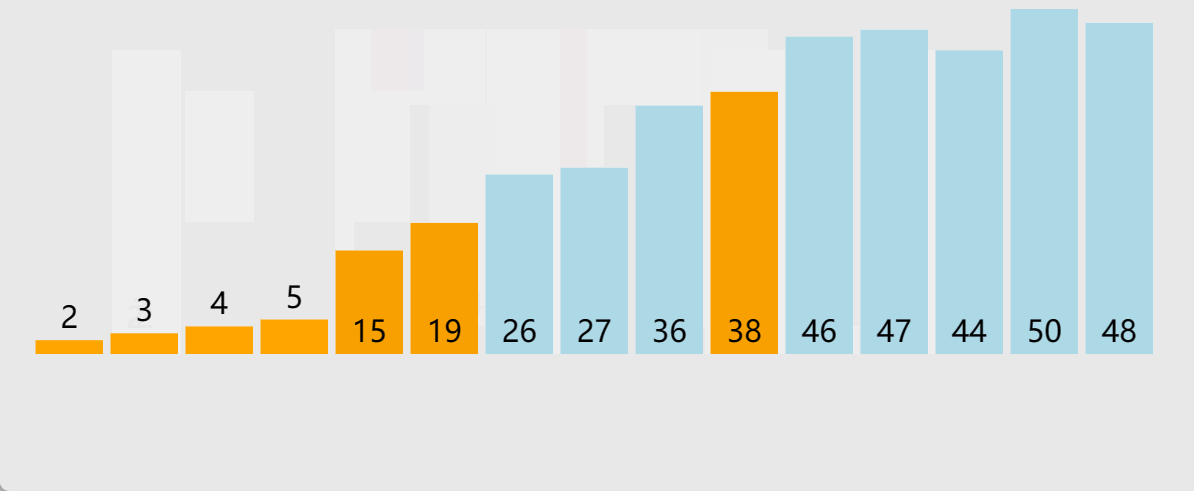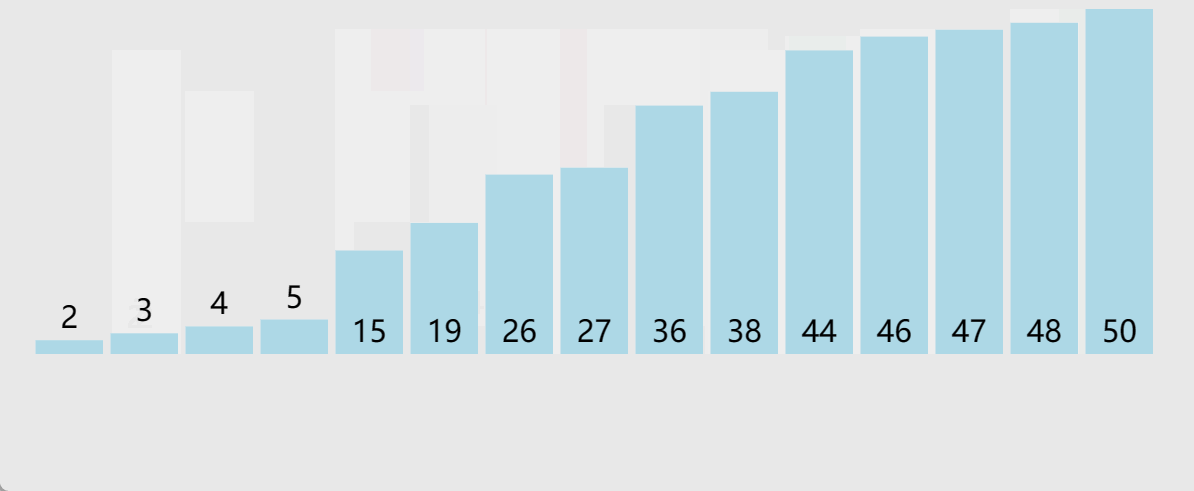
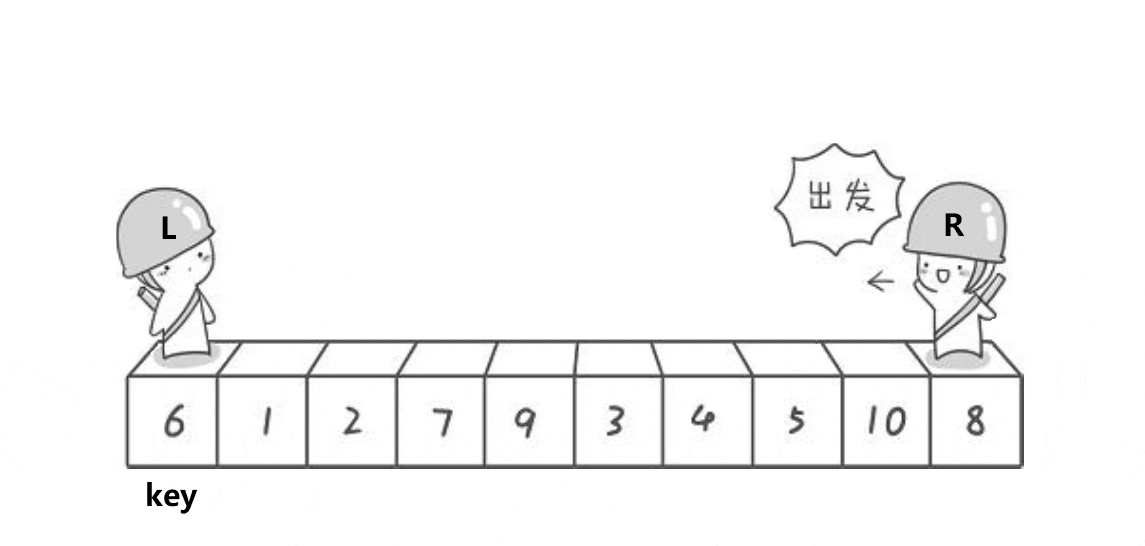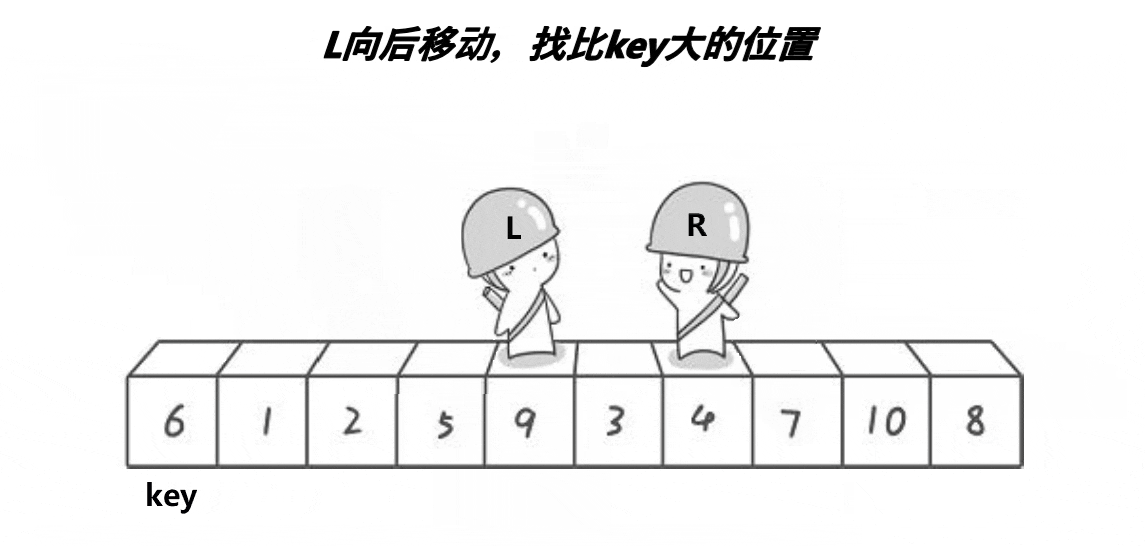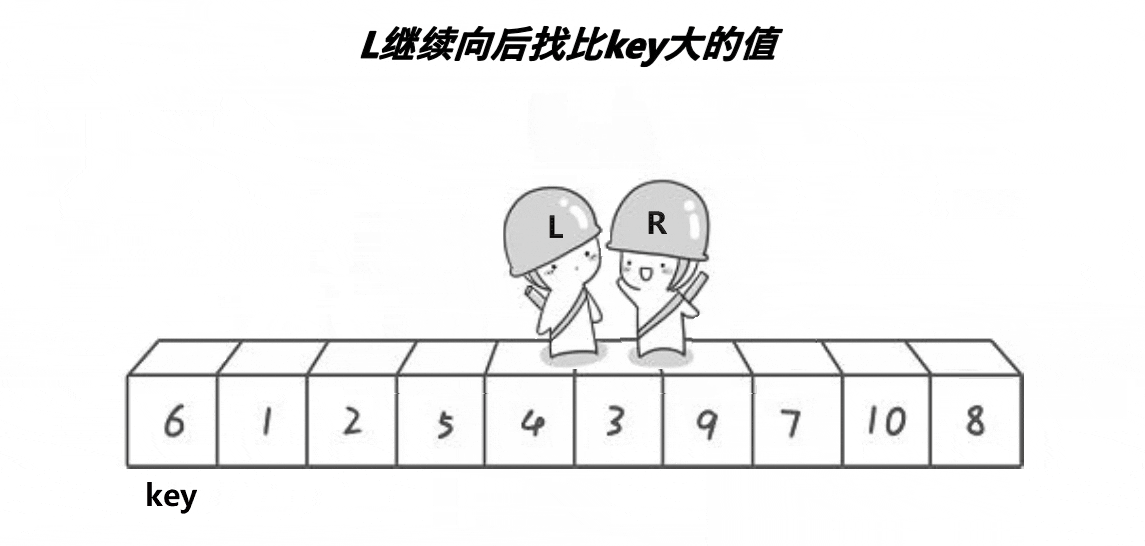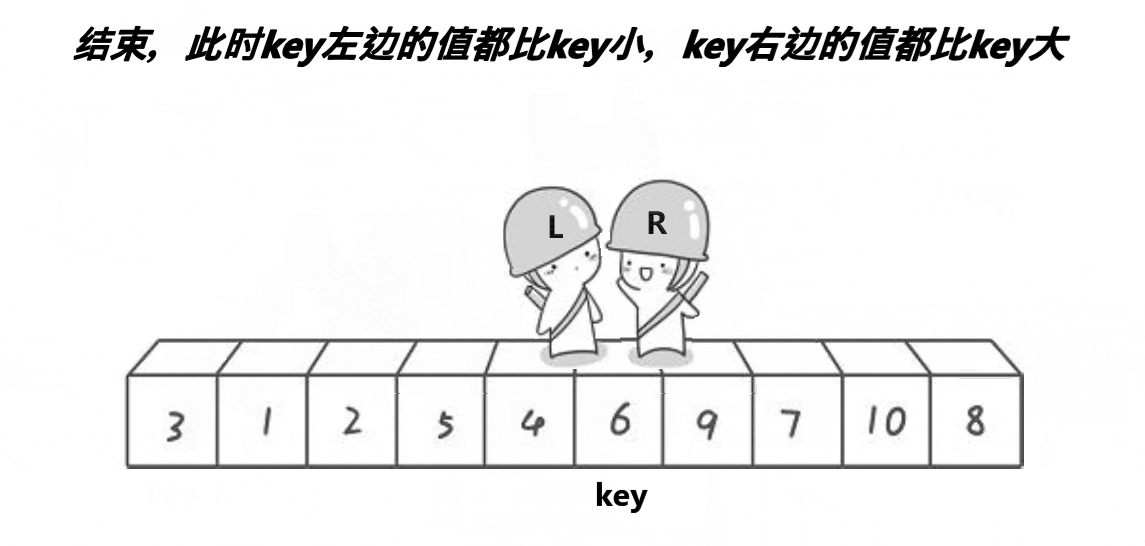
🎑hoare版本
//快速排序
void QuickSort(int* a, int left,int right)
{if (left >= right)return;//记录起始int begin = left;int end = right;//选取最左边为key值int keyi = left;while (left < right){//选左 右先走 找小值while (left<right && a[right] >= a[keyi]){right--;}while (left < right && a[left] <= a[keyi]){left++;}//交换两边的值Swap(&a[left], &a[right]);}Swap(& a[keyi], & a[left]);keyi = left;//左右区间递归QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}
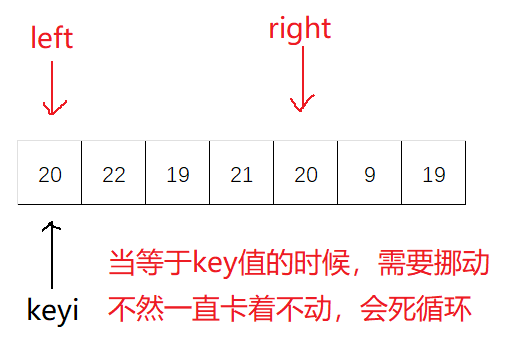
hoare版本为快排的最初始版本,这个版本不容易控制:
找大值/小值的时候,如果该值等于key值,也需要挪动,即
a[right] >= a[keyi]、a[left] <= a[keyi]
另外,判断条件还应加上
left<right,防止越界
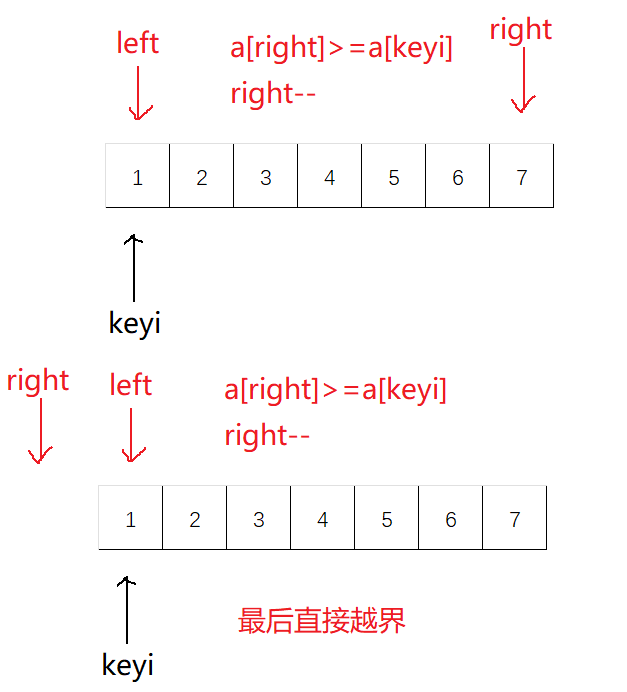
左边作为
key,右边先走,这样就能保证相对位置比key要小或者就是key的位置右边作为
key,左边先走,相遇位置比key大或者就是key的位置已排序或者逆序的情况都是最糟糕的情况
有多少个数据,就有递归多少层栈帧,最终会导致栈溢出
-
随机选
key这个
keyi影响了快排的效率,只要keyi取的数,每次越接近于中间,那么每次就越接近于二分,所以我们可以考虑随机选key,这样就不必担心序列是否接近有序//快速排序 void QuickSort(int* a, int left,int right) {if (left >= right)return;//记录起始int begin = left;int end = right;//left可能不是0,加上leftint randi = left + (rand() % (right - left));//还是选择左边为key,交换一下Swap(&a[left], &a[randi]);//选取最左边为key值int keyi = left;while (left < right){//选左 右先走 找小值while (left<right && a[right] >= a[keyi]){right--;}//左边找大值while (left < right && a[left] <= a[keyi]){left++;}//交换两边的值Swap(&a[left], &a[right]);}Swap(& a[keyi], & a[left]);keyi = left;//[begin,keyi-1] keyi [keyi+1,end]//左右区间递归QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end); } -
三数取中
int GetMidNumi(int* a, int left, int right) {int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right])return mid;else if (a[left] > a[right])return left;elsereturn right;}else //a[left] >a[mid]{if (a[mid] > a[right])return mid;else if (a[left] < a[right])return left;elsereturn right;} } int Partition1(int* a, int left, int right) {//三数取中 开始 中间 末尾 选中间值int midi = GetMidNumi(a, left, right);if (midi != left)Swap(&a[left], &a[midi]);//选取最左边为key值int keyi = left;while (left < right){//选左 右先走 找小值while (left < right && a[right] >= a[keyi]){right--;}//左边找大值while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);keyi = left;return keyi; } void QuickSort(int* a, int left, int right) {if (left > right)return;int keyi = Partition1(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right); }
🎑挖坑法
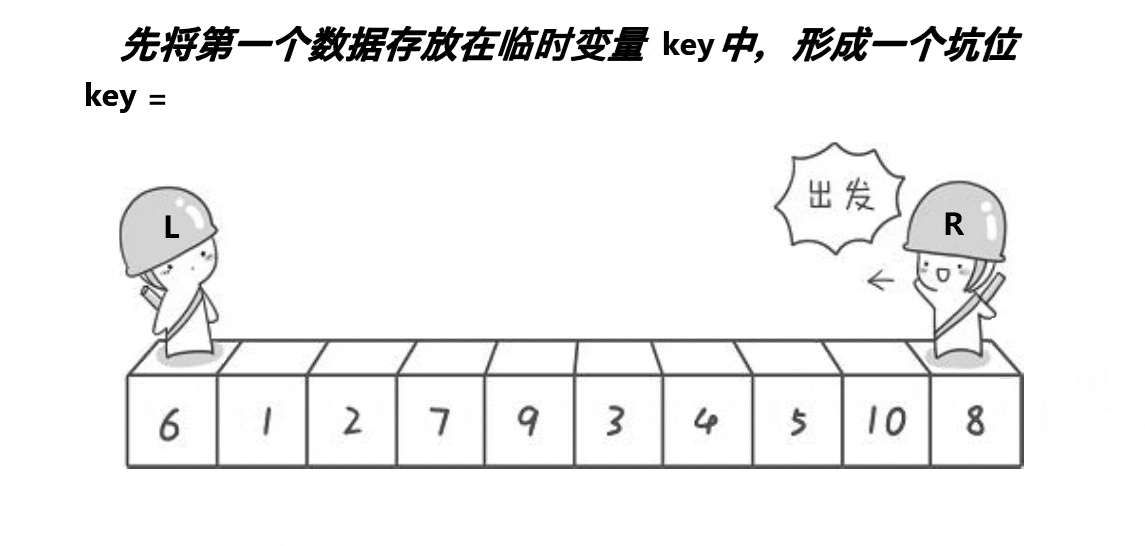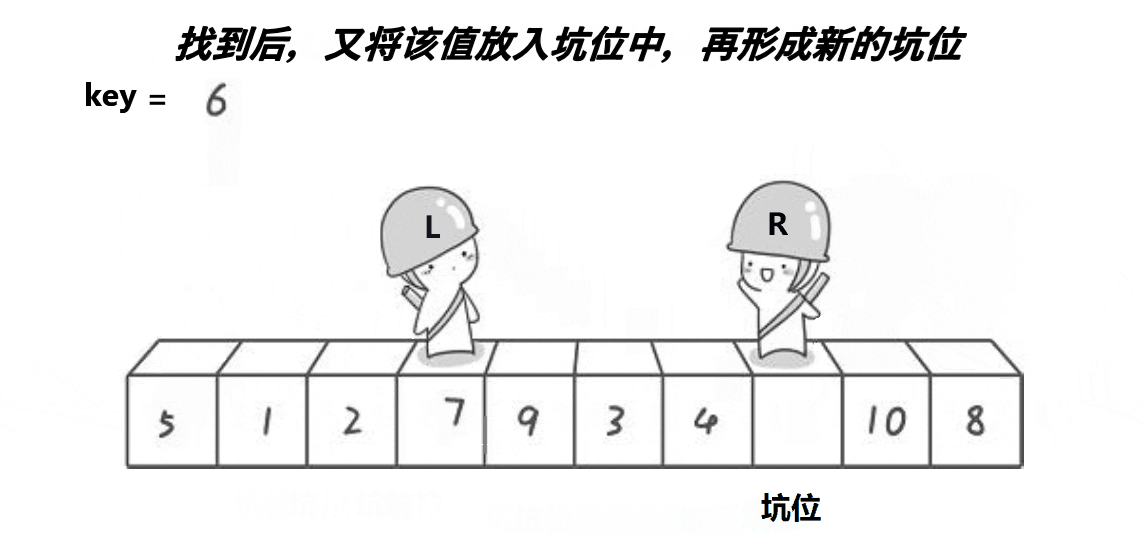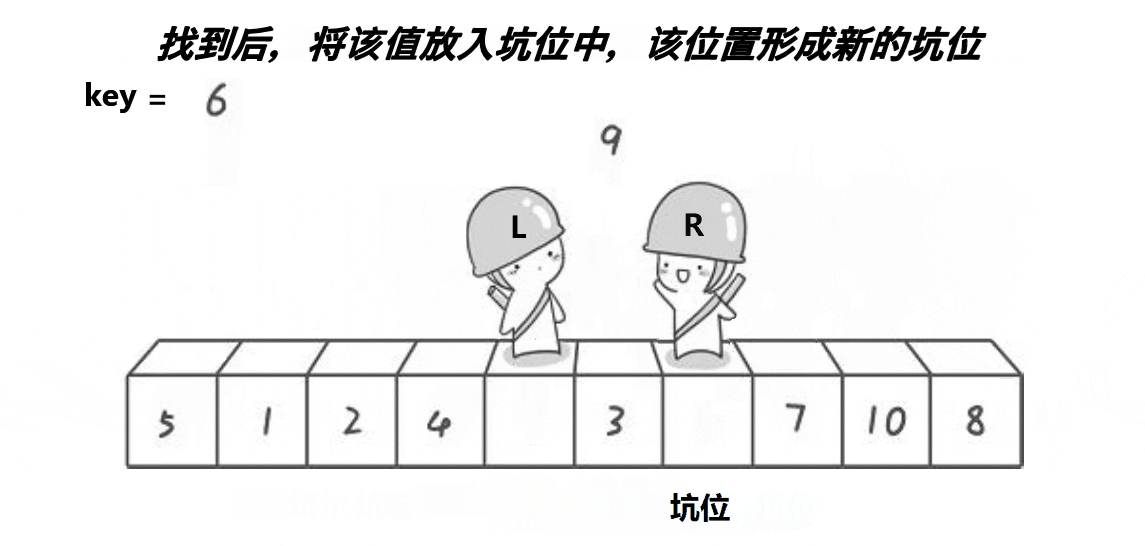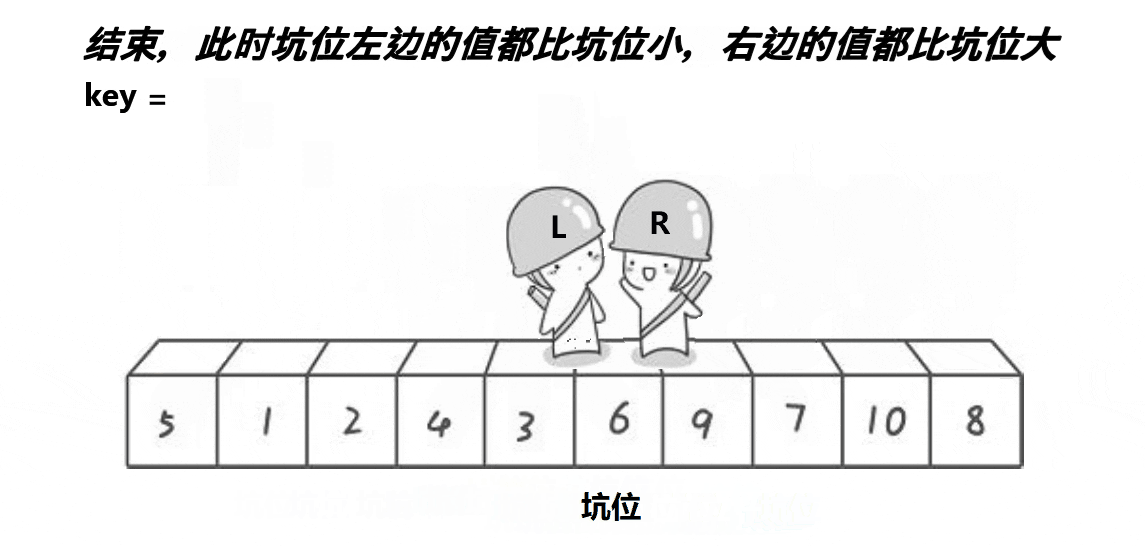
基本思路不边,只是这个更好理解,挖坑填坑、挖坑填坑,最后相遇位置一定是坑位
//挖坑
int Partition2(int* a, int left, int right)
{//三数取中 开始 中间 末尾 选中间值int midi = GetMidNumi(a, left, right);if (midi != left)Swap(&a[left], &a[midi]);//选取最左边为key值int key = a[left];int hole = left;while (left < right){//选左 右先走 找小值while (left < right && a[right] >= key){right--;}//填坑a[hole] = a[right];//挖坑hole = right;//左边找大值while (left < right && a[left] <= key){left++;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}
void QuickSort(int* a, int left, int right)
{if (left > right)return;int keyi = Partition2(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}
🎑前后指针
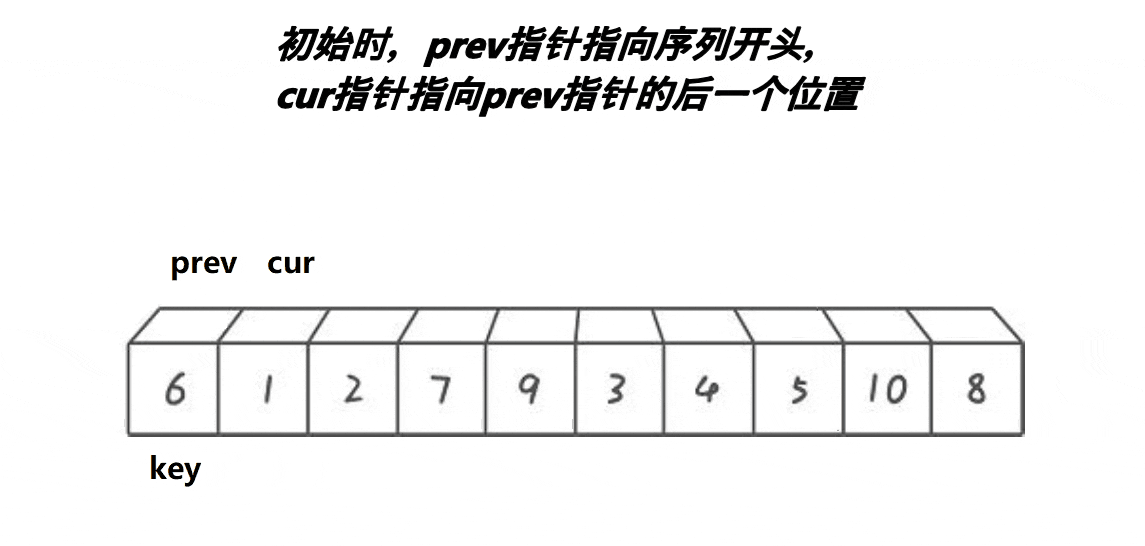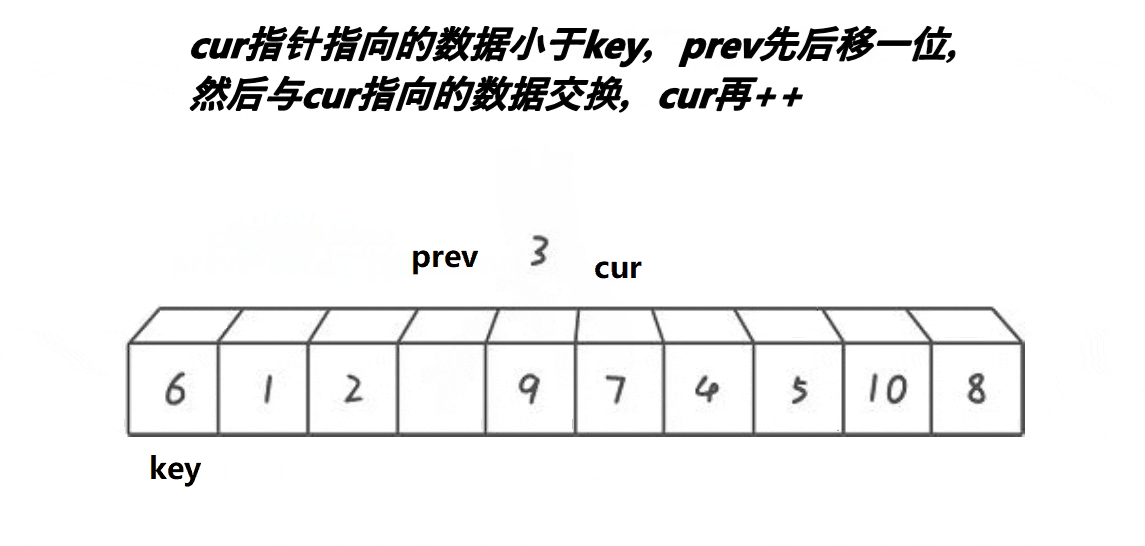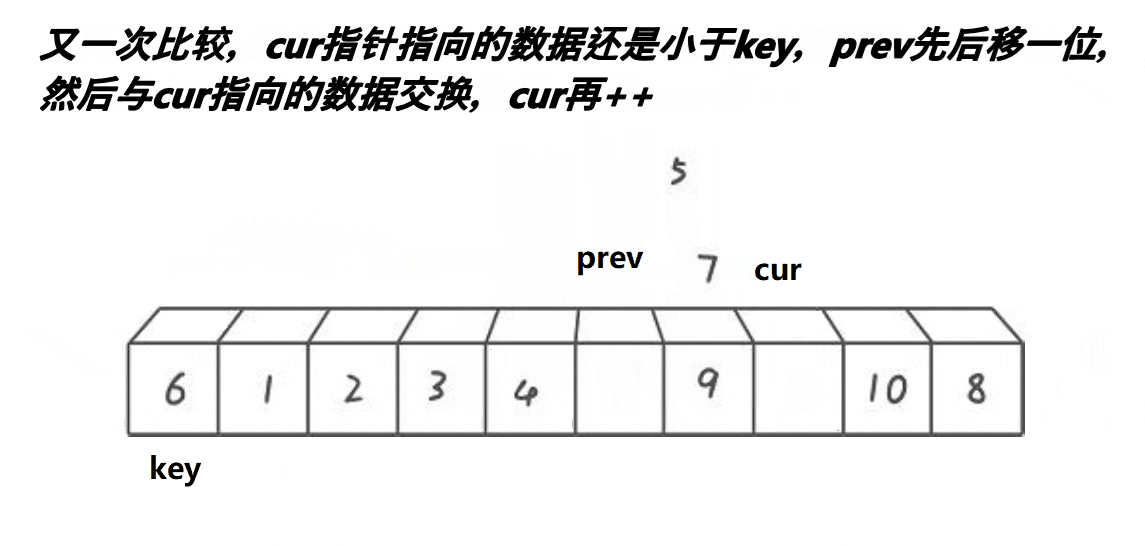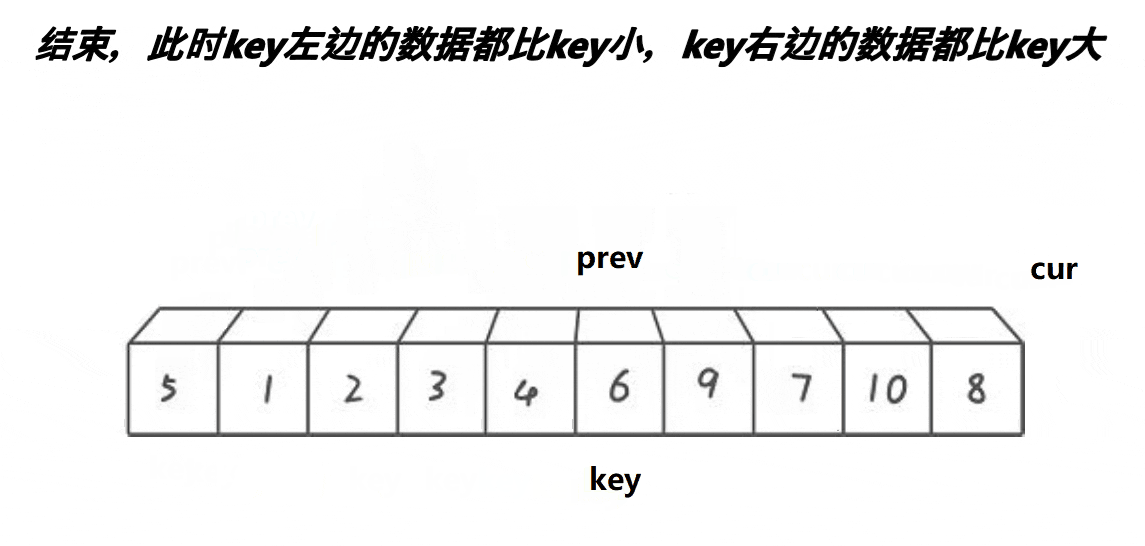
- cur找的值比
key小,++prev,cur与prev位置的值交换,++cur - cur找的值比
key大,++cur
//前后指针
int Partition3(int* a, int left, int right)
{//三数取中 开始 中间 末尾 选中间值int midi = GetMidNumi(a, left, right);if (midi != left)Swap(&a[left], &a[midi]);int keyi = left;int prev = left;int cur = left + 1;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[keyi], &a[prev]);keyi = prev;return keyi;
}
void QuickSort(int* a, int left, int right)
{if (left > right)return;int keyi = Partition3(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}
🎑小区间优化
当大量的数据递归到小量数据的时候,递归就会很麻烦,所以当数据量较小的时候,我们可以采用插入排序进行辅助,直接将这一小段数据排成有序
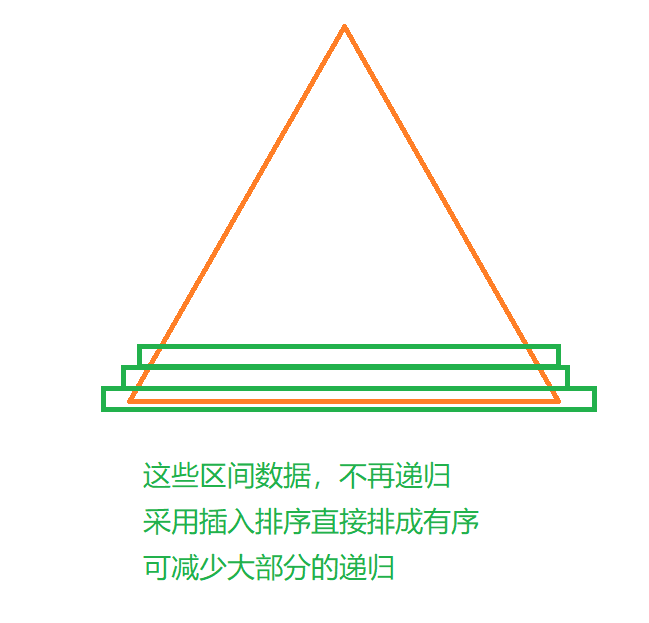
#define INSERTION_SORT_THRESHOLD 10
void QuickSort(int* a, int left, int right)
{if (left > right)return;//区间自己决定 一般采用10左右if ((right - left + 1) > INSERTION_SORT_THRESHOLD){int keyi = Partition2(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}elseInsertSort(a + left, right - left + 1);
}
🎑非递归
模拟递归,将区间放入栈
void QuickSortNonR(int* a, int left, int right)
{//用C++的stl库stack<int> st;st.push(right);st.push(left);while (!st.empty()){int begin = st.top();st.pop();int end = st.top();st.pop();int keyi = Partition2(a, begin, end);//[begin,keyi-1] keyi [keyi+1,end]if (keyi + 1 < end){st.push(end);st.push(keyi + 1);}if (begin < keyi - 1){st.push(keyi - 1);st.push(begin);}}
}
快排特性:
时间复杂度:O(N*logN)
快排比较像二叉树
单趟排序的时间复杂度为O(N),而递归的深度是O(logN),合计起来就是O(N*logN)这个量级
空间复杂度:O(logN)
稳定性:不稳定
🎀4. 归并排序
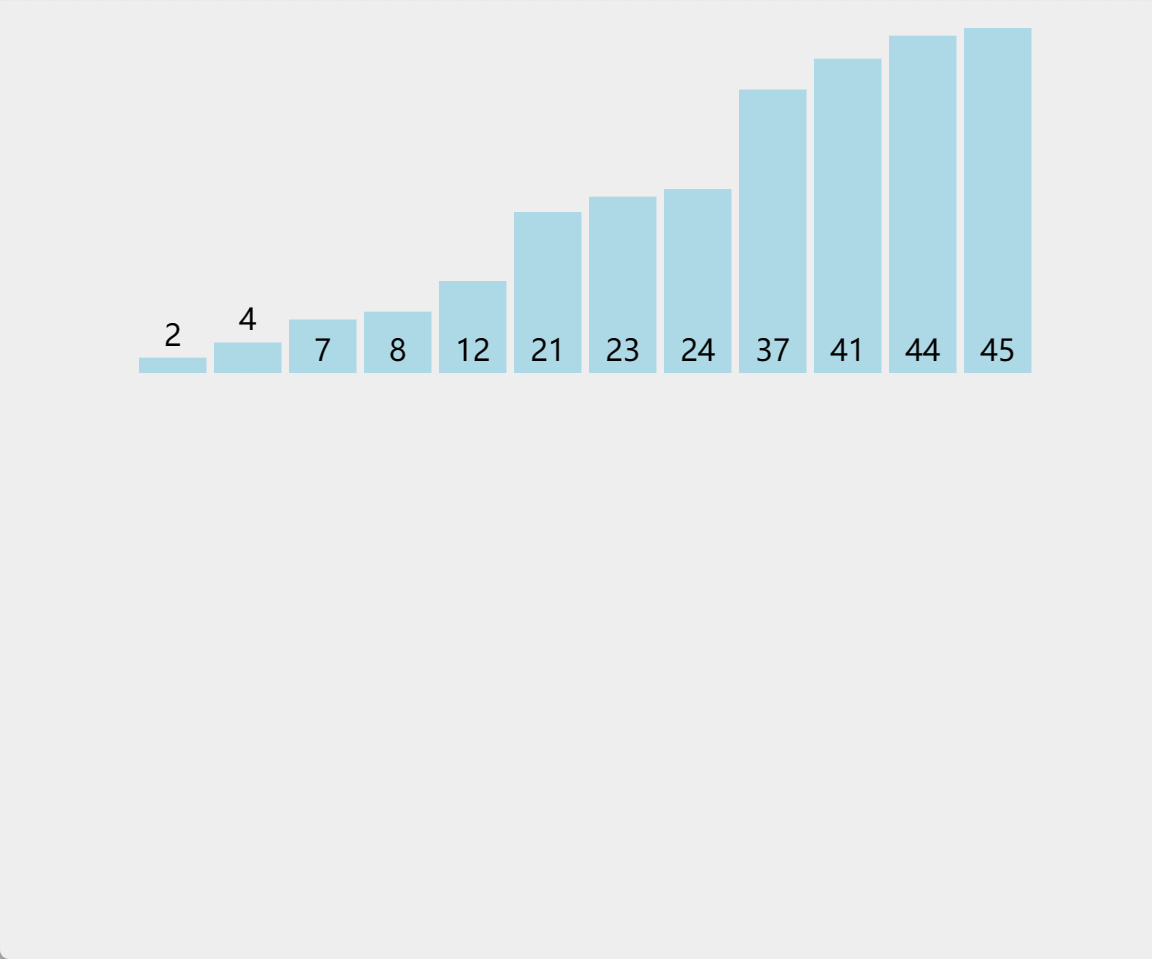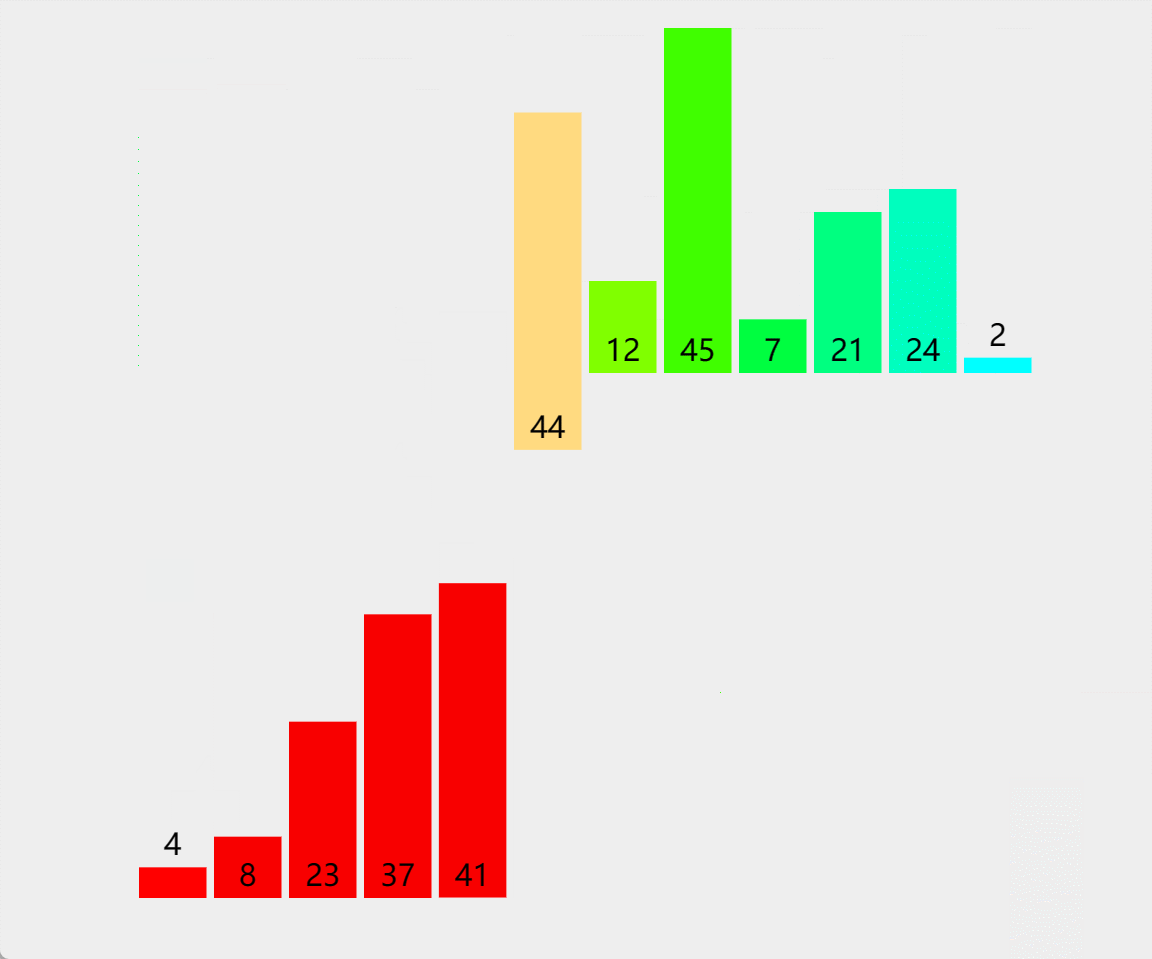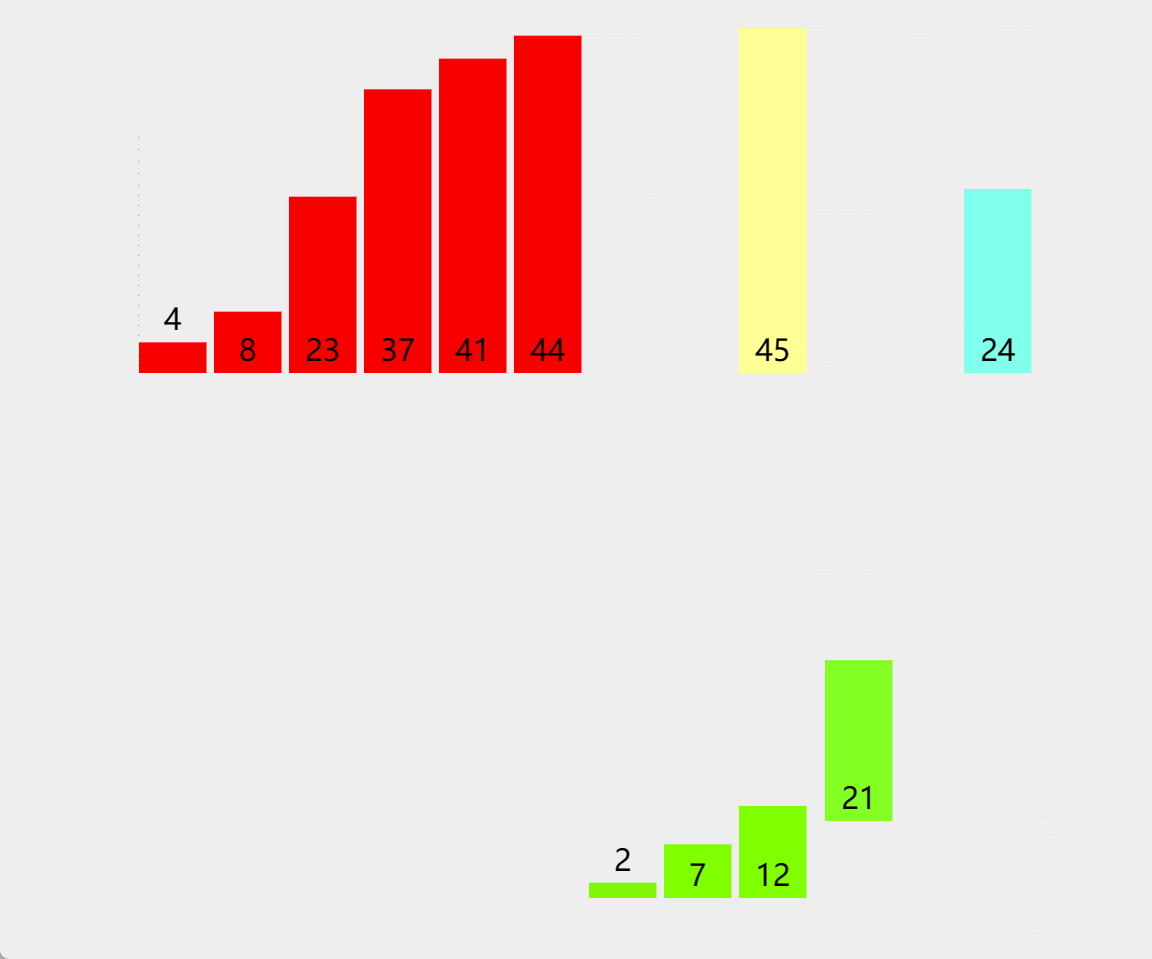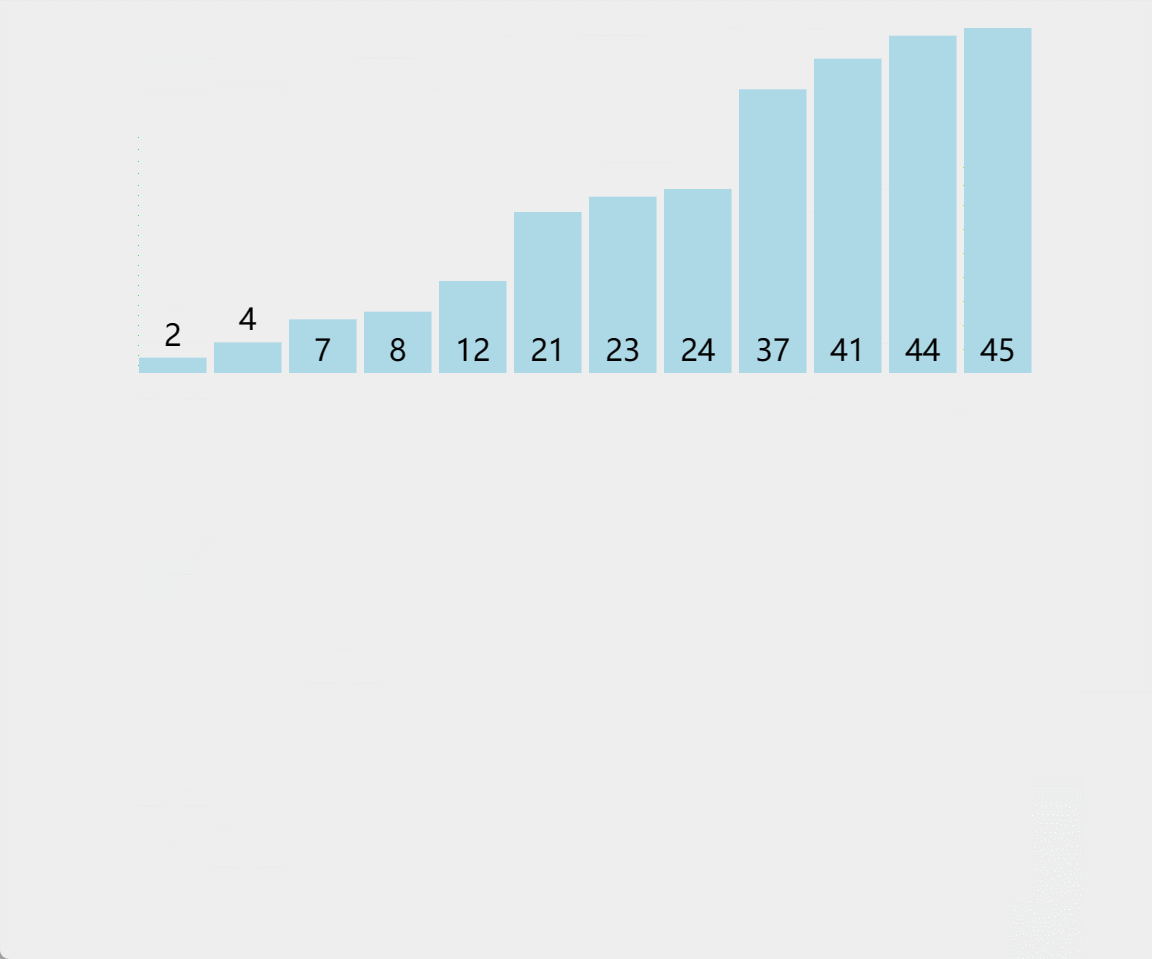
归并排序的思想就是分治,将一个序列看作n个子序列,然后将子序列排好序之后两两归并,这个方法也成为二路归并
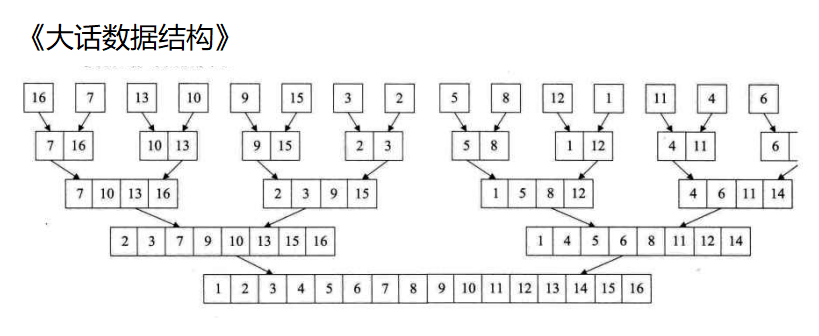
🎁4.1 递归
//归并排序
void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin >= end)return;//分割区间int mid = (begin + end) / 2;//子区间递归排序//[begin,mid] [mid+1,end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid+1, end, tmp);//归并int begin1 = begin;int begin2 = mid+1;int end1 = mid;int end2 = end;int index = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])tmp[index++] = a[begin1++];elsetmp[index++] = a[begin2++];}//防止未结束的区间while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}//拷贝回原序列memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + (int)1));
}void MergeSort(int* a, int n)
{//开辟临时空间int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail\n");exit(-1);}_MergeSort(a, 0, n - 1, tmp);free(tmp);
}
🎁4.2 非递归

归并排序的非递归需要注意的就是边界问题,我们每次都是分为2组归并,如果是单数的话,会发生越界行为,所以要查看这两组的区间:
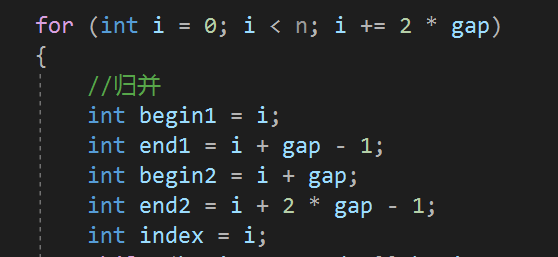
-
begin1,取值为i,所以肯定不会越界 -
end1如果越界,后面的肯定越界,无需进行归并 -
end1没有越界,begin2如果越界,无需进行归并 -
begin2没有越界,end2越界,需要归并,修正end2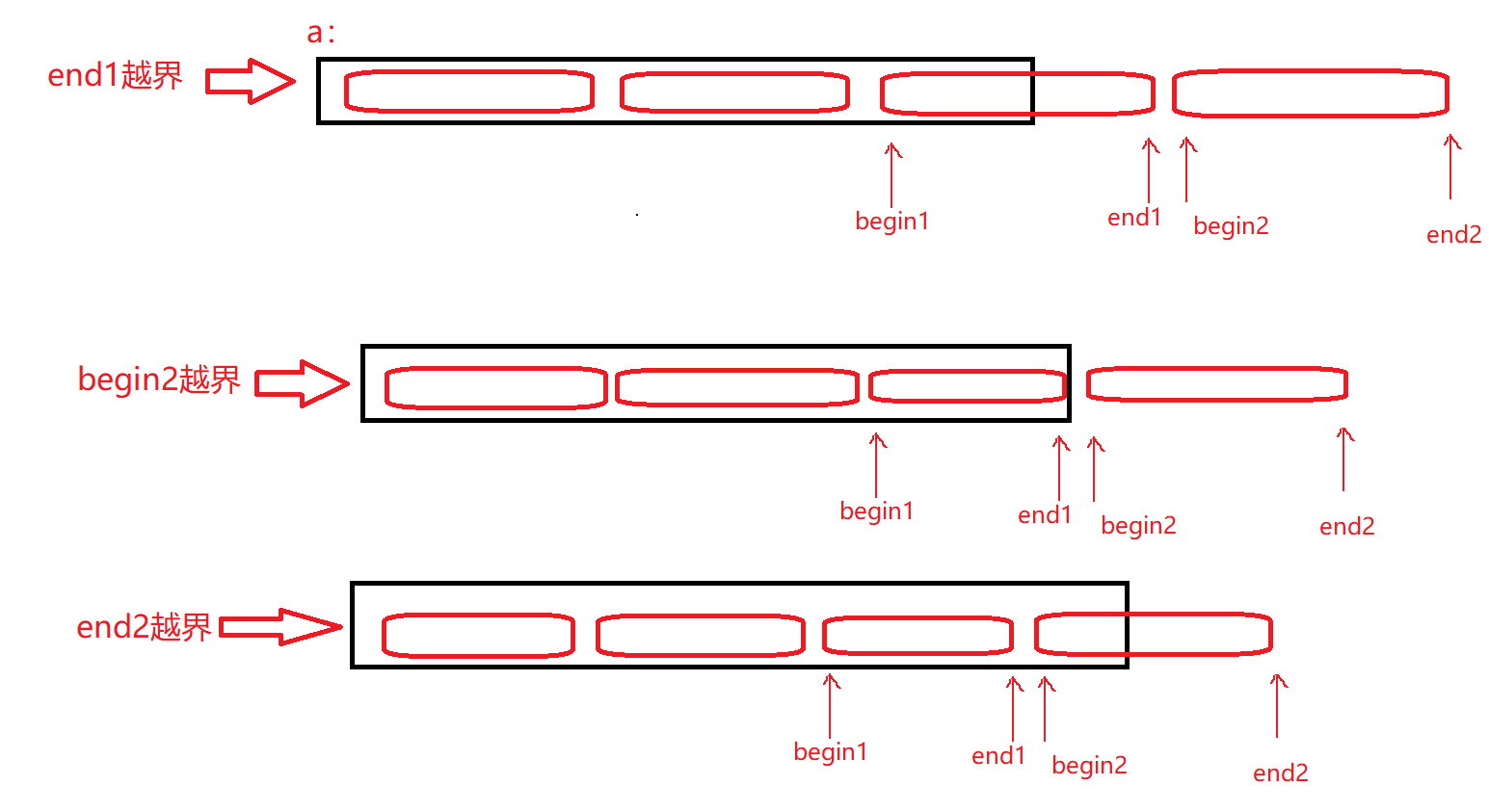
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail\n");exit(-1);}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){//归并int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;//修正 外面一次性拷贝//if (end1 >= n)//{// //不归并// end1 = n - 1;// //给一个不存在区间// begin2 = n;// end2 = n - 1;//}//else if (begin2 >= n)//{// //不归并 修正成不存在的区间// begin2 = n;// end2 = n - 1;//}//else if (end2 >= n)//{// //修正// end2 = n - 1;//}if (end1 >= n || begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}int index = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])tmp[index++] = a[begin1++];elsetmp[index++] = a[begin2++];}//防止未结束的区间while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}//外面拷贝,一把梭哈//memcpy(a, tmp, sizeof(int) * n);gap *= 2;}free(tmp);
}
归并排序特性:
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
- 归并排序更多解决的是磁盘中的外排序问题
🎫5. 性能测试
测试性能我们开
release版本,火力全开;测试环境为Linux的g++
本次只是简单的进行测试,可能会有偶然性
void TestOP()
{srand(time(0));const int N = 10000; //1w//const int N = 100000; //10w//const int N = 5000000; //100w//const int N = 10000000; //1000w//const int N = 100000000; //1亿int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);int* a8 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; i++){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];//a4[i] = 2;a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];a8[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a3, N);int end4 = clock();int begin5 = clock();BubbleSort(a5, N);int end5 = clock();int begin6 = clock();QuickSort(a4, 0, N - 1);int end6 = clock();int begin7 = clock();MergeSort(a6, N);int end7 = clock();std::vector<int> v(a8, a8 + N);int begin8 = clock();std::sort(v.begin(),v.end());int end8 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SeletSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("BubbleSort:%d\n", end5 - begin5);printf("QuickSort:%d\n", end6 - begin6);printf("MergeSort:%d\n", end7 - begin7);printf("STLSort:%d\n", end8 - begin8);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);free(a8);
}
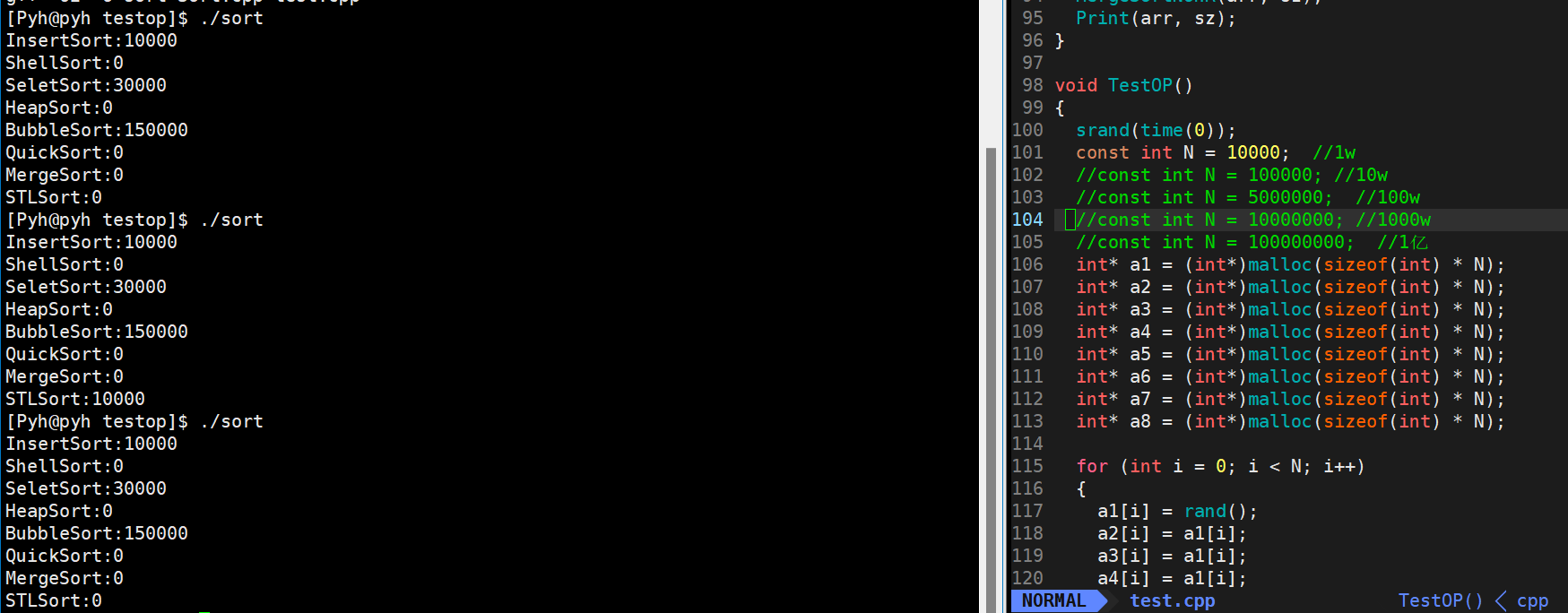
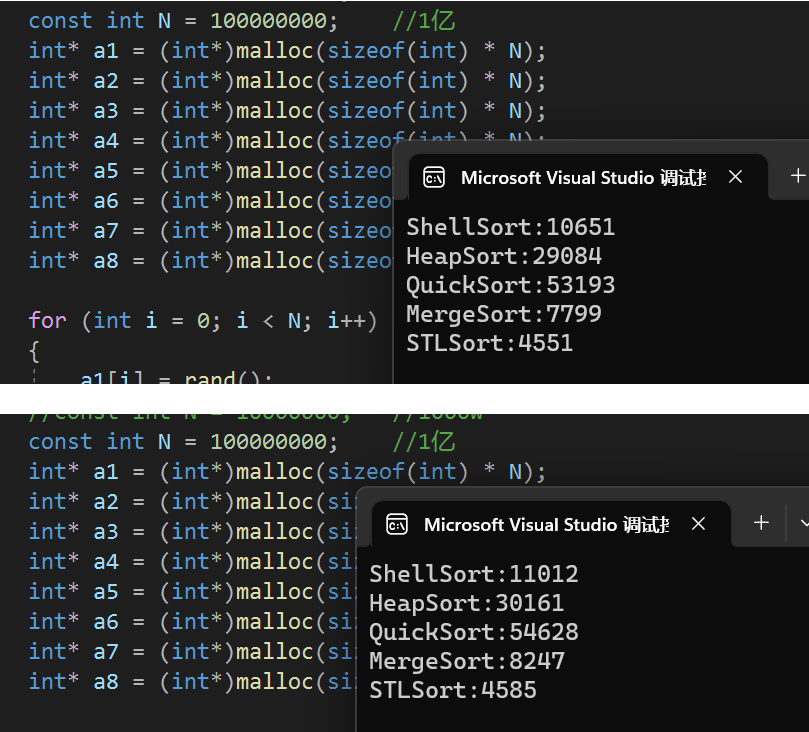
🎖5.1 1w数据
在1w数据这个量级,对于希尔排序、堆排序、快排、归并排序,都是挠痒痒,忽略不计
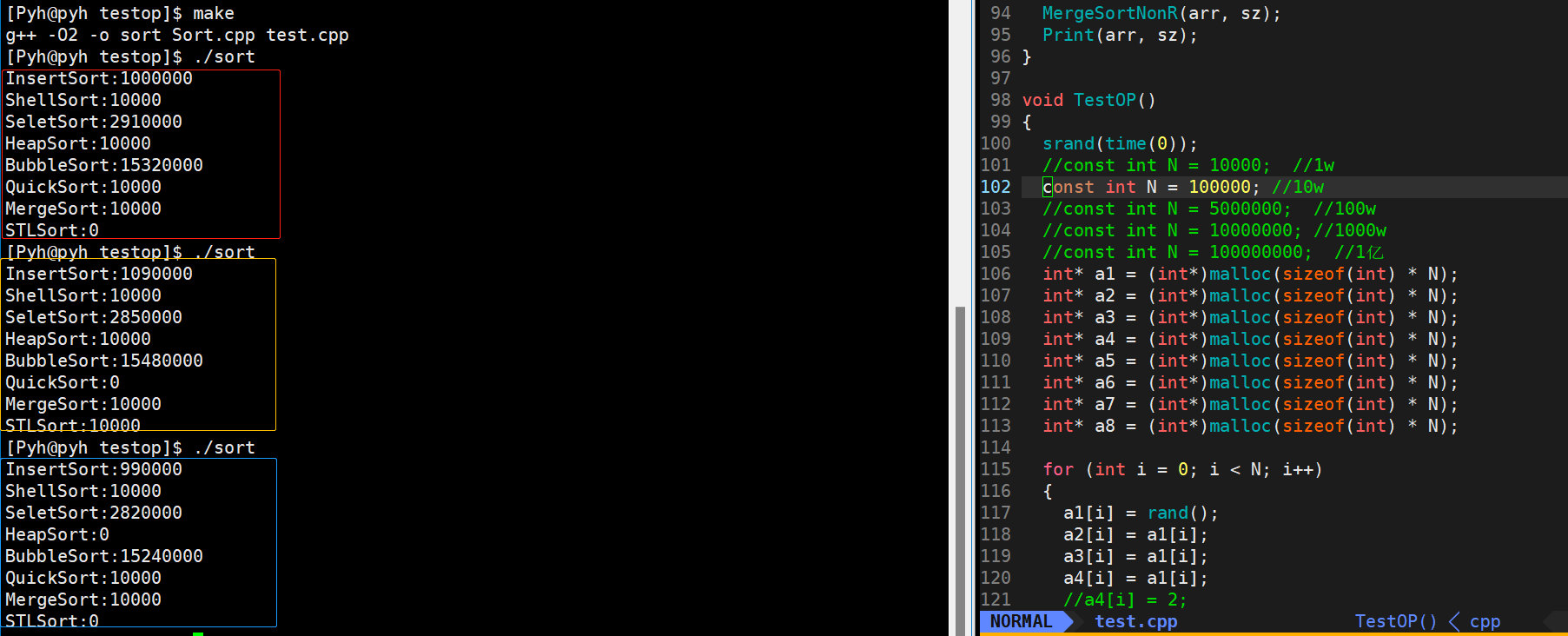
🎖5.2 10w数据
在10w这个量级,显然直接插入排序、直接选择排序、冒泡排序都以不堪重负,而对于这些时间复杂度度在O(N*logN)量级的排序,才刚刚开始
🎖5.3 100w数据
到了100w这个量级,就不再对量级为O(N2)进行测试了,他们坐小孩儿那桌
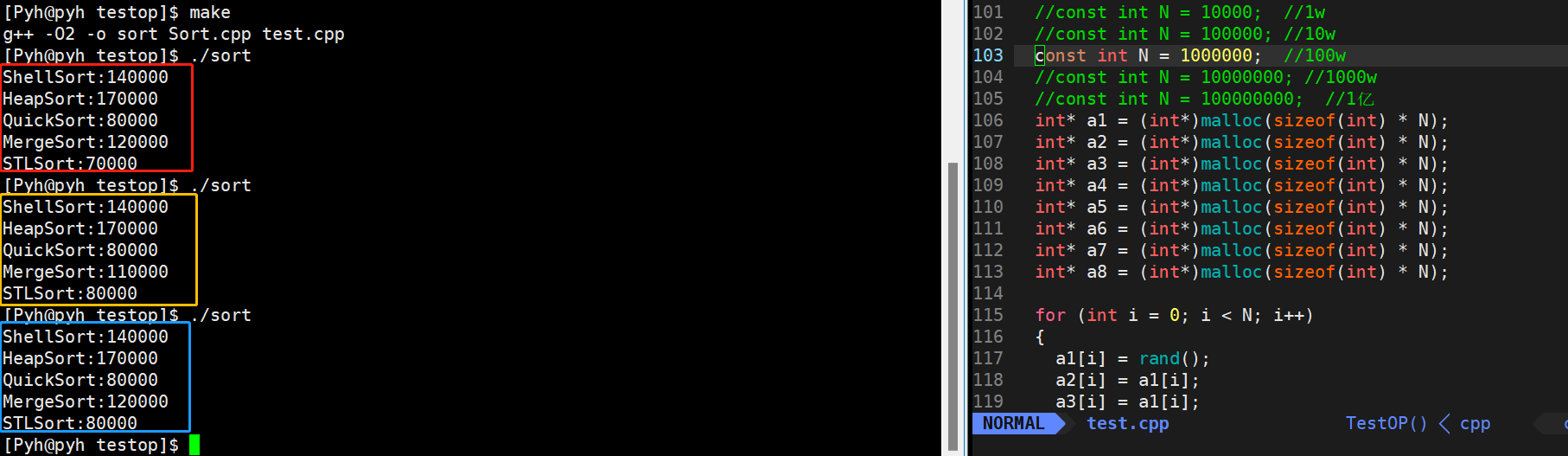
这里可以看出,快排还得是快排
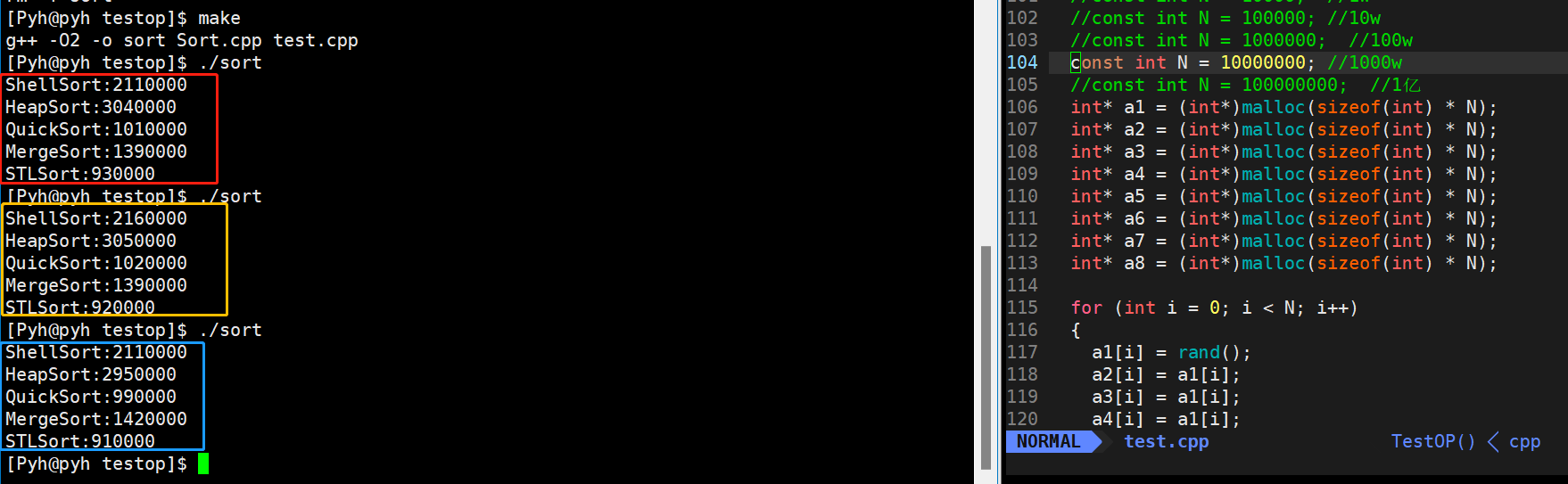
🎖5.4 1000w数据
到1000w这个量级,堆排序就有点扛不住了
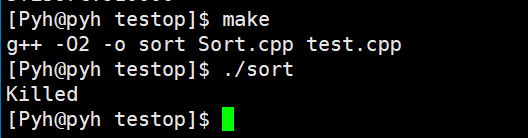
🎖5.5 1亿数据
在一亿这个量级,服务器有点跑不动了
换到Windows环境参考,这个具体还得看机器和优化,不是特别具有参考意义,但可以看一下C++库里面的快排实现
那本期的分享就到这里,我们下期再见,如果还有下期的话。
相关文章:

数据结构——七大排序[源码+动图+性能测试]
本章代码gitee仓库:排序 文章目录 🎃0. 思维导图🧨1. 插入排序✨1.1 直接插入排序✨1.2 希尔排序 🎊2. 选择排序🎋2.1 直接选择排序🎋2.2 堆排序 🎏3. 交换排序🎐3.1 冒泡排序&#…...
G. The Morning Star
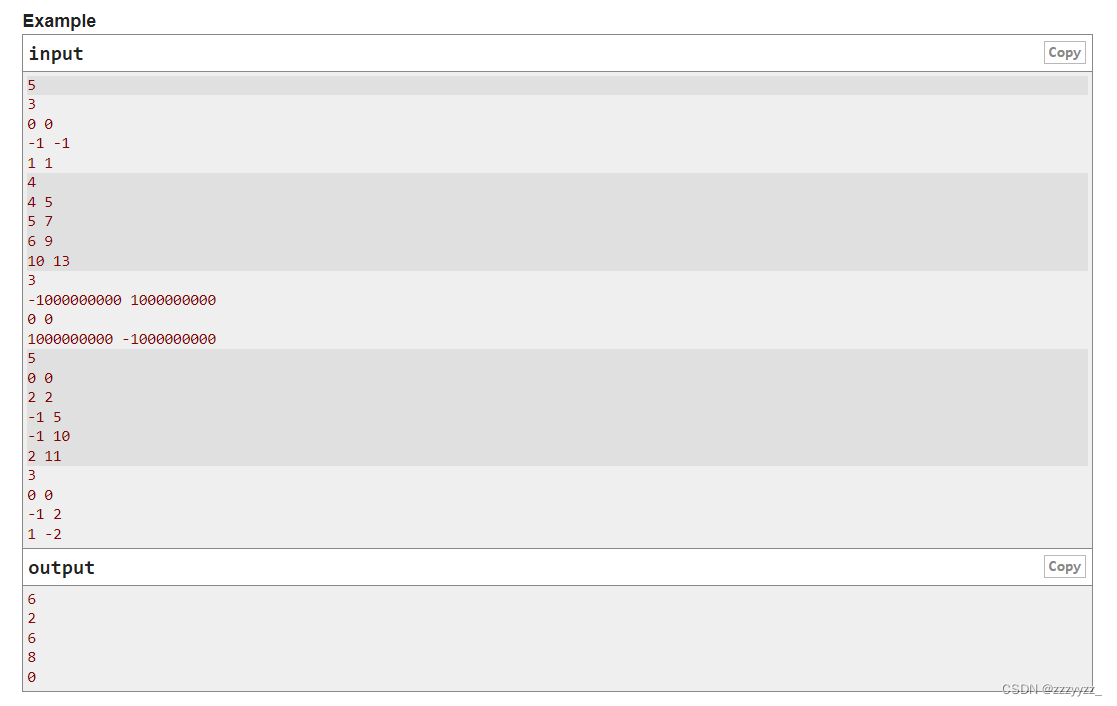
Problem - G - Codeforces 思路:想了挺长时间的,一直没想到一个简便的方法在瞎搞。我们发现对于某个点来说,其他的点如果能够跟他匹配,那么一定在这8个方向上,而同时这8个方向其实对应这4条直线,假设点为(x…...
电池的健康状态 SOH 估计
电池的健康状态 SOH 估计 SOH(State of Health)估计通常用于描述电池的健康状态,即电池当前容量与初始容量的比值。 一种常见的SOH估计方法是基于经验的电池寿命预测方法,包括循环周期数法、安时法与加权安时法、面向事件的老化…...
详解)
Web 安全之 Permissions Policy(权限策略)详解
什么是 Permissions Policy(权限策略)? Permissions Policy 为 web 开发人员提供了明确声明哪些功能可以在网站上使用,哪些功能不能在网站上使用的机制。可以设置一组策略,用于限制站点代码可以访问的 API 或者修改浏…...

【黄啊码】nginx如何设置php运行的
禁止访问 PHP 脚本可以通过 Nginx 服务器配置中的多种方式来实现。以下是其中的一些常见方法,您可以根据实际需求选择合适的方式: 1 禁用 PHP 解析: 在 Nginx 配置中,确保 PHP 脚本无法被解析,从而禁止 PHP 执行。 lo…...

无涯教程-JavaScript - ISPMT函数
描述 ISPMT函数计算在特定投资期间支付的利息。提供此功能是为了与Lotus 1-2-3兼容。 语法 ISPMT (rate, per, nper, pv)争论 Argument描述Required/OptionalRateThe interest rate for the investment.RequiredPerThe period for which you want to find the interest, an…...

LeetCode 面试题 03.05. 栈排序
文章目录 一、题目二、C# 题解 一、题目 栈排序。 编写程序,对栈进行排序使最小元素位于栈顶。最多只能使用一个其他的临时栈存放数据,但不得将元素复制到别的数据结构(如数组)中。该栈支持如下操作:push、pop、peek 和…...
构建微服务项目时启动网关服务失败的解决方案
启动网关服务时报“Unable to create the temporary folder: C:\WINDOWS\TEMP\/nio-file-upload”错误。 代码与之前没有任何变化,但就是启动不了,观察错误意思大概是不能创建临时文件夹:C盘下的WINDOWS下的TEMP目录下的nio-file-upload这个东…...
零基础教程:使用yolov8训练无人机VisDrone数据集
1.准备数据集 1.先给出VisDrone2019数据集的下载地址: 链接:https://pan.baidu.com/s/1e2Q0NgNT-H-Acb2H0Cx8sg 提取码:31dl 2.将数据集VisDrone放在datasets目录下面 2.数据集转换程序 1.在根目录下面新建一个.py文件,取名叫…...

【Mysql专题】使用Mysql做排行榜,线上实例
背景 我们这里有个需求,对存量用户的余额做排行处理,这个实现方式很多,这边介绍的是,通过Mysql直接实现,将排名也直接返回出来。 我知道大家在网上能找到一大把这种实例,我在这里可不是【重复造轮子】。我…...
matlab数据处理: cell table array+datetime
原数据文件.csv matlab xlsread(filename{i},B2:T2881) 会同于Excel最多1048576行 舍弃 a{1,i} xlsread(filename{i},‘B2:T2881’);%读取excel文件,选定区域’B2:G2881’ readcell(filename{i},Range,E2:M2881) 会全部读取 优选 对于日期 yyyy-MM-dd HH:mm:ss.000 matlab cel…...
如何应用运营商大数据精准营销?
如何应用运营商大数据精准营销? 越来越多的企业逐渐觉察到运营商大数据所带来的商业价值,精准营销也被他们用的越来越娴熟。那么,企业的大数据精准营销该如何应用呢?想必是很多资源有限的中小型公司最想了解的。 一 数据驱动运营…...
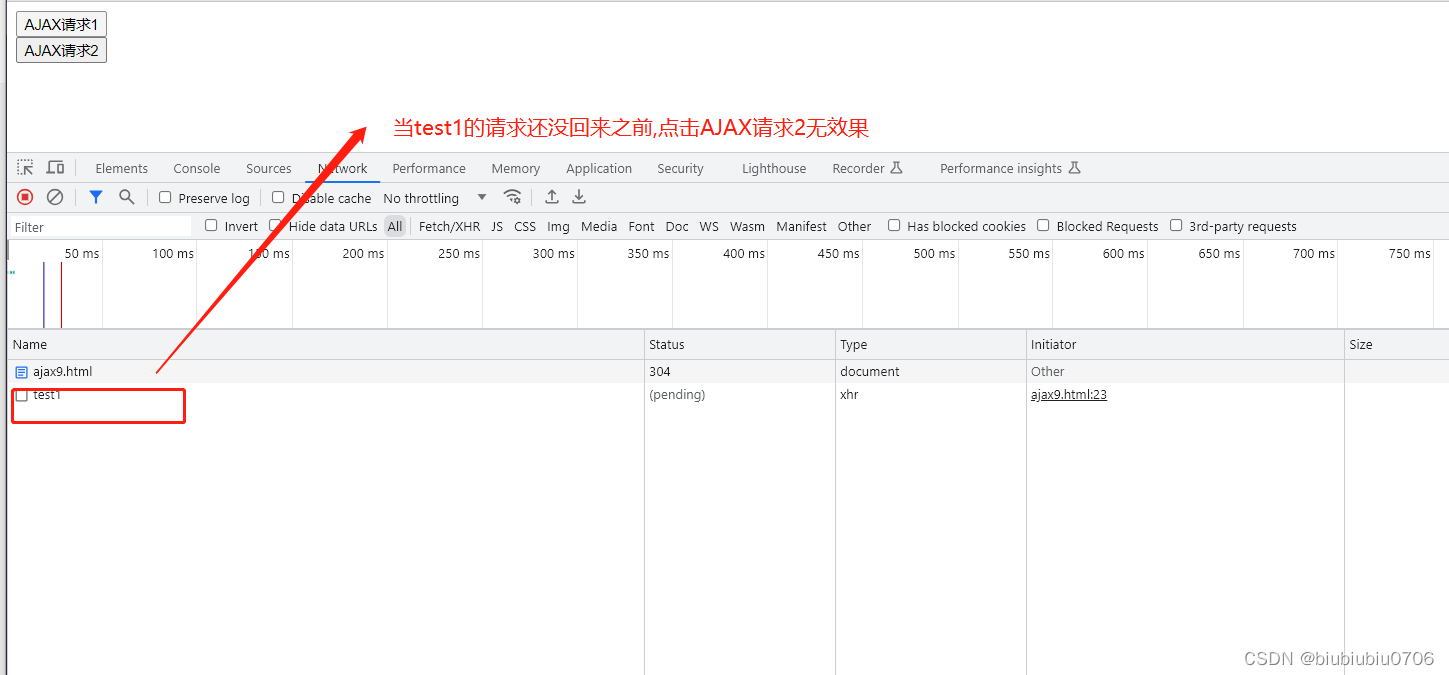
AJAX学习笔记5同步与异步理解
AJAX学习笔记4解决乱码问题_biubiubiu0706的博客-CSDN博客 示例 前端代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>演示AJAX同步和异步</title> </head> <body> <script…...

911面试
WebPack分包 webpack分包 ts泛型 ts泛型 优化if-else和switch 优化if-else 左侧固定,右侧自适应 左侧固定,右侧自适应...
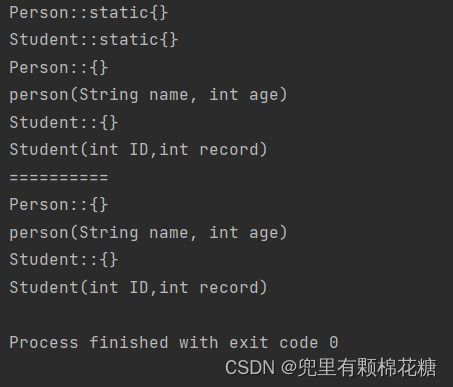
【Java基础篇 | 面向对象】—— 继承
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【JavaSE_primary】 本专栏旨在分享学习JavaSE的一点学习心得,欢迎大家在评论区讨论💌 继承允许一个类继承另一个…...

DELL precision上安装nvidia A4000驱动 cuda cudnn
一、安装驱动 参考这篇文章进行安装Ubuntu安装Nvidia显卡驱动_Kevin__47的博客-CSDN博客 【出现问题】 禁用nouveau后出现黑屏,有几行代码,断线一直在闪 【解决方法】 1、参考这篇文章Ubuntu20.04安装nvidia显卡驱动并解决重启后黑屏问题_ubuntu安装…...

数据结构算法刷题(29)动态规划
思路一:回溯:按照选和不选的判断方式,使用回溯来解决这个问题。 class Solution: def rob(self, nums: List[int]) -> int: n len(nums) #数组的长度 def dfs(i): if i<0: #到达边界条件后 return 0 #返回最大金额是0 res max(dfs(i…...

W11下CMake MinGW配置OpenCV和Qt
💂 个人主页:风间琉璃🤟 版权: 本文由【风间琉璃】原创、在CSDN首发、需要转载请联系博主💬 如果文章对你有帮助、欢迎关注、点赞、收藏(一键三连)和订阅专栏哦 前言 前几天将cuda版本的opencv给编译成功了,当时用的VS的MSVC&…...

反转字符串 反转字符串 || 反转字符串 |||
思想总结:首先将字符串转变为字符数组,再进行遍历并反转字符。 1.反转字符串 代码: class Solution {public void reverseString(char[] s) {reverse(s,0,s.length); //左闭右开}public static void reverse(char[] ch,int i,int j) { 翻转函…...

XML解析 不允许有匹配 _[xX][mM][lL]_ 的处理指令目标
以上错误是在解析xml参数时候报出的。 我这里错误的原因在于,<?xml version\"1.0\" encoding\"UTF-8\"?>少了个空格,参考下图: 下面一行才是对的。...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

用 FFmpeg 实现 RTMP 推流直播
RTMP(Real-Time Messaging Protocol) 是直播行业中常用的传输协议。 一般来说,直播服务商会给你: ✅ 一个 RTMP 推流地址(你推视频上去) ✅ 一个 HLS 或 FLV 拉流地址(观众观看用)…...
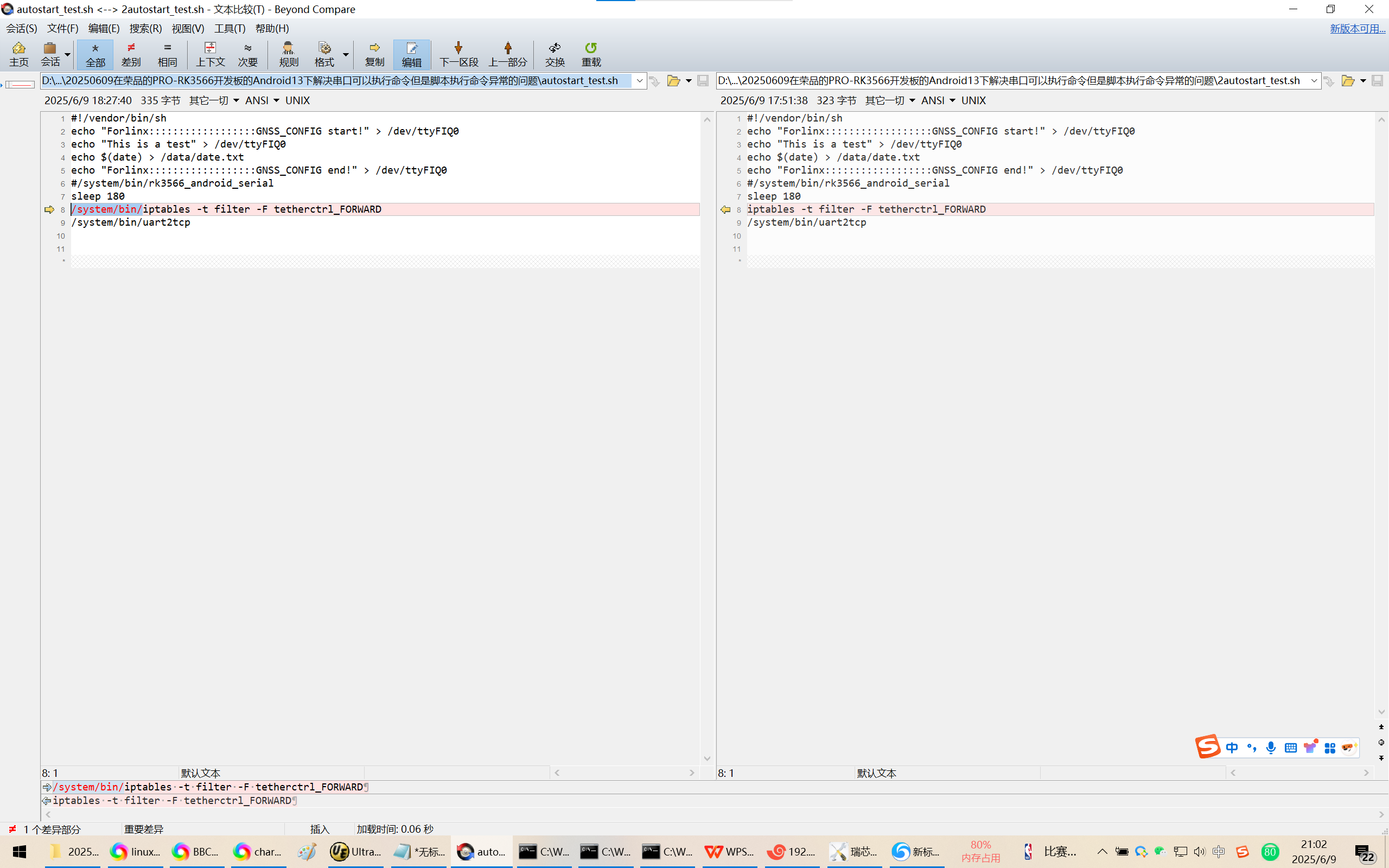
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题 2025/6/9 20:54 缘起,为了跨网段推流,千辛万苦配置好了网络参数。 但是命令iptables -t filter -F tetherctrl_FORWARD可以在调试串口/DEBUG口正确执行。…...