分类算法系列⑤：决策树

目录

1、认识决策树

2、决策树的概念

3、决策树分类原理

基本原理

数学公式

4、信息熵的作用

5、决策树的划分依据之一：信息增益

5.1、定义与公式

5.2、⭐手动计算案例

5.3、log值逼近

6、决策树的三种算法实现

7、API

8、⭐两个代码案例

8.1、决策树分类鸢尾花数据集

流程：

代码：

代码解释：

结果

决策树

8.2、泰坦尼克号乘客生存预测

泰坦尼克号数据

分析

代码

代码解释

结果

决策树

8.3、⭐如何可视化dot文件

9、总结

---

 🍃作者介绍：双非本科大三网络工程专业在读，阿里云专家博主，专注于Java领域学习，擅长web应用开发、数据结构和算法，初步涉猎Python人工智能开发。

🦅主页：@逐梦苍穹

⭐分类算法系列①：初识概念

⭐分类算法系列②：KNN(K-近邻)算法

⭐分类算法系列③：模型选择与调优 (Facebook签到位置预测)

⭐分类算法系列④：朴素贝叶斯算法

🍁您的三连支持，是我创作的最大动力🌹

1、认识决策树

决策树思想的来源非常朴素，程序设计中的条件分支结构就是if-then结构，最早的决策树就是利用这类结构分割数据的一种分类学习方法。

怎么理解这句话？通过一个对话例子：

​

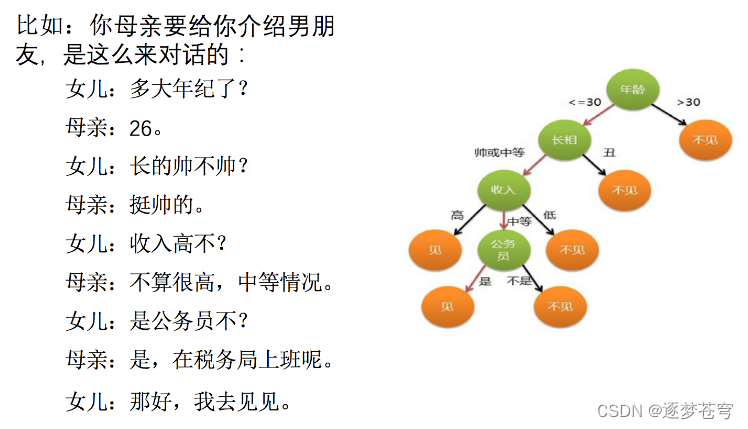
想一想这个女生为什么把年龄放在最上面判断？这就是涉及到决策树的效率

2、决策树的概念

决策树是一种广泛应用于机器学习和数据挖掘领域的监督学习算法，用于分类和回归任务。它是一种基于树状图结构来做出决策的模型，非常直观且易于解释。在决策树中，每个内部节点表示一个属性或特征，每个分支代表一个属性测试，每个叶子节点表示一个类别标签或回归值。以下是决策树的关键概念和特点：

1. 树状结构：决策树采用树状结构，其中根节点表示整个数据集，内部节点表示属性或特征，叶子节点表示类别或回归值。每个节点可以有多个子节点，但通常不会太深，以避免过度拟合。
2. 分裂节点：决策树的构建过程涉及选择一个属性或特征，将数据集分成不同的子集。这个过程持续递归地进行，直到满足停止条件。
3. 属性选择：在每个内部节点，决策树算法会选择一个最佳属性或特征来进行数据分割。常见的属性选择方法包括信息增益、基尼不纯度和均方误差。
4. 剪枝：决策树容易过度拟合训练数据，为了避免这种情况，可以采用剪枝策略。剪枝是删除某些子树或叶子节点，以简化模型并提高泛化能力。
5. 分类与回归：决策树可用于分类问题和回归问题。在分类问题中，叶子节点表示类别标签。在回归问题中，叶子节点表示一个数值。
6. 特征重要性：决策树可以提供特征重要性的信息，即哪些特征对于分类或回归任务更为关键。这可以帮助特征选择和理解数据。
7. 解释性：决策树模型具有很高的解释性，因为它们的决策过程可以直观地表示为一系列的规则。这使得决策树在需要解释机器学习模型决策的情况下非常有用。
8. 容易过拟合：决策树在训练数据上容易过拟合，因此常常需要剪枝等正则化方法来降低模型复杂度。

决策树的一些常见变体包括随机森林（通过多个决策树进行集成）、梯度提升树（通过迭代建立多个决策树），以及CART（分类与回归树）等。

决策树在许多领域都有广泛的应用，包括医疗诊断、金融风险评估、自然语言处理、图像处理等。它们的优点包括易于理解、易于可视化、高效计算和适用于各种数据类型。但需要注意的是，决策树可能对数据中的噪声敏感，并且可能需要进一步的处理来提高性能。

3、决策树分类原理

基本原理

决策树分类原理是一种基于树状结构的监督学习算法，用于解决分类问题。其基本原理涉及将数据分成不同的类别，以构建树状结构，使决策树能够对新数据进行分类。下面是决策树分类的基本原理：

1. 初始节点：决策树的根节点包含整个训练数据集。初始时，所有训练样本都属于同一个类别或标签。
2. 属性选择：选择一个最佳属性或特征来进行数据分割。这个选择通常基于某个属性的判别能力，目标是将数据分成尽可能纯净的子集。不纯度的度量方式有多种，包括信息增益、基尼不纯度和均方误差等。选择属性的过程可以看作是在节点上进行一个属性测试，例如，如果某个特征的值大于某个阈值，则分到左子树，否则分到右子树。
3. 分裂节点：根据选择的属性，将数据集分成多个子集，每个子集对应一个分支。这些分支成为决策树的内部节点。
4. 递归构建：重复上述过程，对每个内部节点递归地选择最佳属性，并分割数据，直到满足停止条件。停止条件可以是树达到最大深度、节点包含的样本数小于某个阈值、或者数据集在某个节点上已经完全纯净（所有样本属于同一类别）。
5. 叶子节点：当决策树构建完成后，所有终止分裂的节点称为叶子节点。叶子节点包含一个类别或标签，表示在该节点上的样本属于该类别。
6. 分类：对于新的数据点，从根节点开始，根据每个节点上的属性测试，沿着适当的分支移动，直到达到叶子节点。最终的叶子节点的类别即为决策树对新数据点的分类结果。

总的来说，决策树分类的原理是通过递归地选择属性并分裂数据，构建一个树状结构，使得每个叶子节点代表一个类别。这样，当新的数据点到达树的叶子节点时，可以根据叶子节点的类别标签来进行分类预测。决策树分类具有直观性、易解释性和适用性广泛的特点，但需要小心处理过拟合问题，通常需要剪枝等正则化技术。

数学公式

决策树分类的数学原理涉及到属性选择和分割数据的数学方法，以及如何确定叶子节点的类别。以下是决策树分类的主要数学原理：

①信息熵（Entropy）：信息熵是一个用于度量数据不纯度或混乱程度的概念。

对于一个二分类问题，信息熵的计算公式如下：

其中，H(X) 表示数据集 X 的信息熵，c 表示类别的数量，pi 表示第 i 个类别在数据集中的占比。信息熵越高，表示数据集越不纯。

②条件熵：

（ 表示属于某个类别的样本数）

③信息增益（Information Gain）：信息增益是衡量在选择某个属性后信息熵减少的程度。

在决策树中，选择信息增益最大的属性来进行分割。

信息增益的计算公式如下：

其中，X 表示当前节点的数据集，A 表示属性，Values(A) 表示属性 A 可能的取值，Xv 表示属性A 取值为v时的数据子集。

④基尼不纯度（Gini Impurity）：基尼不纯度是另一种用于度量数据不纯度的指标。

对于一个二分类问题，基尼不纯度的计算公式如下：

其中，Gini(X) 表示数据集 X 的基尼不纯度，c 表示类别的数量，pi 表示第 i 个类别在数据集中的占比。

基尼不纯度越低，表示数据集越纯。

⑤基尼增益（Gini Gain）：基尼增益是衡量在选择某个属性后基尼不纯度减少的程度。

公式：

在决策树中，选择基尼增益最大的属性来进行分割。基尼增益的计算公式与信息增益类似，但使用基尼不纯度来度量。

⑥决策树构建过程：决策树的构建过程是通过递归选择最佳属性来分割数据集，直到满足停止条件。通常，停止条件包括树达到最大深度、节点包含的样本数小于某个阈值，或者数据集在某个节点上已经完全纯净（所有样本属于同一类别）。

⑦剪枝（Pruning）：决策树容易过拟合训练数据，为了避免过拟合，可以采用剪枝策略。剪枝是删除某些子树或叶子节点，以简化模型并提高泛化能力。常见的剪枝方法包括预剪枝和后剪枝。

总的来说，决策树分类的数学原理涉及使用信息熵、信息增益、基尼不纯度和基尼增益等指标来选择最佳属性进行数据分割，并通过递归构建树状结构来实现分类。这些指标和方法帮助决策树在数据集中找到最佳的属性

4、信息熵的作用

信息熵在信息理论和机器学习中有着重要的作用，主要体现在以下几个方面：

1. 度量信息不确定性： 信息熵用来度量一个随机变量或数据集的信息不确定性。信息熵越高，表示不确定性越大，反之亦然。在机器学习中，我们经常使用信息熵来衡量数据集的纯度或不纯度。例如，在决策树中，我们选择属性进行划分时通常希望子集的信息熵尽可能低，从而提高分类的准确性。
2. 特征选择： 在特征工程中，我们可以使用信息熵来衡量不同特征对目标变量的贡献。选择具有高信息熵的特征意味着这些特征包含更多关于目标变量的信息，因此可能更有用于建立模型。
3. 决策树构建： 决策树算法中的属性选择依赖于信息熵。通过计算每个属性的信息增益或信息增益比，决策树可以选择最优的属性来进行数据集的划分，从而构建出具有良好泛化性能的决策树模型。
4. 编码与压缩： 在信息编码和数据压缩中，信息熵有助于设计高效的编码方案。香农编码就是一种基于信息熵的数据压缩方法，它能够实现最短的编码长度，以便节省存储空间和传输带宽。
5. 随机事件分析： 在概率论和统计学中，信息熵用于描述随机事件的不确定性或信息量。它是衡量信息的一种重要指标，可用于研究随机事件的性质和分布。

总之，信息熵是一个重要的概念，它帮助我们理解和处理信息的不确定性，对于数据分析、模型构建和信息处理等领域都具有广泛的应用价值。

5、决策树的划分依据之一：信息增益

5.1、定义与公式

特征A对训练数据集D的信息增益g(D,A)，定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差。

即公式为：

带入前面提到的公式，则为：

用通俗的话来说，就是：当知道了某一个特征之后，对于某一事件的不确定性减少了，即信息熵减少了，则称为信息增益。

5.2、⭐手动计算案例

下面的案例是一个贷款案例，给定多个特征，判断是否贷款的可能性：

数据情况如下：

​

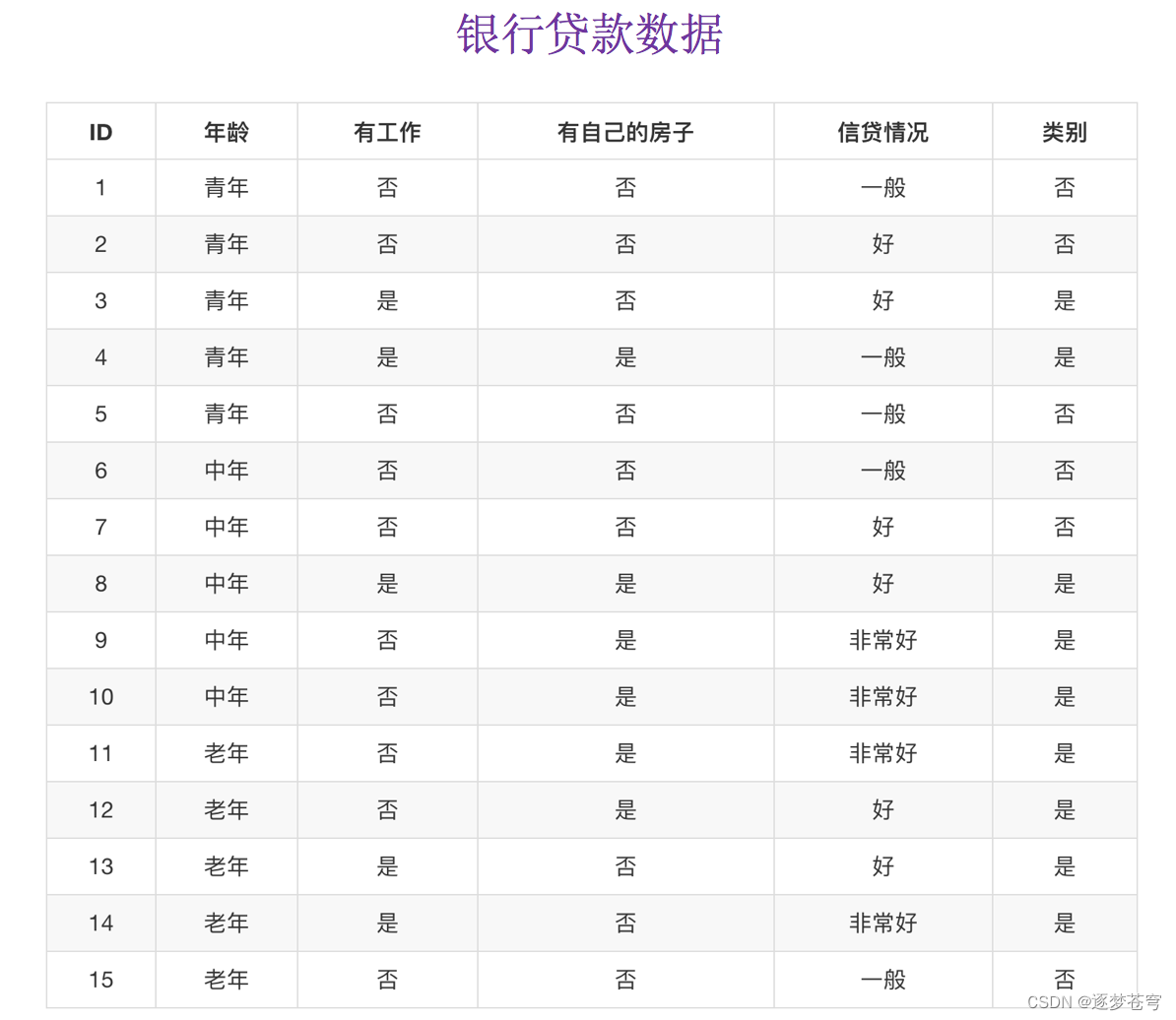
下面是具体的计算，需要计算出决策树的根节点，即“知道了哪一个特征之后，对于是否贷款的问题，减少了最多的不确定性”。

总的信息熵为"是/否"：

下面是条件熵：

①条件为"知道年龄"这一特征：

即

青年：

中年：

老年：

②条件为"知道是否有工作"这一特征：

即

③条件为"知道是否有房子"这一特征：

即

④条件为"知道信贷情况"这一特征：

即

根据"青年"的过程，以此类推，最终得出信息增益g(D,A)最高的是（条件为"知道是否有房子"这一特征），所以就把判断是否有房子，作为决策树的根节点，树以此延申。

5.3、log值逼近

对数的基本性质：

如果想要具体的值，可以用泰勒公式或麦克劳林展开式：

泰勒公式：

麦克劳林公式：

的泰勒公式和麦克劳林公式如下：

6、决策树的三种算法实现

决策树是一种常用的机器学习算法，用于分类和回归任务。以下是三种常见的决策树算法的实现方式：

1. ID3（Iterative Dichotomiser 3）算法：ID3算法是决策树的早期算法，主要用于分类任务。它基于信息熵来选择每个节点的划分属性，以最大程度地减少不确定性。以下是ID3算法的关键步骤：
   • 计算每个属性的信息增益。
   • 选择信息增益最高的属性作为划分属性。
   • 递归地构建树，直到满足终止条件（例如，达到叶子节点或最大深度）。
2. C4.5算法：C4.5算法是ID3算法的改进版本，它可以用于分类和回归任务。与ID3不同，C4.5使用信息增益比来选择最佳的划分属性。以下是C4.5算法的关键步骤：
   • 计算每个属性的信息增益比。
   • 选择信息增益比最高的属性作为划分属性。
   • 处理缺失值。
   • 递归地构建树，直到满足终止条件。
3. CART（Classification and Regression Trees）算法：CART算法是一种多用途的决策树算法，可以用于分类和回归任务。与ID3和C4.5不同，CART使用基尼不纯度来选择最佳的划分属性。以下是CART算法的关键步骤：
   • 计算每个属性的基尼不纯度。
   • 选择基尼不纯度最低的属性作为划分属性。
   • 递归地构建树，直到满足终止条件。

这些是三种常见的决策树算法的基本实现方式。每种算法都有其优点和局限性，选择哪种算法通常取决于具体的问题和数据集。实际应用中，您可以使用机器学习库（如scikit-learn）中提供的现成实现来构建决策树模型。在使用这些库时，您可以轻松选择算法，并进行参数调整以获得最佳性能。

7、API

class sklearn.tree.DecisionTreeClassifier(criterion='gini', max_depth=None,random_state=None)

决策树分类器

criterion：默认是'gini'系数，也可以选择信息增益的熵'entropy'

max_depth：树的深度大小

random_state：随机数种子

其中会有些超参数：max_depth:树的深度大小

其它超参数会结合随机森林讲解

8、⭐两个代码案例

8.1、决策树分类鸢尾花数据集

流程：

①获取数据集

②划分数据集

③决策树预估器

④模型评估：对比真实值和预测值，计算准确率

⑤可视化

代码：

# -*- coding: utf-8 -*-
# @Author:︶ㄣ释然
# @Time: 2023/9/1 23:50
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, export_graphviz'''
class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)决策树分类器criterion:默认是’gini’系数，也可以选择信息增益的熵’entropy’max_depth:树的深度大小random_state:随机数种子其中会有些超参数：max_depth:树的深度大小其它超参数会结合随机森林讲解
'''
def decision_iris():"""用决策树对鸢尾花进行分类:return:"""# 1）获取数据集iris = load_iris()# 2）划分数据集x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)# 3）决策树预估器estimator = DecisionTreeClassifier(criterion="entropy")estimator.fit(x_train, y_train)# 4）模型评估# 方法1：直接比对真实值和预测值y_predict = estimator.predict(x_test)print("y_predict:\n", y_predict)print("直接比对真实值和预测值:\n", y_test == y_predict)# 方法2：计算准确率score = estimator.score(x_test, y_test)print("准确率为：\n", score)# 可视化决策树export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)
if __name__ == '__main__':decision_iris()

代码解释：

1. 从sklearn.datasets中导入load_iris函数，用于加载鸢尾花数据集。
2. 使用load_iris函数加载鸢尾花数据集，并将数据集保存在变量iris中。
3. 使用train_test_split函数将数据集划分为训练集和测试集，并将特征数据存储在x_train和x_test中，将目标数据（标签）存储在y_train和y_test中。random_state参数用于控制随机划分的种子，以确保划分结果可重复。
4. 创建一个决策树分类器（DecisionTreeClassifier），使用信息熵（entropy）作为划分标准（criterion="entropy"）。
5. 使用训练集数据（x_train和y_train）来拟合决策树模型，即训练模型。
6. 使用训练好的模型进行预测，将测试集数据x_test输入模型，得到预测结果，并将预测结果存储在y_predict中。
7. 打印预测结果y_predict以及直接比对真实值和预测值的结果，这里使用了布尔运算符==来比较真实标签和预测标签是否相等，输出一个布尔数组表示每个样本的分类是否正确。
8. 使用模型的score方法计算分类准确率，将测试集数据x_test和真实标签y_test输入模型，得到准确率的评估结果。
9. 最后，使用export_graphviz函数将训练好的决策树可视化，并将可视化结果保存为名为"iris_tree.dot"的文件，以便后续生成决策树的图形化表示。

结果

​

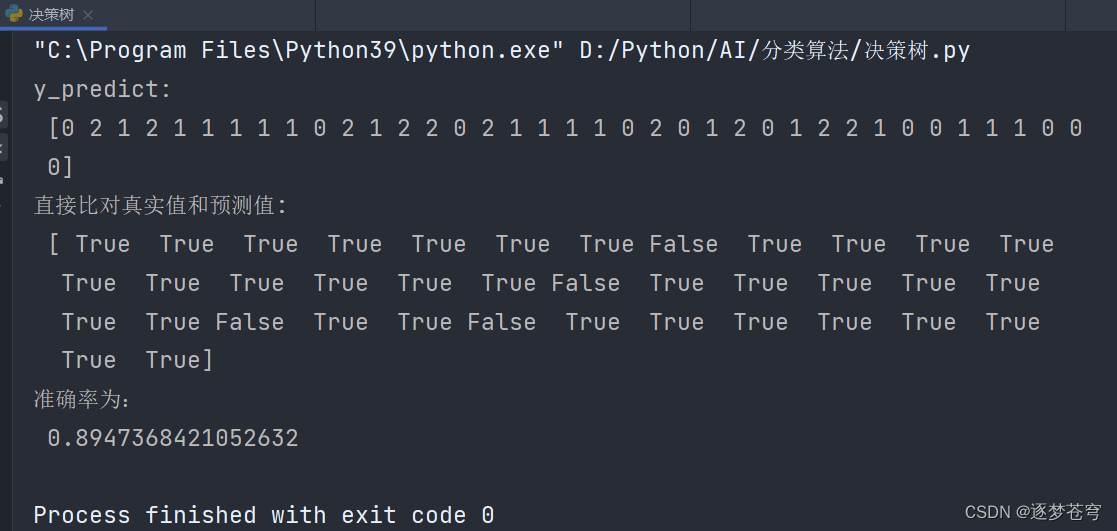
可以看到，同样的鸢尾花数据集预测，使用决策树比之前的KNN算法准确率提高了很多，KNN算法是一种懒算法，不适用于数据量稍大的情景。

决策树

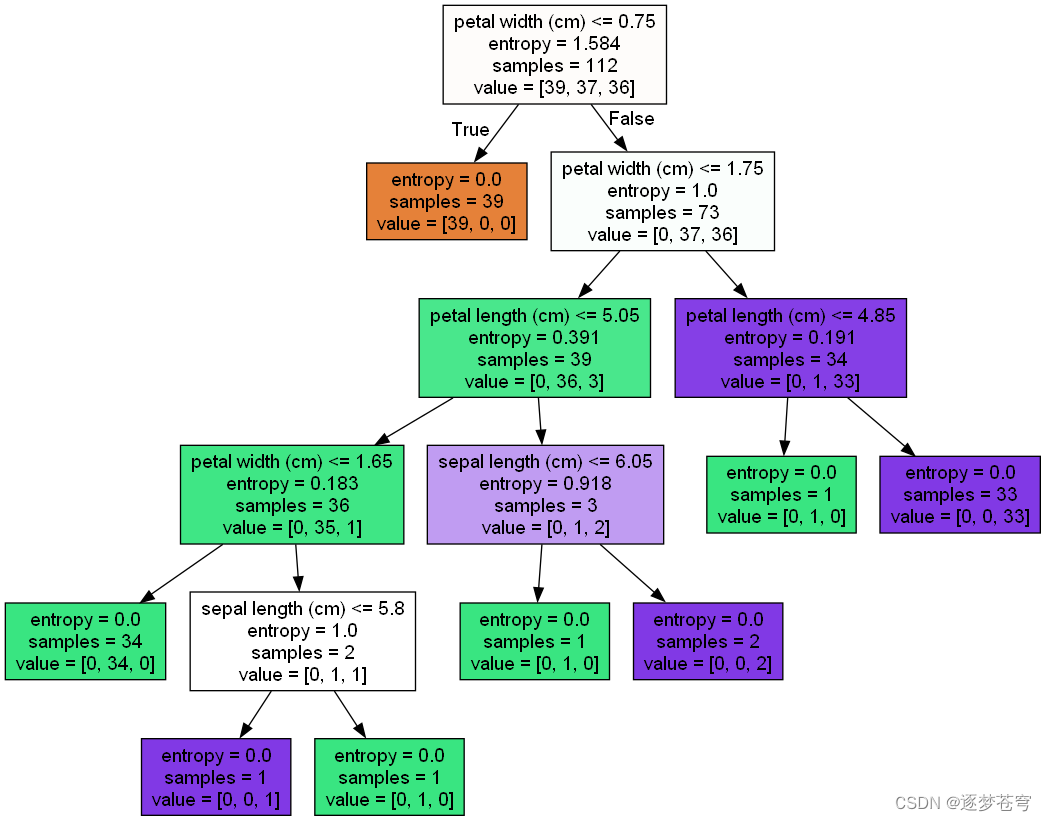
8.2、泰坦尼克号乘客生存预测

泰坦尼克号数据

在泰坦尼克号和titanic2数据帧描述泰坦尼克号上的个别乘客的生存状态。这里使用的数据集是由各种研究人员开始的。其中包括许多研究人员创建的旅客名单，由Michael A. Findlay编辑。我们提取的数据集中的特征是票的类别，存活，乘坐班，年龄，登陆，home.dest，房间，票，船和性别。

数据网址：http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt

如果无法访问，可以访问阿里云的地址：泰坦尼克生存预测数据集_数据集-阿里云天池

完整的数据集文件，也可以在本地找到

分析

选择我们认为重要的几个特征 ['pclass', 'age', 'sex']

填充缺失值

特征中出现类别符号，需要进行one-hot编码处理(DictVectorizer)

x.to_dict(orient="records") 需要将数组特征转换成字典数据

数据集划分

决策树分类预测

代码

# -*- coding: utf-8 -*-
# @Author:︶ㄣ释然
# @Time: 2023/9/1 23:50
import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier'''
class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)决策树分类器criterion:默认是’gini’系数，也可以选择信息增益的熵’entropy’max_depth:树的深度大小random_state:随机数种子其中会有些超参数：max_depth:树的深度大小其它超参数会结合随机森林讲解
'''
def decisioncls():"""决策树进行乘客生存预测"""# 1、获取数据titan = pd.read_csv("./data/titanic/titanic.csv")# 2、数据的处理x = titan[['pclass', 'age', 'sex']]y = titan['survived']# print(x , y)# 缺失值需要处理，将特征当中有类别的这些特征进行字典特征抽取x['age'].fillna(x['age'].mean(), inplace=True)# 对于x转换成字典数据x.to_dict(orient="records")# [{"pclass": "1st", "age": 29.00, "sex": "female"}, {}]dict = DictVectorizer(sparse=False)x = dict.fit_transform(x.to_dict(orient="records"))print(dict.get_feature_names_out())print(x)# 分割训练集合测试集x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)# 进行决策树的建立和预测dc = DecisionTreeClassifier(max_depth=5)dc.fit(x_train, y_train)print("预测的准确率为：", dc.score(x_test, y_test))# 可视化决策树# export_graphviz(dc, out_file="titanic_tree.dot", feature_names=dict.get_feature_names_out())if __name__ == '__main__':decisioncls()# decision_iris()

代码解释

1. 通过pd.read_csv函数从CSV文件中读取泰坦尼克号的数据，并将数据存储在名为titan的Pandas DataFrame中。
2. 从titan中选择特征列'pclass'（船舱等级）、'age'（年龄）、和'sex'（性别）作为模型的输入特征x，并将'survived'（生存情况）列作为模型的目标输出y。
3. 处理缺失值：使用x['age'].fillna(x['age'].mean(), inplace=True)将'age'列中的缺失值用该列的均值填充。
4. 对特征进行字典特征抽取：使用DictVectorizer将特征数据转换为字典数据，并进行独热编码，以便决策树模型能够处理类别型特征。
5. 打印特征列的名称和转换后的特征数据，以查看转换的结果。
6. 使用train_test_split函数将数据集划分为训练集（x_train和y_train）和测试集（x_test和y_test）。
7. 创建决策树分类器对象dc，设置最大深度为5。
8. 使用训练数据x_train和y_train来训练决策树分类器。
9. 使用测试数据x_test和y_test进行生存情况的预测，并计算模型的准确率。
10. 打印模型的预测准确率，即模型在测试集上正确预测的比例。

总结而言，这段代码加载了泰坦尼克号的乘客数据，进行了数据预处理，包括处理缺失值和特征编码，然后使用决策树分类器训练模型，并计算了模型在测试集上的准确率，以评估模型的性能。这是一个典型的机器学习分类问题的实例。

结果

​

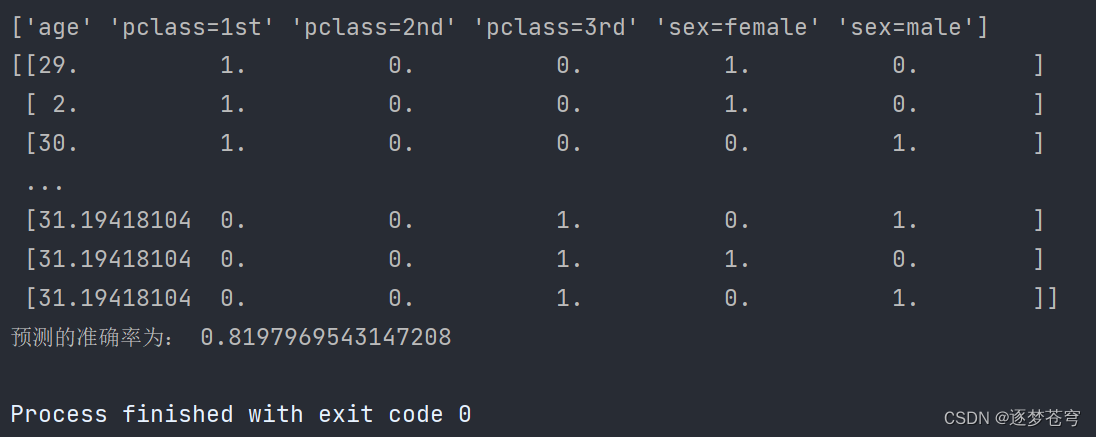
决策树

​

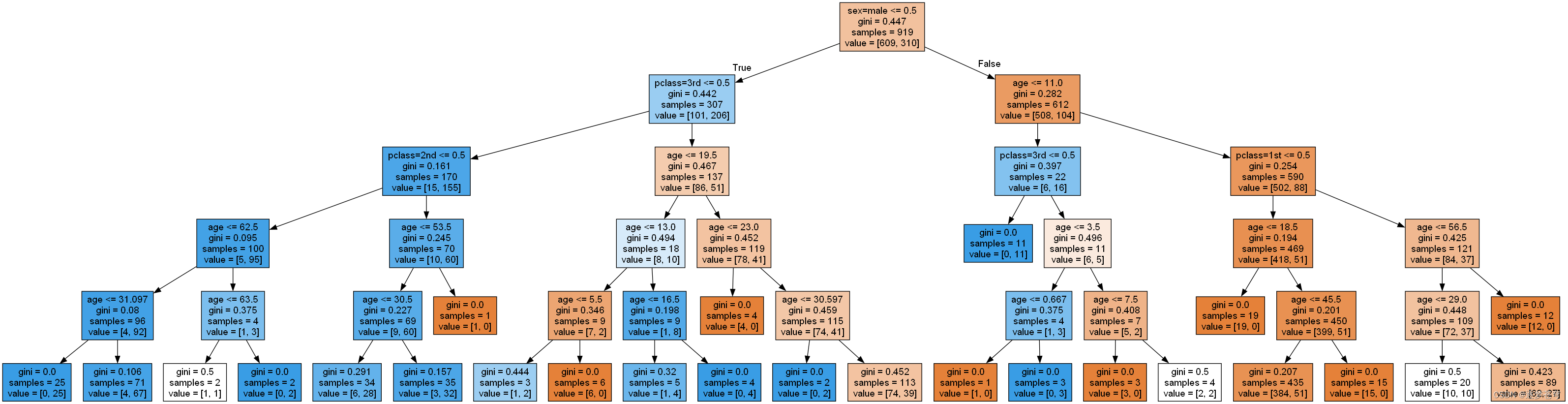
8.3、⭐如何可视化dot文件

工具：(能够将dot文件转换为pdf、png)

安装graphviz：

ubuntu:sudo apt-get install graphviz Mac:brew install graphviz

Windows：下载zip压缩包，解压缩，把bin路径添加到系统环境变量

Windows终端运行命令：dot -Tpng tree.dot -o tree.png

上面得到的是黑白的可视化，如果想要彩色的，则需要调整一下参数：

9、总结

优点：简单的理解和解释，树木可视化。

缺点：决策树学习者可以创建不能很好地推广数据的过于复杂的树，这被称为过拟合。

改进：减枝cart算法(决策树API当中已经实现，随机森林参数调优有相关介绍)

随机森林

注：企业重要决策，由于决策树很好的分析能力，在决策过程应用较多， 可以选择特征