【算法基础】一维差分 + 二维差分

👦个人主页:Weraphael
✍🏻作者简介:目前正在学习c++和算法
✈️专栏:【C/C++】算法
🐋 希望大家多多支持,咱一起进步!😁
如果文章有啥瑕疵
希望大佬指点一二
如果文章对你有帮助的话
欢迎 评论💬 点赞👍🏻 收藏 📂 加关注😍
回顾
- 一维前缀和 + 二维前缀和
目录
- 回顾
- 一、一维差分
- 1.1 什么是差分
- 1.2 如何构造`b`数组
- 1.3 用途
- 1.4 代码
- 模板1
- 模板2 + 解释
- 二、二维差分
- 2.1 什么是二维差分
- 2.2 如何构建`b[i][j]`以及用途
- 2.3 代码模板
- 三、总结
一、一维差分
1.1 什么是差分
- 首先有一个原数组
a:a[1],a[2],a[3] ... a[N] - 然后构造一个数组
b:b[1],b[2],b[3]...b[N],使得a[N] = b[1] + b[2]+ b[3] + ... + b[N] - 所以,我们就称a数组是b数组的前缀和,而
b数组就称为a数组的差分
1.2 如何构造b数组
可以利用高中的知识:
一开始初始化a[0] = 0
b[1] = a[1] - a[0]
b[2] = a[2] - a[1]
b[3] = a[3] - a[2]
…
b[n] = a[n] - a[n-1]
最后再把上述式子加起来,就可以得到:a[n] = b[1] + b[2]+ b[3] + ... + b[n],所以,构造b[n]数列的公式为:b[n] = a[n] - a[n-1]
1.3 用途
假设现在有一问题:将
a数组[l,r]区间中的每一个数都加一常数C,即a[l] + c,a[l+1] + c + ... + a[r] + c(减上一个常数c也是同一个意思)
- 暴力
for循环遍历
[l,r],时间复杂度是O(n)
- 差分
因为
a数组是b数组的前缀和:a[n] = b[1] + b[2] + b[3] + ... + b[n],只要b[l] + c,a数组在区间[l,n]都会加上c,即a[l] + c,a[l + 1] + c,...,a[n] + c,什么意思呢?画个图就豁然开朗了(如下图)
但是,a数组在区间
[l,n]都会加上c,而我们只想在[l,r]上加上c,所以数组b区间[r+1,n]每个数都要-c
一维差分总结:
- 给区间
[l,r]中的每个数加上c,b[l] += c,b[r+1] -= c,并且时间复杂度是O(1)- 下标为什么从1开始其实和前缀和是一个意思 -> 传送门
1.4 代码
模板1
#include <iostream>
using namespace std;const int N = 10010;int a[N],b[N];///全局变量,初始化为0int main()
{int n;// n - 数组元素个数scanf("%d",&n);//输入原数组afor (int i = 1;i <= n;i++) scanf("%d", &a[i]);//构建b数组for (int i = 1;i <= n;i++)b[i] = a[i] - a[i - 1];//a数组在[l,r]上,加上一个数int l,r,c;scanf("%d%d%d",&l,&r,&c);b[l] += c;b[r + 1] -= c;//求出+c后的数组for (int i = 1;i <= n;i++)b[i] = b[i - 1] + b[i];//a[i] = b[i] + a[i - 1]//输出for(int i = 1;i <= n;i++)printf("%d ",b[i]);return 0;
}
模板2 + 解释
#include <iostream>
using namespace std;const int N = 10010;int a[N],b[N];//全局变量,初始化为0void insert(int l,int r,int c)
{b[l] += c;b[r + 1] -= c;
}int main()
{int n;scanf("%d",&n);//输入原数组afor (int i = 1;i <= n;i++) scanf("%d", &a[i]);//构建b数组for (int i = 1;i <= n;i++)insert(i,i,a[i]);//a数组在[l,r]上,加上一个数int l,r,c;scanf("%d%d%d",&l,&r,&c);insert(l,r,c);//求出+c后的数组(前缀和)for (int i = 1;i <= n;i++)b[i] = b[i] + b[i - 1];//a[i] = b[i] + a[i - 1]//输出for(int i = 1;i <= n;i++)printf("%d ",b[i]);return 0;
}
解释:
首先封装了insert函数来帮助我们在某段区间加上c,而为什么构造b数组时也能使用这个函数呢?这个问题其实我也想了很久,但是其实画个图就明白了
二、二维差分
2.1 什么是二维差分
- 首先有一个原数组
a[i][j] - 然后构建一个差分数组
b[i][j],即a[n][m] = b[1][1] + b[2][1] + b[2][2] + ... + b[n][m] - 所以,我们称
a[i][j]是b[i][j]的前缀和数组,而b数组就是a数组的差分
2.2 如何构建b[i][j]以及用途
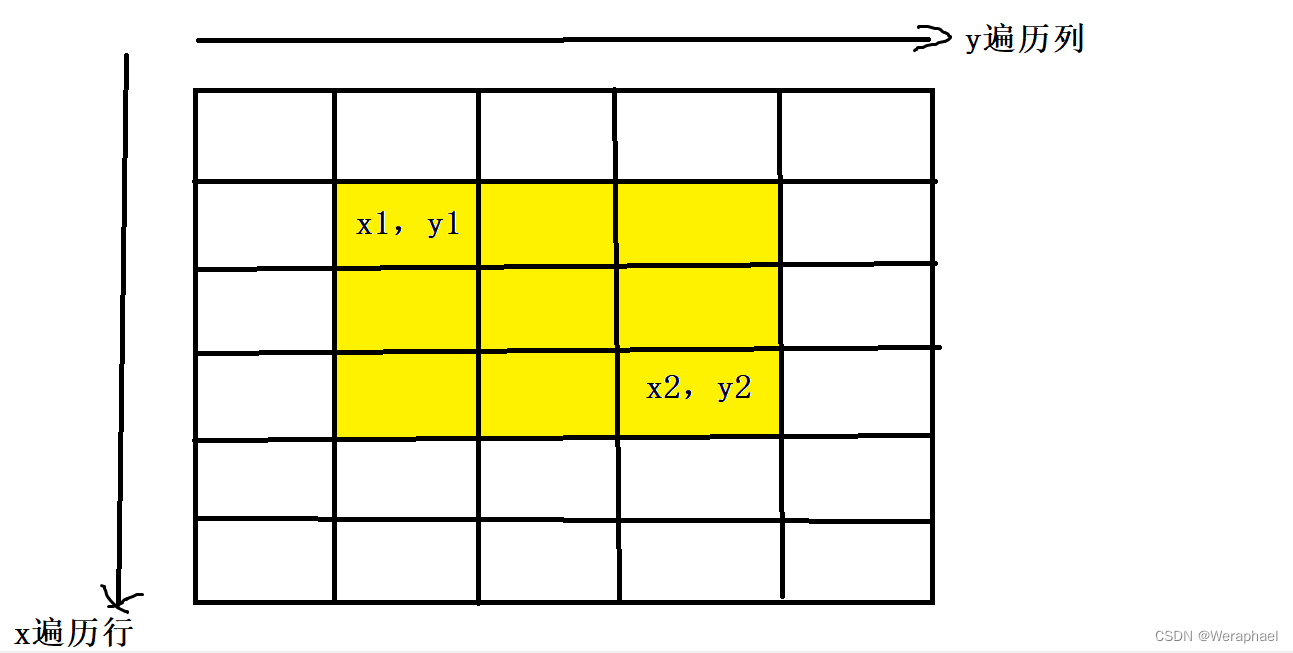
首先先讲讲用途,假设现在有一问题:已知原数组a中被选中的子矩阵是以(x1,y1)为左上角,以(x2,y2)为右下角所围成的区域,现要求在子矩阵中每个数+c
- 暴力做法
for循环遍历,时间复杂度是O(n2)
- 差分
一定要记住,
a数组是b数组的前缀和,若对b数组的b[i][j]的修改,势必会影响到a数组中从a[i][j]及往后的每一个数,时间复杂度可以由O(n2)优化成O(1)
做法如下
目的:让黄色区域所有数都加上c
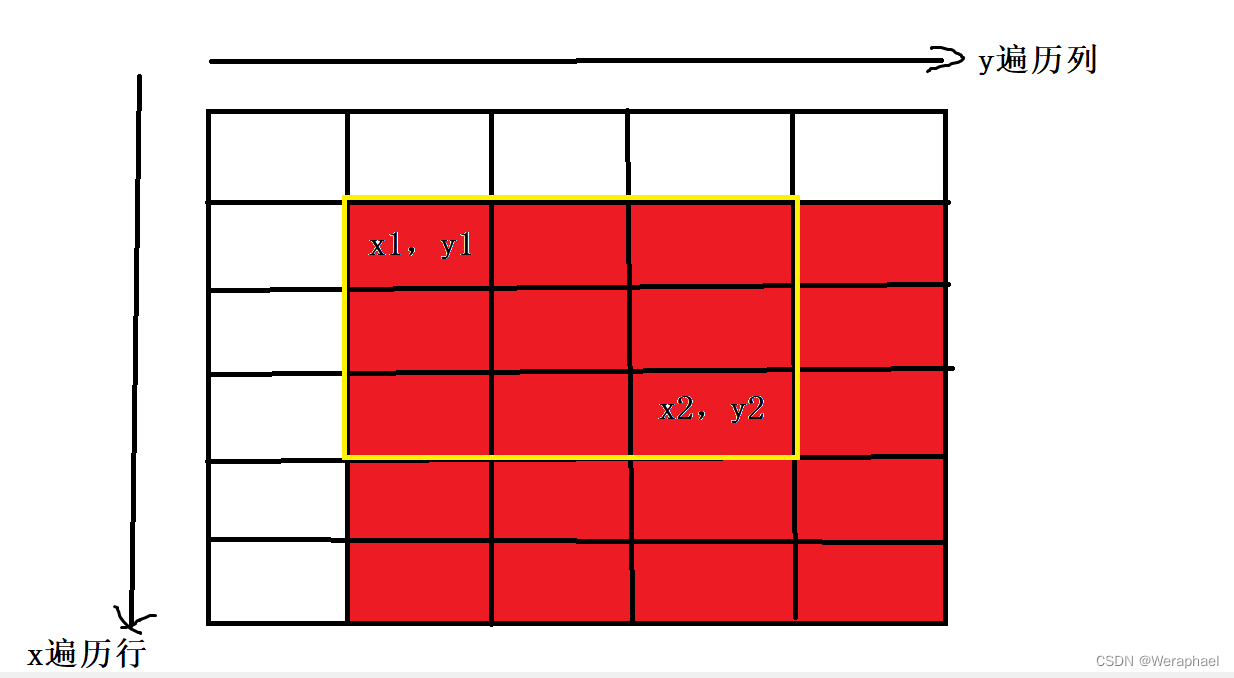
记住,a数组是b数组的前缀和,若对b数组加上c,势必会影响c。所以b[x1][y1]+c,会导致红色区域加上c
所以,现只要把绿色部分多加的c去掉即可
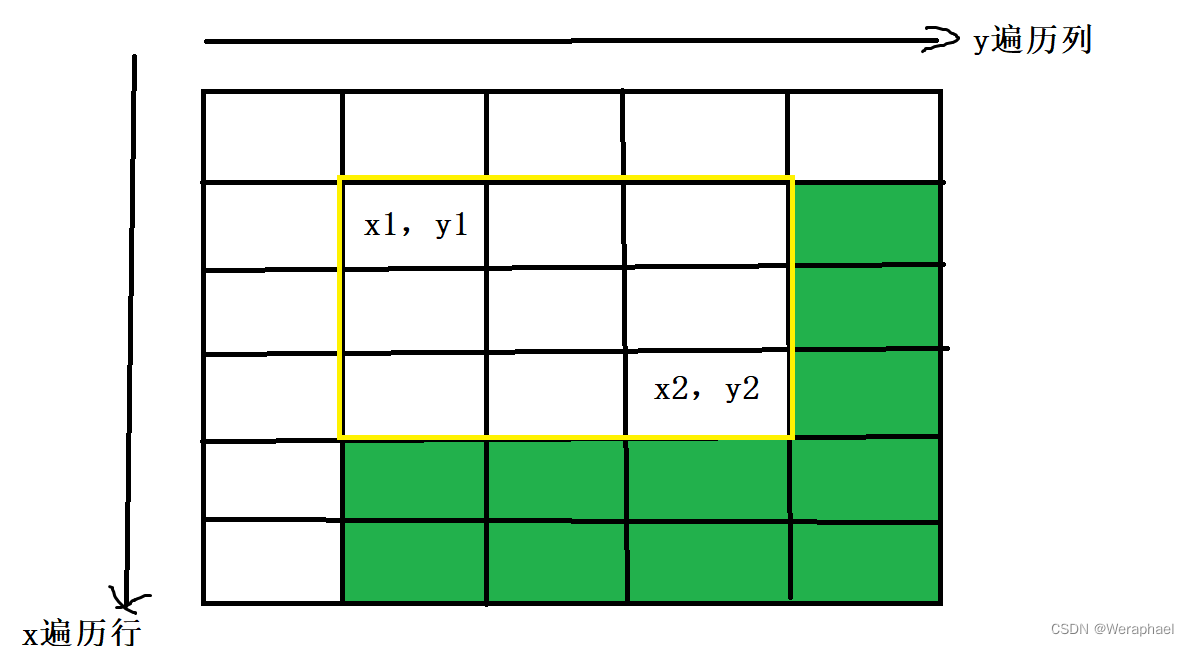
首先,先减去紫色部分多加的c
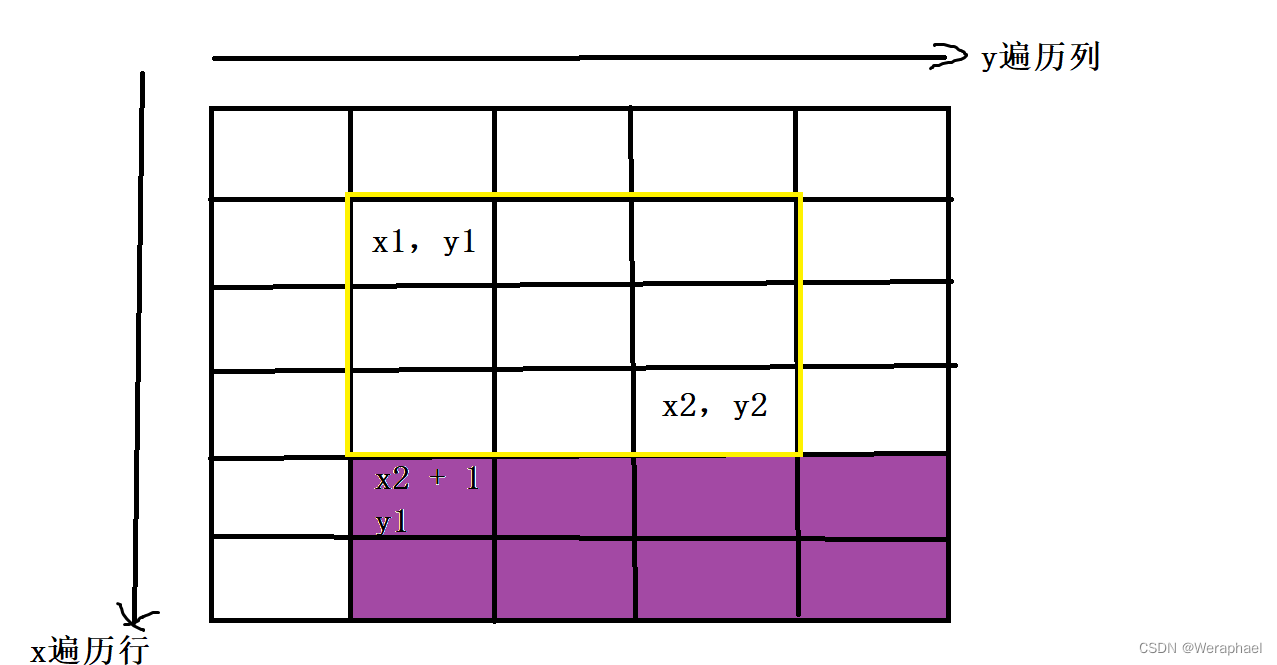
b[x2 + 1][y1] -= c
接下来再减去灰色部分多加的c
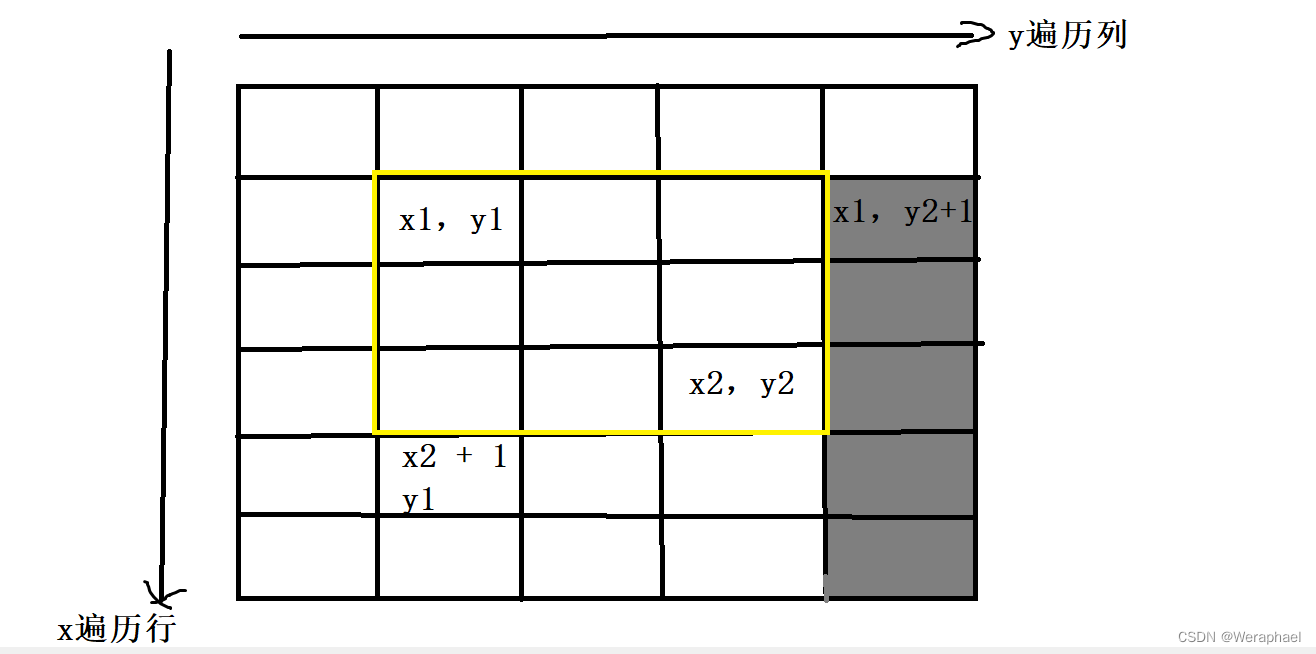
b[x1][y2 + 1] -= c
最后,由于前两步多减了橙色部分的c,所以还要再加回去
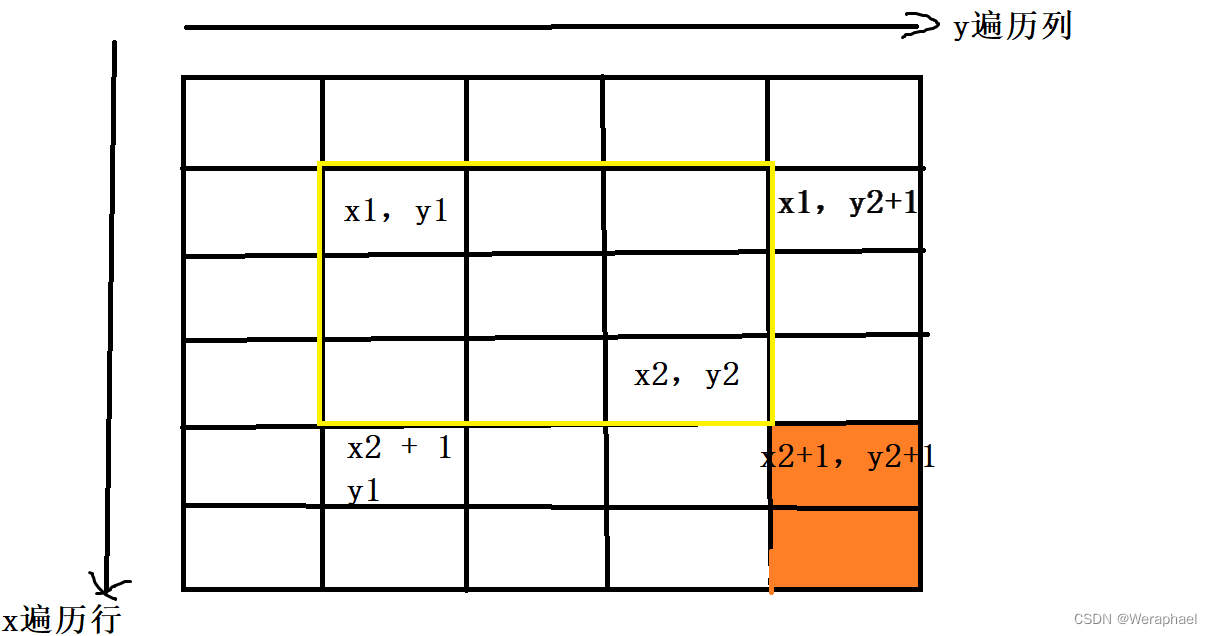
b[x2 +1 ][y2 + 1] += c
我们把上述过程封装成一个insert函数
void insert(int x1,int y1,int x2,int y2,int c)
{ b[x1][y1] += c;b[x2+1][y1] -= c;b[x1][y2+1] -= c;b[x2+1][y2+1] += c;
}
最后b数组的构造也能使用这个插入函数,过程和一维差分差不多,详情请看一维差分的模板2
2.3 代码模板
#include <iostream>
using namespace std;const int N = 10010;int a[N][N],b[N][N];//插入函数
void insert(int x1,int y1,int x2,int y2,int c)
{b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}int main()
{int n,m;scanf("%d%d%d",&n,&m);//输入原数组a + 构造差分数组bfor (int i = 1;i <= n;i++){for (int j = 1;j <= m;j++){scanf("%d",&a[i][j]);insert(i,j,i,j,a[i][j]);}}//在指定子矩阵+cint x1,y1,x2,y2,c;cin >> x1 >> y1 >> x2 >> y2 >> c;insert(x1,y1,x2,y2,c);//二维前缀和for (int i = 1;i <= n;i++){for (int j = 1;j <= m;j++){b[i][j] += b[i-1][j] + b[i][j-1] - b[i-1][j-1];}}for (int i = 1;i <= n;i++){for (int j = 1;j <= m;j++)printf("%d ",b[i][j]);printf("\n");}return 0;
}三、总结
一维差分
void insert(int l,int r,int c)
{b[l] += c;b[r + 1] -= c;
}
二维差分
void insert(int x1,int y1,int x2,int y2,int c)
{b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}
相关文章:

【算法基础】一维差分 + 二维差分
👦个人主页:Weraphael ✍🏻作者简介:目前正在学习c和算法 ✈️专栏:【C/C】算法 🐋 希望大家多多支持,咱一起进步!😁 如果文章有啥瑕疵 希望大佬指点一二 如果文章对你有…...

游戏服务器框架 技能buff篇
游戏服务器框架 技能buff篇 1.状态 state 全局API 用于定义各种状态检查 bool IsDead(){ // 死亡buff if (buff->id 10001){ return true; } return false; } bool IsInvincible(){ if (buff->id 20001 || buff->id 20002){…...
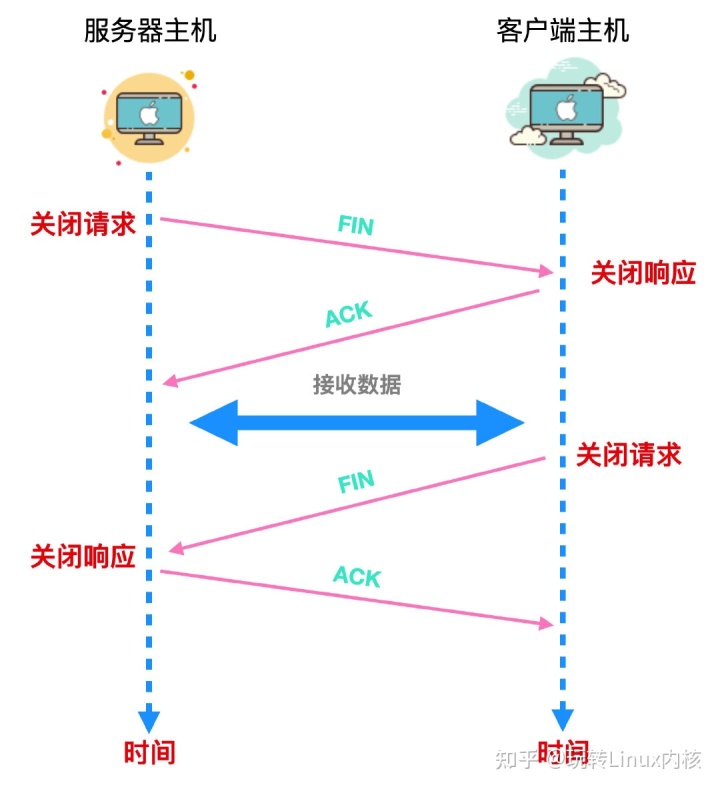
网友说socket通信讲的不彻底,原来这才是Socket
关于对 Socket 的认识,大致分为下面几个主题,Socket 是什么,Socket 是如何创建的,Socket 是如何连接并收发数据的,Socket 套接字的删除等。 Socket 是什么以及创建过程 一个数据包经由应用程序产生,进入到…...
Nginx第二讲
目录 二、Nginx02 2.1 keepalived和heartbeat介绍 2.1.1 两者的介绍 2.1.2 keepalived简介 2.1.3 VRRP协议与工作原理 2.1.4 Keepalvied的工作原理 2.2 安装环境及keepalived 2.3 启动与验证keepalived 2.4 keepalived测试 2.4.1 环境准备 2.4.2 配置keepalived 2.…...
redis(win版)
1. 前言1.1 什么是RedisRedis是一个基于内存的key-value结构数据库。Redis 是互联网技术领域使用最为广泛的存储中间件,它是「Remote Dictionary Service」的首字母缩写,也就是「远程字典服务」。基于内存存储,读写性能高适合存储热点数据&am…...
【Linux】编辑器——vim(最小集+指令集+自动化配置)
目录 1.vim最小集 1.1 vim的三种模式 1.2 vim的基本操作 2.vim指令集 2.1 命令模式指令集 移动光标 删除文字 复制 替换 撤销上一次操作 更改 跳至指定的行 2.2 底行模式指令集 列出行号 跳到文件中的某一行 查找字符 保存文件 多文件操作 3.如何配置vim 配…...

Centos7+Xshell+Jenkins堆装
windows系统崩坏,重装测试类工具,心情崩了 windows硬盘损坏前,运行应用具慢。。。。。。慢着慢着就走了 从前部署在本地的jenkins,python,gitblit等相关脚本都凉透了,所以这次把服务部署到Centos7上…...

Android system实战 — Android R(11) 进程保活白名单
Android system实战 — Android R 进程保活白名单0. 前言1. 具体实现1.1 准备工作1.2 源码实现1.2.1 源码1.2.2 diff文件0. 前言 最近在Android R上实现一些需求,进行记录一下,关于进程保活的基础知识可以参考Android system — 进程生命周期与ADJ&#…...

oracle表 分组,并查每组第一条
oracle主要用到的函数:OVER(PARTITION BY) mysql主要用到的函数:LIMIT (用到3个地方:分组列、组内排序列、表名) oracle: select t.* from ( select a.*, ROW_NUMBER() OVER (PARTITION BY 分组列 ORDER BY 组内排…...
)
Java代码弱点与修复之——DE: Dropped or ignored exception(无视或忽略异常)
弱点描述 Dropped or ignored exception(DE)指的是在代码中抛出的异常被捕获后被无视或忽略了,而不是被适当地处理。这种情况通常发生在程序员没有处理异常或处理异常时不小心忽略了异常的情况下。 Dropped or ignored exception会导致程序无法正常工作,因为异常会阻塞程…...
JavaEE简单示例——动态SQL之更新操作<set>元素
简单介绍: 在之前我们做的学生管理系统的时候,曾经有一个环节是修改学生的数据。我们在修改的时候是必须将student对象的三个属性全部填入信息,然后全部修改才可以,这样会造成一个问题就是在我们明明只需要修改一个属性的时候却要…...
【极海APM32替代笔记】低功耗模式配置及配置汇总
【极海APM32替代笔记】低功耗模式配置及配置汇总 文章总结:(后续更新以相关文章为准) 【STM32笔记】低功耗模式、WFI命令等进入不了休眠的可能原因(系统定时器SysTick一直产生中断) 【STM32笔记】HAL库低功耗模式配置…...

攻击者失手,自己杀死了僵尸网络 KmsdBot
此前,Akamai 的安全研究员披露了 KmsdBot 僵尸网络,该僵尸网络主要通过 SSH 爆破与弱口令进行传播。在对该僵尸网络的持续跟踪中,研究人员发现了一些有趣的事情。 C&C 控制 对恶意活动来说,最致命的就是夺取对 C&C 服务…...

东阿县高新技术企业认定条件和优惠政策 山东同邦科技分享
东阿县高新技术企业认定条件和优惠政策 山东同邦科技分享 高新技术企业 在《国家重点支持的高新技术领域》内,持续进行研究开发与技术成果转化,形成企业核心自主知识产权,并以此为基础开展经营活动,在中国境内(不包…...

【基础算法】哈希表(拉链法)
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...
硬件学习 软件Cadence day07 PCB 底板电路图布线
1.根据原理图的元器件, 选择在 PCB 芯片制作的元器件 (allegro中原理图和pcb中元件的交互) 1.首先完成下列操作 可以尝试先关闭再打开, 等下操作的时候就好 发现新增的发光物体!! 2.完成操作 ,…...

SkyWalking仪表盘使用
Skywalking仪表盘使用 1 仪表盘 作用:查看被监控服务的运行状态。 1)监控面板 1.1 APM APM:应用性能管理,通过各种探针采集数据,收集关键指标,同时搭配数据呈现以实现对应用程序性能管理和故障管理的系统化解决方案…...
面渣逆袭:分布式十二问,万字图文详解
大家好,我是老三,不管今年金三银四如何,面渣逆袭系列继续,这期我们来看看分布式。 分布式理论 1. 说说CAP原则? CAP原则又称CAP定理,指的是在一个分布式系统中,Consistency(一致性…...
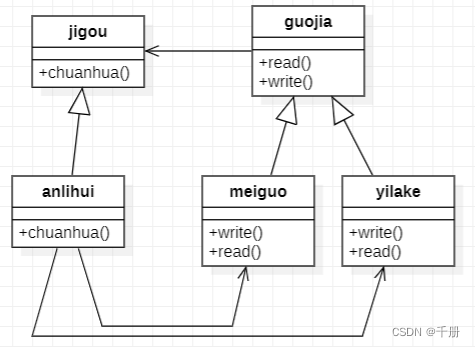
设计模式C++实现23:中介者模式(Mediator)
部分内容参考大话设计模式第25章;本实验通过C语言实现。 一 原理 意图:用一个中介对象来封装一系列对象的交互,中介者使得各个对象不需要显示地相互引用,从而使耦合松散,而且可以独立地改变它们之间的交互。 上下文…...
Java方法【未完待续】
目录 前言 一、什么是方法? 二、方法的定义和调用 方法的定义 方法的调用 三、方法的重载 重载规则 实现理论 总结 前言 随着对Java这一编程语言的深入学习,大家可能会遇到一个熟悉又陌生的词——方法,其实Java方法就是我们学习C/C时…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

大模型——基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程
基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网:https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘,大小大概2.9G,做这行最忌讳的就是安装软件全装C盘,所以我调整了下安装路径。 新建安装目录:E:\MyS…...

__VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.
这个警告表明您在使用Vue的esm-bundler构建版本时,未明确定义编译时特性标志。以下是详细解释和解决方案: 问题原因: 该标志是Vue 3.4引入的编译时特性标志,用于控制生产环境下SSR水合不匹配错误的详细报告1使用esm-bundler…...