可持久化线段树
可持久化线段树
模板
在某一指定版本的单点查,单点修。
开 m m m 棵线段树,每次修改复制后单点修。时间复杂度 O ( m ( n + log n ) ) O(m(n+\log n)) O(m(n+logn)),空间复杂度 O ( n m ) O(nm) O(nm),不如暴力。
每次修改的时候,影响的点是 log n \log n logn 级的,其余点均不受影响。因修改而新建线段树时,可以利用未修改的点,做到 O ( m log n ) O(m \log n) O(mlogn)。
具体实现动态开点即可,空间复杂度 O ( m log n + n ) O(m \log n+n) O(mlogn+n),注意线段树自身的常数。
代码
静态 kth
模板
第 l − 1 , r l-1,r l−1,r 棵线段树形态相同,可以相减得到区间答案。
离散化,二分答案,每次统计区间内小于他的个数。这个过程可以用可持久化线段树实现,时间复杂度 O ( m log 2 n ) O(m \log ^2n) O(mlog2n)。
事实上,这个过程可以做到 O ( m log n ) O(m \log n) O(mlogn)。即查询时,记左子树区间的数量为 L L L。 L ≥ k L \ge k L≥k,则在左子树中继续找第 k k k 大;否则右子树找第 k − L k - L k−L 大。
相关文章:

可持久化线段树
可持久化线段树 模板 在某一指定版本的单点查,单点修。 开 m m m 棵线段树,每次修改复制后单点修。时间复杂度 O ( m ( n log n ) ) O(m(n\log n)) O(m(nlogn)),空间复杂度 O ( n m ) O(nm) O(nm),不如暴力。 每次修改…...

运行 Node.js 与浏览器 JavaScript
浏览器和 Node.js 都使用 JavaScript 软件语言 - 但字面上的运行时环境是不同的。 Node.js(又名服务器端 JavaScript)与客户端 JavaScript 有许多相似之处。它也有很多差异。 尽管两者都使用 JavaScript 作为软件语言,但我们可以重点关注一些关键差异,这些差异使两者之间…...

File类操作
1. 练习一 在当前模块下的 text 文件夹中创建一个 io.txt 文件 import java.io.File; import java.io.IOException;public class Practice1 {public static void main(String[] args) {File file new File("D:\\kaifamiao");File file1 new File(file, "tex…...
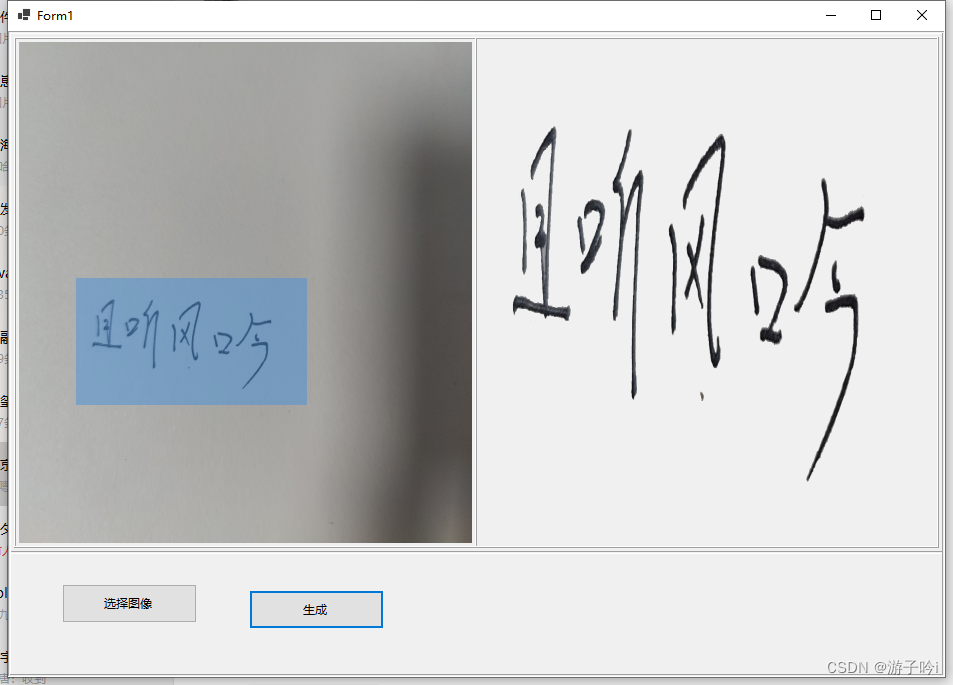
C# 实现电子签名
本项目基于Emgu.CV(C#下OpenCv的封装)开发的,编译器最新版Vs2022,编译环境x86 直接看效果图 1.主页面 2.我们先看手写的方式: 点击确认就到主界面,如下 : 点击自动适配-,再点击生成…...
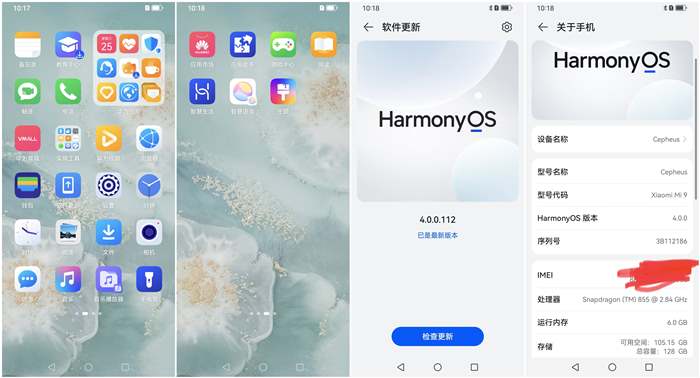
小米6/6X/米8/米9手机刷入鸿蒙HarmonyOS.4.0系统-刷机包下载-遥遥领先
小米手机除了解锁root权限,刷GSI和第三方ROM也是米粉的一大爱好,这不,在华为发布了HarmonyOS.4.0系统后不久,我们小米用户也成功将自己的手机干山了HarmonyOS.4.0系统。虽然干上去HarmonyOS.4.0系统目前BUG非常多,根本…...
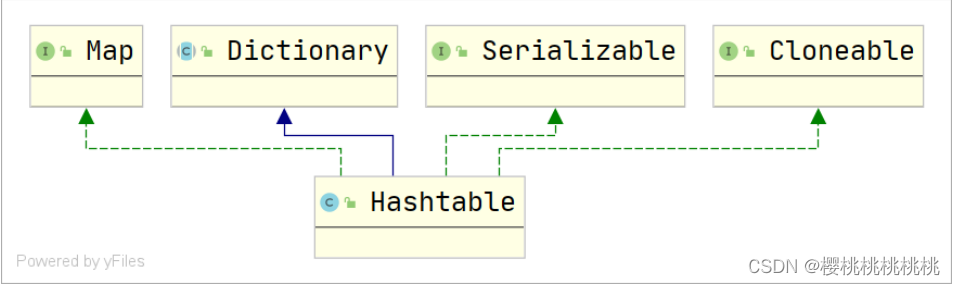
集合框架和泛型二
一、Set接口 1. Set接口概述 java.util.Set 不包含重复元素的集合、不能保证存储的顺序、只允许有一个 null。 public interface Set<E> extends Collection<E>抽象方法,都是继承自 java.util.Collection 接口。 Set 集合的实现类有很多,…...
)
thinkphp6 入门教程合集(更新中)
thinkphp6 入门(1)--安装、路由规则、多应用模式 thinkphp6 入门(1)--安装、路由规则、多应用模式_软件工程小施同学的博客-CSDN博客 thinkphp6 入门(2)--视图、渲染html页面、赋值 thinkphp6 入门&#…...

openGauss学习笔记-65 openGauss 数据库管理-创建和管理数据库
文章目录 openGauss学习笔记-65 openGauss 数据库管理-创建和管理数据库65.1 前提条件65.2 背景信息65.3 注意事项65.4 操作步骤65.4.1 创建数据库65.4.2 查看数据库65.4.3 修改数据库65.4.4 删除数据库 openGauss学习笔记-65 openGauss 数据库管理-创建和管理数据库 65.1 前提…...

mysql、MHA高可用配置即故障切换
MHA概述 一套优秀的MySQL高可用环境下故障切换和主从复制的软件 MHA的出现就是解决MySQL 单点的问题 MySQL故障过程中,MHA能做到0-30秒内自动完成故障切换 MHA能在故障切换的过程中最大程度上保证数据的一致性以达到真正意义上的高可用 MHA的组成(核…...

使用“vue init mpvue/mpvue-quickstart“初始化mpvue项目时出现的错误及解决办法
当使用"vue init mpvue/mpvue-quickstart"初始化 mpvue 项目时出现 "vue-cli Failed to download repo mpvue/mpvue-quickstart: connect ETIMEDOUT IP地址"原因是 github 的 IP 解析失败,连接超时 解决办法:更改最新的 github 的 …...

Linux-Shell整理集合
Shell变量 参考文章: Shell脚本中变量的使用 shell语法之 , ‘ ‘ , {},, ,‘‘,(),$(())四种语法含义 参考文章: shell语法之 , ‘ ‘ , {},, ,‘‘,(),$(())四种语法含义 grep常用用法 Shell awk命令详解 grep 跟awk连着用: 获取某程序的…...

windows环境下node安装教程(超详细)
安装node.js 1、下载node: 下载地址:下载 | Node.js 中文网 node.js的zip包安装时是直接解压缩后就可以了, node.js的msi包是傻瓜式一路next就可以了 选择一中方式就可以 2、解压后的目录,或者mis安装后的目录如下: 3、安装完后,可以在命令行中输入…...
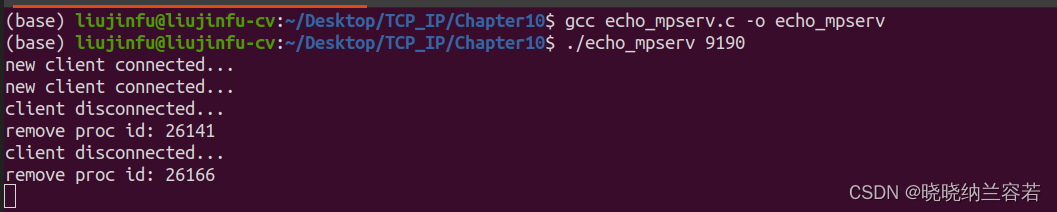
《TCP/IP网络编程》阅读笔记--并发多进程服务端的使用
目录 1--并发服务器端 2--进程 2-1--进程的相关概念 2-2--fork()创建进程 2-3--僵尸进程 2-4--wait()和waitpid()销毁僵尸进程 3--信号处理 3-1--signal()函数 3-2--sigaction()函数 3--3--利用信号处理技术消灭僵尸进程 4--基于多任务的并发服务器 5--分割 TCP 的…...

【C++】day2学习成果:引用、结构体等等。。。
1.封装一个结构体,结构体中包含一个私有数组,用来存放学生的成绩,包含一个私有变量,用来记录学生个数, 提供一个公有成员函数,void setNum(int num)用于设置学生个数 提供一个公有成员函数:void…...
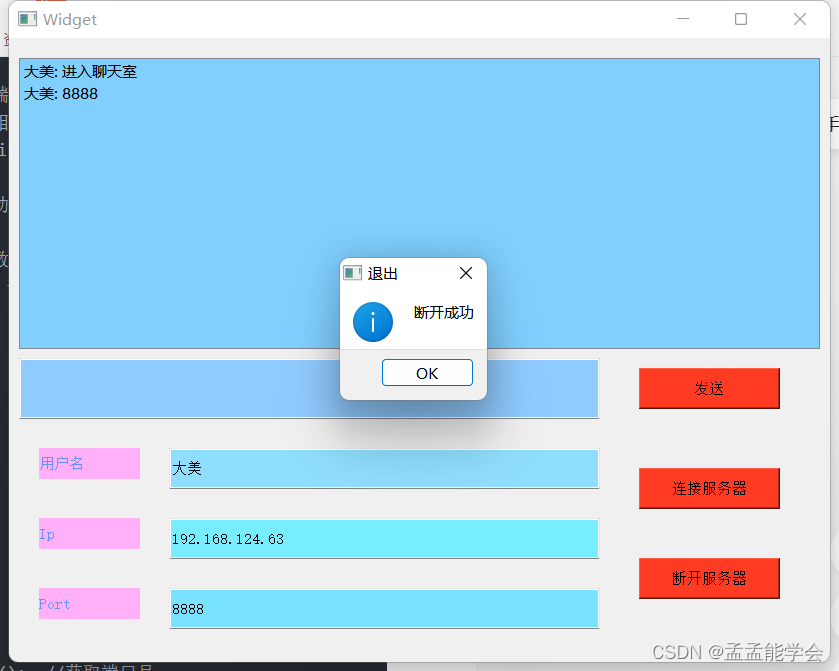
QT 第五天 TCP通信与数据库
一、数据库增删改查 QT core gui sqlgreaterThan(QT_MAJOR_VERSION, 4): QT widgetsCONFIG c11# The following define makes your compiler emit warnings if you use # any Qt feature that has been marked deprecated (the exact warnings # depend on your comp…...

Java程序中常用的设计模式有哪些和该种设计模式解决的痛点
设计模式是大量程序员智慧的结晶,是优秀的代码范式,是以前那些大佬程序员的编程经验总结,非常值得学习。 在软件开发中,有许多常用的设计模式,每种模式都解决了特定类型的问题。以下是一些常见的设计模式及其简要介绍&…...

Android12之解析/proc/pid进程参数(一百六十四)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...
正儿八经的雅思口语盘丝洞大法学习总结(长期修改更新)针对23.9月考生
目录 开篇语 李仙童口语大法 具体体系内容 说道科技产品或者说非传统物品 part2回答八大准则 【part2回答八大准则】(一) 【part2回答八大准则】(二) 【part3回答七大准则】(一) Part 1 核心体系 …...

算法竞赛入门【码蹄集新手村600题】(MT1260-1280)C语言
算法竞赛入门【码蹄集新手村600题】(MT1260-1280)C语言 目录MT1260 袋鼠躲猫猫MT1261 留下来的才是幸运数MT1262 约数MT1263 最大的三位约数MT1264 完数MT1265 区间完数MT1266 完数与因子MT1267 亏数MT1268 因数的因数MT1269 区间素数MT1270 素数计算MT1271 三生质数…...
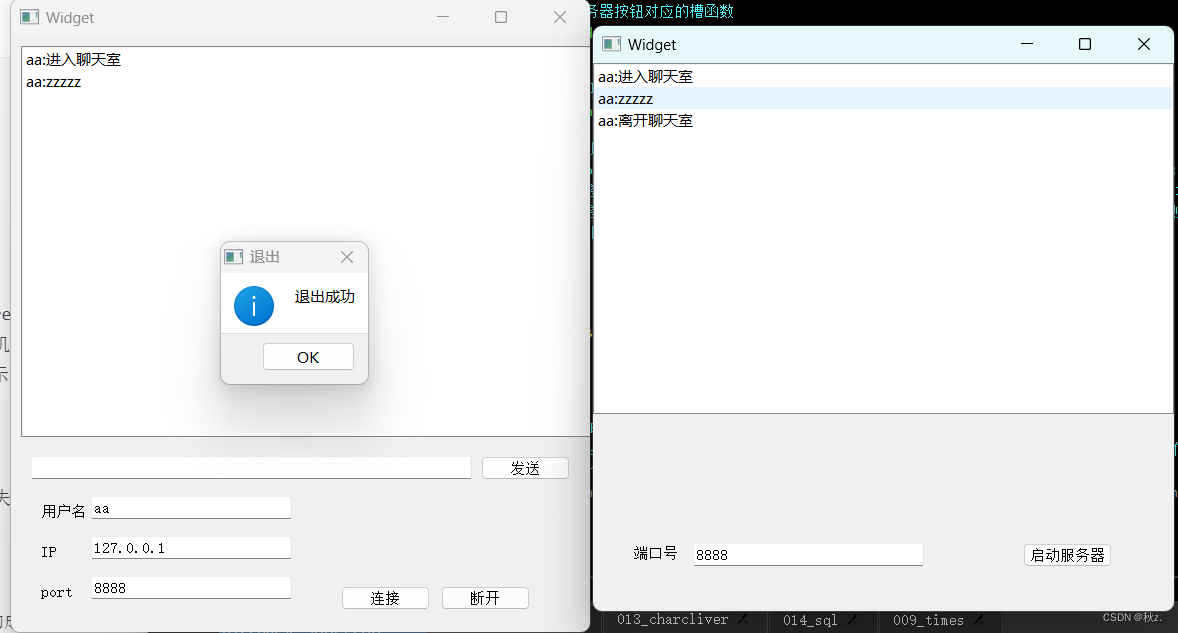
qt连接tcp通信和连接数据库
通过数据库实现学生管理系统 widget.cpp #include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);//判断数据库对象是否包含了自己使用的数据库 Studemt.dbif(!db.co…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
