算法竞赛入门【码蹄集新手村600题】(MT1260-1280)C语言
算法竞赛入门【码蹄集新手村600题】(MT1260-1280)C语言
- 目录
- MT1260 袋鼠躲猫猫
- MT1261 留下来的才是幸运数
- MT1262 约数
- MT1263 最大的三位约数
- MT1264 完数
- MT1265 区间完数
- MT1266 完数与因子
- MT1267 亏数
- MT1268 因数的因数
- MT1269 区间素数
- MT1270 素数计算
- MT1271 三生质数
- MT1272 双素数
- MT1273 N以内双素数
- MT1274 都相差6
- MT1275 都相差10
- MT1276 偶数N
- MT1277 合数世纪
- MT1278 自然数N的立方
- MT1279 危险的粒子
- MT1280 后2位数

码蹄集网站地址:https://www.matiji.net/exam/ojquestionlist
目录
MT1260 袋鼠躲猫猫
(1)题目
两只袋鼠在一个总长L米的圆环上躲猫猫。假定环上某一点为坐标原点0,袋鼠宝宝的出发坐标是x,袋鼠妈妈出发坐标是y,单位是米,宝宝一小时能跳a次,妈妈一小时跳b次,假定他们每一跳的距离都是1米,求多少小时后宝宝和妈妈才能见面。如果无法见面则输出-1。x,y,a,b,L都属于正常int范围。“见面”以每小时结束时刻,两只袋鼠的落点相同为准。
格式
输入格式:
输入5个正整数x,y,a,b,L,空格分隔。其中x不等于y。输出格式:
输出整型
样例1
输入:
1 2 3 4 5输出:
4
(2)参考代码
#include<stdio.h>
int main()
{int x, y, a, b, l, time = 1;scanf("%d %d %d %d %d", &x, &y, &a, &b, &l);if (a == b){printf("-1");return 0;}while ((x + a) % l != (y + b) % l){x = (x + a) % l;y = (y + b) % l;time++;}printf("%d", time);return 0;
}
MT1261 留下来的才是幸运数
(1)题目
首先,删除所有序号能被2整除的项的数,我们就得1,3,5,7,9,11,13,15,17,19…现在,删除所有序号能被3整除的项,我们得到1,3,7,9,13,15,19…….无限期地继续这个过程…而未被删除的号码称为“幸运数”。输入正整数N判断他是不是幸运数,输出YES或者NO。不考虑不合理的输入等特殊情况。
格式
输入格式:
输入正整数N输出格式:
输出YES或者NO
样例1
输入格式:
19输出格式:
YES
(2)参考代码
#include<stdio.h>
int main()
{ int N, del = 2;scanf("%d", &N);while (N >= del){if (N % del == 0){printf("NO");return 0;}N = N - N / del;del++;}printf("YES");return 0;
}
MT1262 约数
(1)题目
计算555555约数中最大的三位数的约数。
格式
输入格式:
无输出格式:
输出整型
样例1
输入:
无 输出:
777
(2)参考代码
#include<stdio.h>
int main()
{ int n = 555555;for (int i=999;i>=100;i--){if (n % i == 0){printf("%d\n", i);return 0;}}return 0;
}
MT1263 最大的三位约数
(1)题目
键盘任意输入一个数n(1000<=n<=1000000),编程计算并输出n的所有约数中最大的三位约数。
格式
输入格式:
输入整型输出格式:
输出整型
样例1
输入:
555555输出:
777(2)参考代码
#include<stdio.h>
int main()
{ int n;scanf("%d", &n);for (int i=999;i>=100;i--){if (n % i == 0){printf("%d\n", i);return 0;}}return 0;
}
MT1264 完数
(1)题目
如果一个整数等于其所有真因子(即除了自身以外的约数)的和,则该数字称为完数。例如,6=1+2+3,编写一个程序来查找1到1000之间的所有完数。不考虑0,负数或者其他特殊情况。
格式
输入格式:
无输出格式:
输出为整型,空格分隔
样例1
输入:
无输出:
6 28 496
(2)参考代码
#include<stdio.h>
int main()
{ int sum = 0;for (int i=1;i<=1000;i++){for (int j=1;j<i;j++){if (i % j == 0){sum += j;}}if (sum == i){printf("%d ", i);}sum = 0;}return 0;
}
MT1265 区间完数
(1)题目
如果一个整数等于其所有真因子之和,则该数字称为完数。例如,6=1+2+3,输入整数区间,输出区间(含边界)内所有的完数。不考虑0,负数或者其他特殊情况。
格式
输入格式:
输入为整型,空格分隔输出格式:
输出为整型,空格分隔
样例1
输入:
1 500输出:
6 28 496
(2)参考代码
#include<stdio.h>
int main()
{ int a, b, sum = 0;scanf("%d %d", &a, &b);for (int i=a;i<=b;i++){for (int j=1;j<i;j++){if (i % j == 0){sum += j;}}if (sum == i){printf("%d ", i);}sum = 0;}return 0;
}
MT1266 完数与因子
(1)题目
如果一个整数等于其所有真因子之和,则该数字称为完数。例如,6=1+2+3,按指定格式输出1到1000之间的所有完数他们的真因子。不考虑0,负数或者其他特殊情况。
格式
输入格式:
无输出格式:
分行输出
样例1
输入:
无输出:
6=1+2+3
28=1+2+4+7+14
496=1+2+4+8+16+31+62+124+248
(2)参考代码
#include<stdio.h>
int main()
{int sum = 0;for (int i = 1; i <= 1000; i++){for (int j = 1; j < i; j++){if (i % j == 0){sum += j;}}if (sum == i){printf("%d=", i);for (int j = 1; j < i; j++){if (i % j == 0){if (i / j == 2){printf("%d", j);}else{printf("%d+", j);}}}printf("\n");}sum = 0;}return 0;
}
MT1267 亏数
(1)题目
输入正整数N,如果N的所有因子之和小于两倍的N,该数字则称为亏数。判断N是否为亏数输出YES或者NO。
格式
输入格式:
输入正整数N输出格式:
输出YES或者NO
样例1
输入:
12输出:
NO
(2)参考代码
#include<stdio.h>
int main()
{ int N, sum = 0;scanf("%d", &N);for (int i=1;i<=N;i++){if (N % i == 0){sum += i;}}if (sum < 2 * N){printf("YES");}else{printf("NO");}return 0;
}
MT1268 因数的因数
(1)题目
输入正整数N,任务是求N的所有因数的因数之和。54的因数=1,2,3,6,9,18,27,54。
其中1的所有因数之和是1,2的所有因数之和是1+2=3,依次类推,所有因数的因数之和分别为1,3,4,12,13,39,40,120。那么54的所有因数的因数之和= 1 + 3 + 4 + 12 + 13 + 39 + 40 + 120 = 232
格式
输入格式:
输入正整数N输出格式:
输出整型
样例1
输入:
10输出:
28
(2)参考代码
#include<stdio.h>
int main()
{ int N, sum = 0;scanf("%d", &N);for (int i=1;i<=N;i++){if (N % i == 0){for (int j=1;j<=i;j++){if (i % j ==0){sum += j;}}}}printf("%d\n", sum);return 0;
}
MT1269 区间素数
(1)题目
输入整数区间,输出区间(含边界)内所有的素数。如果没有则输出空。不考虑0,负数或者其他特殊情况。
格式
输入格式:
输入为整型,空格分隔输出格式:
输出为整型,空格分隔
样例1
输入:
100 130输出:
101 103 107 109 113 127
(2)参考代码
#include<stdio.h>
int main()
{ int a, b, flag = 1;scanf("%d %d", &a, &b);for (int i=a;i<=b;i++){if (i != 1){for (int j=2;j<i;j++){if (i % j == 0){flag = 0;}}if (flag == 1){printf("%d ", i);}flag = 1;}}return 0;
}
MT1270 素数计算
(1)题目
编写一个程序来计算m到n之间的素数(含边界)。然后计算总和=第一个素数-第二个素数+第三个素数-第四个素数+第五个素数…,这些素数按降序排列。
格式
输入格式:
输入为整型,空格分隔输出格式:
输出为整型
样例1
输入:
500 800输出:
130
(2)参考代码
#include<stdio.h>
int main()
{ int a, b, flag = 1, sum = 0, num = -1;scanf("%d %d", &a, &b);for (int i=b;i>=a;i--){if (i != 1){for (int j=2;j<i;j++){if (i % j == 0){flag = 0;}}if (flag == 1){num = -num;sum = sum + i * num;}flag = 1;}}printf("%d\n", sum);return 0;
}
MT1271 三生质数
(1)题目
若三个连续的质数,相邻两个都相差2的,叫三生质数。输入正整数N,输出N以内(含N)的三生质数。没有就输出0。
格式
输入格式:
输入整型输出格式:
输出整型,空格分隔,每行一组。
样例1
输入格式:
100输出格式:
3 5 7
(2)参考代码
#include<stdio.h>
#define MAX_NUM 500
int main()
{ int N, num = 0, flag = 0;scanf("%d", &N);int Check[MAX_NUM] = {1, 1}, primes[MAX_NUM] = {0};for (int i=2;i<MAX_NUM;i++){if (Check[i] == 0){for (int j=2;j * i <MAX_NUM;j++){Check[i * j] = 1;}primes[num++] = i;}}for (int i=0;i<num-2;i++){if (primes[i] == primes[i+1]-2 && primes[i+1] == primes[i+2]-2){flag = 1;printf("%d %d %d", primes[i], primes[i+1], primes[i+2]);}}if (flag == 0){printf("0");}return 0;
}
MT1272 双素数
(1)题目
数学中,两个素数的乘积所得的自然数我们称之为半素数,也叫“双素数”,输入一个正整数,判断他是不是双素数,输出YES或者NO。注意1不是双素数。不考虑0,负数等特殊情况。
格式
输入格式:
输入整型输出格式:
输出YES或者NO
样例1
输入:
6输出:
YES
备注
输入N小于500
(2)参考代码
#include<stdio.h>
int PrimeNumber(int num)
{int flag = 1;for (int k=2;k<num;k++){if (num % k == 0){flag = 0;}}return flag;
}
int main()
{ int N, i, j;scanf("%d", &N);for (i=2;i<N;i++){if (PrimeNumber(i)){for (j=2;j<N;j++){if (PrimeNumber(j)){if (N % i == 0 && N % j == 0 && i * j == N){printf("YES");return 0;}}}}}printf("NO");return 0;
}
MT1273 N以内双素数
(1)题目
数学中,两个素数的乘积所得的自然数我们称之为半素数,也叫“双素数”,输入一个正整数,输出0到N之间(包括N)所有双素数。注意1不是双素数。不考虑0,负数等特殊情况。
格式
输入格式:
输入整型输出格式:
输出整型,空格分隔。
样例1
输入:
26输出:
4 6 9 10 14 15 21 22 25 26
(2)参考代码
#include<stdio.h>
int PrimeNumber(int num)
{int flag = 1;for (int t = 2; t < num; t++){if (num % t == 0){flag = 0;}}return flag;
}
int main()
{ int N;scanf("%d", &N);for (int i=2;i<=N;i++){for (int j=2;j<i;j++){if (PrimeNumber(j)){for (int k=2;k<i;k++){if (PrimeNumber(k)){if (i % k == 0 && i % j == 0 && k * j == i){printf("%d ", i);goto again;}}}}}again:;}return 0;
}
MT1274 都相差6
(1)题目
请编写一个简单程序,输出5个质数,使相邻的每两个质数都相差6,并把它们按由小到大的顺序排列起来。这样的可能有多组,输出最小的一组。
格式
输入格式:
无输出格式:
输出整型,空格分隔。
样例1
输入:
无输出:
5 11 17 23 29
(2)参考代码
#include<stdio.h>
int main()
{ int flag;for (int i=2;;i++){flag = 1;for (int j=i;j <= i + 24;j += 6){for (int k=2;k<j;k++){if (j % k == 0){flag = 0;break;}}if (flag == 0){break;}}if (flag == 1){for (int n=i;n <= i + 24;n += 6){printf("%d ", n);}break;}}return 0;
}
MT1275 都相差10
(1)题目
请编写一个简单程序,由小到大的顺序输出3个相差10的质数。这样的可能有多组,输出最小的一组。
格式
输入格式:
无输出格式:
输出整型,空格分隔。
样例1
输入:
无输出:
3 13 23
(2)参考代码
#include<stdio.h>
int main()
{ int flag;for (int i=2;;i++){flag = 1;for (int j=i;j <= i + 20;j += 10){for (int k=2;k<j;k++){if (j % k == 0){flag = 0;break;}}if (flag == 0){break;}}if (flag == 1){for (int n=i;n <= i + 20;n += 10){printf("%d ", n);}break;}}return 0;
}
MT1276 偶数N
(1)题目
输入偶数N(偶数N大于2),返回两个素数,其和等于偶数N。可能有几种的组合,仅输出最小值所在的组合,按从小到大输出。
格式
输入格式:
输入偶数N 输出格式:
输出整型,空格分隔。
样例1
输入:
74输出:
3 71
(2)参考代码
#include<stdio.h>
int main()
{ int N, num, flag = 1;scanf("%d", &N);for (int i=2;i<N;i++){for (int j=2;j<i;j++){if (i % j == 0){flag = 0;}}if (flag == 1){num = N - i;for (int j=2;j<num;j++){if (num % j == 0){flag = 0;}}if (flag == 1){printf("%d %d\n", i, num);return 0;}}flag = 1;}return 0;
}
MT1277 合数世纪
(1)题目
如果一个世纪中的100个年号都不是素数,这个世纪就叫做合数世纪。求第一个合数世纪。从公元0年开始算。
格式
输入格式:
无输出格式:
输出这个世纪的第一年
样例1
输入:
无输出:
1671800
(2)参考代码
#include<stdio.h>
#include<math.h>
int main()
{ int flag1, flag2;for (int i=0;;i+=100){flag2 = 1;for (int j=i;j<=i+100;j++){flag1 = 0;for (int k=2;k<sqrt(j);k++){// if (k == 0 || k == 1)// {// flag1 = 1;// break;// }if (j % k == 0){flag1 = 1;}}if (flag1 == 0){flag2 = 0;break;}}if (flag2 == 1){printf("%d", i);break;}}return 0;
}
MT1278 自然数N的立方
(1)题目
自然数n的立方等于包含n个连续奇数的序列之和。比如2的立方等于2个连续奇数3、5之和,3的立方等于3个连续奇数7、9、11之和。输入n,按下面格式输出。不考虑0,负数或者其他特殊情况。
格式
输入格式:
输入为整型输出格式:
输出为整型
样例1
输入:
5输出:
5*5*5=21+23+25+27+29=125
(2)参考代码
#include<stdio.h>
#include<math.h>
int main()
{ int n, cube_n, middle, first;scanf("%d", &n);int a[n];cube_n = pow((double)n, 3.0);if (n % 2 == 0){middle = cube_n / n;first = middle - 1 - (n - 2);a[0] = first;for (int i=1;i<n;i++){a[i] = a[i-1] + 2; }}else{middle = cube_n / n;first = middle - (n - 1);a[0] = first;for (int i=1;i<n;i++){a[i] = a[i-1] + 2;}}printf("%d*%d*%d=", n, n, n);for (int i=0;i<n;i++){if (i == n - 1){printf("%d=", a[i]);}else{printf("%d+", a[i]);}}printf("%d", cube_n);return 0;
}
MT1279 危险的粒子
(1)题目
核反应堆中每秒钟内一个c粒子可以产生3个β粒子,而一个β粒子可以产生1个α粒子和2个β粒子。若在t=0时刻反应堆中有一个α粒子,求t秒时反应堆中分别有多少个α粒子和β粒子。不考虑不合理的输入等特殊情况。
格式
输入格式:
输入整型输出格式:输入整型,空格分隔
样例1
输入格式:
6输出格式:
183 546
(2)参考代码
#include<stdio.h>
int main()
{ int t, a = 1, b = 0, temp;scanf("%d", &t);for (int i=0;i<t;i++){temp = a;a = b;b = 3 * temp + 2 * b;}printf("%d %d", a, b);return 0;
}
MT1280 后2位数
(1)题目
输入两个整数x和y,计算x的y次方的最后2位数。不考虑负数。
格式
输入格式:
输入为整型,空格分隔输出格式:
输出为整型样例1
输入:
13 12输出:
81
(2)参考代码
#include<stdio.h>
#include<math.h>
int main()
{ int x, y, num = 1;scanf("%d %d", &x, &y);for (int i=0;i<y;i++){num *= x;num %= 100;}printf("%d", num);return 0;
}
相关文章:

算法竞赛入门【码蹄集新手村600题】(MT1260-1280)C语言
算法竞赛入门【码蹄集新手村600题】(MT1260-1280)C语言 目录MT1260 袋鼠躲猫猫MT1261 留下来的才是幸运数MT1262 约数MT1263 最大的三位约数MT1264 完数MT1265 区间完数MT1266 完数与因子MT1267 亏数MT1268 因数的因数MT1269 区间素数MT1270 素数计算MT1271 三生质数…...
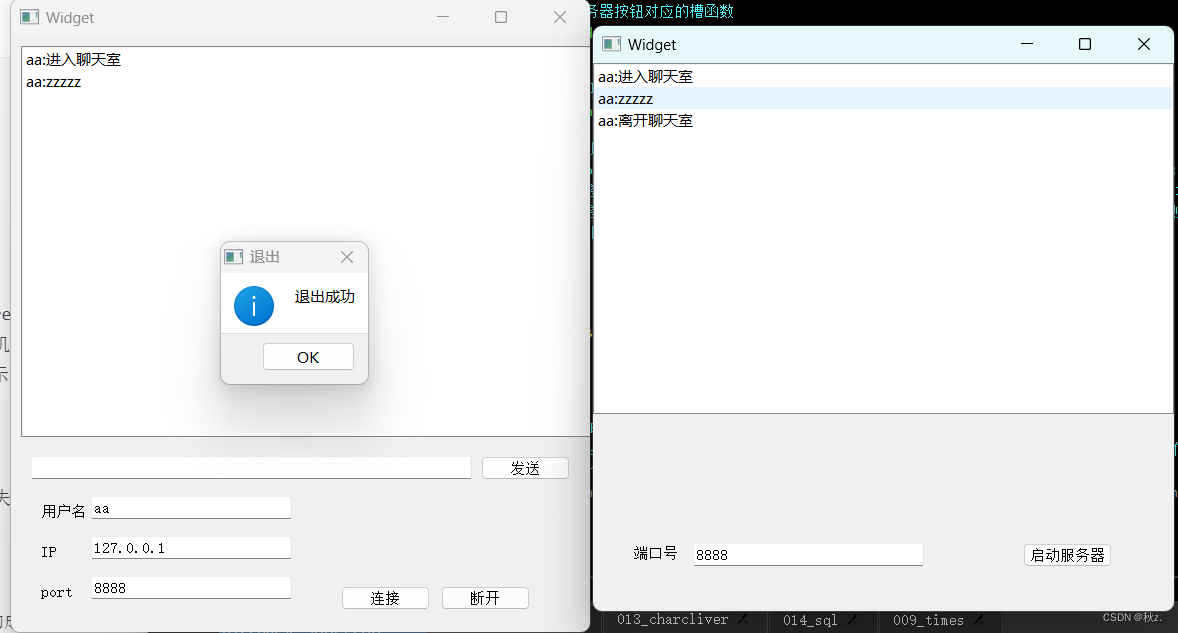
qt连接tcp通信和连接数据库
通过数据库实现学生管理系统 widget.cpp #include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);//判断数据库对象是否包含了自己使用的数据库 Studemt.dbif(!db.co…...

MySQL Oracle区别
由于SQL Server不常用,所以这里只针对MySQL数据库和Oracle数据库的区别 (1) 对事务的提交 MySQL默认是自动提交,而Oracle默认不自动提交,需要用户手动提交,需要在写commit;指令或者点击commit按钮 (2) 分页查询 MySQL是直接在SQL语…...
Figma实用插件速收藏!精选19个干货插件大公开!
Figma 如今有着大量的插件,在 UI/UX 设计领域,很多工作已经不用真的从零开始做了。用好 Figma 插件,往往能让设计工作事半功倍。不过其中的插件素质差别很大,需要仔细筛选。不过如果你选择了对的插件,合理的设置&#…...

【STM32】FSMC—扩展外部 SRAM 初步使用 1
基于野火指南者《零死角玩转 STM32F103—指南者》的学习 STM32F103系列 FSMC Flexible Static Memory Controller简介 1.详细功能参看《STM32F10x参考手册》,这边是概述 是一个外设,挂载在AHB总线下。 可以用于驱动包括 SRAM、NOR FLASH 以及 NAND FL…...
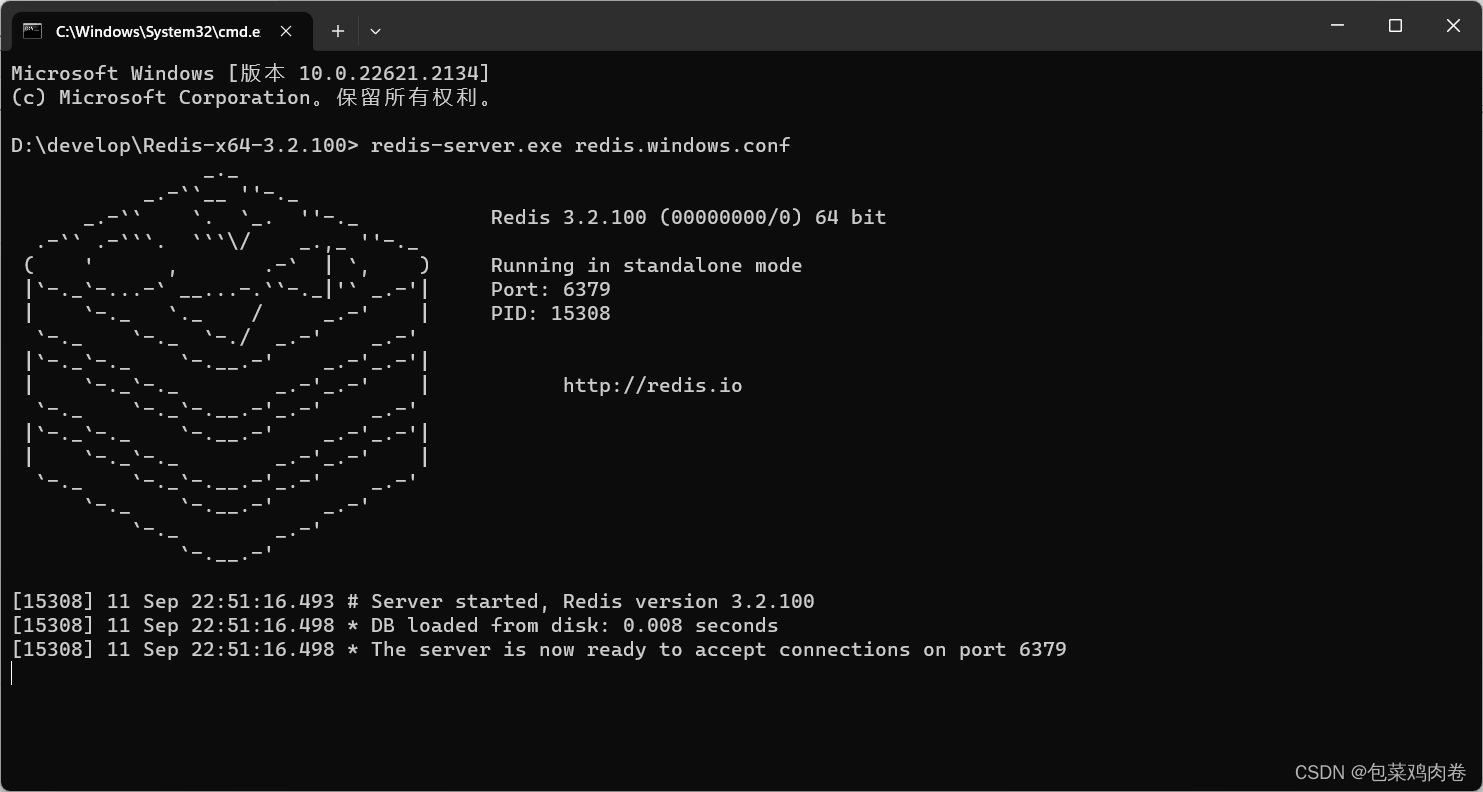
保姆级教程 --redis启动命令
1、在redis目录 打开命令 windowr 输入cmd 2、输入 redis-server.exe redis.windows.conf 启动redis命令,看是否成功 3、可能会启动失败,报28 Nov 09:30:50.919 # Creating Server TCP listening socket 127.0.0.1:6379: bind: No error 4、报错后&am…...
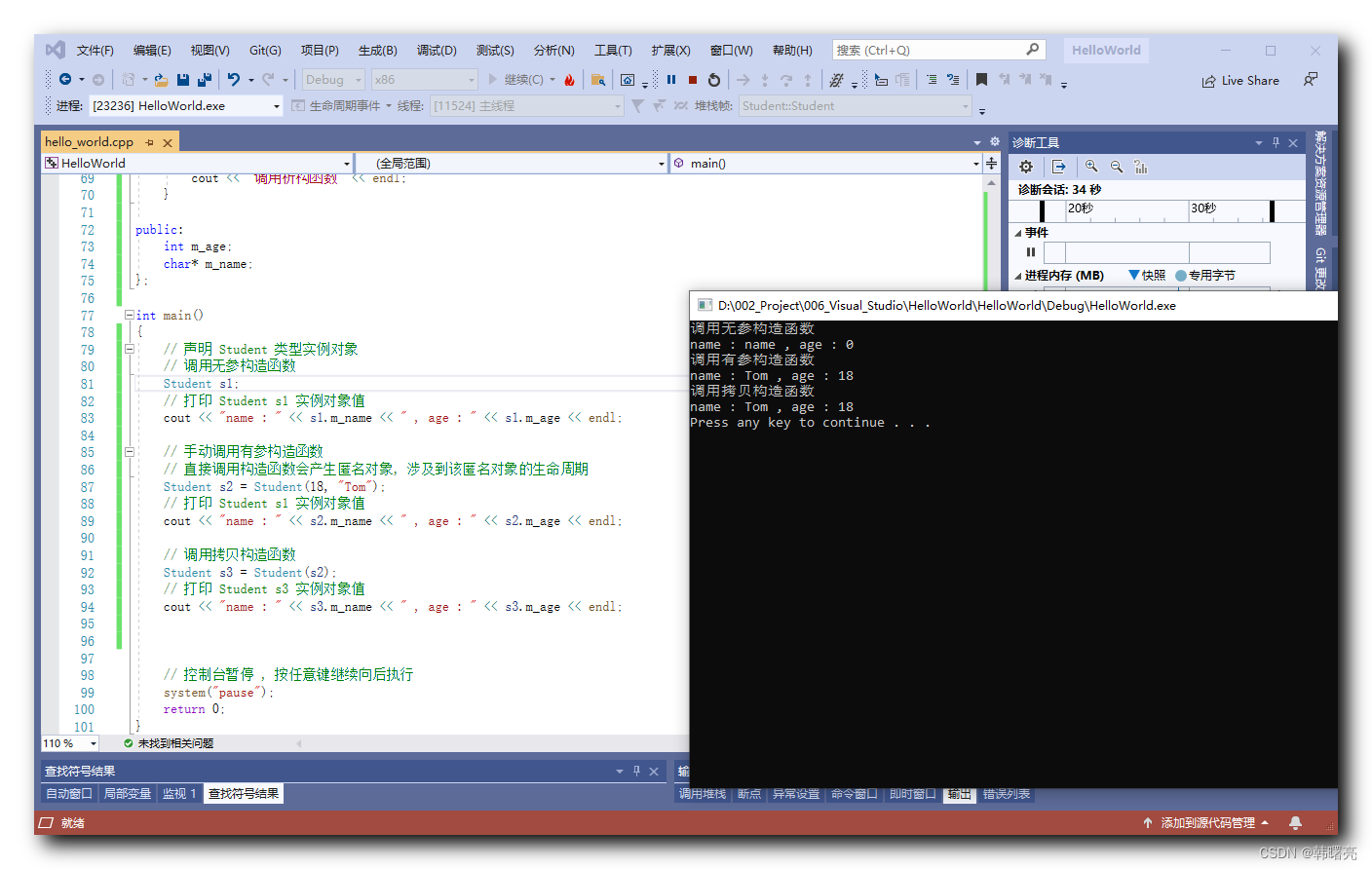
【C++】构造函数分类 ① ( 构造函数分类简介 | 无参构造函数 | 有参构造函数 | 拷贝构造函数 | 代码示例 - 三种类型构造函数定义与调用 )
文章目录 一、构造函数分类1、构造函数分类简介2、构造函数分类代码分析无参构造函数有参构造函数拷贝构造函数 二、代码示例 - 三种类型构造函数定义与调用 一、构造函数分类 1、构造函数分类简介 C 构造函数可以分为以下几类 : 无参构造函数 : 最简单也是默认的构造函数 , 函…...

胡焕庸线,我国东西地级市分布密度分界线
背景 黑河—腾冲线,又名胡焕庸线,是我国人口密度分布的东西近似分界线。今天把地级市坐标分布密度做成热力图,并与胡焕庸线一起展示时,惊奇的发现,胡焕庸线貌似也是我车东西地级市分布密度的分界线。 生成folium地图…...
或重载时应遵循的规则)
里氏替换原则在继承关系中子类对父类方法的重写(覆盖)或重载时应遵循的规则
什么是里氏替换原则:只要父类能出现的地方子类就可以出现,而且 替换为子类也不会产生任何错误或异常,使用者可能根本就不需要知道是父类还是子类。但是,反过来就不行了,有子类出现的地方,父类未必就能适应。…...

【脑机接口开源数据处理包】brainflowBrainFlow是一个库,旨在获取,解析和分析脑电图,肌电图,心电图和其他类型的数据从生物传感器。
BrainFlow是一个库,旨在获取,解析和分析脑电图,肌电图,心电图和其他类型的数据从生物传感器。 brainflow开源库官网地址 [https://brainflow.readthedocs.io/en/stable/](https://brainflow.readthedocs.io/en/stable/) 它提供了…...

#452. 序列操作
序列操作 - 题目 - Daimayuan Online Judge 问题描述: 思路:首先想的是第二次操作的y可以将前面所以操作进行抵消,只需要第二次操作的最大值即可。但是发现,对于第一个操作,它是单点修改,每修改一次对于第…...

《Python深度学习-Keras》精华笔记3:解决深度学习多分类问题
公众号:机器学习杂货店作者:Peter编辑:Peter 持续更新《Python深度学习》一书的精华内容,仅作为学习笔记分享。 本文是第三篇:介绍如何使用Keras解决Python深度学习中的多分类问题。 多分类问题和二分类问题的区别注意…...

区块链世界的大数据入门之zkMapReduce简介
1. 引言 跨链互操作性的未来将围绕多链dapp之间的动态和数据丰富的关系构建。Lagrange Labs 正在构建粘合剂,以帮助安全地扩展基于零知识证明的互操作性。 2. ZK大数据栈 Lagrange Labs 的ZK大数据栈 为一种专有的证明结构,用于在任意动态分布式计算的…...

Python流程控制语句-条件判断语句练习及应用详解
文章目录 简介条件判断语句(if语句)练习1:判断奇偶数练习2:判断闰年练习3:计算狗的年龄相当于人的年龄练习4:根据成绩奖励练习5:选择婚姻对象 小结 python 学习专栏推荐python基础知识ÿ…...
ElasticSearch高级使用【别名,重建索引,refresh操作,高亮查询,查询建议】)
(十)ElasticSearch高级使用【别名,重建索引,refresh操作,高亮查询,查询建议】
1.别名使用 1)别名作用 在开发中,随着业务需求的迭代,较⽼的业务逻辑就要⾯临更新甚⾄是重构,⽽对于es来说,为了 适应新的业务逻辑,可能就要对原有的索引做⼀些修改,⽐如对某些字段做调整&…...

基于小波神经网络的中药材价格预测,基于ANN的小波神经网络中药材价格预测
目标 背影 BP神经网络的原理 BP神经网络的定义 BP神经网络的基本结构 BP神经网络的神经元 BP神经网络的激活函数, BP神经网络的传递函数 小波神经网络(以小波基为传递函数的BP神经网络) 代码链接:基于小波神经网络的中药材价格预测,ANN小波神经网络中药材价格预测资源-CS…...

thinkPhp5返回某些指定字段
//去除掉密码$db new UserModel();$result $db->field(password,true)->where("username{$params[username]} AND password{$params[password]}")->find(); 或者指定要的字段的数组 $db new UserModel();$result $db->field([username,create_time…...

基于docker环境的tomcat开启远程调试
背景: Tomcat部署在docker环境中,使用rancher来进行管理,需要对其进行远程调试。 操作步骤: 1.将容器中的catalina.sh映射出来,便于对其修改,添加远程调试相关参数。 注意:/data/produce2201…...
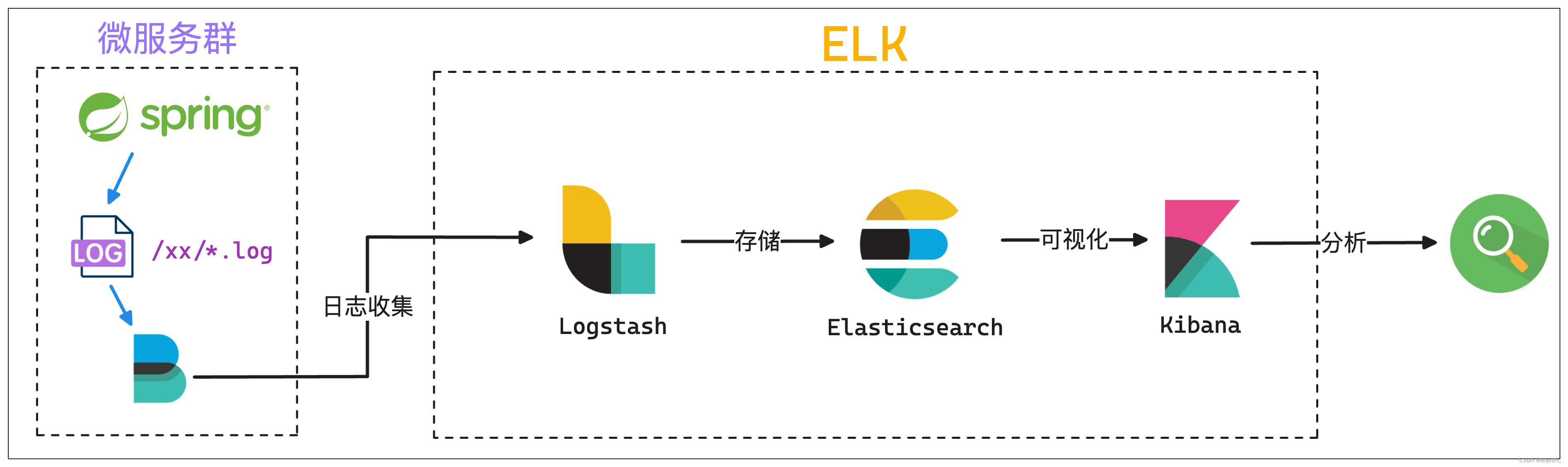
ELK日志框架图总结
ELK日志框架图总结 本文目录 ELK日志框架图总结Elastic Stack介绍模式分层图beatselasticsearchkibana模式logstashelasticsearchkibana模式beatslogstashelasticsearchkibana模式beats缓存/消息队列logstashelasticsearchkibana模式elkspringboot Elastic Stack介绍 官网&…...

go 每天定时任务 --chatGPT
问:clearLog(hour,cmds),定时执行shell 命令,hour 为每天的几点,cmds 为linux命令数组字符串(如 1,{"ls","cd"}) gpt: 要编写一个 Go 函数 clearLog,该函数可…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
