数据结构-堆的实现及应用(堆排序和TOP-K问题)
数据结构-堆的实现及应用[堆排序和TOP-K问题]
- 一.堆的基本知识点
- 1.知识点
- 二.堆的实现
- 1.堆的结构
- 2.向上调整算法与堆的插入
- 2.向下调整算法与堆的删除
- 三.整体代码
- 四.利用回调函数避免对向上和向下调整算法的修改
- 1.向上调整算法的修改
- 2.向下调整算法的修改
- 3.插入元素和删除元素函数的修改
- 五.建堆
- 1.自顶向下的建堆方式(利用向上调整算法)
- 2.自底向上的建堆方式(利用向下调整算法)
- 3.两种方法建堆的时间复杂度
- 1.向下调整算法建堆的时间复杂度
- 2.向上调整算法建堆的时间复杂度
- 六.堆排序
- 1.算法思想
- 2.代码实现
- 3.时间复杂度
- 4.稳定性
- 七.TOP-K问题
- 八.一道与TOP-K相关的leetcode题目
- 九.测试TOP-K对于海量数据的处理
- 十.总结
一.堆的基本知识点
1.知识点
1.堆的知识点:
堆的知识点
堆的逻辑结构是一颗完全二叉树
堆的物理结构是一个数组
也就是说,给我们是一个数组,可是我们要把它想象成一个完全二叉树来做
通过下标父子结点关系
leftchild = parent * 2 + 1;
rightchild = parent * 2 + 2;
parent = (child - 1) / 2;(child可以是左孩子,也可以是右孩子)
下面我们通过一张图片来更加深刻地理解堆
堆的两个特性1.结构性:用数组表示的完全二叉树
2.有序性:任意节点的关键字是其子树所有结点的最大值
3.堆的两种分类
最大堆(MaxHeap):也称为大顶堆(最大值)
最小堆(MinHeap):也称为小顶堆(最小值)
3.大堆:要求树中所有的父亲都大于等于孩子
小堆:要求所有的父亲都小于等于孩子
堆只有两种:大堆,小堆,其余的都不是堆,注意有些选择题常考堆的判别
大堆:堆顶数据是最大的
小堆:堆顶数据是最小的
二.堆的实现
1.堆的结构
上面我们说过,堆的物理结构是一个数组,逻辑结构是一个完全二叉树,所以堆的实际结构类似于顺序表,只不过我们的处理方式类似于二叉树
那么我们就可以用顺序表那样的结构来表示堆了
于是我们可以写出这样的代码
typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
//堆的初始化
void HeapInit(HP* php);
//堆的销毁
void HeapDestroy(HP* php);
//堆的打印
void HeapPrint(HP* php);
//取堆顶数据
HPDataType HeapTop(HP* php);
//判断是否为空
bool HeapEmpty(HP* php);
//返回堆的元素大小
int HeapSize(HP* php);
void HeapInit(HP* php)
{assert(php);//这里我们将容量初始化为0,当然,初始化为别的一些数值也可以,这里没有强制要求php->a = NULL;php->size = php->capacity = 0;
}void HeapDestroy(HP* php)
{assert(php);free(php->a);php->capacity = php->size = 0;php->a = NULL;
}void HeapPrint(HP* php)
{int i = 0;for (i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}int HeapSize(HP* php)
{assert(php);return php->size;
}
剩下的一些常见的接口:
//堆的插入
void HeapPush(HP* php, HPDataType x);
//堆的删除
void HeapPop(HP* php);
在这里,我们要先说明一下:
1.在堆中插入一个数据后,我们不能改变堆的特性,
即:原来是小堆,插入数据后还是小堆
原来是大堆,插入数据后还是大堆2.我们的删除操作所要删除的值是堆顶元素.
即数组的第一个元素,
删除操作依然不能改变堆的特性
要想实现堆的插入
首先我们需要先学习一个算法:向上调整算法
2.向上调整算法与堆的插入
假设我们现在有一个小堆(所有的父亲都小于他们所对应的孩子)
我们要插入一个元素

向上调整算法整体思路:
child不断向上跟父亲比,如果比父亲小,跟父亲交换,向上迭代
当该节点调整到父亲小于该节点时,或者该节点调整到数组的首元素位置时调整结束
所以我们可以写出这样的代码
//向上调整算法
//[0,child]区间内向上调整
void AdjustUp(HPDataType* a,int child)
{int parent = (child - 1) / 2;//终止条件:孩子等于0,大于0就继续调整//不要拿父亲作为条件,父亲和孩子都等于0的时候,parent = (0-1)/2还是0,死循环了//while(parent>=0)while (child > 0){//建小堆if(a[child]<a[parent])//建大堆if(a[child]>a[parent])if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
其中,向上调整算法的时间复杂度为O(log2(N)),
最多调整高度次,因为是完全二叉树,所以高度约等于O(log2(N))
实现了向上调整算法之后,我们就可以完成插入了
void HeapPush(HP* php, HPDataType x)
{assert(php);//扩容if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;//进行扩容HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (NULL == tmp){perror("malloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}//插入php->a[php->size] = x;php->size++;//向上调整AdjustUp(php->a, php->size - 1);
}
2.向下调整算法与堆的删除
假设我们现在有一个小堆

向下调整算法整体思路:
前提:根节点的左子树和右子树都是小堆
child为左右孩子中较小者
如果父亲大于child,交换父亲和child,父亲和孩子向上迭代
于是我们可以写出这样的代码
//向下调整算法(小堆)
//[root,n)区间内向下调整
void AdjustDown(HPDataType* a, int root,int n)
{int parent = root;int child = 2 * parent + 1;while (child < n){//建小堆:if(...&& a[child]>a[child+1])//建大堆:if(...&& a[child]<a[child+1])if (child + 1 < n && a[child] > a[child + 1]){child++;}//建小堆:if(a[parent]>a[child])//建大堆:if(a[parent]<a[child])if (a[parent] > a[child]){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else{break;}}
}
实现了向下调整算法的代码后,我们可以写出删除的代码
其中,向下调整算法的时间复杂度也为O(log2(N)),
最多调整高度次,因为是完全二叉树,所以高度约等于O(log2(N))
//删除堆顶元素
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&(php->a[0]), &(php->a[php->size - 1]));php->size--;AdjustDown(php->a, 0, php->size);
}
三.整体代码
Heap.h
#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
//初始化堆
void HeapInit(HP* php);
//销毁堆
void HeapDestory(HP* php);
//打印堆
void HeapPrint(HP* php);
//插入X继续保持堆形态
void HeapPush(HP* php, HPDataType x);
//删除堆顶元素
void HeapPop(HP* php);
//判断是否为空
bool HeapEmpty(HP* php);
//返回堆顶元素
HPDataType HeapTop(HP* php);
//返回堆的元素大小
int HeapSize(HP* php);
Heap.c
#include "Heap.h"
//初始化堆
void HeapInit(HP* php)
{php->a = NULL;php->capacity = php->size = 0;
}
//销毁堆
void HeapDestory(HP* php)
{free(php);php->capacity = php->size = 0;
}
//打印堆
void HeapPrint(HP* php)
{int i = 0;for (i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}void Swap(HPDataType* h1, HPDataType* h2)
{HPDataType tmp = *h1;*h1 = *h2;*h2 = tmp;
}//向上调整算法
//区间范围:[0,child]
void AdjustUp(HPDataType* a,int child)
{int parent = (child - 1) / 2;//终止条件:孩子等于0,大于0就继续调整//不要拿父亲作为条件,父亲和孩子都等于0的时候,parent = (0-1)/2还是0,死循环了//while(parent>=0)while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
//插入X继续保持堆形态(小堆:父亲小于孩子)void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;//进行扩容HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (NULL == tmp){perror("malloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}//向下调整算法(小堆)
//区间范围:[root,n)
void AdjustDown(HPDataType* a, int root,int n)
{int parent = root;int child = 2 * parent + 1;while (child < n){if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[parent] > a[child]){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else{break;}}
}//删除堆顶元素
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&(php->a[0]), &(php->a[php->size - 1]));php->size--;AdjustDown(php->a, 0, php->size);
}
//判断是否为空
bool HeapEmpty(HP* php)
{return php->size == 0;
}
//返回堆顶元素HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}//返回堆的元素大小
int HeapSize(HP* php)
{assert(php);return php->size;
}四.利用回调函数避免对向上和向下调整算法的修改
从上面的讲解中,对于向上调整算法和向下调整算法来说,如果想要实现从小堆到大堆的转换,还需要改一下代码,(尽管只需要改一下比较符号即可),
但是那样的话我们就需要再去实现针对于建大堆的向上调整算法和向下调整算法,
而且还需要根据不同需要去调用不同函数,过于麻烦
所以有什么方法可以避免这种修改吗?
在C语言中,我们可以利用回调函数来完成,对于回调函数来说,大家可以看我的这篇博客
征服C语言指针系列(3)
里面有详细的讲解
1.向上调整算法的修改
void AdjustUp(HPDataType* a, int child, int(*cmp_up)(HPDataType* p1, HPDataType* p2))
{int parent = (child - 1) / 2;while (child > 0){//小堆:if(a[parent]>a[child])//也就是说cmp_up(...,...)这个函数返回值为正数,则建的是小堆//否则,建的是大堆if (cmp_up(&a[parent], &a[child]) > 0){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
2.向下调整算法的修改
void AdjustDown(HPDataType* a, int root,int n, int(*cmp_down)(HPDataType* p1, HPDataType* p2))
{int parent = root;int child = 2 * parent + 1;while (child < n){//小堆:if(a[child]>a[child+1])//也就是说cmp_down(...,...)这个函数返回值为正数,则建的是小堆//否则,建的是大堆if (child + 1 < n && cmp_down(&a[child], &a[child + 1]) > 0){child++;}//小堆:if(a[parent]>a[child])//也就是说cmp_down(...,...)这个函数返回值为正数,则建的是小堆//否则,建的是大堆if (cmp_down(&a[parent], &a[child]) > 0){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else{break;}}
}
函数调用者自行实现两个函数
int cmp_down(HPDataType* p1, HPDataType* p2);int cmp_up(const HPDataType* p1, const HPDataType* p2);
//使用函数指针来做一个回调函数
cmp_up:向上调整
cmp_down:向下调整
//建小堆(父亲小于孩子)
int cmp_up(const HPDataType* p1, const HPDataType* p2)
{return *p1 - *p2;
}//建大堆
int cmp_up(const HPDataType* p1, const HPDataType* p2)
{return *p2 - *p1;
}//建小堆:父亲小于孩子int cmp_down(HPDataType* p1, HPDataType* p2)
{return *p1 - *p2;
}//建大堆
int cmp_down(HPDataType* p1, HPDataType* p2)
{return *p2 - *p1;
}
3.插入元素和删除元素函数的修改
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->capacity == php->size){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1, cmp_up);
}
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&(php->a[0]), &(php->a[php->size - 1]));php->size--;AdjustDown(php->a, 0, php->size, cmp_down);
}
经过了上面的修改,我们就可以在不改变代码的情况下,实现大堆或者小堆了
五.建堆
上面的代码可以让我们从无到有建立堆
但是如果我们要把一个数组改造成堆,而且不能浪费其他空间,只能在原数组上改造,那该怎么办呢?
这里我们需要建堆
这里以建小堆为例
1.自顶向下的建堆方式(利用向上调整算法)
根据上文可知进行向上调整算法后,数组中[0,child]区间就变为小堆了,所以我们可以用一个for循环来扩展这个区间让这个区间从[0,1]一直扩到[0,n-1]
于是我们可以写出如下代码
for (int i = 1; i < n; i++){AdjustUp(arr, i, cmp_up);}
下面给大家画张图看一看:

2.自底向上的建堆方式(利用向下调整算法)
既然向上调整算法可以建堆,那么向下调整算法呢?
答案是:也可以建堆
我们可以从最后一个非叶子节点往上建堆,先让下面变成小堆,再让上面变成小堆
那么我们该如何求出最后一个非叶子节点呢?
根据堆的特性,我们得出过如下结论:
parent=(child-1)/2;
parent自然是非叶子节点,那么我们只需要求出最后一个parent不就行了吗?
我们又知道最后一个child的下标一定是n-1
所以得出最后一个parent的下标是(n-1-1)/2;
根据上文我们得出向下调整算法可以使得
数组中区间[root,n)范围内变为小堆
那么我们就可以逐步扩大这个范围,让这个范围从[(n-1-1)/2,n)一直扩大到[0,n)
所以我们可以写出如下代码
for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, i, n, cmp_down);}
下面给大家画张图看一看:

3.两种方法建堆的时间复杂度
//向下调整算法for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, i, n, cmp_down);}
//向上调整算法for (int i = 1; i < n; i++){AdjustUp(arr, i, cmp_up);}
可能大家看到这两个代码后的反应是:
因为向上和向下调整算法的时间复杂度都是log(2)N
所以这两种建堆的时间复杂度不都是O(Nlog2(N))吗?
答案是:并不是这样,
向下调整算法建堆的时间复杂度:O(N)
向上调整算法建堆的时间复杂度:O(Nlog(2)N)
下面我们来用数学公式证明一下(这里需要用到错位相减法)
1.向下调整算法建堆的时间复杂度

2.向上调整算法建堆的时间复杂度

前面已经介绍了如何把一个普通的数组改造成堆
那么接下来我们来看堆的两大重要应用:
堆排序和TOP-K问题
六.堆排序
1.算法思想
1.那么排升序我们要建什么堆呢?
答案是:大堆,这个答案确实挺出人意料的,但是为什么呢?
下面我们来详细解释一下这个原因
1.建小堆为什么不可以(不建议):
2.建大堆为什么可以(建议):
因为:
堆排序是属于选择排序的一种.
如果是建小堆,最小数在堆顶,已经被选出来了,
那么在剩下的数中再去选数,但是剩下的树结构都乱了,需要重新建堆才能选出下一个数,
建堆的时间复杂度是O(N),我们在讲解堆排序的最后会给大家证明这个建堆的时间复杂度.
那么这样不是不可以,但是堆排序就没有效率优势了并且建堆选数还不如直接遍历选数
其次,如何选次小的数呢?
第二个数去做根了,剩下的树关系全乱了,再重新建堆,
建堆的时间复杂度:O(N),而建堆选数排序,时间复杂度:O(N^2)
并且建堆选数还不如直接遍历选数
下面我给大家画图来演示一下:

2.建大堆:
步骤:
1.第一个和最后一个交换,然后把交换后的那个较大的数(即位于数组末尾的那个数)不看做堆里面
2.前n-1和数进行向下调整算法,选出次大的数放到根节点,再跟倒数第二个位置交换
2.代码实现
代码如下:
void HeapSort(int* a,int n)
{int i = 0;//这里用向下调整算法来建堆,因为时间复杂度只有O(N)for (i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustUp(a, end, 0);--end;}
}
下面给大家画图演示一下,能帮助大家有更好的理解





3.时间复杂度
void HeapSort(int* a,int n)
{int i = 0;for (i = (n - 1 - 1) / 2; i >= 0; i--){AdjustUp(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustUp(a, end, 0);--end;}
}
向下调整算法最坏的情况:进行高度次,即log(2)N次,所以while循环最坏进行了(n-1)log(2)N次,而for循环的建堆的时间复杂度为O(N)
所以整体的时间复杂度为O(Nlog(2)N)
整个效率相对来说是很高的
4.稳定性
堆排序是不稳定的
因为建堆的时候有可能发生以下的类似情况
七.TOP-K问题
可能很多小伙伴有这么一个疑问:什么是TOP-K问题啊?
TOP-K问题:
就是求数据集合中前K个最大或者最小的元素,一般情况下数据量都比较大
比如:
全国企业500强,专业前10名,全国高考前100名等等…
那么我们如何利用堆来解决TOP-K问题呢?
假设有10亿个数据,内存存不下,数据在文件中
找出最大的前K个, K==1001.读取文件的前100个数据,在内存数组中建立一个小堆
2.再依次读取剩下的数据,跟堆顶数据比较,大于堆顶,就替换它进堆,向下调整
3.所有数据读取完毕,堆里面的数据就是最大的前100个那么我们要建小堆还是大堆呢?
答案是:找最大的前K个就建小堆
反之,建大堆
为什么不建议建大堆:大堆只能找出最大的一个数,
而且最大的数会挡在根节点的位置,后面的数完全无法进堆,那就完蛋了小堆的优势
而小堆的话,只有第K个大的数才会挡在根节点的位置,而更大的数会往堆的下面跑
时间复杂度O(N*logK),而且K相对于N来说可以忽略不计,所以可以认为是O(N)
时间复杂度:O(K),K:堆的大小,而K相对于N来说可以忽略不计,所以可以认为是O(1)
下面我们结合一道leetcode题目来实现一下这个代码
八.一道与TOP-K相关的leetcode题目
最小K个数
void Swap(int*p1,int*p2)
{int tmp =*p1;*p1 = *p2;*p2 = tmp;
}
//前k个数建大堆
//向下调整算法void AdjustDown(int*a,int n,int parent){int minchild = parent*2+1;while(minchild<n){if(minchild+1<n&&a[minchild+1]>a[minchild]){minchild++;}if(a[minchild]>a[parent]){Swap(&a[minchild],&a[parent]);parent = minchild;minchild = parent*2+1;}else{break;}}}
int* smallestK(int* arr, int arrSize, int k, int* returnSize){if(k==0){*returnSize=0;return NULL;}int* ret=(int*)malloc(sizeof(int)*k);for(int i=0;i<k;i++){ret[i]=arr[i];}//前k个数建大堆for(int i=(k-1-1)/2;i>=0;i--){AdjustDown(ret,k,i);}for(int i=k;i<arrSize;i++){if(ret[0]>arr[i]){ret[0]=arr[i];AdjustDown(ret,k,0);}}*returnSize=k;return ret;
}

九.测试TOP-K对于海量数据的处理
下面我们来测试一下TOP-K对于大数据的处理功能
//创建一个文件,并且随机生成一些数字
void CreateDataFile(const char* filename, int N)
{FILE* Fin = fopen(filename, "w");if (Fin == NULL){perror("fopen fail");exit(-1);}srand(time(0));for (int i = 0; i < N; i++){fprintf(Fin, "%d ", rand() % 10000);}
}
void PrintTopK(const char* filename, int k)
{assert(filename);FILE* fout = fopen(filename, "r");if (fout == NULL){perror("fopen fail");return;}int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL){perror("malloc fail");return;}//读前k个数for (int i = 0; i < k; i++){//空格和换行默认是多个值之间的间隔fscanf(fout, "%d", &minheap[i]);}//建k个数的堆for (int j = (k - 1 - 1) / 2; j >= 0; j--){AdjustDown(minheap, j, k, cmp_down);}//读取后N-K个int x = 0;while(fscanf(fout,"%d",&x)!=EOF){if (x > minheap[0]){minheap[0] = x;AdjustDown(minheap, 0, k, cmp_down);}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}printf("\n");free(minheap);fclose(fout);
}
int main()
{//CreateDataFile("data.txt", 1000000);//找前10个最大的数PrintTopK("data.txt", 10);return 0;
}

我们已经提前修改了文件当中的值,
现在文件当中的最大的前10个值是1000000到1000009
运行后的结果:

可见堆针对于TOP-K的强大之处
十.总结
本文介绍了
1.堆的知识点
2.用C语言实现了堆
3.并且用函数指针实现了回调函数对向上和向下调整算法的代码进行了优化
4.实现了建堆
5.用数学公式推导出了两种建堆方法的时间复杂度
6.实现了堆排序
7.分析了堆排序的时间复杂度和稳定性
8.介绍了TOP-K的代码实现并解决了一道leetcode题目
9.测试了TOP-K对于大数据的处理功能
以上就是<<数据结构-堆的实现及应用>>的讲解,希望能对大家有所帮助,谢谢大家!
相关文章:

数据结构-堆的实现及应用(堆排序和TOP-K问题)
数据结构-堆的实现及应用[堆排序和TOP-K问题] 一.堆的基本知识点1.知识点 二.堆的实现1.堆的结构2.向上调整算法与堆的插入2.向下调整算法与堆的删除 三.整体代码四.利用回调函数避免对向上和向下调整算法的修改1.向上调整算法的修改2.向下调整算法的修改3.插入元素和删除元素函…...

Spring 条件注解没生效?咋回事
条件注解相信各位小伙伴都用过,Spring 中的多环境配置 profile 底层就是通过条件注解来实现的,松哥在之前的 Spring 视频中也有和大家详细介绍过条件注解的使用,感兴趣的小伙伴戳这里:Spring源码应该怎么学?。 从 Spr…...

96. 不同的二叉搜索树
class Solution { public:int numTrees(int n) {if (n0) {return 1;}vector<int> dp(n1, 0);dp[0] 1;dp[1] 0;for (int i 1; i < n; i) {for (int j 0; j < i; j) {dp[i] dp[j] * dp[i - 1 - j];}}return dp[n];} };...

Android Jetpack 中Hilt的使用
Hilt 是 Android 的依赖项注入库,可减少在项目中执行手动依赖项注入的样板代码。执行 手动依赖项注入 要求您手动构造每个类及其依赖项,并借助容器重复使用和管理依赖项。 Hilt 通过为项目中的每个 Android 类提供容器并自动管理其生命周期,…...

批量采集的时间管理与优化
在进行大规模数据采集时,如何合理安排和管理爬取任务的时间成为了每个专业程序员需要面对的挑战。本文将分享一些关于批量采集中时间管理和优化方面的实用技巧,帮助你提升爬虫工作效率。 1. 制定明确目标并设置合适频率 首先要明确自己所需获取数据的范…...

uniApp监听左右滑动事件
监听左右滑动事件的步骤 1. 添加需要监听滑动事件的元素 在你的页面中,添加需要监听滑动事件的元素。这可以是一个 view、swiper 或其他组件,取决于你的需求。例如: <template><view class"body" touchstart"touc…...
十八、MySQL添加外键?
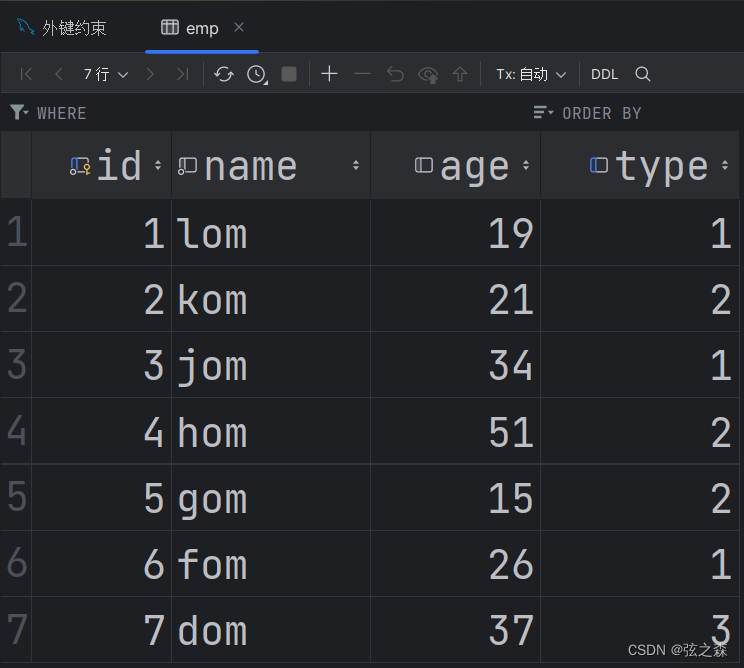
1、外键 外键是用来让两张表的数据之间建立联系,从而保证数据的一致性和完整性。 注意,父表被关联的字段类型,必须和子表被关联的字段类型一致。 2、实际操作 (1)初始化两张表格: 子表: 父…...
图像文件的操作MATLAB基础函数使用
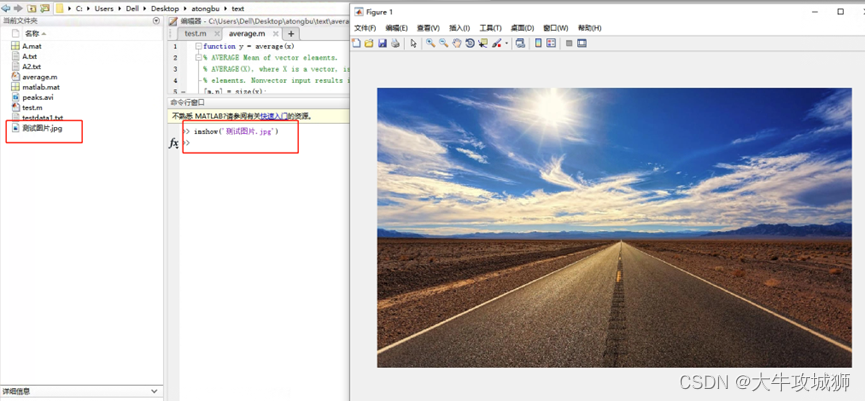
简介 MATLAB中的图像处理工具箱体统了一套全方位的标准算法和图形工具,用于进行图像处理、分析、可视化和算法开发。这里仅仅对常用的基础函数做个使用介绍。 查询图像文件的信息 使用如下函数 imfinfo(filename,fmt) 函数imfinfo返回一个结构体的infoÿ…...
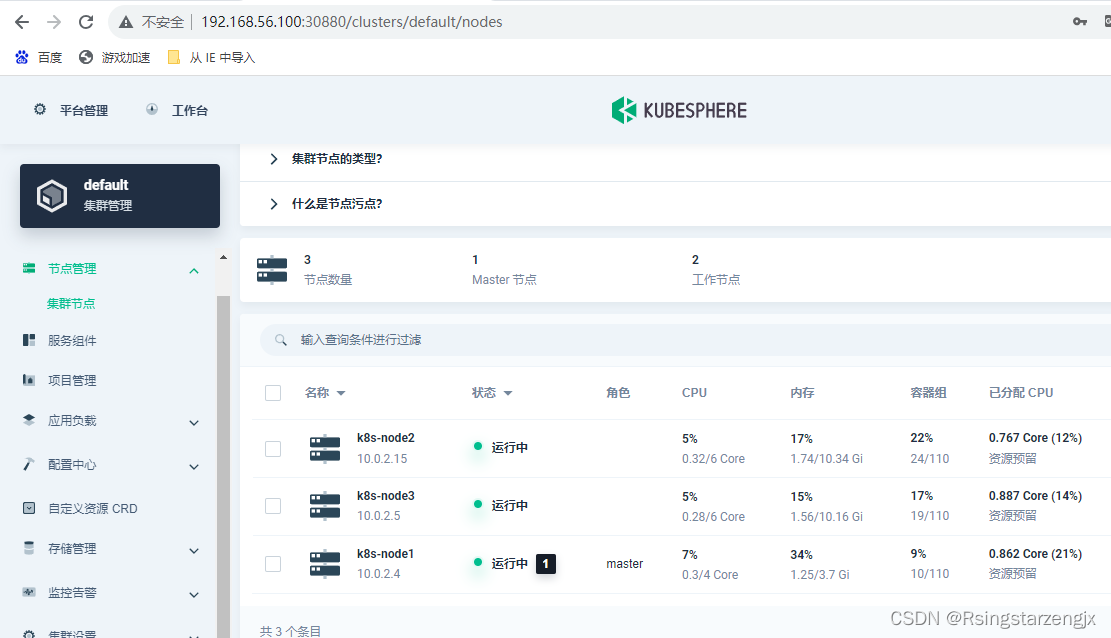
【k8s】Kubernetes版本v1.17.3 kubesphere 3.1.1 默认用户登录失败
1.发帖: Kubernetes版本v1.17.3 kubesphere 3.11 默认用户登录失败 - KubeSphere 开发者社区 2. 问题日志: 2.1问题排查方法 : 用户无法登录 http://192.168.56.100:30880/ 2.2查看用户状态 kubectl get users [rootk8s-node1 ~]# k…...

Mysql加密功能
Mysql加密功能 InnoDB加密功能查询条件问题开启整个数据库加密 InnoDB加密功能 InnoDB是MySQL数据库引擎的一种,它提供了加密存储的功能。具体来说,InnoDB引擎支持以下两种方式的加密存储: 表级加密:InnoDB支持表级加密ÿ…...

redis-win10安装和解决清缓存报错“Error: Protocol error, got “H“ as reply type byte”
win10安装 https://github.com/microsoftarchive/redis/releases 下载最新的zip,解压,把路径加到Path里,每次直接在cmd里 redis-server.exeError: Protocol error, got “H” as reply type byte 这个报错是因为我端口写错了。。无语 D:…...

【视觉检测】电源线圈上的导线弯直与否视觉检测系统软硬件方案
检测内容 线圈上的导线弯直与否检测系统。 检测要求 检测线圈上的导线有无弯曲,弯曲度由客户自己设定。检测速度5K/8H625PCS/H。 视觉可行性分析 对样品进行了光学实验,并进行图像处理,原则上可以使用机器视觉进行测试测量…...
Java elasticsearch scroll模板实现
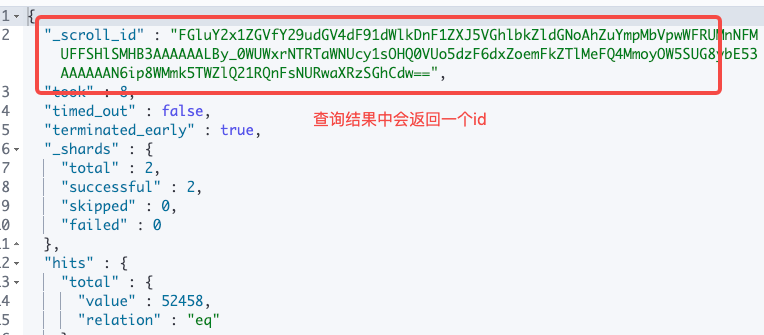
一、scroll说明和使用场景 scroll的使用场景:大数据量的检索和操作 scroll顾名思义,就是游标的意思,核心的应用场景就是遍历 elasticsearch中的数据; 通常我们遍历数据采用的是分页,elastcisearch还支持from size的…...
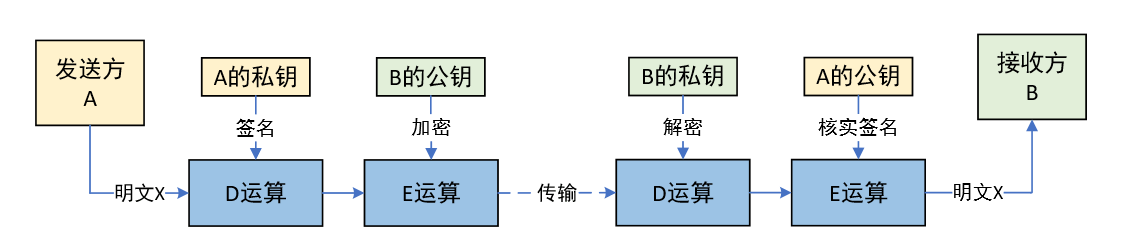
嵌入式基础知识-信息安全与加密
本篇来介绍计算机领域的信息安全以及加密相关基础知识,这些在嵌入式软件开发中也同样会用到。 1 信息安全 1.1 信息安全的基本要素 保密性:确保信息不被泄露给未授权的实体。包括最小授权原则、防暴露、信息加密、物理加密。完整性:保证数…...
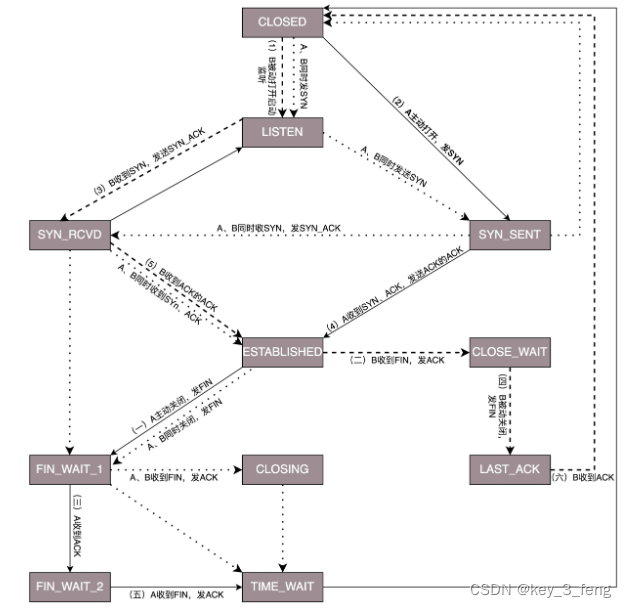
TCP的三次握手与四次挥手
首先,源端口号和目标端口号是不可少的,这一点和 UDP 是一样的。如果没有这两个端口号。数据就不知道应该发给哪个应用。 接下来是包的序号。为什么要给包编号呢?当然是为了解决乱序的问题。不编好号怎么确认哪个应该先来,哪个应该…...

【Face Swapping综述】Quick Overview of Face Swap Deep Fakes
【Face Swapping综述】Quick Overview of Face Swap Deep Fakes 0、前言Abstract1. Introduction2. Face Swapping Process2.1. Preprocessing2.2. Identity Extraction2.3. Attributes Extractor2.4. Generator2.5. Postprocessing2.6. Evaluation Methods3. Challenges4. Con…...
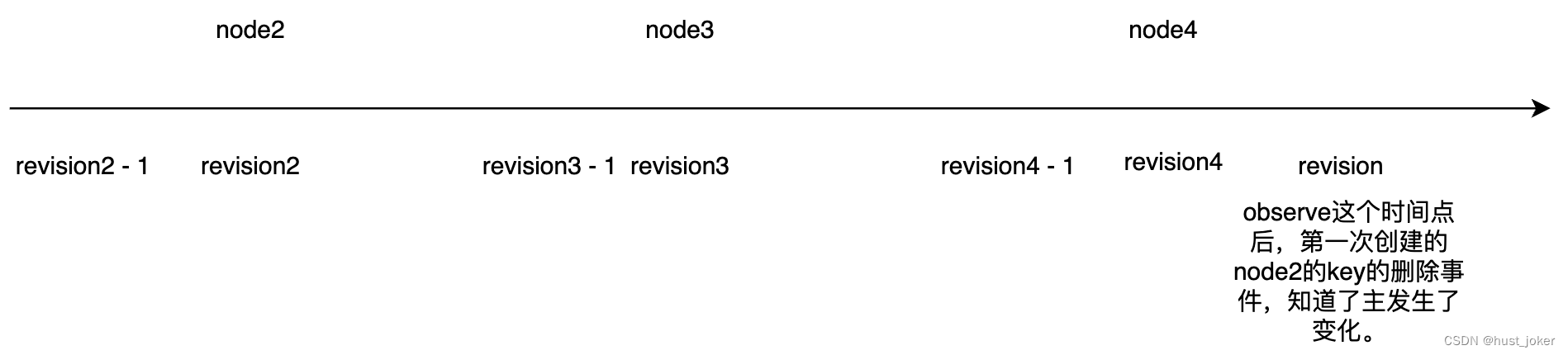
etcd选举源码分析和例子
本文主要介绍etcd在分布式多节点服务中如何实现选主。 1、基础知识 在开始之前,先介绍etcd中 Version, Revision, ModRevision, CreateRevision 几个基本概念。 1、version 作用域为key,表示某个key的版本,每个key刚创建的version为1&#…...
Android 网络配置
ip tables 和 ip route 是两个不同的工具,它们在不同的阶段执行不同的功能。ip route 是用来管理和控制路由表的,它决定了数据包应该从哪个网卡或网关发送出去。ip tables 是用来配置、管理和控制网络数据包的过滤、转发和转换的,它根据用户定…...
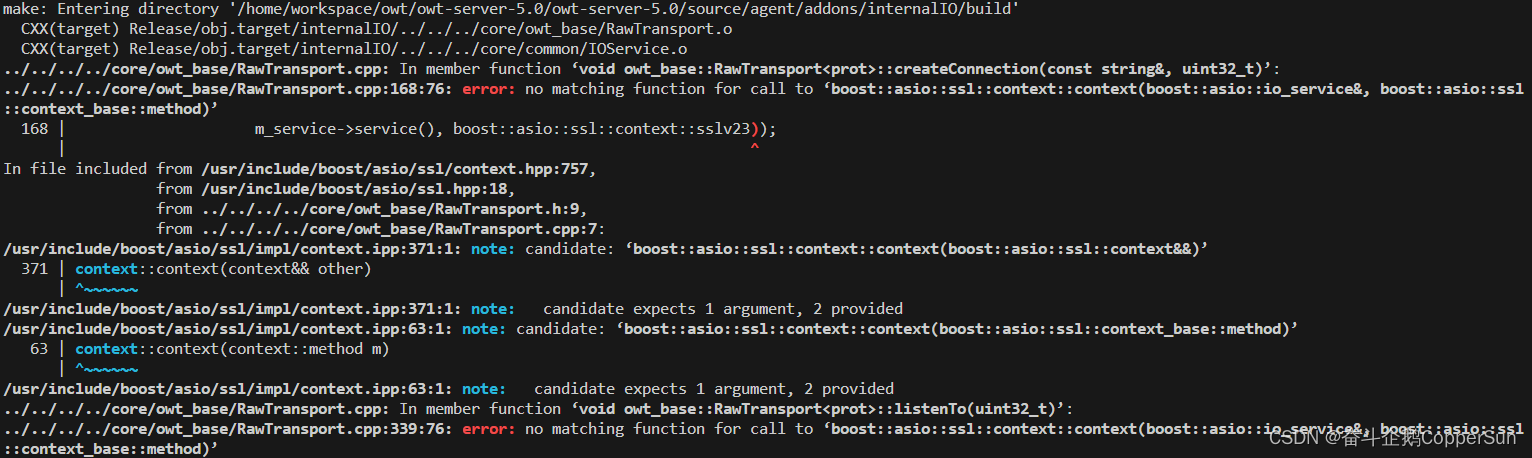
【网络通信 -- WebRTC】Open WebRTC Toolkit 环境搭建指南
【网络通信 -- WebRTC】Open WebRTC Toolkit -- OWT-Server 编译安装指南 【1】OWT Server 与 Web Demo 视频会议环境搭建 【1.1】编译 OWT Server 安装依赖 ./scripts/installDepsUnattended.sh编译 scripts/build.js -t all --check 注意若不支持硬件加速则采用如下命令 s…...
文件上传漏洞(CVE-2022-30887)
简介 多语言药房管理系统(MPMS)是用PHP和MySQL开发的,该软件的主要目的是在药房和客户之间提供一套接口,客户是该软件的主要用户。该软件有助于为药房业务创建一个综合数据库,并根据到期、产品等各种参数提供各种报告…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

6.9本日总结
一、英语 复习默写list11list18,订正07年第3篇阅读 二、数学 学习线代第一讲,写15讲课后题 三、408 学习计组第二章,写计组习题 四、总结 明天结束线代第一章和计组第二章 五、明日计划 英语:复习l默写sit12list17&#…...

Linux 内存管理调试分析:ftrace、perf、crash 的系统化使用
Linux 内存管理调试分析:ftrace、perf、crash 的系统化使用 Linux 内核内存管理是构成整个内核性能和系统稳定性的基础,但这一子系统结构复杂,常常有设置失败、性能展示不良、OOM 杀进程等问题。要分析这些问题,需要一套工具化、…...

第2课 SiC MOSFET与 Si IGBT 静态特性对比
2.1 输出特性对比 2.2 转移特性对比 2.1 输出特性对比 器件的输出特性描述了当温度和栅源电压(栅射电压)为某一具体数值时,漏极电流(集电极电流...


