【数据结构】二叉树的顺序结构-堆
【数据结构】二叉树的顺序结构-堆
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
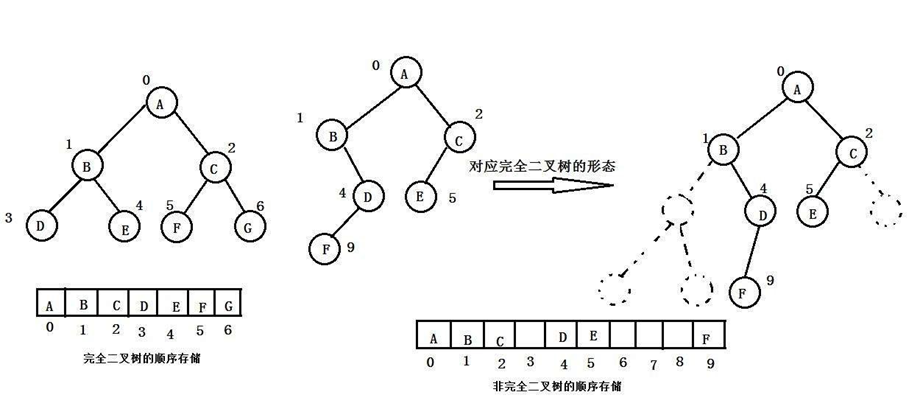
1.堆的概念及结构
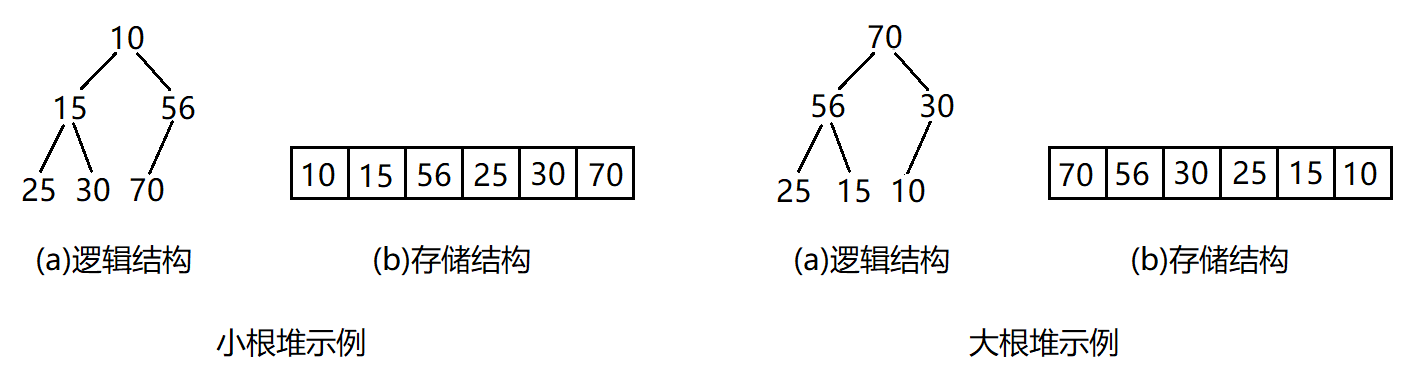
小堆:将根结点最小的堆叫做小堆,也叫最小堆或小根堆。
大堆:将根结点最大的堆叫做大堆,也叫最大堆或大根堆。
堆的性质:
- 堆中某个结点的值总是不大于或不小于其父结点的值。
- 堆总是一棵完全二叉树。
2.堆的实现
堆的向下调整算法
现在我们给出一个数组,逻辑上看作一棵完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。
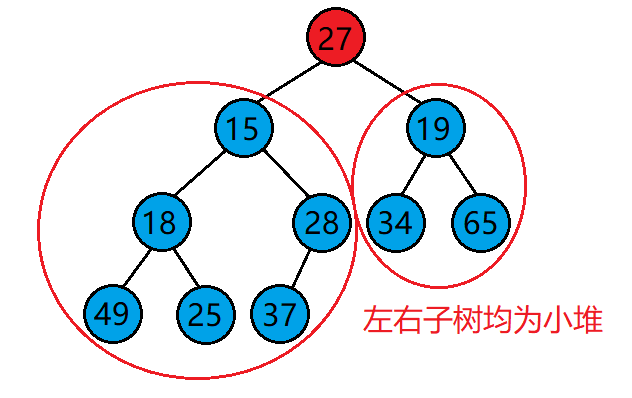
但是,使用向下调整算法需要满足一个前提:
- 若想将其调整为小堆,那么根结点的左右子树必须都为小堆。
- 若想将其调整为大堆,那么根结点的左右子树必须都为大堆。
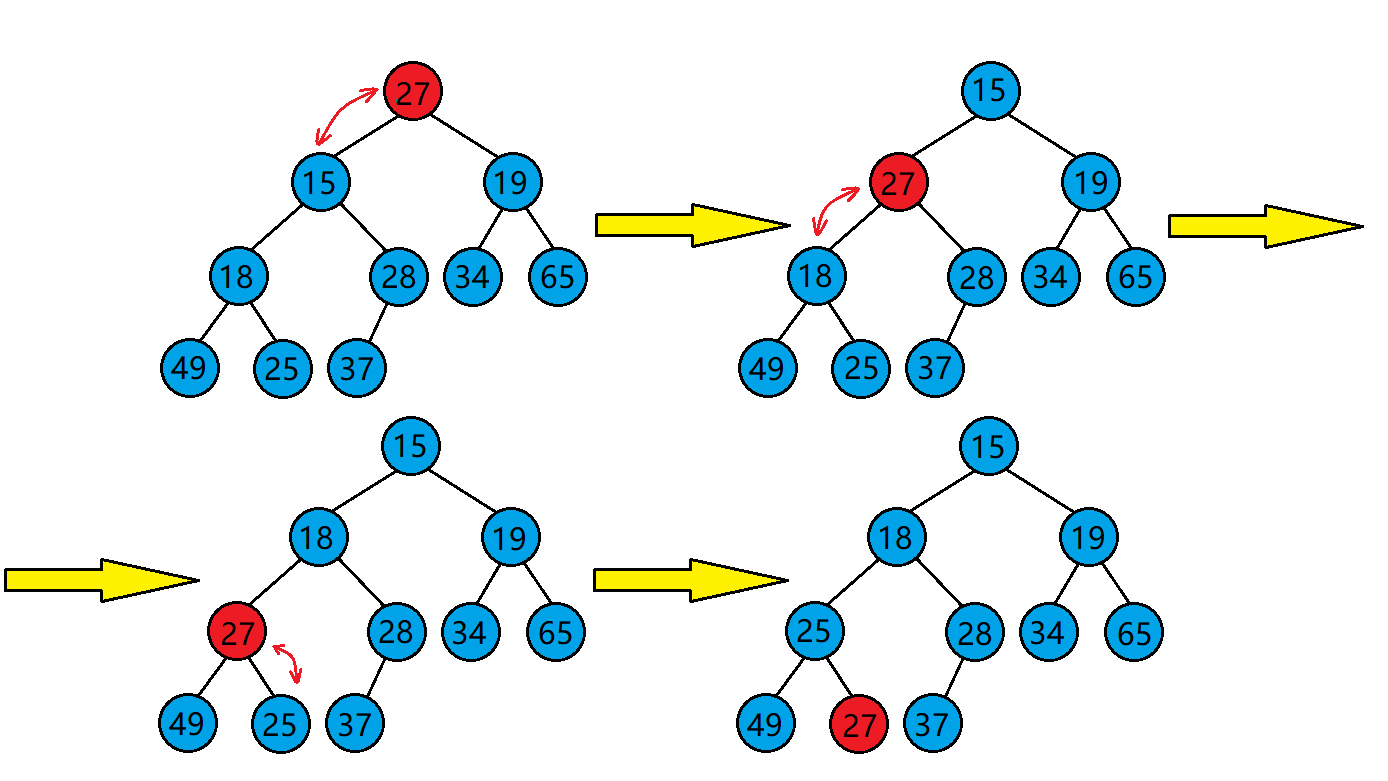
向下调整算法的基本思想(以建小堆为例):
- 从根结点处开始,选出左右孩子中值较小的孩子。
- 让小的孩子与其父亲进行比较。
- 若小的孩子比父亲还小,则该孩子与其父亲的位置进行交换。并将原来小的孩子的位置当成父亲继续向下进行调整,直到调整到叶子结点为止。
- 若小的孩子比父亲大,则不需处理了,调整完成,整个树已经是小堆了。
代码如下:
//交换函数
void Swap(int* x, int* y){int tmp = *x;*x = *y;*y = tmp;
}//堆的向下调整(小堆)
void AdjustDown(int *a, int n, int parent) {//child记录左右孩子中值较小的孩子的下标int child = 2 * parent + 1;//先默认其左孩子的值较小while (child < n) {if (child + 1 < n && a[child + 1] < a[child]){//右孩子存在并且右孩子比左孩子还小child++;//较小的孩子改为右孩子}if (a[child] < a[parent]){//左右孩子中较小孩子的值比父结点还小//将父结点与较小的子结点交换Swap(&a[child], &a[parent]);//继续向下进行调整parent = child;child = 2 * parent + 1;} else{//已成堆break;}}
}
使用堆的向下调整算法,最坏的情况下(即一直需要交换结点),需要循环的次数为:h - 1次(h为树的高度)。而h = log2(N+1)(N为树的总结点数)。所以堆的向下调整算法的时间复杂度为:O(logN) 。
上面说到,使用堆的向下调整算法需要满足其根结点的左右子树均为大堆或是小堆才行,那么如何才能将一个任意树调整为堆?
答案很简单,我们只需要从倒数第一个非叶子结点开始,从后往前,按下标,依次作为根去向下调整即可。
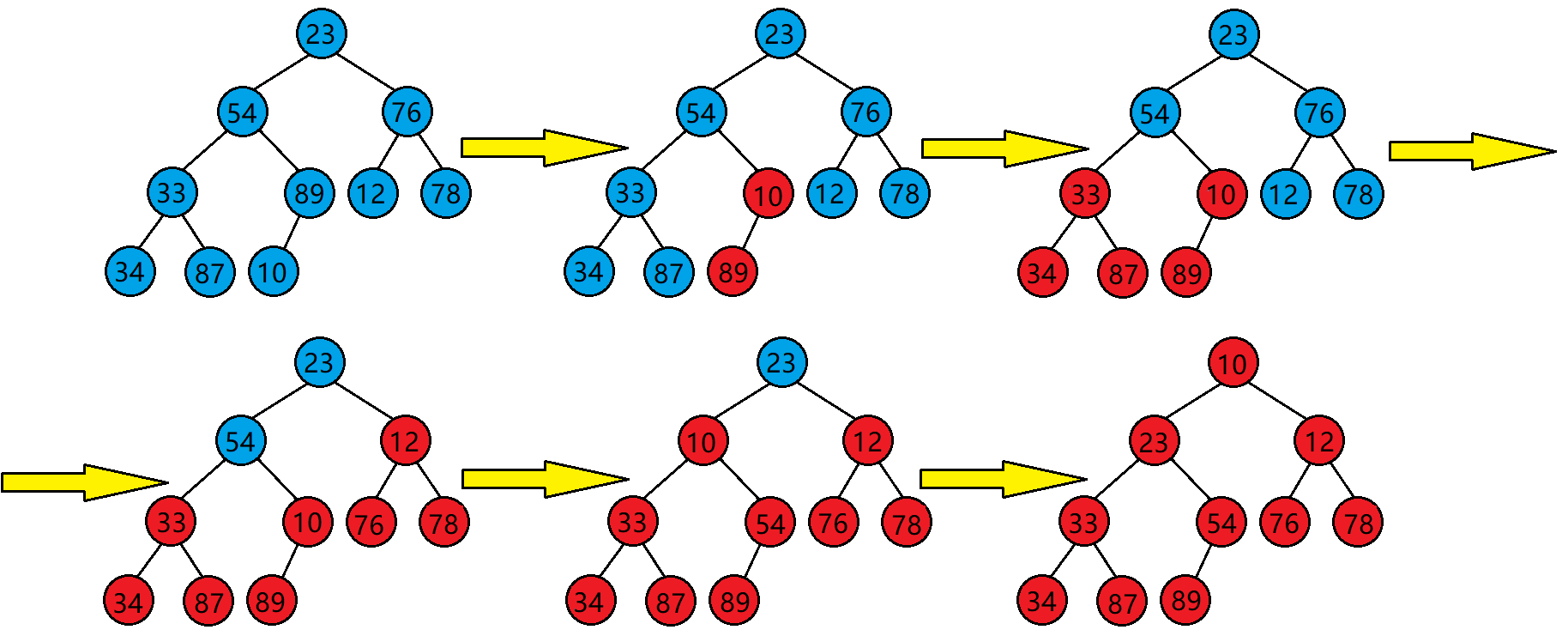
代码:
for (int i = (n - 1 - 1) / 2; i >= 0; i--) {AdjustDown(php->a, n, i);
}
那么建堆的时间复杂度又是多少呢?
当结点数无穷大时,完全二叉树与其层数相同的满二叉树相比较来说,它们相差的结点数可以忽略不计,所以计算时间复杂度的时候我们可以将完全二叉树看作与其层数相同的满二叉树来进行计算。
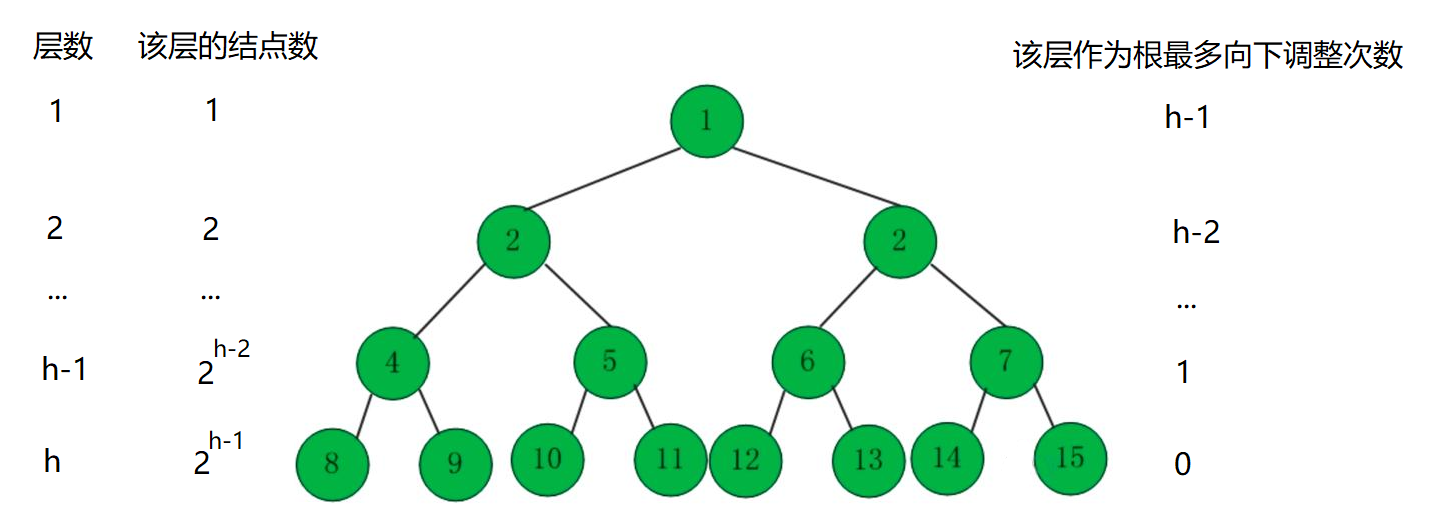
总结一下:
- 堆的向下调整算法的时间复杂度:T(n) = O (log N)
- 建堆的时间复杂度:T(n) = O(N)
堆的向上调整算法
当我们在一个堆的末尾插入一个数据后,需要对堆进行调整,使其仍然是一个堆,这时需要用到堆的向上调整算法。
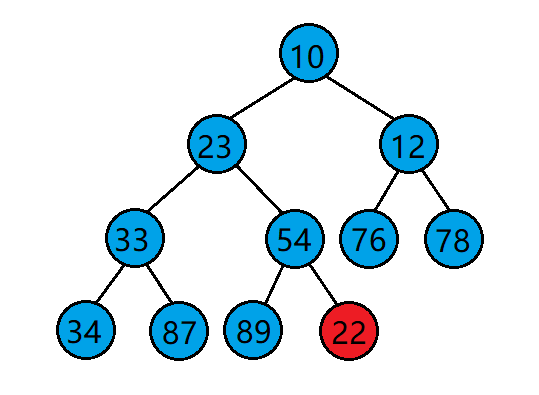
向上调整算法的基本思想(以建小堆为例):
- 将目标结点与其父结点比较。
- 若目标结点的值比其父结点的值小,则交换目标结点与其父结点的位置,并将原目标结点的父结点当作新的目标结点继续进行向上调整。若目标结点的值比其父结点的值大,则停止向上调整,此时该树已经是小堆了。
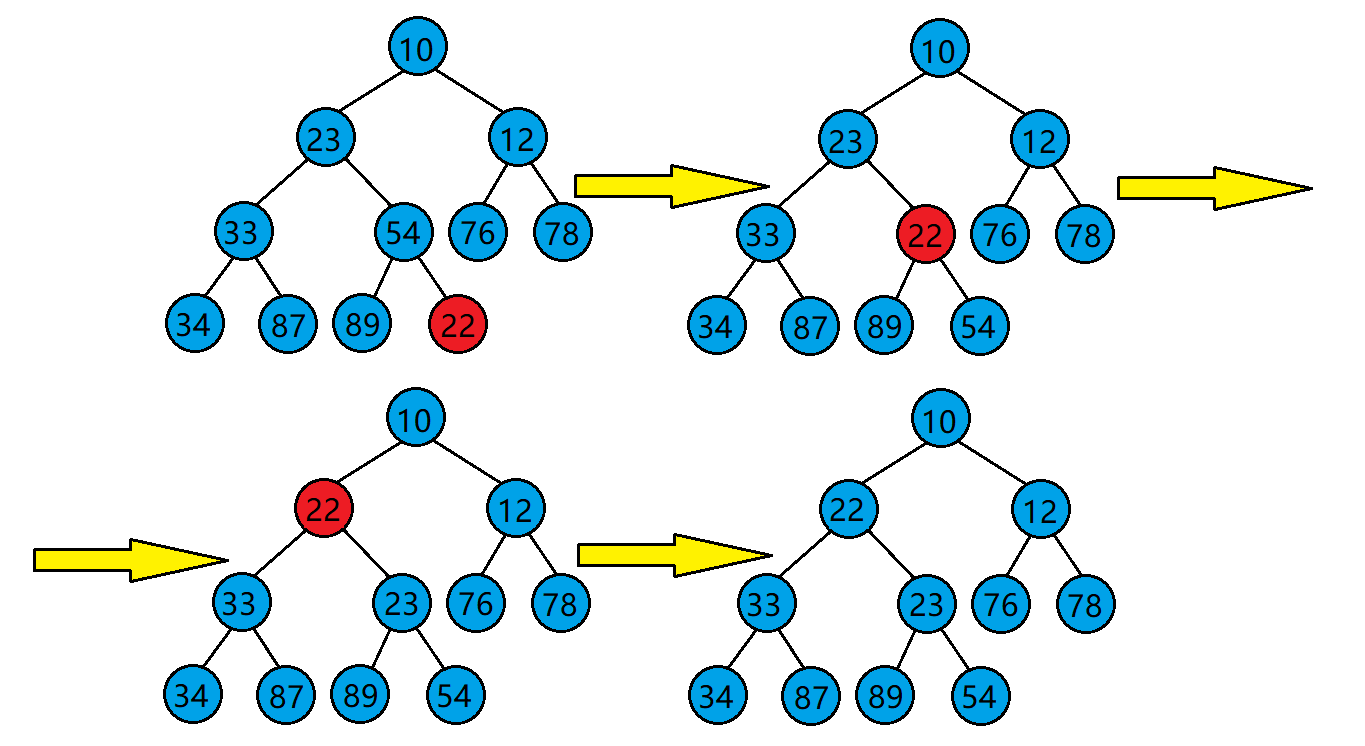
代码如下:
//交换函数
void Swap(HPDataType *x, HPDataType *y) {HPDataType tmp = *x;*x = *y;*y = tmp;
}//堆的向上调整(小堆)
void AdjustUp(HPDataType *a, int child) {int parent = (child - 1) / 2;while (child > 0) { //调整到根结点的位置截止if (a[child] < a[parent]) {//孩子结点的值小于父结点的值//将父结点与孩子结点交换Swap(&a[child], &a[parent]);//继续向上进行调整child = parent;parent = (child - 1) / 2;} else {//已成堆break;}}
}
初始化堆
首先,必须创建一个堆类型,该类型中需包含堆的基本信息:存储数据的数组、堆中元素的个数以及当前堆的最大容量。
typedef int HPDataType;
// 堆的结构 - 顺序表
typedef struct Heap {HPDataType *a;int size;int capacity;
} Heap;
建堆
然后我们需要一个建堆函数,对刚创建的堆进行初始化,注意在初始化期间要将传入数据建堆。
// 堆的创建 - 建堆算法
void HeapCreate(Heap *php, HPDataType *a, int n) {assert(php);php->a = (HPDataType *) realloc(php->a, sizeof(HPDataType) * n);if (php->a == NULL) {perror("realloc fail");exit(-1);}// 内存复制 数组复制到php->a中memcpy(php->a, a, sizeof(HPDataType) * n);php->size = php->capacity = n;// 建堆算法 - 从最后一个叶子节点的父亲节点开始向下调整,然后从父亲节点的前所有节点都向下调整一次// 最后节点的父亲的坐标是(n-1-1)/2 n-1因为n是节点个数,坐标从0开始for (int i = (n - 1 - 1) / 2; i >= 0; i--) {AdjustDown(php->a, n, i);}
}
销毁堆
为了避免内存泄漏,使用完动态开辟的内存空间后都要及时释放该空间,所以,一个用于释放内存空间的函数是必不可少的。
// 堆的销毁
void HeapDestroy(Heap *php) {assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}
打印堆
// 堆的打印
void HeapPrint(Heap *php) {assert(php);for (int i = 0; i < php->size; i++) {printf("%d ", php->a[i]);}printf("\n");
}
堆的插入
数据插入时是插入到数组的末尾,即树形结构的最后一层的最后一个结点,所以插入数据后我们需要运用堆的向上调整算法对堆进行调整,使其在插入数据后仍然保持堆的结构。
// 堆的插入
void HeapPush(Heap *php, HPDataType x) {assert(php);// 内存满了,扩容if (php->size == php->capacity) {int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType *tmp = (HPDataType *) realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL) {perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newcapacity;}// 插入php->a[php->size] = x;php->size++;// 插入完,开始向上调整建堆// 将数组和child的位置传过去AdjustUp(php->a, php->size - 1);
}
堆的删除
堆的删除,删除的是堆顶的元素,但是这个删除过程可并不是直接删除堆顶的数据,而是先将堆顶的数据与最后一个结点的位置交换,然后再删除最后一个结点,再对堆进行一次向下调整。
原因:我们若是直接删除堆顶的数据,那么原堆后面数据的父子关系就全部打乱了,需要全体重新建堆,时间复杂度为O(N) 。若是用上述方法,那么只需要对堆进行一次向下调整即可,因为此时根结点的左右子树都是小堆,我们只需要在根结点处进行一次向下调整即可,时间复杂度为O(log N)
// 堆的删除
void HeapPop(Heap *php) {assert(php);assert(php->size > 0);// 堆的删除,因为不能破坏堆的结构,所以将堆顶,和堆底最后一个数据交换,然后删除堆底,堆顶再向下调整,保持堆的结构// 1.交换堆顶和堆底Swap(&php->a[0], &php->a[php->size - 1]);// 2.删除堆底php->size--;// 3.向下调整AdjustDown(php->a, php->size, 0);
}
获取堆顶的数据
获取堆顶的数据,即返回数组下标为0的数据。
// 取堆顶
HPDataType HeapTop(Heap *php) {assert(php);assert(php->size > 0);return php->a[0];
}
获取堆的长度
获取堆的长度,即返回堆结构体中的size变量。
// 求堆的长度
size_t HeapSize(Heap *php) {assert(php);return php->size;
}
堆的判空
堆的判空,即判断堆结构体中的size变量是否为0。
// 堆的判空
bool HeapEmpty(Heap *php) {assert(php);return php->size == 0;
}
完整代码
#pragma once
#include <assert.h>
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>typedef int HPDataType;
// 堆的结构 - 顺序表
typedef struct Heap {HPDataType *a;int size;int capacity;
} Heap;// 堆的初始化
void HeapInit(Heap *php) {assert(php);php->a = NULL;php->size = php->capacity = 0;
}// 堆的打印
void HeapPrint(Heap *php) {assert(php);for (int i = 0; i < php->size; i++) {printf("%d ", php->a[i]);}printf("\n");
}// 堆的销毁
void HeapDestroy(Heap *php) {assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}// 向上调整 - 大堆
void AdjustUp(HPDataType *a, int child) {// 1.找父亲int parent = (child - 1) / 2;// 2.跟父亲比大小,如果是大堆,知道父亲大于孩子循环结束,如果一直小于孩子,一直交换,然后循环结束条件是child==0while (child > 0) {// 孩子大于父亲则交换if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;} else {break;}}
}// 向下调整 - 大堆
void AdjustDown(HPDataType *a, int n, int parent) {// 如果是大堆,先找父亲的孩子中的大的,然后跟他交换// 先假设左孩子是大的,如果不是,重新设置为右孩子是大的int child = parent * 2 + 1;// child的值不会越界,所以循环条件是child < nwhile (child < n) {// 重新设置最大的孩子,如果右孩子大,就++child。特殊情况:最后的节点,只有左孩子,没有右孩子,所以还要加条判断,左孩子+1<n说明还有一个右孩子if (child + 1 < n && a[child] < a[child + 1]) {child++;}// 1.父亲小于孩子,交换,继续向下调整// 2.父亲大于孩子,跳出if (a[parent] < a[child]) {Swap(&a[parent], &a[child]);// 交换后,重新设置parent,找下一个位置开始向下调整parent = child;child = parent * 2 + 1;} else {break;}}
}// 堆的插入
void HeapPush(Heap *php, HPDataType x) {assert(php);// 内存满了,扩容if (php->size == php->capacity) {int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType *tmp = (HPDataType *) realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL) {perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newcapacity;}// 插入php->a[php->size] = x;php->size++;// 插入完,开始向上调整建堆// 将数组和child的位置传过去AdjustUp(php->a, php->size - 1);
}// 堆的删除
void HeapPop(Heap *php) {assert(php);assert(php->size > 0);// 堆的删除,因为不能破坏堆的结构,所以将堆顶,和堆底最后一个数据交换,然后删除堆底,堆顶再向下调整,保持堆的结构// 1.交换堆顶和堆底Swap(&php->a[0], &php->a[php->size - 1]);// 2.删除堆底php->size--;// 3.向下调整AdjustDown(php->a, php->size, 0);
}// 取堆顶
HPDataType HeapTop(Heap *php) {assert(php);assert(php->size > 0);return php->a[0];
}// 求堆的长度
size_t HeapSize(Heap *php) {assert(php);return php->size;
}// 堆的判空
bool HeapEmpty(Heap *php) {assert(php);return php->size == 0;
}// 交换
void Swap(HPDataType *p1, HPDataType *p2) {HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}// 堆的创建 - 建堆算法
void HeapCreate(Heap *php, HPDataType *a, int n) {assert(php);php->a = (HPDataType *) realloc(php->a, sizeof(HPDataType) * n);if (php->a == NULL) {perror("realloc fail");exit(-1);}// 内存复制 数组复制到php->a中memcpy(php->a, a, sizeof(HPDataType) * n);php->size = php->capacity = n;// 建堆算法 - 从最后一个叶子节点的父亲节点开始向下调整,然后从父亲节点的前所有节点都向下调整一次// 最后节点的父亲的坐标是(n-1-1)/2 n-1因为n是节点个数,坐标从0开始for (int i = (n - 1 - 1) / 2; i >= 0; i--) {AdjustDown(php->a, n, i);}
}
3.堆的应用
堆排序
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
- 建堆
- 升序:建大堆
- 降序:建小堆
- 利用堆删除思想来进行排序建堆和堆删除中都用到了向下调整,因此掌握了向下调整,就可以完成堆排序。
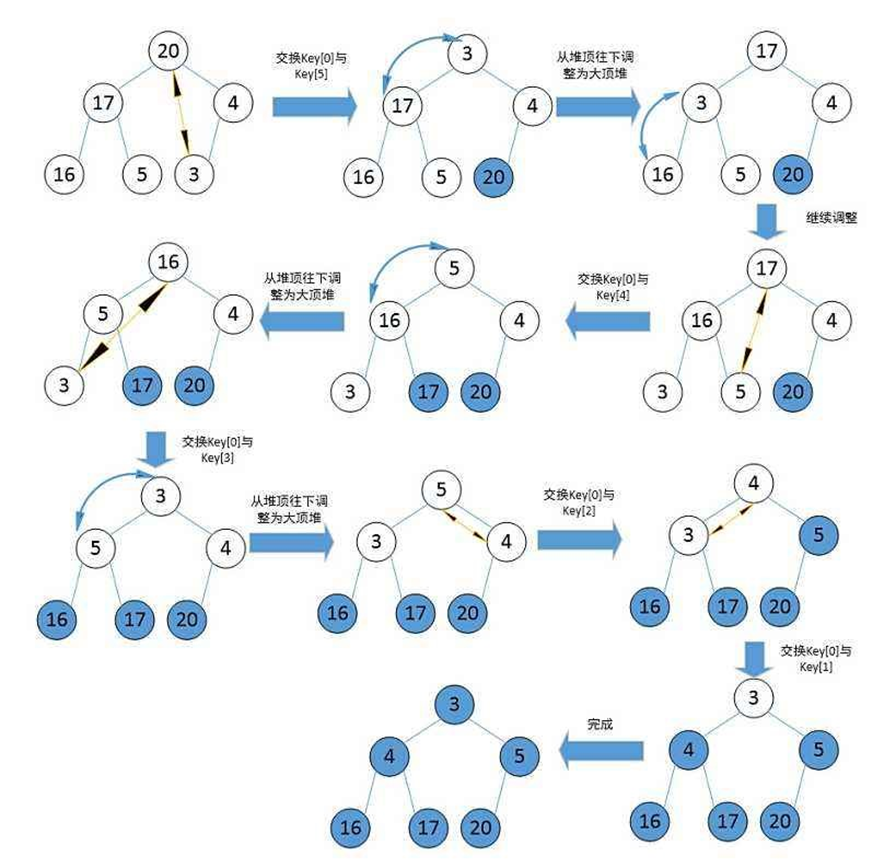
代码如下:
#include <stdio.h>
// 交换
void Swap(int *p1, int *p2) {int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// 向下调整 - 大堆
void AdjustDown(int *a, int n, int parent) {// 如果是大堆,先找父亲的孩子中的大的,然后跟他交换// 先假设左孩子是大的,如果不是,重新设置为右孩子是大的int child = parent * 2 + 1;// child的值不会越界,所以循环条件是child < nwhile (child < n) {// 重新设置最大的孩子,如果右孩子大,就++child。特殊情况:最后的节点,只有左孩子,没有右孩子,所以还要加条判断,左孩子+1<n说明还有一个右孩子if (child + 1 < n && a[child] < a[child + 1]) {child++;}// 1.父亲小于孩子,交换,继续向下调整// 2.父亲大于孩子,跳出if (a[parent] < a[child]) {Swap(&a[parent], &a[child]);// 交换后,重新设置parent,找下一个位置开始向下调整parent = child;child = parent * 2 + 1;} else {break;}}
}// 对数组进行堆排序
void HeapSort(int *a, int n) {// 向上调整建堆 -- N*logN/*for (int i = 1; i < n; ++i){AdjustUp(a, i);}*/// 向下调整建堆 - 大堆 O(N) _for (int i = (n - 1 - 1) / 2; i >= 0; i--) {AdjustDown(a, n, i);}int end = n - 1;while (end > 0) {// 第一个和最后一个交换,除了最后一个,剩下的进行建堆调整,把最大的调整到堆顶Swap(&a[0], &a[end]);// end为坐标,坐标比个数多一个,所以下面的end是剩余的个数AdjustDown(a, end, 0);end--;}
}int main() {int arr[10] = {32, 43, 56, 76, 84, 12, 45, 67, 43, 37};HeapSort(arr, sizeof(arr) / sizeof(int));for (int i = 0; i < sizeof(arr) / sizeof(int); i++) {printf("%d ", arr[i]);}
}
TOPK问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
- 用数据集合中前K个元素来建堆
- 前k个最大的元素,则建小堆
- 前k个最小的元素,则建大堆
- 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
//交换函数
void Swap(int *x, int *y) {int tmp = *x;*x = *y;*y = tmp;
}
//堆的向下调整(小堆)
void AdjustDown(int *a, int n, int parent) {//child记录左右孩子中值较小的孩子的下标int child = 2 * parent + 1;//先默认其左孩子的值较小while (child < n) {if (child + 1 < n && a[child + 1] < a[child]) {//右孩子存在并且右孩子比左孩子还小child++; //较小的孩子改为右孩子}if (a[child] < a[parent]) {//左右孩子中较小孩子的值比父结点还小//将父结点与较小的子结点交换Swap(&a[child], &a[parent]);//继续向下进行调整parent = child;child = 2 * parent + 1;} else {//已成堆break;}}
}int *getLeastNumbers(int *arr, int arrSize, int k, int *returnSize) {*returnSize = k;if (k == 0)return NULL;//用数组的前K个数建小堆int i = 0;int *retArr = (int *) malloc(sizeof(int) * k);for (i = 0; i < k; i++) {retArr[i] = arr[i];}for (i = (k - 1 - 1) / 2; i >= 0; i--) {AdjustDown(retArr, k, i);}//剩下的N-k个数依次与堆顶数据比较for (i = k; i < arrSize; i++) {if (arr[i] > retArr[0]) {retArr[0] = arr[i];//堆顶数据替换}AdjustDown(retArr, k, 0);//进行一次向下调整}return retArr;//返回最大的k个数
}
时间复杂度:O(k + N * log k)空间复杂度:O(k)
相关文章:

【数据结构】二叉树的顺序结构-堆
【数据结构】二叉树的顺序结构-堆 普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间…...

2024年java面试--mysql(2)
系列文章目录 2024年java面试(一)–spring篇2024年java面试(二)–spring篇2024年java面试(三)–spring篇2024年java面试(四)–spring篇2024年java面试–集合篇2024年java面试–redi…...

IllegalArgumentException
Caused by: java.lang.IllegalArgumentException:Invalid pulsar service : persistent 参数非法异常 这个异常是由于使用了无效的 Pulsar 服务类型导致的。Pulsar 支持不同的服务类型,例如 persistent、non-persistent 等。 当你在配置 Pulsar 相关的参数时&…...
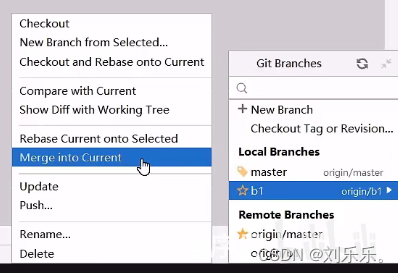
Git 概述命令、idea中的使用
目录 Git概述 Git代码托管服务 Git常用命令 Git 全局设置 获取 Git 仓库 编辑Git 工作区中文件的状态 本地仓库操作 远程仓库操作 编辑分支操作 标签操作 在IDEA中使用Git 1.获取Git仓库 .gitignore 表示忽略 2.本地仓库操作 3.远程仓库操作 4.分支操作 Git是…...
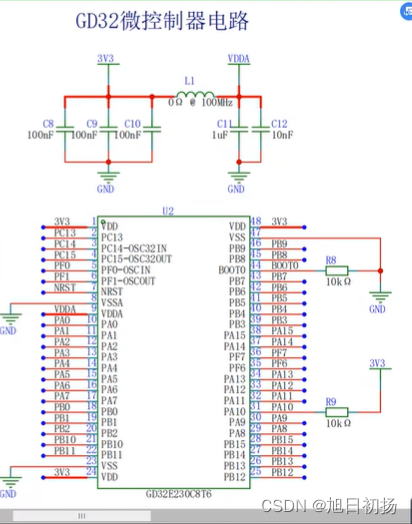
单片机之硬件记录
一、概念 VBAT 当使用电池或其他电源连接到VBAT脚上时,当VDD断电时,可以保存备份寄存器的内容和维持RTC的功能。如果应用中没有使用外部电池,VBAT引脚应接到VDD引脚上。 VCC:Ccircuit 表示电路的意思,即接入电路的电压&#x…...

QQ文件传输协议研究
引言 我们都知道,现在越来越多的应用采取了 HTTPS or TLS 传输协议,对于一般的协议,我们可以使用中间人技术对流量进行劫持转发,从而破解密文,这边可以参见我的另外一篇文章基于加密邮件协议的中间人攻防实战, 而对于 HTTPS 应用即使是我们采取中间人技术,也很难让浏览器…...

Qt/C++音视频开发51-推流到各种流媒体服务程序
一、前言 最近将推流程序完善了很多功能,尤其是增加了对多种流媒体服务程序的支持,目前支持mediamtx、LiveQing、EasyDarwin、nginx-rtmp、ZLMediaKit、srs、ABLMediaServer等,其中经过大量的对比测试,个人比较建议使用mediamtx和ZLMediaKit,因为这两者支持的格式众多,不…...

LeetCode 35. 搜索插入位置
题目链接 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目解析 该题我们可以采用二分查找的方式,我们可以把数组分为,小于target的一边儿和大于等于target的一边儿。 当midleft(right-left)下标所对应的数大于等于targ…...

7年经验之谈 —— Web测试是什么,有何特点?
Web测试是指对Web应用程序进行验证和评估的过程,以确保其功能、性能和安全性符合预期。 Web测试具体包括以下几个方面的内容: 功能测试:验证Web应用程序是否按照需求规格说明书中定义的功能正常工作。功能测试包括输入验证、表单提交、页面…...

【数据结构】前言概况 - 树
🚩纸上得来终觉浅, 绝知此事要躬行。 🌟主页:June-Frost 🚀专栏:数据结构 🔥该文章针对树形结构作出前言,以保证可以对树初步认知。 目录: 🌍前言:dz…...
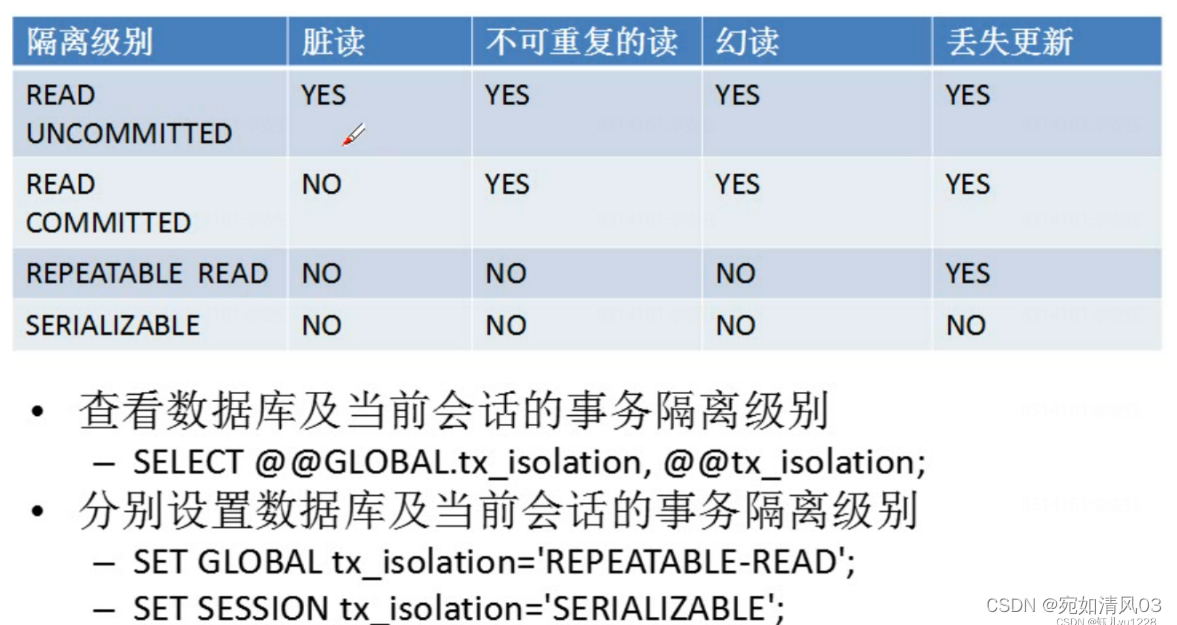
MySQL——事务
一、事务的开始与结束 一个数据库事务由一条或多条sql语句构成,它们形成一个逻辑的工作单元。这些sql语句要么全部执行成功,要么全部执行失败。 1.1.事物的开始 1.对于DDL(create,alter,drop)和DCL&…...
虚拟机Ubuntu操作系统最基本终端命令(安装包+详细解释+详细演示)
虚拟机及乌班图(Ubuntu操作系统) 提示:大家需要软件的可以直接在此链接中提取 链接:https://pan.baidu.com/s/1_4VHGTlXjIuVhBINeOuBCA 提取码:nd0c 文章目录 虚拟机及乌班图(Ubuntu操作系统)终…...

Android 11.0 当系统内置两个Launcher时默认设置Launcher3以外的那个Launcher为默认Launcher
1.概述 在11.0定制化开发中,由于产品开发需要要求系统内置两个Launcher,一个是Launcher3,一个是自己开发的Launcher,当系统启动Launcher时, 不要弹出Launcher选择列表 选择哪个Launcher要求默认选择自己开发的Launcher作为默认Launcher,关于选择Launcher列表 其实都是在Res…...

NO5.心愿打印机
def light():#定义一个函数,以:结尾print(红灯2)#打印print(绿灯3)#打印 print(黄灯1)#和def顶格,先执行 light()#调用light函数【PDF转Word】 https://fzqxk86ywz.feishu.cn/sheets/GugIsI9zKhNaEwtJscbcgKFCn6b 【Fiddler汉化】 https://fzqxk86ywz.f…...

cudart.so vs cuda.so的区别
libcuda.so provides access to the CUDA driver API, whereas libcudart.so provides access to the CUDA runtime API. libcuda.so提供对CUDA驱动程序API的访问,而libcuart.so提供了对CUDA运行时API的访问。 在wsl中cuda.so位于/usr/lib/wsl/lib/libcuda.so 可以…...

Oracle集群管理-19C集群禁用numa和大页内存特性
Linux Redhat 7.9关闭内存管理特性 1 关闭大页内存 [rootdb1 ~]# cat /sys/kernel/mm/transparent_hugepage/defrag [always] madvise never [rootdb1 ~]# cat /sys/kernel/mm/transparent_hugepage/enabled [always] madvise never echo never > /sys/kernel/mm/transpare…...

题目:2726.使用方法链的计算器
题目来源: leetcode题目,网址:2726. 使用方法链的计算器 - 力扣(LeetCode) 解题思路: 按要求模拟,在计算后返回自己以达到链式调用的目的。 解题代码: class Calculator {/**…...

基于ASP.NET的驾校管理系统设计与实现
摘 要 伴随国民经济的飞速发展和人民生活水平的不断提高,家用汽车在我国逐渐普及。面对不断增长的庞大的用户群,随之产生的驾驶培训行业,规模不断扩大。近年来,随着Internet的迅速发展以及网页制作技术的日臻完善,驾校…...

第一章 计算机系统概述 三、操作系统的发展与分类
一、手工操作阶段 缺点:人机速度矛盾 二、批处理阶段 1、单道批处理系统(引入脱机输入输出技术) 优点:缓解人机速度矛盾 缺点:资源利用率依然很低 2、多道批处理系统(操作系统开始出现) 优点:多道程序并发进行,…...
【2023年11月第四版教材】第12章《质量管理》(第二部分)
第12章《质量管理》(第二部分) 4 规划质量管理4.1 数据收集★★★4.2 数据分析★★★4.3 数据表现★★★4.4 质量管理计划★★★4.5 质量测量指标★★★ (22下35) 4 规划质量管理 组过程输入工具和技术输出计划1.规划质量管理1.项…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
