机器学习(10)---特征选择
文章目录
- 一、概述
- 二、Filter过滤法
- 2.1 过滤法说明
- 2.2 方差过滤
- 2.3 方差过滤对模型影响
- 三、相关性过滤
- 3.1 卡方过滤
- 3.2 F检验
- 3.3 互信息法
- 3.4 过滤法总结
- 四、Embedded嵌入法
- 4.1 嵌入法说明
- 4.2 以随机森林为例的嵌入法
- 五、Wrapper包装法
- 5.1 包装法说明
- 5.2 以随机森林为例的包装法
- 六、总结
一、概述
1. 从所有的特征中,选择出有意义,对模型有帮助的特征,以避免必须将所有特征都导入模型去训练的情况。
2. 我们来看一组数据:
import pandas as pd
data = pd.read_csv(r"D:\Download\digit recognizor.csv")
X = data.iloc[:,1:]
y = data.iloc[:,0]
print(X.shape)

注:这个数据量相对夸张,如果使用支持向量机和神经网络,很可能会直接跑不出来。使用KNN跑一次大概需要半个小时。用这个数据举例,能更够体现特征选择的重要性。
二、Filter过滤法
2.1 过滤法说明
1. 过滤方法通常用作预处理步骤,特征选择完全独立于任何机器学习算法。它是根据各种统计检验中的分数以及相关性的各项指标来选择特征。
2. 处理步骤图:

2.2 方差过滤
1. 这是通过特征本身的方差来筛选特征的类。比如一个特征本身的方差很小,就表示样本在这个特征上基本没有差异,可能特征中的大多数值都一样,甚至整个特征的取值都相同,那这个特征对于样本区分没有什么作用。所以无论接下来的特征工程要做什么,都要优先消除方差为0的特征。VarianceThreshold有重要参数threshold,表示方差的阈值,表示舍弃所有方差小于threshold的特征,不填默认为0,即删除所有的记录都相同的特征。
2. 处理上面数据:
from sklearn.feature_selection import VarianceThreshold
selector = VarianceThreshold() #实例化,不填参数默认方差为0
X_var0 = selector.fit_transform(X) #获取删除不合格特征之后的新特征矩阵
#也可以直接写成 X = VairanceThreshold().fit_transform(X)
print(X_var0.shape)

注意:我们可以看到特征数量已经由784变为了708。但是依然剩下了708多个特征,明显还需要进一步的特征选择。然而,如果我们知道我们需要多少个特征,方差也可以帮助我们将特征选择一步到位。比如说,我们希望留下一半的特征,那可以设定一个让特征总数减半的方差阈值,只要找到特征方差的中位数,再将这个中位数作为参数threshold的值输入就好了,如下面代码块:
import numpy as np
X_fsvar = VarianceThreshold(np.median(X.var().values)).fit_transform(X)
X.var().values
np.median(X.var().values)
print(X_fsvar.shape)
2.3 方差过滤对模型影响
1. KNN方差过滤前后:
import pandas as pd
from sklearn.feature_selection import VarianceThreshold
from sklearn.neighbors import KNeighborsClassifier as KNN
from sklearn.model_selection import cross_val_score
import numpy as np
X = data.iloc[:,1:]
y = data.iloc[:,0]
X_fsvar = VarianceThreshold(np.median(X.var().values)).fit_transform(X)#======【TIME WARNING:35mins +】======#
print(cross_val_score(KNN(),X,y,cv=5).mean())#======【TIME WARNING:4 hours】======#
print(cross_val_score(KNN(),X,y,cv=5).mean())


2. 随机森林方差过滤前后:
import pandas as pd
from sklearn.feature_selection import VarianceThreshold
import numpy as np
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifier as RFC
X_fsvar = VarianceThreshold(np.median(X.var().values)).fit_transform(X)
print(cross_val_score(RFC(n_estimators=10,random_state=0),X,y,cv=5).mean())
print(cross_val_score(RFC(n_estimators=10,random_state=0),X_fsvar,y,cv=5).mean())

注解:(1)首先可以观察到的是,随机森林的准确率略逊于KNN,但运行时间却连KNN的1%都不到,只需要十几秒钟。其次,方差过滤后,随机森林的准确率也微弱上升,但运行时间却几乎是没什么变化,依然是11秒钟。
(2)为什么随机森林运行如此之快?为什么方差过滤对随机森林没很大的有影响?这是由于两种算法的原理中涉及到的计算量不同。
(3)最近邻算法KNN,单棵决策树,支持向量机SVM,神经网络,回归算法,都需要遍历特征或升维来进行运算,所以他们本身的运算量就很大,需要的时间就很长,因此方差过滤这样的特征选择对他们来说就尤为重要。但对于不需要遍历特征的算法,比如随机森林,它随机选取特征进行分枝,本身运算就非常快速,因此特征选择对它来说效果平平。这其实很容易理解,无论过滤法如何降低特征的数量,随机森林也只会选取固定数量的特征来建模;而最近邻算法就不同了,特征越少,距离计算的维度就越少,模型明显会随着特征的减少变得轻量。因此,过滤法的主要对象是:需要遍历特征或升维的算法们,而过滤法的主要目的是:在维持算法表现的前提下,帮助算法们降低计算成本。
3. 对受影响的算法(如KNN)来说,我们可以将方差过滤的影响总结如下:
| 阈值很小,被过滤掉得特征比较少 | 阈值比较大,被过滤掉的特征有很多 | |
|---|---|---|
| 模型表现 | 不会有太大影响 | 可能变更好,代表被滤掉的特征大部分是噪音;也可能变糟糕,代表被滤掉的特征中很多都是有效特征 |
| 运行时间 | 可能降低模型的运行时间,基于方差很小的特征有多少;当方差很小的特征不多时对模型没有太大影响 | 一定能够降低模型的运行时间,算法在遍历特征时的计算越复杂,运行时间下降得越多 |
三、相关性过滤
方差挑选完毕之后,我们就要考虑下一个问题:相关性了。我们希望选出与标签相关且有意义的特征,因为这样的特征能够为我们提供大量信息。如果特征与标签无关,那只会白白浪费我们的计算内存,可能还会给模型带来噪音。在sklearn当中,我们有三种常用的方法来评判特征与标签之间的相关性:卡方,F检验,互信息。
3.1 卡方过滤
1. 卡方过滤是专门针对离散型标签(即分类问题)的相关性过滤。卡方检验类feature_selection.chi2计算每个非负特征和标签之间的卡方统计量,并依照卡方统计量由高到低为特征排名。再结合feature_selection.SelectKBest这个可以输入”评分标准“来选出前K个分数最高的特征的类,我们可以借此除去最可能独立于标签,与我们分类目的无关的特征。
2. 另外,如果卡方检验检测到某个特征中所有的值都相同,会提示我们使用方差先进行方差过滤。并且,刚才我们已经验证过,当我们使用方差过滤筛选掉一半的特征后,模型的表现时提升的。因此在这里,我们使用threshold=中位数时完成的方差过滤的数据来做卡方检验(如果方差过滤后模型的表现反而降低了,那我们就不会使用方差过滤后的数据,而是使用原数据)。
3. 代码块举例:
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
#假设在这里我一直我需要300个特征
X_fschi = SelectKBest(chi2, k=300).fit_transform(X_fsvar, y)
print(X_fschi.shape) #输出(42000,300)
cross_val_score(RFC(n_estimators=10,random_state=0),X_fschi,y,cv=5).mean()

注解:可以看出,模型的效果降低了,这说明我们在设定k=300的时候删除了与模型相关且有效的特征,我们的K值设置得太小,要么我们需要调整K值,要么我们必须放弃相关性过滤。当然,如果模型的表现提升,则说明我们的相关性过滤是有效的,是过滤掉了模型的噪音的,这时候我们就保留相关性过滤的结果。
3.2 F检验
1. F检验,又称ANOVA,方差齐性检验,是用来捕捉每个特征与标签之间的线性关系的过滤方法。它即可以做回归也可以做分类,因此包含feature_selection.f_classif(F检验分类)和feature_selection.f_regression(F检验回归)两个类。其中F检验分类用于标签是离散型变量的数据,而F检验回归用于标签是连续型变量的数据。
2. 和卡方检验一样,这两个类需要和类SelectKBest连用,并且我们也可以直接通过输出的统计量来判断我们到底要设置一个什么样的K。需要注意的是,F检验在数据服从正态分布时效果会非常稳定,因此如果使用F检验过滤,我们会先将数据转换成服从正态分布的方式。
3. 代码块举例:
from sklearn.feature_selection import f_classif
F, pvalues_f = f_classif(X_fsvar,y)
k = F.shape[0] - (pvalues_f > 0.05).sum() #392
X_fsF = SelectKBest(f_classif, k=392).fit_transform(X_fsvar, y)
print(cross_val_score(RFC(n_estimators=10,random_state=0),X_fsF,y,cv=5).mean())

注解:所有的特征都是和标签相关的,因此我们不需要相关性过滤。
3.3 互信息法
1. 互信息法是用来捕捉每个特征与标签之间的任意关系(包括线性和非线性关系)的过滤方法。和F检验相似,它既可以做回归也可以做分类,并且包含两个类feature_selection.mutual_info_classif(互信息分类)和feature_selection.mutual_info_regression(互信息回归)。这两个类的用法和参数都和F检验一模一样,不过互信息法比F检验更加强大,F检验只能够找出线性关系,而互信息法可以找出任意关系。
2. 互信息法不返回p值或F值类似的统计量,它返回“每个特征与目标之间的互信息量的估计”,这个估计量在[0,1]之间取值,为0则表示两个变量独立,为1则表示两个变量完全相关。
3. 代码块举例:
from sklearn.feature_selection import mutual_info_classif as MIC
result = MIC(X_fsvar,y)
k = result.shape[0] - sum(result <= 0)
X_fsmic = SelectKBest(MIC, k=填写具体的k).fit_transform(X_fsvar, y)
print(cross_val_score(RFC(n_estimators=10,random_state=0),X_fsmic,y,cv=5).mean())
注解:所有特征的互信息量估计都大于0,因此所有特征都与标签相关。
3.4 过滤法总结
到这里我们学习了常用的基于过滤法的特征选择,包括方差过滤,基于卡方,F检验和互信息的相关性过滤。通常来说,我会建议,先使用方差过滤,然后使用互信息法来捕捉相关性,不过了解各种各样的过滤方式也是必要的。所有信息被总结在下表:
| 类 | 说明 | 超参数的选择 |
|---|---|---|
| VarianceThreshold | 方差过滤,可输入方差阈值,返回方差大于阈值的新特征矩阵 | 看具体数据究竟是含有更多噪声还是更多有效特征,一般就使用0或1来筛选,也可以画学习曲线或取中位数 |
| SelectKBest | 用来选取K个统计量结果最佳的特征,生成符合统计量要求的新特征矩阵 | 看配合使用的统计量 |
| chi2 | 卡方检验,专用于分类算法,捕捉相关性 | 追求p小于显著性水平的特征 |
| f_classif | F检验分类,只能捕捉线性相关性,要求数据服从正态分布 | 追求p小于显著性水平的特征 |
| f_regression | F检验回归,只能捕捉线性相关性,要求数据服从正态分布 | 追求p小于显著性水平的特征 |
| mutual_info_classif | 互信息分类,可以捕捉任何相关性,不能用于稀疏矩阵 | 追求互信息估计大于0的特征 |
| mutual_info_regression | 互信息回归,可以捕捉任何相关性不能用于稀疏矩阵 | 追求互信息估计大于0的特征 |
四、Embedded嵌入法
4.1 嵌入法说明
1. (1)嵌入法是一种让算法自己决定使用哪些特征的方法,即特征选择和算法训练同时进行。(2)在使用嵌入法时,我们先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据权值系数从大到小选择特征。这些权值系数往往代表了特征对于模型的某种贡献或某种重要性,比如决策树和树的集成模型中的feature_importances_属性,可以列出各个特征对树的建立的贡献,我们就可以基于这种贡献的评估,找出对模型建立最有用的特征。(3)因此相比于过滤法,嵌入法的结果会更加精确到模型的效用本身,对于提高模型效力有更好的效果。并且,由于考虑特征对模型的贡献,因此无关的特征(需要相关性过滤的特征)和无区分度的特征(需要方差过滤的特征)都会因为缺乏对模型的贡献而被删除掉,可谓是过滤法的进化版。

2. 然而,嵌入法也不是没有缺点:过滤法中使用的统计量可以使用统计知识和常识来查找范围(如p值应当低于显著性水平0.05),而嵌入法中使用的权值系数却没有这样的范围可找——我们可以说,权值系数为0的特征对模型丝毫没有作用,但当大量特征都对模型有贡献且贡献不一时,我们就很难去界定一个有效的临界值。这种情况下,模型权值系数就是我们的超参数,我们或许需要学习曲线,或者根据模型本身的某些性质去判断这个超参数的最佳值究竟应该是多少。
注解:在机器学习中,超参数(hyperparameters)是指在模型训练过程中需要手动设置的参数,而不是由模型自动学习得到的参数。这些超参数通常用于控制模型的学习过程和性能。与超参数相对的是模型参数(model parameters),它们是模型自动学习得到的参数,例如权重和偏置。
3. 模块:feature_selection.SelectFromModel(estimator, threshold=None, prefit=False, norm_order=1,max_features=None)
SelectFromModel是一个元变换器,可以与任何在拟合后具有coef_,feature_importances_属性或参数中可选惩罚项的评估器一起使用(比如随机森林和树模型就具有属性、feature_importances_,逻辑回归就带有l1和l2惩罚项,线性支持向量机也支持l2惩罚项)。
对于有feature_importances_的模型来说,若重要性低于提供的阈值参数,则认为这些特征不重要并被移除。feature_importances_的取值范围是[0,1],如果设置阈值很小,比如0.001,就可以删除那些对标签预测完全没贡献的特征。如果设置得很接近1,可能只有一两个特征能够被留下。
选读:使用惩罚项的模型的嵌入法。
对于使用惩罚项的模型来说,正则化惩罚项越大,特征在模型中对应的系数就会越小。当正则化惩罚项大到一定的程度的时候,部分特征系数会变成0,当正则化惩罚项继续增大到一定程度时,所有的特征系数都会趋于0。但是我们会发现一部分特征系数会更容易先变成0,这部分系数就是可以筛掉的。也就是说,我们选择特征系数较大的特征。另外,支持向量机和逻辑回归使用参数C来控制返回的特征矩阵的稀疏性,参数C越小,返回的特征越少。Lasso回归,用alpha参数来控制返回的特征矩阵,alpha的值越大,返回的特征越少。
| 参数 | 说明 |
|---|---|
| estimator | 使用的模型评估器,只要是带feature_importances_或者coef_属性,或带有l1和l2惩罚项的模型都可以使用 |
| threshold | 特征重要性的阈值,重要性低于这个阈值的特征都将被删除 |
| prefit | 默认False,判断是否将实例化后的模型直接传递给构造函数。如果为True,则必须直接调用fit和transform,不能使用fit_transform,并且SelectFromModel不能与cross_val_score,GridSearchCV和克隆估计器的类似实用程序一起使用。 |
| norm_order | k可输入非零整数,正无穷,负无穷,默认值为1,在评估器的coef_属性高于一维的情况下,用于过滤低于阈值的系数的向量的范数的阶数。 |
| max_features | 在阈值设定下,要选择的最大特征数。要禁用阈值并仅根据max_features选择,请设置threshold = -np.inf |
注意:我们重点要考虑的是前两个参数。
4.2 以随机森林为例的嵌入法
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestClassifier as RFC
RFC_ = RFC(n_estimators =10,random_state=0)
X_embedded = SelectFromModel(RFC_,threshold=0.005).fit_transform(X,y)
#在这里我只想取出来有限的特征。0.005这个阈值对于有780个特征的数据来说,是非常高的阈值,因为平均每个特征
只能够分到大约0.001的feature_importances_
X_embedded.shape
#模型的维度明显被降低了
#同样的,我们也可以画学习曲线来找最佳阈值
#======【TIME WARNING:10 mins】======#
import numpy as np
import matplotlib.pyplot as plt
RFC_.fit(X,y).feature_importances_
threshold = np.linspace(0,(RFC_.fit(X,y).feature_importances_).max(),20)
score = []
for i in threshold:X_embedded = SelectFromModel(RFC_,threshold=i).fit_transform(X,y)once = cross_val_score(RFC_,X_embedded,y,cv=5).mean()score.append(once)
plt.plot(threshold,score)
plt.show()

注解:从图像上来看,随着阈值越来越高,模型的效果逐渐变差,被删除的特征越来越多,信息损失也逐渐变大。但是在0.00134之前,模型的效果都可以维持在0.93以上,因此我们可以从中挑选一个数值来验证一下模型的效果。
X_embedded = SelectFromModel(RFC_,threshold=0.00067).fit_transform(X,y)X_embedded.shape
cross_val_score(RFC_,X_embedded,y,cv=5).mean()
注解:可以看出,特征个数瞬间缩小到324多,这比我们在方差过滤的时候选择中位数过滤出来的结果392列要小,并且交叉验证分数0.9399高于方差过滤后的结果0.9388,这是由于嵌入法比方差过滤更具体到模型的表现的缘故,换一个算法,使用同样的阈值,效果可能就没有这么好了。和其他调参一样,我们可以在第一条学习曲线后选定一个范围,使用细化的学习曲线来找到最佳值。
#======【TIME WARNING:10 mins】======#
score2 = []
foriinnp.linspace(0,0.00134,20):X_embedded = SelectFromModel(RFC_,threshold=i).fit_transform(X,y) once = cross_val_score(RFC_,X_embedded,y,cv=5).mean()score2.append(once)
plt.figure(figsize=[20,5])
plt.plot(np.linspace(0,0.00134,20),score2)
plt.xticks(np.linspace(0,0.00134,20))
plt.show()

注解:查看结果,果然0.00067并不是最高点,真正的最高点0.000564已经将模型效果提升到了94%以上。
#=====【TIME WARNING:2 min】=====#
#我们可能已经找到了现有模型下的最佳结果,如果我们调整一下随机森林的参数呢?
cross_val_score(RFC(n_estimators=100,random_state=0),X_embedded,y,cv=5).mean()
注解:得出的特征数目依然小于方差筛选,并且模型的表现也比没有筛选之前更高,已经完全可以和计算一次半小时的KNN相匹敌(KNN的准确率是96.58%),接下来再对随机森林进行调参,准确率应该还可以再升高不少。可见,在嵌入法下,我们很容易就能够实现特征选择的目标:减少计算量,提升模型表现。因此,比起要思考很多统计量的过滤法来说,嵌入法可能是更有效的一种方法。然而,在算法本身很复杂的时候,过滤法的计算远远比嵌入法要快,所以大型数据中,我们还是会优先考虑过滤法。
五、Wrapper包装法
5.1 包装法说明
1. 装法也是一个特征选择和算法训练同时进行的方法,与嵌入法十分相似,它也是依赖于算法自身的选择,比如coef_属性或feature_importances_属性来完成特征选择。但不同的是,我们往往使用一个目标函数作为黑盒来帮助我们选取特征,而不是自己输入某个评估指标或统计量的阈值。包装法在初始特征集上训练评估器,并且通过coef_属性或通过feature_importances_属性获得每个特征的重要性。然后,从当前的一组特征中修剪最不重要的特征。在修剪的集合上递归地重复该过程,直到最终到达所需数量的要选择的特征。区别于过滤法和嵌入法的一次训练解决所有问题,包装法要使用特征子集进行多次训练,因此它所需要的计算成本是最高的。

2. 注意:在这个图中的“算法”,指的不是我们最终用来导入数据的分类或回归算法(即不是随机森林),而是专业的数据挖掘算法,即我们的目标函数。这些数据挖掘算法的核心功能就是选取最佳特征子集。
3. 最典型的目标函数是递归特征消除法(Recursive feature elimination, 简写为RFE)。它是一种贪婪的优化算法,旨在找到性能最佳的特征子集。它反复创建模型,并在每次迭代时保留最佳特征或剔除最差特征,下一次迭代时,它会使用上一次建模中没有被选中的特征来构建下一个模型,直到所有特征都耗尽为止。然后,它根据自己保留或剔除特征的顺序来对特征进行排名,最终选出一个最佳子集。包装法的效果是所有特征选择方法中最利于提升模型表现的,它可以使用很少的特征达到很优秀的效果。除此之外,在特征数目相同时,包装法和嵌入法的效果能够匹敌,不过它比嵌入法算得更见缓慢,所以也不适用于太大型的数据。相比之下,包装法是最能保证模型效果的特征选择方法。
4. 模块:feature_selection.RFE(estimator, n_features_to_select=None, step=1, verbose=0)
参数estimator是需要填写的实例化后的评估器,n_features_to_select是想要选择的特征个数,step表示每次迭代中希望移除的特征个数。除此之外,RFE类有两个很重要的属性,.support_:返回所有的特征的是否最后被选中的布尔矩阵,以及.ranking_返回特征的按数次迭代中综合重要性的排名。
5.2 以随机森林为例的包装法
fromsklearn.feature_selectionimportRFE
RFC_ = RFC(n_estimators =10,random_state=0)
selector = RFE(RFC_, n_features_to_select=340, step=50).fit(X, y)
cross_val_score(RFC_,X_wrapper,y,cv=5).mean()
#======【TIME WARNING: 15 mins】======#
core = []
foriinrange(1,751,50):X_wrapper = RFE(RFC_,n_features_to_select=i, step=50).fit_transform(X,y) once = cross_val_score(RFC_,X_wrapper,y,cv=5).mean()score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(1,751,50),score)
plt.xticks(range(1,751,50))
plt.show()

注解:明显能够看出,在包装法下面,应用50个特征时,模型的表现就已经达到了90%以上,比嵌入法和过滤法都高效很多。我们可以放大图像,寻找模型变得非常稳定的点来画进一步的学习曲线(就像我们在嵌入法中做的那样)。如果我们此时追求的是最大化降低模型的运行时间,我们甚至可以直接选择50作为特征的数目,这是一个在缩减了94%的特征的基础上,还能保证模型表现在90%以上的特征组合,不可谓不高效。
同时,我们提到过,在特征数目相同时,包装法能够在效果上匹敌嵌入法。试试看如果我们也使用340作为特征数目,运行一下,可以感受一下包装法和嵌入法哪一个的速度更加快。由于包装法效果和嵌入法相差不多,在更小的范围内使用学习曲线,我们也可以将包装法的效果调得很好。
六、总结
经验来说,过滤法更快速,但更粗糙。包装法和嵌入法更精确,比较适合具体到算法去调整,但计算量比较大,运行时间长。当数据量很大的时候,优先使用方差过滤和互信息法调整,再上其他特征选择方法。使用逻辑回归时,优先使用嵌入法。使用支持向量机时,优先使用包装法。迷茫的时候,从过滤法走起,看具体数据具体分析。
相关文章:

机器学习(10)---特征选择
文章目录 一、概述二、Filter过滤法2.1 过滤法说明2.2 方差过滤2.3 方差过滤对模型影响 三、相关性过滤3.1 卡方过滤3.2 F检验3.3 互信息法3.4 过滤法总结 四、Embedded嵌入法4.1 嵌入法说明4.2 以随机森林为例的嵌入法 五、Wrapper包装法5.1 包装法说明5.2 以随机森林为例的包…...

Python之数据库(MYSQL)连接
一)数据库SQL语言基础 MySQL是一个关系型数据库管理系统,由瑞典MySQL AB 公司开发,目前属于 Oracle 旗下产品。MySQL 是最流行的关系型数据库管理系统之一,在 WEB 应用方面,MySQL是最好的 RDBMS (Relational Database…...
【建站教程】使用阿里云服务器怎么搭建网站?
使用阿里云服务器快速搭建网站教程,先为云服务器安装宝塔面板,然后在宝塔面板上新建站点,阿里云服务器网以搭建WordPress网站博客为例,阿小云来详细说下从阿里云服务器CPU内存配置选择、Web环境、域名解析到网站上线全流程&#x…...

【自然语言处理】关系抽取 —— MPDD 讲解
MPDD 论文信息 标题:MPDD: A Multi-Party Dialogue Dataset for Analysis of Emotions and Interpersonal Relationships 作者:Yi-Ting Chen, Hen-Hsen Huang, Hsin-Hsi Chen 期刊:LREC 2020 发布时间与更新时间:2020 主题:自然语言处理、关系抽取、对话场景、情感预测 数…...

深入理解JVM虚拟机第三篇:JVM的指令集架构模型和JVM的生命周期
文章目录 一:JVM的指令集架构模型 1:基于栈式架构的特点...

[小尾巴 UI 组件库] 组件库配置与使用
文章归档于:https://www.yuque.com/u27599042/row3c6 组件库地址 npm:https://www.npmjs.com/package/xwb-ui?activeTabreadme小尾巴 UI 组件库源码 gitee:https://gitee.com/tongchaowei/xwb-ui小尾巴 UI 组件库测试代码 gitee:…...
函数的理解)
Linux系统中fork()函数的理解
fork() 函数是一个在Unix和类Unix操作系统中常见的系统调用,用于创建一个新的进程,该进程是调用进程(父进程)的副本。fork() 函数的工作原理如下: 1. 当父进程调用 fork() 时,操作系统会创建一个新的进程&a…...
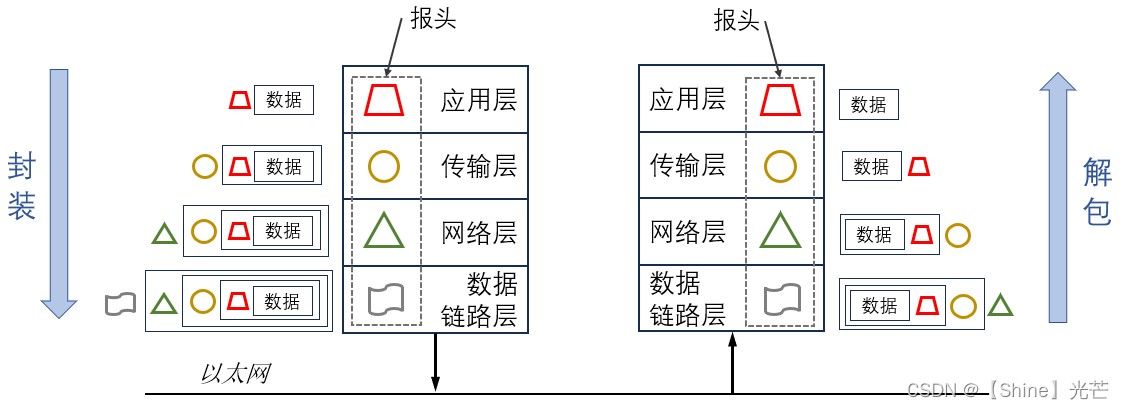
Linux网络编程:网络协议及网络传输的基本流程
目录 一. 计算机网络的发展 二. 网络协议的认识 2.1 对于协议分层的理解 2.2 TCP/IP五层协议模型 2.3 OSI七层模型 三. 网络传输的流程 3.1 同一网段中计算机通信的流程 3.2 不同网段中计算机设备的通信 3.3 对于IP地址和MAC地址的理解 3.4 数据的封装和解包 四. 总结…...

【大数据之Kafka】十、Kafka消费者工作流程
1 Kafka消费方式 (1)pull(拉)模式:消费者从broker中主动拉取数据。(Kafka中使用) 不足:如果Kafka中没有数据,消费者可能会陷入循环,一直返回空数据。 &#…...

如何确保ChatGPT的文本生成对特定行业术语的正确使用?
确保ChatGPT在特定行业术语的正确使用是一个重要而复杂的任务。这涉及到许多方面,包括数据预处理、模型训练、微调、评估和监控。下面我将详细介绍如何确保ChatGPT的文本生成对特定行业术语的正确使用,并探讨这一过程中的关键考虑因素。 ### 1. 数据预处…...
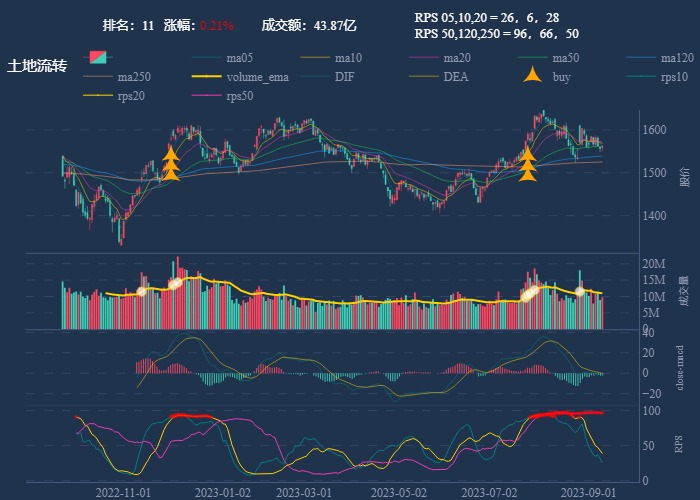
行业追踪,2023-09-11
自动复盘 2023-09-11 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...
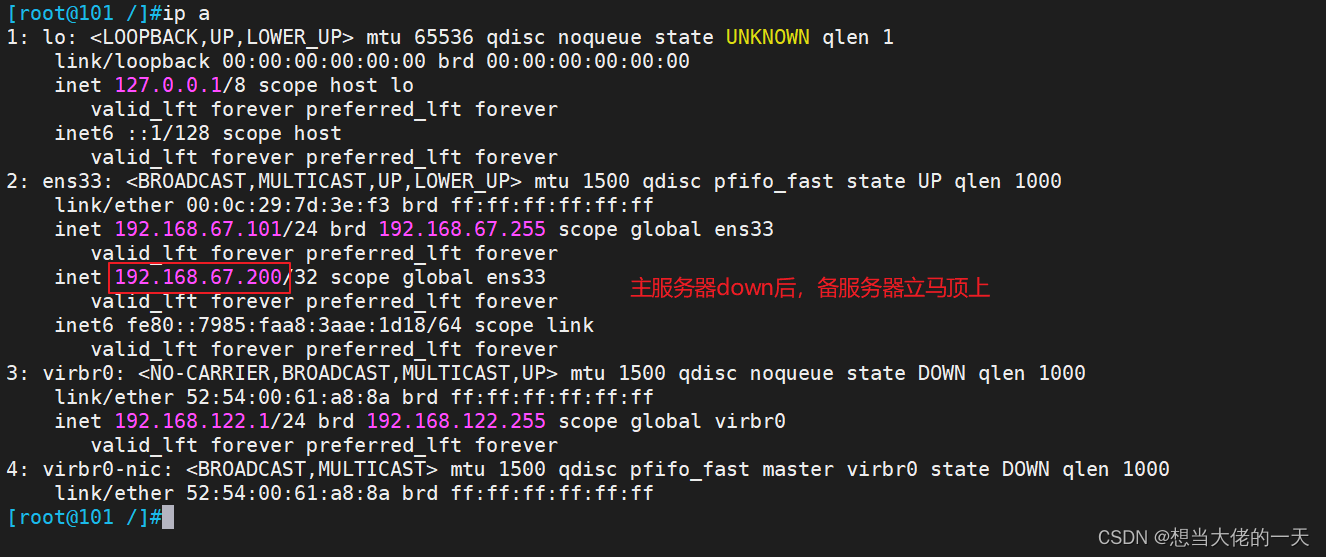
LVS + Keepalived群集
文章目录 1. Keepalived工具概述1.1 什么是Keepalived1.2 工作原理1.3 Keepailved实现原理1.4 Keepalived体系主要模块及其作用1.5 keepalived的抢占与非抢占模式 2. 脑裂现象 (拓展)2.1 什么是脑裂2.2 脑裂的产生原因2.3 如何解决脑裂2.4 如何预防脑裂 …...

springboot将jar改成war
一、maven项目 1、修改pom文件 <packaging>war</packaging>2、添加Servlet API依赖,Spring Boot的Starter依赖通常会包含这个依赖,所以你可能已经有了,没有就需要添加 <dependency><groupId>javax.servlet</gr…...

从9.10拼多多笔试第四题产生的01背包感悟
文章目录 题面基本的01背包问题本题变式 本文参考: 9.10拼多多笔试ak_牛客网 (nowcoder.com) 拼多多 秋招 2023.09.10 编程题目与题解 (xiaohongshu.com) 题面 拼多多9.10笔试的最后一题,是一道比较好的01背包变式问题,可以学习其解法加深对…...
搭建自己的OCR服务,第一步:选择合适的开源OCR项目
一、OCR是什么? 光学字符识别(Optical Character Recognition, OCR)是指对文本资料的图像文件进行分析识别处理,获取文字及版面信息的过程。 亦即将图像中的文字进行识别,并以文本的形式返回。 二、OCR的基本流程 1…...

【C++】VScode配置C/C++语言环境(简洁易懂版)
目录 一、下载VScode(装好直接跳第五步)二、安装VScode三、VScode设置语言为中文四、VScode切换主题(个人爱好)五、下载C语言编译器(MinGW-W64 GCC)六、配置编译器环境变量七、配置VScode八、使用单独窗口…...

【hive】—原有分区表新增加列(alter table xxx add columns (xxx string) cascade;)
项目场景: 需求:需要在之前上线的分区报表中新增加一列。 实现方案: 1、创建分区测试表并插入测试数据 drop table test_1; create table test_1 (id string, score int, name string ) partitioned by (class string) row format delimit…...
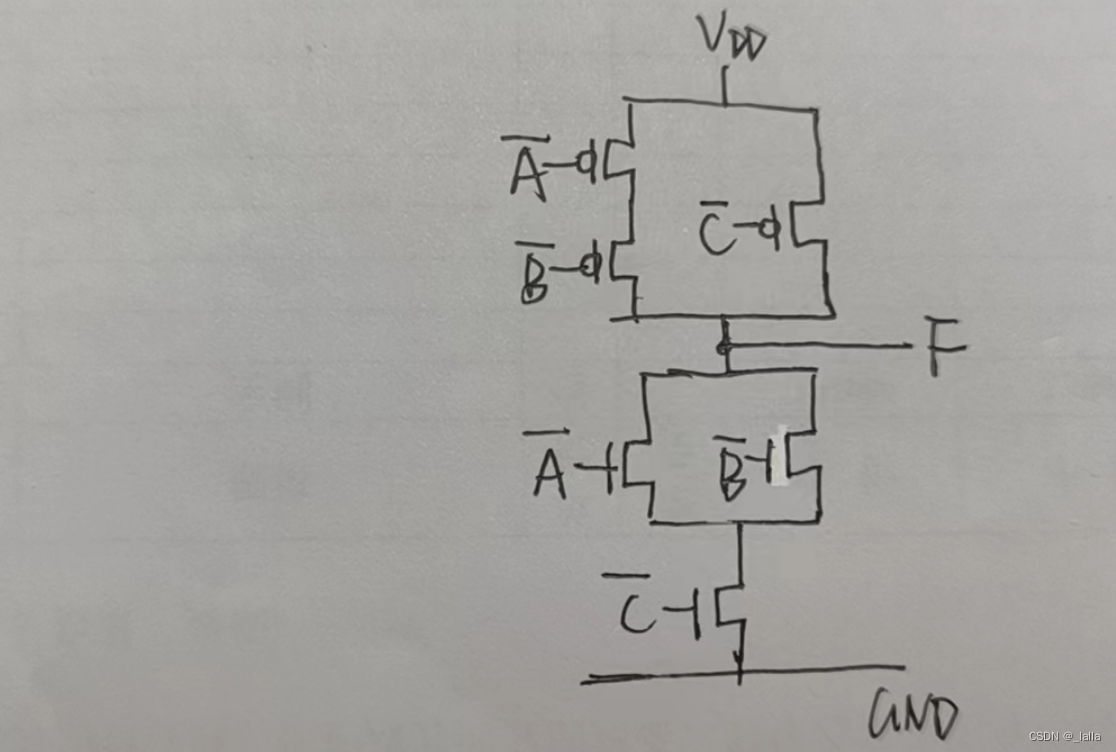
verilog学习笔记7——PMOS和NMOS、TTL电路和CMOS电路
文章目录 前言一、PMOS和NMOS1、NMOS2、PMOS3、增强型和耗尽型4、两者面积大小 二、CMOS门电路1、非门2、与非门3、或非门4、线与逻辑5、CMOS传输门6、三态门 三、TTL电路四、TTL电路 VS CMOS电路五、数字电平六、使用CMOS电路实现逻辑函数1、上拉网络 PUN2、下拉网络 PDN3、实…...

Java知识点二
Java知识点二 1、Comparable内部比较器,Comparator外部比较器2、源码结构的区别:1)Comparable接口:2)Comparator接口: 2、Java反射 1、Comparable内部比较器,Comparator外部比较器 我们一般把Comparable叫…...
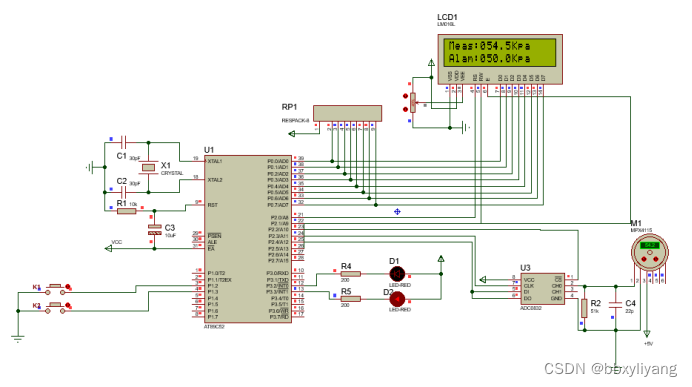
基于单片机压力传感器MPX4115检测-报警系统-proteus仿真-源程序
一、系统方案 本设计采用52单片机作为主控器,液晶1602显示,MPX4115检测压力,按键设置报警,LED报警。 二、硬件设计 原理图如下: 三、单片机软件设计 1、首先是系统初始化 /***************************************…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
