数学建模--退火算法求解最值的Python实现
目录
1.算法流程简介
2.算法核心代码
3.算法效果展示
1.算法流程简介
"""
1.设定退火算法的基础参数
2.设定需要优化的函数,求解该函数的最小值/最大值
3.进行退火过程,随机产生退火解并且纠正,直到冷却
4.绘制可视化图片进行了解退火整体过程
"""2.算法核心代码
#利用退火算法求解函数的极值(优化问题)
import numpy as np
from random import random
import random
import math
import matplotlib.pyplot as plt
#设定退火算法的基础参数
x_min,x_max=(-3,3)#x的取值范围
alpha=0.99#降温系数为0.99
bg_temp=100#起始温度
ed_temp=0.01#最终温度(可设可不设)
cycle_number=500#循环次数
#设定需要优化的函数,求解该函数的最小值
"""
需要运用的化直接修改函数即可.
不过需要注意定义域的问题,主动修改一下定义域就行
"""
def opt_fun(x):y=11*np.sin(2*x)+7*np.cos(5*x)return y
#由于没有具体的数据,我们直接随机设置值就行随机产生初始值#随机产生本次退火解
def new_result(x):x1=x+bg_temp*random.uniform(-1,1)#退火解的合理性检查并且纠正:if x_min<=x1<=x_max:return x1elif x1<x_min:add_min=random.uniform(-1,1)return add_min*x_min+(1-add_min)*xelse:add_max=random.uniform(-1,1)return add_max*x_max+(1-add_max)*x
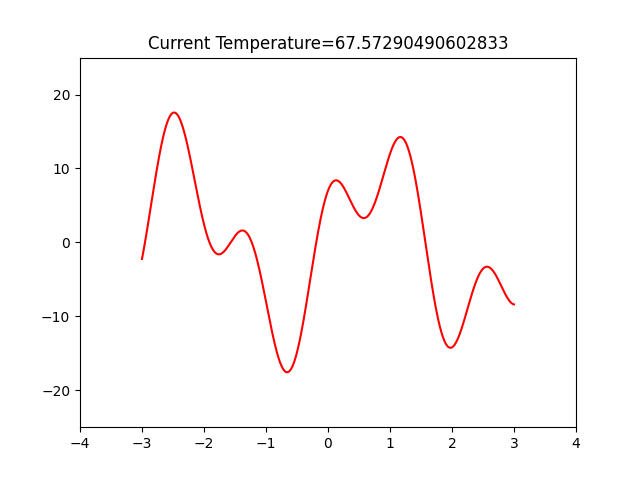
def draw_picture(x):plt.cla()#绘图的时候这里可以进行修改#注意这里y的取值范围[-25,25]要大体预估一下plt.axis([x_min-1,x_max+1,-25,25])m=np.arange(x_min,x_max,0.0001)plt.plot(m,opt_fun(m),color='red')plt.plot(x,opt_fun(x),marker='*',color='b',markersize='8')plt.title('Current Temperature={}'.format(T))plt.pause(0.1)#设定接受概率函数
def p(x,x1):return math.exp(-abs(opt_fun(x)-opt_fun(x1))/T)#循环退火过程,直到冷却求出最优解
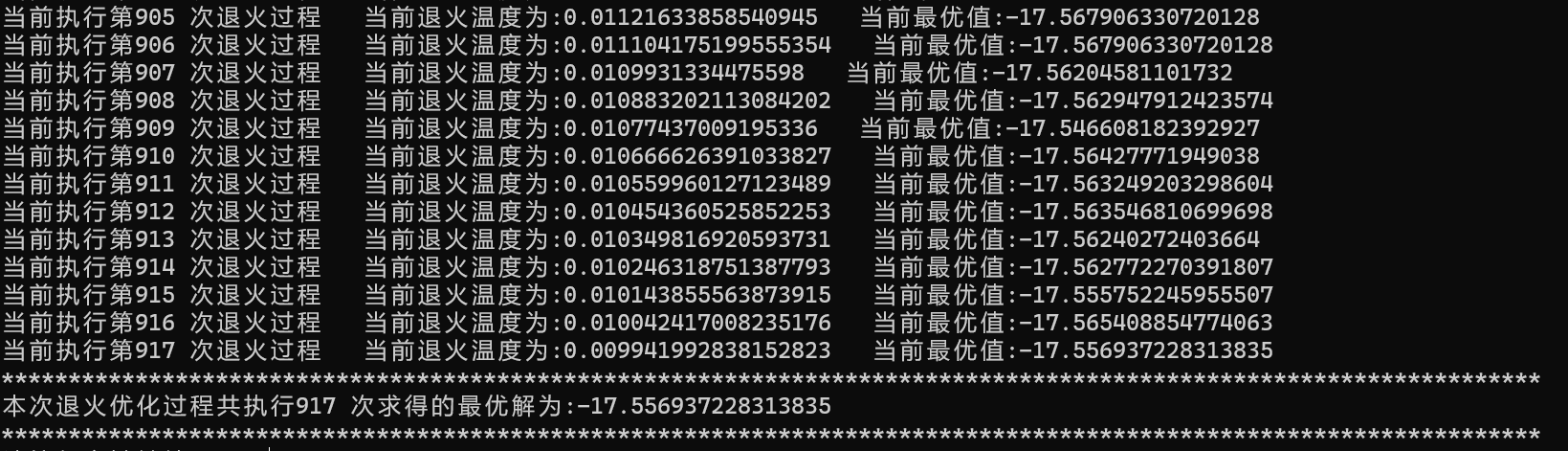
def Annealing_cycle():global Tcount_number=0T=bg_tempx=random.uniform(x_min,x_max)print("*******************************************************************************************************************")while T>ed_temp:draw_picture(x)for i in range(cycle_number):x1=new_result(x)#求解最小值的过程if opt_fun(x)>=opt_fun(x1):x=x1else:if random.random()<=p(x,x1):x=x1else:continueT=T*alphacount_number=count_number+1print("当前执行第{}".format(count_number),"次退火过程"," 当前退火温度为:{}".format(T)," 当前最优值:{}".format(opt_fun(x)))print("*******************************************************************************************************************")print("本次退火优化过程共执行{}".format(count_number),"次求得的最优解为:{}".format(opt_fun(x)))print("*******************************************************************************************************************")
Annealing_cycle()3.算法效果展示
相关文章:
数学建模--退火算法求解最值的Python实现
目录 1.算法流程简介 2.算法核心代码 3.算法效果展示 1.算法流程简介 """ 1.设定退火算法的基础参数 2.设定需要优化的函数,求解该函数的最小值/最大值 3.进行退火过程,随机产生退火解并且纠正,直到冷却 4.绘制可视化图片进行了解退火整体过程 &…...

地理地形sdk:Tatuk GIS Developer Kernel for .NET Crack
Tatuk GIS Developer Kernel for .NET 是一个变体,它是受控代码和 .NET GIS SDK,用于为用户 Windows 操作系统创建专业 GIS 软件的过程。它被认为是一个完全针对Win Forms 的.NET CIL,WPF 框架是针对C# 以及VB.NET、VC、Oxy 以及最终与.NET 的…...
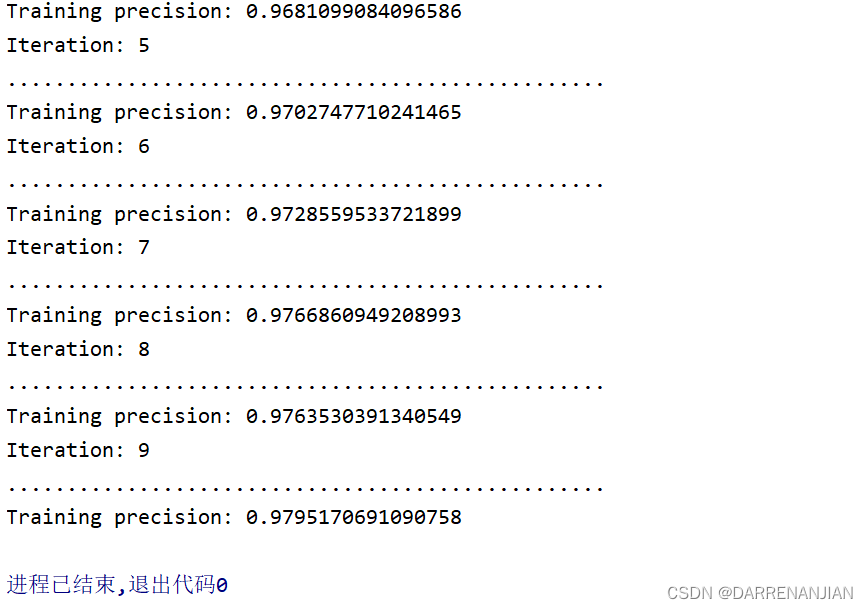
Day_81-87 CNN卷积神经网络
目录 一. CNN卷积神经网络与传统神经网络的不同 1. 模型图 2. 参数分布情况 3. 卷积神经网络和传统神经网络的层次结构 4. 传统神经网络的缺点: 二. CNN的基本操作 1. 卷积 2. 池化 三. CNN实现过程 1. 算法流程图 2. 输入层 3. 卷积层 4. 激活层 5. 池化层 6. 全连…...

关于mybatisplus报错:Property ‘sqlSessionFactory‘ or ‘sqlSessionTemplat的问题
可能是mybatisplus版本不兼容的问题,我之前用的3.4.0,springboot版本是3.1.3,maven版本是3.8.8,运行的时候报了这个错。现在修改了mybatisplus的版本,如下图: 这样就不报错了。 大家可以在这里找合适的my…...

Spring AOP基础动态代理基于JDK动态代理实现
目录 1. 预备知识-动态代理 1.1 什么是动态代理 1.2 动态代理的优势 1.3 基于JDK动态代理实现 2. AOP 2.1 基本概念 2.2 AOP带来的好处 3. Spring AOP 3.1 前置通知 3.2 后置通知 3.3 环绕通知 3.4 异常通知 3.5 适配器 1. 预备知识-动态代理 1.1 什么是动态代理…...

第一章 计算机系统概述 五、中断和异常、系统调用
目录 一、中断的作用 二、中断的类型 1、内中断(异常) 2、外中断 三、中断机制的基本原理 四、系统调用 1、定义: 2、与库函数的区别 3、按功能分类 4、作用 一、中断的作用 1、“中断”是让操作系统内核夺回CPU使用权的唯一途径 …...

【C语言】文件操作(上)
一.什么是文件 文件是磁盘上的文件,文件中存放的数据不随程序的退出而销毁. 二.文件的打开与关闭 1.文件指针 每个被使用的文件都在内存中开辟了一个相应的文件信息区,用来存放文件的相关信息(如文件的名字,文件状态及文件当前的位置等&…...
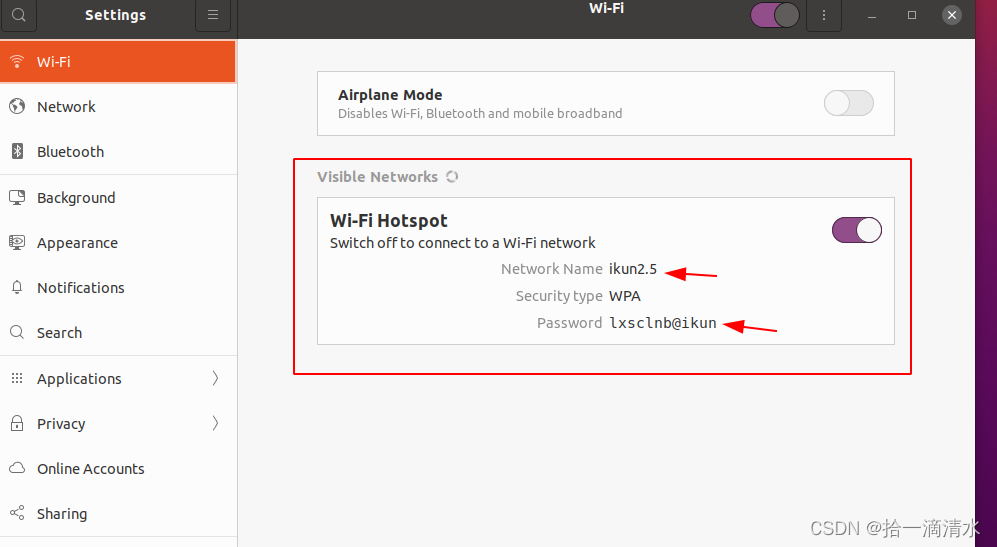
【Linux】让笔记本发挥余热,Ubuntu20.04设置WiFi热点
Ubuntu20.04设置WiFi热点 由于卧室距离客厅较远,wifi信号太弱,体验极差。鉴于卧室的笔记本电脑是通过网线连接的客厅路由器,因此考虑将这台老破笔记本作为“路由器”,以便发挥它的余热。实验证明,上网速度提升数十倍&a…...

【云平台】遥感地信云平台收录
文章目录 国内1 航天宏图PIE-Engine2 商汤科技3 AI Earth4 EarthDataMiner国外结语国内 1 航天宏图PIE-Engine https://engine.piesat.cn/live-show-list 在这里插入图片描述 2 商汤科技 https://senseearth-cloud.com/map 3 AI Earth https://engine-aiearth.aliyun.com…...

23种设计模式之---单例模式
闲来无事学一下设计模式,希望这23种可以一直更下去,什么时候能更完呢,也许一个月,也许一年,也许断更 设计模式六大原则 本文是23篇的第一篇,在学习设计模式之前,你需要了解下六大原则。 1、开…...
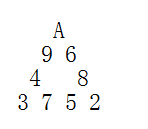
蓝桥杯官网练习题(纸牌三角形)
题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 A,2,3,4,5,6,7,8,9 共 99 张纸牌排成一个正三角形(A 按 1 计算)。要求每个边的和相等。 下图就是一种排法。 这样的排法可能会有很多。 如果…...

一辆新能源汽车的诞生之旅:比亚迪常州工厂探营
作为在新能源汽车领域首屈一指的国产品牌,比亚迪近年来可以说是捷报频传,高奏凯歌。 以比亚迪常州工厂为例,据介绍该工厂当初规划设计时定下的生产目标,是年产量能够达到20万辆。然而在2023年上半年,该工厂光是主要销往…...

【算法专题突破】双指针 - 最大连续1的个数 III(11)
目录 1. 题目解析 2. 算法原理 3. 代码编写 写在最后: 1. 题目解析 题目链接:1004. 最大连续1的个数 III - 力扣(Leetcode) 这道题不难理解,其实就是求出最长的连续是1的子数组, 但是,他支…...

java实现备忘录模式
备忘录模式是一种行为设计模式,它允许您捕获一个对象的内部状态,并在稍后的时间点将其恢复。这对于需要撤销操作或恢复到先前状态的应用程序非常有用。以下是在 Java 中实现备忘录模式的一般步骤: 创建一个原发器类(Originator&am…...
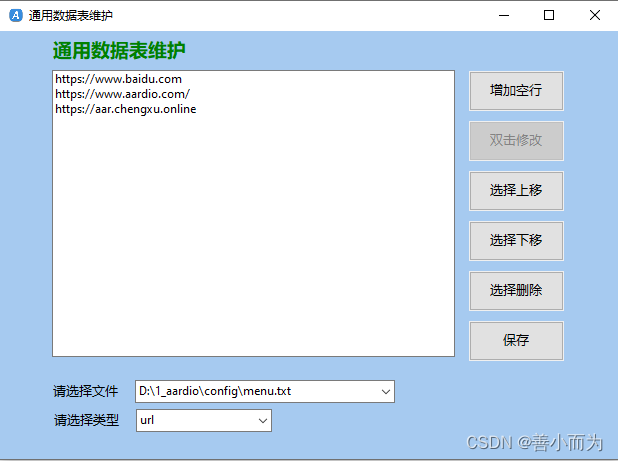
aardio语言的通用数据表维护
import win.ui; /*DSG{{*/ var winform win.form(text"通用数据表维护";right617;bottom427;bgcolor15780518) winform.add( buttonAdd{cls"button";text"增加空行";left469;top40;right564;bottom80;flat1;z2}; buttonDel{cls"button&quo…...

手写RPC框架--7.封装响应
RPC框架-Gitee代码(麻烦点个Starred, 支持一下吧) RPC框架-GitHub代码(麻烦点个Starred, 支持一下吧) 封装响应 封装响应a.封装响应b.请求id生成器(雪花算法)c.抽象序列化d.建立序列化工厂e.hessian的序列化方式(拓展) 封装响应 a.封装响应 在core模块…...
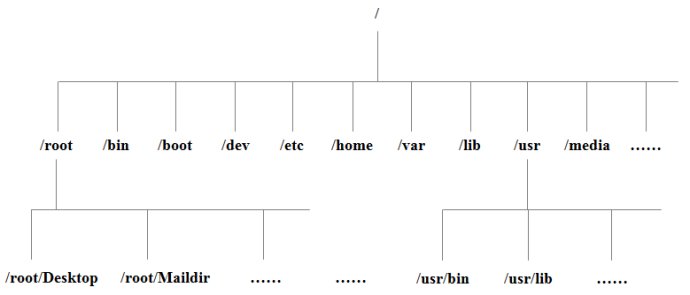
Linux入门教程||Linux系统目录结构
登录系统后,在当前命令窗口下输入命令: ls / 你会看到如下图所示: 树状目录结构: 以下是对这些目录的解释: /bin: bin是Binary的缩写, 这个目录存放着最经常使用的命令。 /boot: 这里存放的是启动Linux时…...

LeetCode 88. 合并两个有序数组
文章目录 一、题目二、C# 题解 一、题目 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 注意&a…...
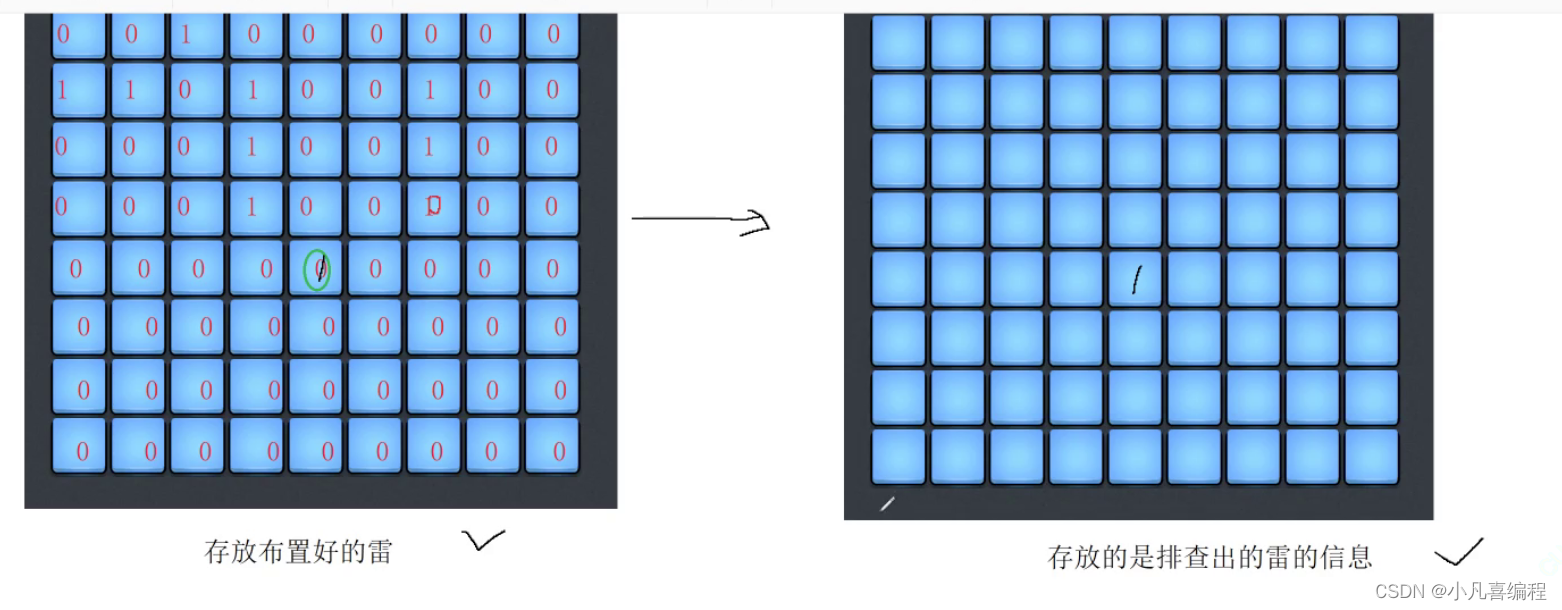
C语言实现扫雷小游戏
1.首先扫雷游戏要存储布置好的雷信息,需要一个二维数组 不是雷放* 雷:# 不是雷:0 雷:1 2. 给2个二维数组 9*9 一个存放雷的信息,一个存放布置好雷的信息 3.为了防止在统计坐标周围的…...
【linux基础(五)】Linux中的开发工具(上)---yum和vim
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:Linux从入门到开通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学更多操作系统知识 🔝🔝 Linux中的开发工具 1. 前言2.…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
