LeetCode 1359. Count All Valid Pickup and Delivery Options【动态规划,组合数学】1722
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

给你 n 笔订单,每笔订单都需要快递服务。
请你统计所有有效的 收件/配送 序列的数目,确保第 i 个物品的配送服务 delivery(i) 总是在其收件服务 pickup(i) 之后。
由于答案可能很大,请返回答案对 10^9 + 7 取余的结果。
示例 1:
输入:n = 1
输出:1
解释:只有一种序列 (P1, D1),物品 1 的配送服务(D1)在物品 1 的收件服务(P1)后。
示例 2:
输入:n = 2
输出:6
解释:所有可能的序列包括:
(P1,P2,D1,D2),(P1,P2,D2,D1),(P1,D1,P2,D2),(P2,P1,D1,D2),(P2,P1,D2,D1) 和 (P2,D2,P1,D1)。
(P1,D2,P2,D1) 是一个无效的序列,因为物品 2 的收件服务(P2)不应在物品 2 的配送服务(D2)之后。
示例 3:
输入:n = 3
输出:90
提示:
1 <= n <= 500
解法 动态规划+组合数学+递推
设 f [ i ] f[i] f[i] 表示订单数量为 i 时的序列数目,我们希望通过 f [ 1 ] , f [ 2 ] , . . . , f [ i − 1 ] f[1], f[2], ..., f[i - 1] f[1],f[2],...,f[i−1] 得到 f [ i ] f[i] f[i] 的值,这样就可以使用递推的方法得到 f [ n ] f[n] f[n] 了。
由于 f [ i ] f[i] f[i] 包含了 i i i 份订单,我们可以将其拆分为前 i − 1 i - 1 i−1 份订单(编号为 1 , 2 , . . . , i − 1 1, 2, ..., i - 1 1,2,...,i−1 )与 1 1 1 份额外的订单(编号为 i)。对于一个包含前 i − 1 i - 1 i−1 份订单的固定序列,它的长度为 ( i − 1 ) ∗ 2 (i - 1) * 2 (i−1)∗2 ,我们只需要在这个序列中加上第 i i i 份订单,就可以得到一条订单数量为 i i i 的序列。
那么有多少种不同的方法能够加上第 i i i 份订单呢?第 i 份订单包含 P i P_i Pi 和 D i D_i Di ,并且 P i P_i Pi 在序列中必须出现在 D i D_i Di 之前,那么我们可以将这些方法分成两类:
- 第一类: P i P_i Pi 和 D i D_i Di 被添加到了序列中连续的位置。由于序列的长度为 ( i − 1 ) ∗ 2 (i - 1) * 2 (i−1)∗2 ,那么可以添加的位置为序列的长度加 1 1 1 ,即 2 ( i − 1 ) + 1 = 2 i − 1 2(i - 1) + 1 = 2i - 1 2(i−1)+1=2i−1 ;
- 第二类: P i P_i Pi 和 D i D_i Di 被添加到了序列中不连续的位置,那么就相当于在 i ∗ 2 − 1 i * 2 - 1 i∗2−1 个位置中选择两个不同的位置,前者用作添加 P i P_i Pi ,后者用作添加 D i D_i Di ,方法数为组合数 ( 2 i − 1 2 ) = ( 2 i − 1 ) ( i − 1 ) \binom{2i - 1}{2} = (2i - 1)(i - 1) (22i−1)=(2i−1)(i−1) 。
将这两类的方法数量相加,就可以得到:对于一个固定的包含前 i − 1 i - 1 i−1 份订单的固定序列,用 ( 2 i − 1 ) i (2i-1)i (2i−1)i 种方法可以加入第 i i i 份订单。由于前 i − 1 i - 1 i−1 份订单对应的序列数目为 f [ i − 1 ] f[i - 1] f[i−1] ,并且对于任意两个不同的包含前 i − 1 i - 1 i−1 份订单的序列,都不会因为加上第 i i i 份订单使得它们变得相同。因此我们就得到了递推公式:
f [ i ] = ( 2 i − 1 ) i ∗ f [ i − 1 ] f[i] =(2i−1)i∗f[i−1] f[i]=(2i−1)i∗f[i−1]
由于递推公式中 f [ i ] f[i] f[i] 仅与 f [ i − 1 ] f[i - 1] f[i−1] 有关,我们在递推式可以只存储 f [ i − 1 ] f[i - 1] f[i−1] 的值,而不用把 f [ 1 ] , f [ 2 ] , . . . , f [ i − 1 ] f[1], f[2], ..., f[i - 1] f[1],f[2],...,f[i−1] 都记录下来。
using LL = long long;class Solution {
private:static constexpr int mod = 1000000007;
public:int countOrders(int n) {if (n == 1) return 1;int ans = 1;for (int i = 2; i <= n; ++i)ans = (LL)ans * (i * 2 - 1) % mod * i % mod;return ans;}
};
复杂度分析:
- 时间复杂度: O ( N ) O(N) O(N) 。
- 空间复杂度: O ( 1 ) O(1) O(1) 。
解法2 整体法
除了递推法之外,我们也可以从整体进行考虑,直接得到 f [ i ] f[i] f[i] 的通项公式。
假设现在没有 D i D_i Di 必须在 P i P_i Pi 之后的要求,那么
f [ i ] = ( 2 i ) ! f[i] =(2i)! f[i]=(2i)!
这是因为我们可以将 P 1 , D 1 , P 2 , D 2 , ⋯ , P i , D i P_1, D_1, P_2, D_2, \cdots, P_i, D_i P1,D1,P2,D2,⋯,Pi,Di 的任意一个排列作为答案,排列的数目为 ( 2 i ) ! (2i)! (2i)! 。我们称这些排列为初始排列。
那么在加上了「 D i D_i Di 必须在 P i P_i Pi 之后」的要求后,有一些初始排列就不能作为答案了。但是我们可以对它们进行调整,使它们变成满足要求的排列。具体地,对于任意一个初始排列,如果第 j j j 个物品的 D j D_j Dj 出现在 P j P_j Pj 之前,那么我们就把 D j D_j Dj 和 P j P_j Pj 交换顺序。在对 j = 1 , 2 , . . . , i j = 1, 2, ..., i j=1,2,...,i 全部判断一遍之后,我们就可以得到一个满足要求的排列了。然而这样会导致重复计数,这是因为不同的初始排列在交换顺序之后会得到相同的排列,例如当 i = 2 i = 2 i=2 时,初始排列
D 1 , D 2 , P 1 , P 2 D 1 , P 2 , P 1 , D 2 \begin{aligned}D1, D2, P1, P2 \\ D1, P2, P1, D2\end{aligned} D1,D2,P1,P2D1,P2,P1,D2
在交换后都会得到相同的排列 P 1 , P 2 , D 1 , D 2 P1, P2, D1, D2 P1,P2,D1,D2 如何去除重复计数呢?我们可以进行逆向思考,反过来计算一个排列可以从多少个初始排列得来。显然,对于排列中的 i i i 对 P j P_j Pj 和 D j D_j Dj ,我们将其中任意数量的对交换顺序,都可以得到一个不同的初始排列。交换顺序的选择有 2 i 2^i 2i 种(每一对 P j P_j Pj 和 D j D_j Dj 交换或不交换),因此一个排列对应着 2 i 2^i 2i 个初始排列,即排列的数目为:
f [ i ] = ( 2 i ) ! 2 i f[i] = \frac{(2i)!}{2^i} f[i]=2i(2i)!
这样就得到了 f [ i ] f[i] f[i] 的通项公式。由于通项公式中包含除法,在取模的意义下不好直接计算,我们可以将分母 2 i 2^i 2i 拆分成 i i i 个 222,与分子阶乘中的 i i i 个偶数相除,得到
f [ i ] = i ! ( 2 i − 1 ) ! ! f[i] = i!(2i-1)!! f[i]=i!(2i−1)!!
其中 ( 2 i − 1 ) ! ! = 1 ⋅ 3 ⋅ ⋯ ⋅ ( 2 i − 1 ) (2i-1)!! = 1 \cdot 3 \cdot \cdots \cdot (2i-1) (2i−1)!!=1⋅3⋅⋯⋅(2i−1) ,其与方法一中的递推式是一致的,可以直接使用方法一的代码。
相关文章:

LeetCode 1359. Count All Valid Pickup and Delivery Options【动态规划,组合数学】1722
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

[杂谈]-从硬件角度理解二进制数
从硬件角度理解二进制数 文章目录 从硬件角度理解二进制数1、概述2、模拟电路3、数字电路4、逻辑电平5、TTL 器件的电压水平6、总结 1、概述 二进制数以 2 为基数系统表示,该系统只有两 (2) 个不同的数值,即 0 和 1。就像最常见的那样,十进制…...
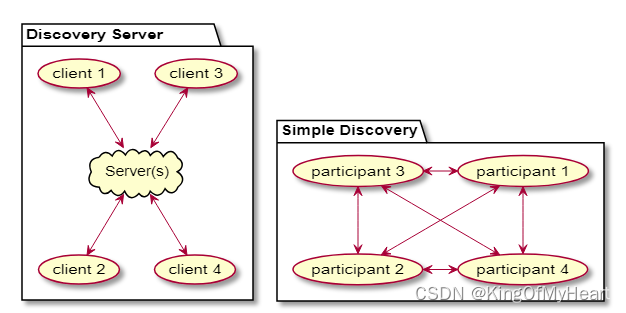
Fast-DDS 服务发现简要概述
阅读本文章需要对DDS基础概念有一些了解,一些内容来自Fast-DDS官方文档,一些是工作中踩过的坑。 1. 服务发现阶段 满足OMG标准的DDS服务发现分为两部分,分别是: PDP(Participant Discovery Protocol 参与者发现协议):参与者确认…...
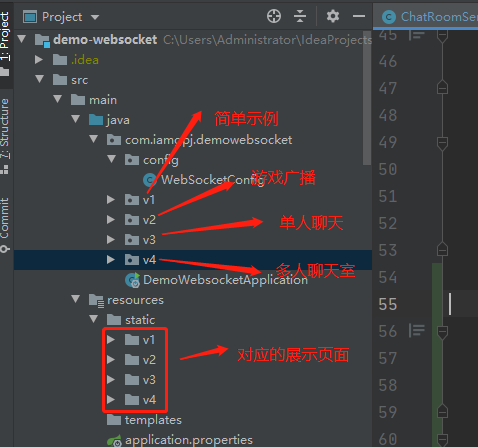
基于spingboot的websocket订阅、广播、多人聊天室示例
概述 基于spingboot的websocket多人聊天系统。包括订阅,广播、点对点单人聊天,多人聊天室功能。 详细 一、运行效果 简单示例 广播 单人聊天 多人聊天室 二、相关代码 websocket配置 package com.iamgpj.demowebsocket.config;import com.iamgpj.d…...
Linux mac Windows三系统 局域网文件共享方法
主要工具: Samba是一个开源的软件套件,允许Linux系统与Windows系统之间共享文件和打印机。 一、首先是Linux共享的设置 ①安装 sudo apt-get install samba ②创建共享文件夹 sudo mkdir /home/share ③配置用户 sudo smbpasswd -a kequan ④修改…...
Java——比较器
引入的背景 我们知道基本数据类型的数据(除boolean类型外)需要比较大小的话,直接使用比较运算符即可,但是引用数据类型是不能直接使用比较运算符来比较大小的。那么,如何解决这个问题呢? 在Java中经常会涉…...

【数据结构】初识泛型
文章目录 一般的类和方法,只能使用具体的类型: 要么是基本类型,要么是自定义的类。这种限制对代码的束缚就会很大。所以我们引入了泛型。泛型,泛顾名思义就是广泛的意思。就是适用于许多许多类型。从代码上讲,就是对类型实现了参数…...

代码随想录--哈希--有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。 示例 1: 输入: s "anagram", t "nagaram" 输出: true 示例 2: 输入: s "rat", t "car" 输出: false 说明: 你可以假设字符串只包含小写字母。…...

MySQL——数据的增删改
2023.9.12 本章开始学习DML (数据操纵语言) 语言。相关学习笔记如下: #DML语言 /* 数据操作语言: 插入:insert 修改:update 删除:delete */#一、插入语句 #方式一:经典的插入 /* 语法: insert …...

云服务器与http服务器
如何与http服务器建立连接(客户端)? http请求设计格式: 例子: 发送http请求 http数据响应格式: 接收http服务器返回的数据需要进一步进行字符串处理操作,提取有用的数据。...
golang教程 beego框架笔记一
安装beego 安装bee工具 beego文档 # windos 推荐使用 go install github.com/beego/bee/v2master go get -u github.com/beego/bee/v2masterwindows使用安装bee工具时碰到的问题; 环境配置都没有问题,但是执行官网的命令:go get -u github…...
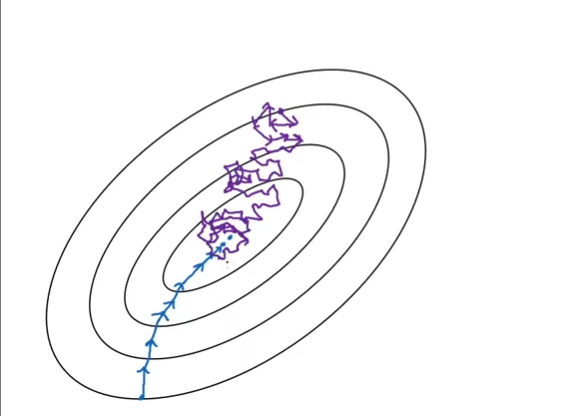
【深度学习】Mini-Batch梯度下降法
Mini-Batch梯度下降法 在开始Mini-Batch算法开始之前,请确保你已经掌握梯度下降的最优化算法。 在训练神经网络时,使用向量化是加速训练速度的一个重要手段,它可以避免使用显式的for循环,并且调用经过大量优化的矩阵计算函数库。…...

AI项目六:WEB端部署YOLOv5
若该文为原创文章,转载请注明原文出处。 一、介绍 最近接触网页大屏,所以就想把YOLOV5部署到WEB端,通过了解,知道了两个方法: 1、基于Flask部署YOLOv5目标检测模型。 2、基于Streamlit部署YOLOv5目标检测。 代码在…...

敲代码常用快捷键
1、代码拖动 PyCharm:按住 shiftalt鼠标选中某一区域来拖动,即可实现拖动这一区域至指定区域。Visual Studio Code (VSCode): - Windows/Linux:Alt 鼠标左键拖动 - MacOS:Option 鼠标左键拖动 IntelliJ IDEA: - Win…...

MyBatis: 分页插件PageHelper直接传递分页参数的用法
一、加分页插件依赖 <dependency><groupId>com.github.pagehelper</groupId><artifactId>pagehelper-spring-boot-starter</artifactId><version>1.2.13</version></dependency>二、配置分页插件,并配置相关属性&a…...
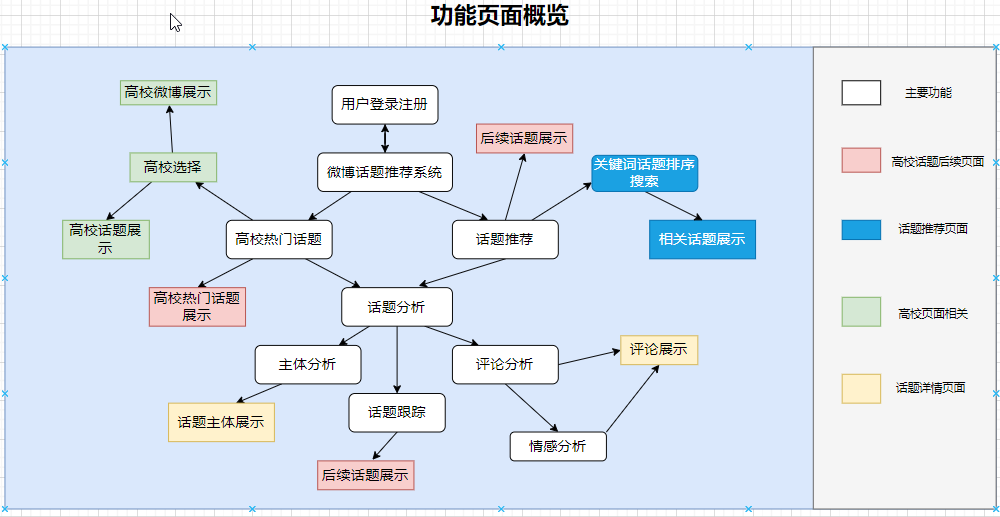
Python基于Flask的高校舆情分析,舆情监控可视化系统
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W,Csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 运行效果图 基于Python的微博大数据舆情分析,舆论情感分析可视化系统 系统介绍 微博舆情分析系…...

Python第一次作业练习
题目分析: """ 参考学校的相关规定。 对于四分制,百分制中的90分及以上可视为绩点中的4分,80 分及以上为3分,70 分以上为2分,60 分以上为1分; 五分制中的5分为四分制中的4分,4分为3分&#…...

InstallShield打包升级时不覆盖原有文件的解决方案
一个.NET Framework的Devexpress UI Windows Form项目,用的InstallShield,前些个版本都好好的,最近几个版本突然就没法更新了,每次更新的时候都覆盖不了原文件,而且这样更新后第一次打开程序(虽然是老程序&…...

服务器巡检表-监控指标
1、巡检指标 系统资源K8S集群NginxJAVA应用RabbitMQRedisPostgreSQLElasticsearchELK日志系统 2、巡检项 检查项目 检查指标 检查标准 系统资源 CPU 使用率 正常:<70% 低风险:≥ 70% 中风险:≥ 85% 高风险:≥ 9…...

无涯教程-JavaScript - DDB函数
描述 DDB函数使用双倍余额递减法或您指定的某些其他方法返回指定期间内资产的折旧。 语法 DDB (cost, salvage, life, period, [factor])争论 Argument描述Required/OptionalCostThe initial cost of the asset.RequiredSalvage 折旧结束时的价值(有时称为资产的残值)。 该…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
