【C++】AVL树的插入操作实现以及验证是否正确(带平衡因子)
文章目录
- 前言
- 一、AVL树结点的定义
- 二、AVL树的插入(Insert)
- 插入完整代码:
- 1.左单旋(RotateL)
- 2.右单旋(RotateR)
- 3.先右单旋再左单旋(RotateRL)
- 1.保存的bf为0
- 2.保存的bf为1
- 3.保存的bf为-1
- 4.先左单旋再右单旋(RotateLR)
- 三、AVL树的验证
前言
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
1.它的左右子树都是AVL树
2.左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在 O ( l o g 2 n ) O(log_2 n) O(log2n),搜索时间复杂度O( l o g 2 n log_2 n log2n)。
一、AVL树结点的定义
template<class K,class V>
//我们这里用键值的数据类型来举例
struct AVLTreeNode {pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;//(父结点)int _bf;//(平衡因子大小)AVLTreeNode(const pair<K, V>& kv)//构造函数:_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};
二、AVL树的插入(Insert)
AVL树的插入过程可以分为两步:
- 按照二叉搜索树的方式插入新节点
- 调整节点的平衡因子

插入完整代码:
typedef AVLTreeNode<K, V> Node;
bool Insert(const pair<K, V>& kv) {if (_root == nullptr) {//若为空树就先建立结点_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur) {//寻找要插入结点的父亲的位置if (cur->_kv.first < kv.first) {parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first) {parent = cur;cur = cur->_left;}else {return false;}}cur = new Node(kv);//找到要插入结点父亲后,寻找插入其左边还是右边if (parent->_kv.first < kv.first) {parent->_right = cur;}else {parent->_left = cur;}cur->_parent = parent;while (parent) {//更新平衡因子if (parent->_left == cur) {parent->_bf--;}else {parent->_bf ++ ;}// 更新后检测双亲的平衡因子if (parent->_bf == 0) {break;}else if (parent->_bf == 1 || parent->_bf == -1) {// 插入前双亲的平衡因子是0,插入后双亲的平衡因为为1 或者 -1 ,说明以双亲//为根的二叉树的高度增加了一层,因此需要继续向上调整cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2) {// 双亲的平衡因子为正负2,违反了AVL树的平衡性,需要对以parent// 为根的树进行旋转处理if (parent->_bf == 2 && cur->_bf == 1) {RotateL(parent);//左单旋}else if (parent->_bf == -2 && cur->_bf == -1) {RotateR(parent);//右单旋}else if (parent->_bf == 2 && cur->_bf == -1) {RotateRL(parent);//双旋}else if (parent->_bf == -2 && cur->_bf == 1) {RotateLR(parent);//双旋}break;}else {assert(false);}}return true;}
1.左单旋(RotateL)
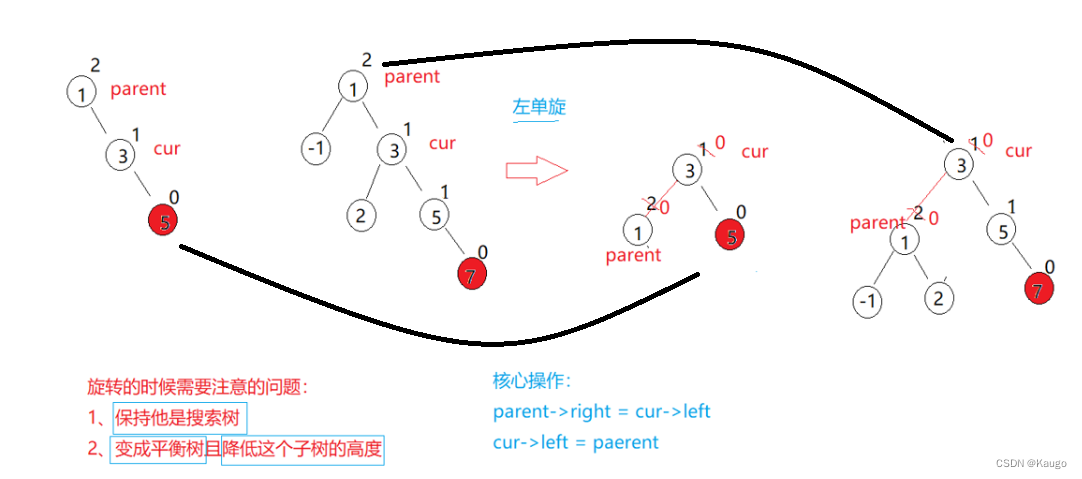
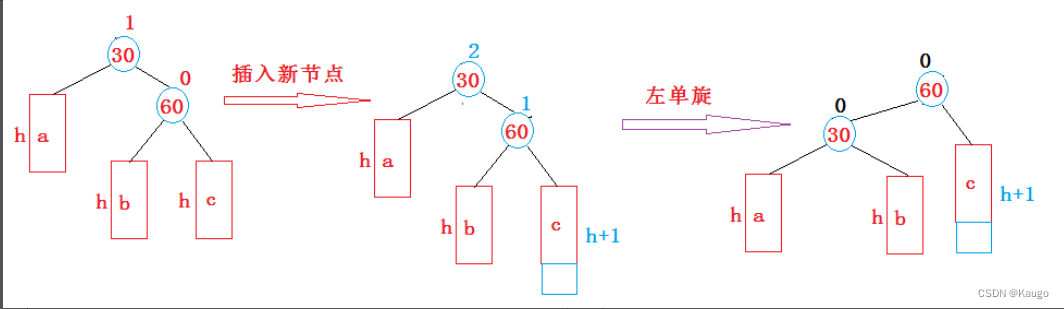
void RotateL(Node* parent) {Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;// 核心操作if (curleft) {//因为curleft可能为空curleft->_parent = parent;}Node* ppnode = parent->_parent;//提前记录下父结点的父亲cur->_left = parent;// 核心操作parent->_parent = cur;if (ppnode == nullptr) {//判断原先parent是否为根节点//因为根节点的父亲为空_root = cur;cur->_parent = nullptr;}else {//说明parent不为根节点//parent可能为ppnode的左或者右子树,改变ppnode的指向if (ppnode->_left == parent) {ppnode->_left = cur;}else {ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;// 根据调整后的结构更新部分节点的平衡因子}
2.右单旋(RotateR)
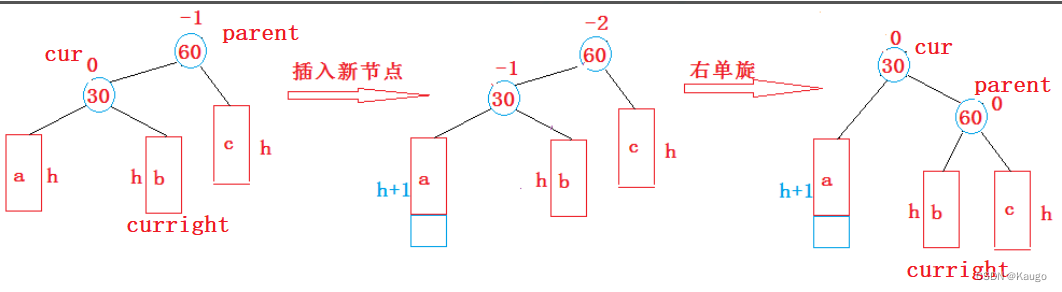
void RotateR(Node* parent) {Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright) {//因为curleft可能为空curright->_parent = parent;}cur->_right = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (ppnode == nullptr) {//判断原先parent是否为根节点//因为根节点的父亲为空_root = cur;cur->_parent = nullptr;}else {//说明parent不为根节点//parent可能为ppnode的左或者右子树,改变ppnode的指向if (ppnode->_left == parent) {ppnode->_left = cur;}else {ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;// 根据调整后的结构更新部分节点的平衡因子}
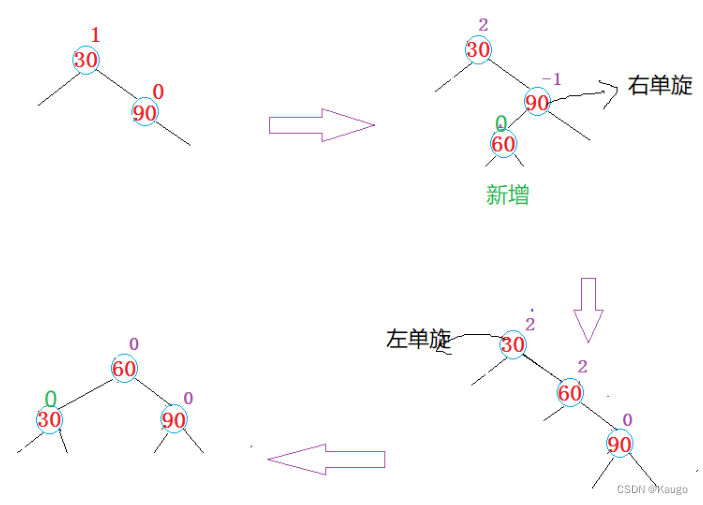
3.先右单旋再左单旋(RotateRL)
以cur为旋转点进行右旋,以parent为旋转点进行左旋,之后进行平衡因子的修改
void RotateRL(Node* parent) {Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;// 旋转之前,保存curleft的平衡因子,旋转完成之后,需要根据该平衡因子来调整其他节//点的平衡因子RotateR(cur);RotateL(parent);if (bf == 0) {cur->_bf = 0;curleft->_bf = 0;parent->_bf = 0;}else if (bf == 1) {cur->_bf = 0;curleft->_bf = 0;parent->_bf = -1;}else if (bf == -1){cur->_bf = 1;curleft->_bf = 0;parent->_bf = 0;}else{assert(false);}}
1.保存的bf为0
2.保存的bf为1
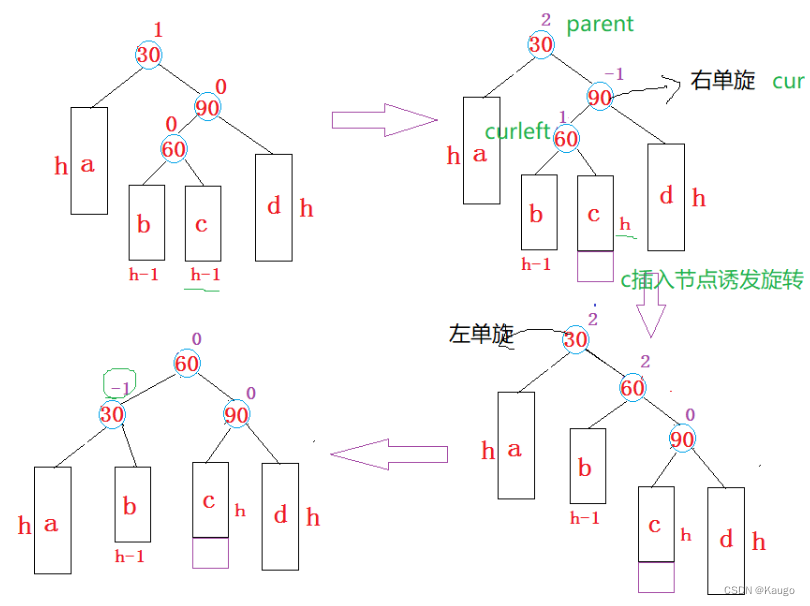
3.保存的bf为-1
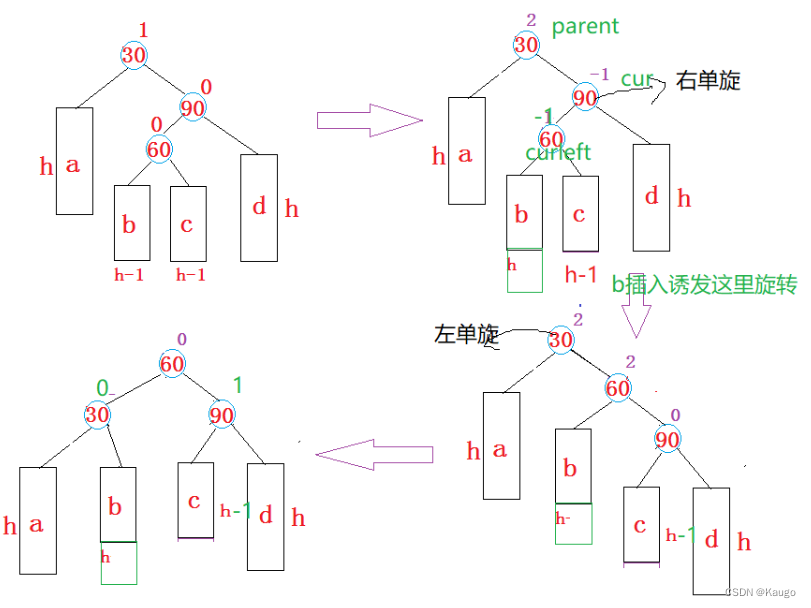
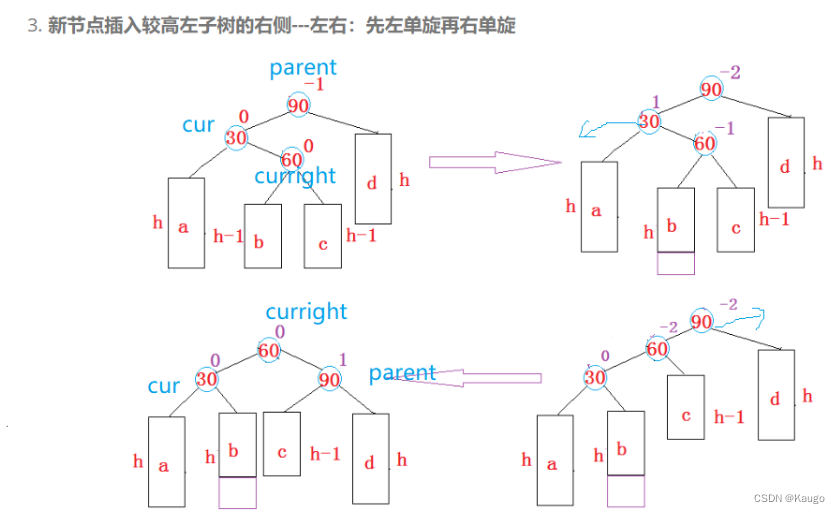
4.先左单旋再右单旋(RotateLR)
以cur为旋转点进行左旋,以parent为旋转点进行右旋,之后进行平衡因子的修改
void RotateLR(Node* parent) {Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;// 旋转之前,保存curright的平衡因子,旋转完成之后,需要根据该平衡因子来调整其他节//点的平衡因子RotateL(cur);RotateR(parent);if (bf == 0) {cur->_bf = 0;parent->_bf = 0;curright->_bf = 0;}else if (bf == -1){parent->_bf = 1;cur->_bf = 0;curright->_bf = 0;}else if (bf == 1){parent->_bf = 0;cur->_bf = -1;curright->_bf = 0;}else {assert(false);}}
三、AVL树的验证
验证其为平衡树关键点:
1.每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
2.节点的平衡因子是否计算正确
int Height(Node* root) {if (root == nullptr) {return 0;}int left = Height(root->_left);int right = Height(root->_right);return left > right ? left + 1 : right + 1;}bool IsBalance() {return IsBalance(_root);}bool IsBalance(Node* root) {if (root == nullptr) {return true;}int left = Height(root->_left);int right = Height(root->_right);if (right - left != root->_bf) {//节点的平衡因子是否计算正确cout << "平衡因子异常" << root->_kv.first << "=>" << root->_bf << endl;return false;}//每个节点子树高度差的绝对值不超过1//之后在验证左右子树return abs(right-left)<2&&IsBalance(root->_left) && IsBalance(root->_right);}
相关文章:

【C++】AVL树的插入操作实现以及验证是否正确(带平衡因子)
文章目录 前言一、AVL树结点的定义二、AVL树的插入(Insert)插入完整代码:1.左单旋(RotateL)2.右单旋(RotateR)3.先右单旋再左单旋(RotateRL)1.保存的bf为02.保存的bf为13…...
【Linux-Day10-信号量,共享内存,消息队列】
信号量 信号量描述 信号量是一个特殊的变量,一般取正数值。它的值代表允许访问的资源数目,获取资源 时,需要对信号量的值进行原子减一,该操作被称为 P 操作。 当信号量值为 0 时,代表没有资源可用,P 操作…...
使用IntelliJ IDEA本地启动调试Flink流计算工程的2个异常解决
记录:471 场景:使用IntelliJ IDEA本地启动调试Flink流计算时,报错一:加载DataStream报错java.lang.ClassNotFoundException。报错二:No ExecutorFactory found to execute the application。 版本:JDK 1.…...
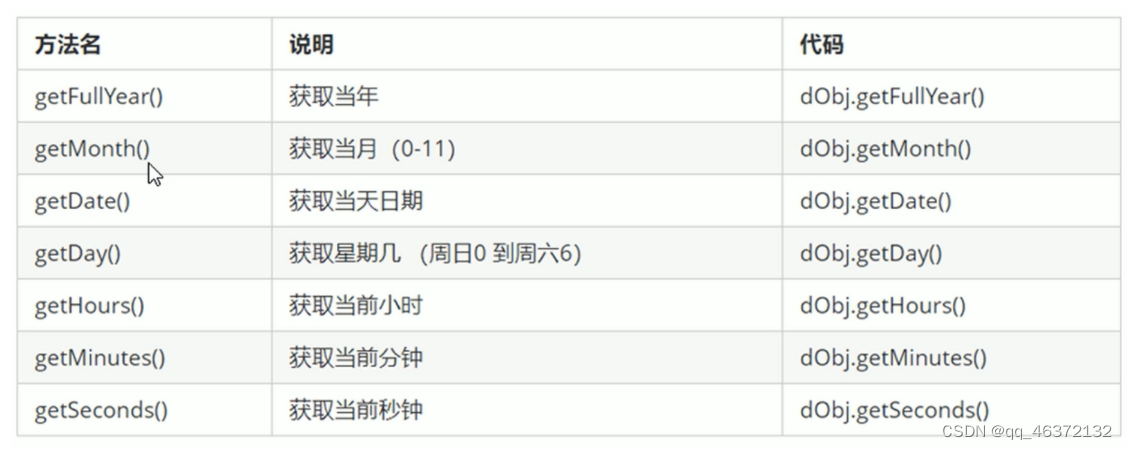
对象及日期对象
对象 1.什么是对象 类是对象的抽象,对象是类的实例 程序算法数据结构 万物皆对象,对象是一个具体的事物,看到见摸得着,对象是一组无序相关属性和方法的集合(无序,所以对象没有length属性),所有事物都是对象,列如字符串,数值,数组,函数等. 属性:事物的特征,在对象中用属性表…...

鼠标滚轮编码器解析
文章目录 前言一、鼠标滚轮编码器逻辑?二、使用步骤 1.引入库2.读入数据总结 前言 鼠标滚轮编码器为三脚接入,一个COM脚C(一般是接地),两个脉冲波形输入脚A、B,转动滚轮编码器会在两个脉冲输入脚上产生脉冲…...
【PTA】攀拓(PAT)- 程序设计(甲级)2023年春季考试
个人学习记录,代码难免不尽人意。 今天又斥资买了今年春季的真题一试,呃,感觉尽力了,89分,在当年排名23,感觉还不错,没有出现读不懂的题目和没有思路的情况,扣的11分分别是第二题两个…...

Spring Cloud Gateway 实现原理
Spring Cloud Gateway是Spring Cloud生态系统中的一个组件,用于构建基于Spring Boot的微服务架构中的网关服务。它的主要目的是提供一种灵活的方式来路由、过滤和转换HTTP请求,从而允许您构建强大、高性能的微服务应用程序。 以下是Spring Cloud Gatewa…...

嘉泰实业:真实低门槛,安全有保障
在互联网金融大行其道的当下,无论用户是多么的青睐、喜爱这种便捷的理财方式,也一定得把资金安全放在心上。要投就投那些实力背景雄厚,诚信经营的平台,可以选择投资用户基数庞大的理财老品牌,也可以选择发展势头迅猛的…...

spring boot 2.7 -> 3.0升级指南
spring boot提供一个版本迁移指南 2.7 -> 3.0...

MQTT 连接优化指南
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

算法和数据结构学习中的一些小的工具函数
算法和数据结构学习中的一些小的工具函数 作者:Grey 原文地址: 博客园:算法和数据结构学习中的一些小的工具函数 CSDN:算法和数据结构学习中的一些小的工具函数 提取一个数二进制最右侧的 1 比如二进制为:0100 0…...

解决2K/4K高分屏下Vmware等虚拟机下Kail Linux界面显示问题
问题现象 在我们日常使用VirtualBox、Vmware workstation、Hyper-V等虚拟机安装使用Kali系统,在2K/4K高分辨率电脑下Kali系统界面显示太小,包括各种软件及命令终端字体均无法很直观的看出,影响我们的正常测试及使用。 常规处理思路 很多人…...

【校招VIP】java语言考点之双亲委派模型
考点介绍: 双亲委派是校招面试中的高频考点之一。双亲委派机制定义: 当一个类加载器收到了类加载的请求的时候,他不会直接去加载指定的类,而是把这个请求委托给自己的父加载器去加载,只有父加载器无法加载这个类的时候࿰…...

2023年阿里云新用户云服务器价格表
阿里云,作为国内领先的云计算服务提供商,一直致力于为全球用户提供安全、稳定、高效的云计算服务。对于新用户来说,阿里云服务器是一个非常不错的选择。那么,阿里云新用户云服务器的价格是怎样的呢?本文将为大家详细介…...

信号相关名词概念汇总-采样周期、泄露、窗函数等
信号相关名词概念汇总-采样周期、泄露、窗函数等 以下为信号相关名词概念的汇总 1 名词解释 采样周期/间隔:采样频率的倒数,两次相邻采样之间的时间间隔采样时间:采样的总时长,即采样点数N和采样周期的乘积采样频率: …...
数字化新零售营销模式如何落地?数字化新零售营销功能推荐
通过科技手段,针对对线下零售店面的客户进行消费行为、频次等的分析,并进一步整合线上线下资源,实现实体零售的效率充分化,便是目前很火的新零售营销模式,能够将实体门店与数字化技术进行有机结合,通过为…...

712. 两个字符串的最小ASCII删除和 -- 动规
712. 两个字符串的最小ASCII删除和 class MinimumDeleteSum:"""712. 两个字符串的最小ASCII删除和https://leetcode.cn/problems/minimum-ascii-delete-sum-for-two-strings/"""def solution(self, s1: str, s2: str) -> int:""&qu…...

python中的小tips
1、注释 1、注释快捷键: Ctrl/ 可以注释掉光标所在的这一行,或者是选中的区域。 对于注释掉的这一行或者这一区域,按下ctrl/则会去掉注释。 2、多行注释 在写多行注释时,英文状态下写三个",会自动变成六个"&…...

高精度(加减乘除)
高精度算法出现的原因 当参与运算的数的范围大大的超出了标准数据类型,如int(-2147483648 ~ 2147483647)或者long long的范围,就需要使用高精度算法来进行数的运算。高精度运算的特点是代码长度比较长,本质是对数学运算…...
java企业数据管理系统
项目介绍 此项目为企业数据管理系统的后端部分,前端部分请参考vue-admin,项目实现了菜单管理、用户管理、角色管理和权限管理四个基础模块,前端菜单管理结合动态路由可自由添加菜单。结合Shiro权限管理实现了菜单和按钮的权限控制。 ❝ 前端…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

高保真组件库:开关
一:制作关状态 拖入一个矩形作为关闭的底色:44 x 22,填充灰色CCCCCC,圆角23,边框宽度0,文本为”关“,右对齐,边距2,2,6,2,文本颜色白色FFFFFF。 拖拽一个椭圆,尺寸18 x 18,边框为0。3. 全选转为动态面板状态1命名为”关“。 二:制作开状态 复制关状态并命名为”开…...

VASP软件在第一性原理计算中的应用-测试GO
VASP软件在第一性原理计算中的应用 VASP是由维也纳大学Hafner小组开发的一款功能强大的第一性原理计算软件,广泛应用于材料科学、凝聚态物理、化学和纳米技术等领域。 VASP的核心功能与应用 1. 电子结构计算 VASP最突出的功能是进行高精度的电子结构计算ÿ…...

安宝特案例丨寻医不再长途跋涉?Vuzix再次以AR技术智能驱动远程医疗
加拿大领先科技公司TeleVU基于Vuzix智能眼镜打造远程医疗生态系统,彻底革新患者护理模式。 安宝特合作伙伴TeleVU成立30余年,沉淀医疗技术、计算机科学与人工智能经验,聚焦医疗保健领域,提供AR、AI、IoT解决方案。 该方案使医疗…...
