线性代数的本质(四)
文章目录
- 行列式
- 二阶行列式
- n n n 阶行列式
- 行列式的性质
- 克拉默法则
- 行列式的几何理解
行列式
二阶行列式
行列式引自对线性方程组的求解。考虑两个方程的二元线性方程组
{ a 11 x 1 + a 12 x 2 = b 1 a 21 x 1 + a 22 x 2 = b 2 \begin{cases} a_{11}x_1+a_{12}x_2=b_1 \\ a_{21}x_1+a_{22}x_2=b_2 \end{cases} {a11x1+a12x2=b1a21x1+a22x2=b2
可使用消元法,得
( a 11 a 22 − a 12 a 21 ) x 1 = b 1 a 22 − a 12 b 2 ( a 11 a 22 − a 12 a 21 ) x 2 = a 11 b 2 − b 1 a 21 (a_{11}a_{22}-a_{12}a_{21})x_1=b_1a_{22}-a_{12}b_2 \\ (a_{11}a_{22}-a_{12}a_{21})x_2=a_{11}b_2-b_1a_{21} (a11a22−a12a21)x1=b1a22−a12b2(a11a22−a12a21)x2=a11b2−b1a21
当 a 11 a 22 − a 12 a 21 ≠ 0 a_{11}a_{22}-a_{12}a_{21}\neq 0 a11a22−a12a21=0 时,得
x 1 = b 1 a 22 − a 12 b 2 a 11 a 22 − a 12 a 21 , x 2 = a 11 b 2 − b 1 a 21 a 11 a 22 − a 12 a 21 x_1=\frac{b_1a_{22}-a_{12}b_2}{a_{11}a_{22}-a_{12}a_{21}},\quad x_2=\frac{a_{11}b_2-b_1a_{21}}{a_{11}a_{22}-a_{12}a_{21}} x1=a11a22−a12a21b1a22−a12b2,x2=a11a22−a12a21a11b2−b1a21
从方程组解来看,分母 a 11 a 22 − a 12 a 21 a_{11}a_{22}-a_{12}a_{21} a11a22−a12a21 是系数矩阵 A = [ a 11 a 12 a 21 a 22 ] A=\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\end{bmatrix} A=[a11a21a12a22] 的元素计算得到,称这个值为矩阵 A A A 的二阶行列式(determinant),记为 det A \det A detA 或 ∣ A ∣ |A| ∣A∣ ,或记为数表形式
∣ a 11 a 12 a 21 a 22 ∣ = a 11 a 22 − a 12 a 21 \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}=a_{11}a_{22}-a_{12}a_{21} a11a21a12a22 =a11a22−a12a21
利用二阶行列式的概念,分子也可写为二阶行列式
det A 1 = ∣ b 1 a 12 b 2 a 22 ∣ = b 1 a 22 − a 12 b 2 det A 2 = ∣ a 11 b 1 a 21 b 2 ∣ = a 11 b 2 − b 1 a 21 \det A_1=\begin{vmatrix} b_1 & a_{12} \\ b_2 & a_{22}\end{vmatrix}=b_1a_{22}-a_{12}b_2 \\ \det A_2=\begin{vmatrix} a_{11} & b_1 \\ a_{21} & b_2\end{vmatrix}=a_{11}b_2-b_1a_{21} detA1= b1b2a12a22 =b1a22−a12b2detA2= a11a21b1b2 =a11b2−b1a21
从上面对比可以看出, x j x_j xj 的矩阵 A j A_j Aj 是系数矩阵 A A A的第 j j j 列用常数项代替后的矩阵。这样,方程组的解可表示为
x 1 = det A 1 det A , x 2 = det A 2 det A x_1=\frac{\det A_1}{\det A},\quad x_2=\frac{\det A_2}{\det A} x1=detAdetA1,x2=detAdetA2
n n n 阶行列式
考虑三个方程的三元线性方程组,系数矩阵为
A = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{bmatrix} A= a11a21a31a12a22a32a13a23a33
用消元法可知未知数的分母同样是系数矩阵 A A A 的元素运算得到,于是定义三阶行列式为
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 11 a 23 a 32 − a 12 a 21 a 33 − a 13 a 22 a 31 \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{vmatrix} =a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32} -a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31} a11a21a31a12a22a32a13a23a33 =a11a22a33+a12a23a31+a13a21a32−a11a23a32−a12a21a33−a13a22a31
由二阶行列式的定义,上式可变为
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 ∣ a 22 a 23 a 32 a 33 ∣ − a 12 ∣ a 21 a 23 a 31 a 33 ∣ + a 13 ∣ a 11 a 12 a 21 a 22 ∣ \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{vmatrix}= a_{11}\begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33}\end{vmatrix}- a_{12}\begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33}\end{vmatrix}+ a_{13}\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\end{vmatrix} a11a21a31a12a22a32a13a23a33 =a11 a22a32a23a33 −a12 a21a31a23a33 +a13 a11a21a12a22
进一步探索 n n n 元线性方程组,可知高阶行列式定义。为书写方便,把元素 a i j a_{ij} aij 所在的行和列划掉后,剩下的元素组成的行列式称为 a i j a_{ij} aij 的余子式(cofactor),记作 M i j M_{ij} Mij ,并称
A i j = ( − 1 ) i + j M i j A_{ij}=(-1)^{i+j}M_{ij} Aij=(−1)i+jMij
为 a i j a_{ij} aij 的代数余子式(algebraic cofactor)。
定义:方阵 A A A 的行列式用第一行元素的代数余子式定义为
det A = ∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ∣ = ∑ j = 1 n a 1 j A 1 j \det A=\begin{vmatrix} a_{11}&a_{12}&\cdots&a_{1n} \\ a_{21}&a_{22}&\cdots&a_{2n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{n1}&a_{n2}&\cdots&a_{nn} \\ \end{vmatrix}=\sum_{j=1}^na_{1j}A_{1j} detA= a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann =j=1∑na1jA1j
由定义易知,行列式可以按任意行(列)展开。
det A = ∑ j = 1 n a i j A i j , by row i det A = ∑ i = 1 n a i j A i j , by col j \det A=\sum_{j=1}^na_{ij}A_{ij}, \quad \text{by row }i \\ \det A=\sum_{i=1}^na_{ij}A_{ij}, \quad \text{by col }j detA=j=1∑naijAij,by row idetA=i=1∑naijAij,by col j
行列式的性质
性质:使用数学归纳法可知
- 行列式与其转置行列式相等: det A T = det A \det A^T=\det A detAT=detA
- 互换行列式两行(列),行列式改变符号。
∣ a b c d ∣ = − ∣ c d a b ∣ \begin{vmatrix}a&b\\c&d\end{vmatrix}=-\begin{vmatrix}c&d\\a&b\end{vmatrix} acbd =− cadb - 行列式的某一行(列)所有元素同乘以数 k k k,等于数 k k k乘以该行列式。
∣ k a b k c d ∣ = k ∣ a b c d ∣ \begin{vmatrix}ka&b\\kc&d\end{vmatrix}=k\begin{vmatrix}a&b\\c&d\end{vmatrix} kakcbd =k acbd - 若行列式的某一行(列)的为两组数之和,则可表示为两行列式之和。
∣ a 1 + a 2 b c 1 + c 2 d ∣ = ∣ a 1 b c 1 d ∣ + ∣ a 2 b c 2 d ∣ \begin{vmatrix}a_1+a_2&b\\c_1+c_2&d\end{vmatrix}=\begin{vmatrix}a_1&b\\c_1&d\end{vmatrix}+\begin{vmatrix}a_2&b\\c_2&d\end{vmatrix} a1+a2c1+c2bd = a1c1bd + a2c2bd - 把行列式的某一行(列)所有元素同乘以数 k k k 都加到另一行(列)对应的元素上去,行列式的值不变。
∣ a b c d ∣ = ∣ a + k b b c + k d d ∣ \begin{vmatrix}a&b\\c&d\end{vmatrix}=\begin{vmatrix}a+kb&b\\c+kd&d\end{vmatrix} acbd = a+kbc+kdbd - 矩阵乘积的行列式等于行列式的乘积: det ( A B ) = ( det A ) ( det B ) = det ( B A ) \det(AB)=(\det A)(\det B)=\det(BA) det(AB)=(detA)(detB)=det(BA)
推论:
- 行列式中若有两行(列)元素相同,该行列式的值为零。
- 行列式中某一行(列)的公因子可以提取到行列式符号外面。
- 行列式中若有两行(列)元素成比例,则此行列式等于零。
- det ( k A ) = k n det A \det(kA)=k^n\det A det(kA)=kndetA
由上面的性质,我们很容易得到:
- 出现零行和零列的行列式为零。
- 对角阵 A = diag ( λ 1 , λ 2 , ⋯ , λ n ) A=\text{diag}(\lambda_1,\lambda_2,\cdots,\lambda_n) A=diag(λ1,λ2,⋯,λn) 的行列式 det A = λ 1 λ 2 ⋯ λ n \det A=\lambda_1\lambda_2\cdots\lambda_n detA=λ1λ2⋯λn 。
- 如果 A A A 是三角阵,行列式为主对角线元素的乘积。
对于高阶行列式,一般利用行列式的性质,初等变换化为三角行列式求解。
示例:可用数学归纳法证明范德蒙行列式(Vandermonde determinant):
∣ 1 1 ⋯ 1 a 1 a 2 ⋯ a n a 1 2 a 2 2 ⋯ a n 2 ⋮ ⋮ ⋮ ⋮ a 1 n − 1 a 2 n − 1 ⋯ a n n − 1 ∣ = ∏ 1 ⩽ i < j ⩽ n ( a j − a i ) \begin{vmatrix} 1 & 1& \cdots &1 \\ a_1 &a_2&\cdots &a_n \\ a_1^2 &a_2^2&\cdots &a_n^2 \\ \vdots &\vdots&\vdots &\vdots \\ a_1^{n-1} &a_2^{n-1}&\cdots &a_n^{n-1} \end{vmatrix}=\prod_{1⩽ i<j⩽n}(a_j-a_i) 1a1a12⋮a1n−11a2a22⋮a2n−1⋯⋯⋯⋮⋯1anan2⋮ann−1 =1⩽i<j⩽n∏(aj−ai)
行列式函数:若 A A A 为 n n n阶矩 阵,可以将 det A \det A detA 看作 A A A 中 n n n 个列向量的函数。若 A A A 中除了一列之外都是固定的向量,则 det A \det A detA 是线性函数。
假设第 j j j 列是变量,定义映射 x ↦ T ( x ) \mathbf x\mapsto T(\mathbf x) x↦T(x) 为
T ( x ) = det A = det [ a 1 ⋯ x ⋯ a n ] T(\mathbf x)=\det A=\det\begin{bmatrix}\mathbf a_1\cdots\mathbf x\cdots\mathbf a_n\end{bmatrix} T(x)=detA=det[a1⋯x⋯an]
则有
T ( c x ) = c T ( x ) T ( u + v ) = T ( u ) + T ( v ) T(c\mathbf x)=cT(\mathbf x) \\ T(\mathbf u+\mathbf v)=T(\mathbf u)+T(\mathbf v) T(cx)=cT(x)T(u+v)=T(u)+T(v)
克拉默法则
这里只讨论方程个数和未知数相等的 n n n元线性方程组
A x = b A\mathbf x=\mathbf b Ax=b
若 det A ≠ 0 \det A\neq0 detA=0,那么它有唯一解
x j = det A j ( b ) det A , ( j = 1 , 2 , ⋯ , n ) x_j=\frac{\det A_j(\mathbf b)}{\det A},\quad(j=1,2,\cdots,n) xj=detAdetAj(b),(j=1,2,⋯,n)
约定 A j ( b ) A_j(\mathbf b) Aj(b) 表示用向量 b \mathbf b b 替换矩阵 A A A的第 j j j列。
证:用 a 1 , a 2 , ⋯ , a n \mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n a1,a2,⋯,an 表示矩阵 A A A 的各列, e 1 , e 2 , ⋯ , e n \mathbf e_1,\mathbf e_2,\cdots,\mathbf e_n e1,e2,⋯,en 表示单位阵 I n I_n In 的各列。由分块矩阵乘法
A I j ( x ) = A [ e 1 ⋯ x ⋯ e n ] = [ A e 1 ⋯ A x ⋯ A e n ] = [ a 1 ⋯ b ⋯ a n ] = A j ( b ) \begin{aligned} AI_j(\mathbf x)&=A\begin{bmatrix}\mathbf e_1&\cdots&\mathbf x&\cdots&\mathbf e_n\end{bmatrix} \\ &=\begin{bmatrix}A\mathbf e_1&\cdots& A\mathbf x&\cdots& A\mathbf e_n\end{bmatrix} \\ &=\begin{bmatrix}\mathbf a_1&\cdots&\mathbf b&\cdots&\mathbf a_n\end{bmatrix} \\ &=A_j(\mathbf b) \end{aligned} AIj(x)=A[e1⋯x⋯en]=[Ae1⋯Ax⋯Aen]=[a1⋯b⋯an]=Aj(b)
由行列式的乘法性质
det A det I j ( x ) = det A j ( b ) \det A\det I_j(\mathbf x)=\det A_j(\mathbf b) detAdetIj(x)=detAj(b)
左边第二个行列式可沿第 j j j 列余子式展开求得 det I j ( x ) = x j \det I_j(\mathbf x)=x_j detIj(x)=xj。从而
x j det A = det A j ( b ) x_j\det A=\det A_j(\mathbf b) xjdetA=detAj(b)
若 det A ≠ 0 \det A\neq0 detA=0,则上式得证。
行列式的几何理解
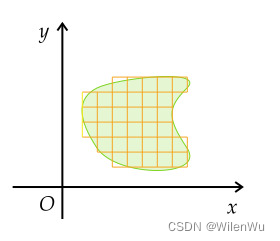
Grant:行列式告诉你一个线性变换对区域的缩放比例。
我们已经知道,线性变换保持网格线平行且等距。为了方便,我们只考虑在平面直角坐标系内,单位基向量 i , j \mathbf i,\mathbf j i,j 所围成的单位正方形区域的线性变换。
根据向量加法的平行四边形法则和线性变换基本性质知,变换后的区域为矩阵 A = [ a b c d ] A=\begin{bmatrix}a & b\\c & d\end{bmatrix} A=[acbd] 的列向量 [ a c ] \begin{bmatrix}a\\c\end{bmatrix} [ac] 和 [ b d ] \begin{bmatrix}b\\d\end{bmatrix} [bd] 为邻边的平行四边形区域。
结论:二阶行列式的值表示由 A A A 的列确定的有向平行四边形的面积。
(1) 若 A A A 为对角阵,显然行列式 det [ a b 0 d ] \det\begin{bmatrix}a & b\\0 & d\end{bmatrix} det[a0bd] 表示底为 a a a,高为 d d d 的平行四边形面积

(2) 更一般的情况 A = [ a b c d ] A=\begin{bmatrix}a & b\\c & d\end{bmatrix} A=[acbd] ,可以看出,行列式的值与面积有着紧密的联系。

(3) 矩阵 [ a 2 a a 1 ] \begin{bmatrix}a^2 & a\\a & 1\end{bmatrix} [a2aa1] 表示将单位正方形压缩成线段,面积自然为0,行列式的值为0

单位正方形区域缩放的比例,其实可以代表任意给定区域缩放的比例。这是因为,线性变换保持网格线平行且等距。对于空间中任意区域的面积,借助微积分的思想,我们可以采用足够的小方格来逼近区域的面积,对所有小方格等比例缩放,则整个区域也以同样的比例缩放。
volume T ( Ω ) = ( det T ) ( volume Ω ) \text{volume }T(\Omega) = (\det T)(\text{volume }\Omega) volume T(Ω)=(detT)(volume Ω)
通过行列式的几何意义,我们就建立了线性变换、矩阵、行列式之间的关系。不难得出
- 复合线性变换缩放的比例相当于每次变换缩放比例的乘积,即
det A B = det A det B \det AB=\det A\det B detAB=detAdetB - 行列式的值为零,表示将空间压缩到更低的维度,矩阵的列向量线性相关
相关文章:

线性代数的本质(四)
文章目录 行列式二阶行列式 n n n 阶行列式行列式的性质克拉默法则行列式的几何理解 行列式 二阶行列式 行列式引自对线性方程组的求解。考虑两个方程的二元线性方程组 { a 11 x 1 a 12 x 2 b 1 a 21 x 1 a 22 x 2 b 2 \begin{cases} a_{11}x_1a_{12}x_2b_1 \\ a_{21}x_…...
FreeMarker详细介绍
FreeMarker详细介绍 FreeMarker FreeMarker概述 FreeMarker概念 FreeMarker 是一款 模板引擎: 即一种基于模板和要改变的数据, 并用来生成输出文本(HTML网页,电子邮件,配置文件,源代码等)的通用工具。 是一个Java类库…...
房地产小程序 | 小程序赋能,房地产业务数字化升级
随着科技的不断发展,房地产行业正逐渐向数字化转型。在这个过程中,房地产小程序成为了一种重要的工具,可以帮助房地产企业提供更好的购房体验、增加销售额,并实现管理的便捷化。 优点 便捷购房体验:房地产小程序为用户…...

Databend 开源周报第 110 期
Databend 是一款现代云数仓。专为弹性和高效设计,为您的大规模分析需求保驾护航。自由且开源。即刻体验云服务:https://app.databend.cn 。 Whats On In Databend 探索 Databend 本周新进展,遇到更贴近你心意的 Databend 。 使用 BendSQL 管…...
开源大模型ChatGLM2-6B 1. 租一台GPU服务器测试下
0. 环境 租用了1台GPU服务器,系统 ubuntu20,GeForce RTX 3090 24G。过程略。本人测试了ai-galaxy的,今天发现网友也有推荐autodl的。 (GPU服务器已经关闭,因此这些信息已经失效) SSH地址:* 端…...

SQL10 用where过滤空值练习
描述 题目:现在运营想要对用户的年龄分布开展分析,在分析时想要剔除没有获取到年龄的用户,请你取出所有年龄值不为空的用户的设备ID,性别,年龄,学校的信息。 示例:user_profile iddevice_idge…...

JVM--Hotspot Architecture 详解
一、Java Virtual Machine (JVM)概述 Java Virtual Machine 虚拟机 (JVM) 是一种抽象的计算机。JVM本身也是一个程序,但是对于编写在其中执行的程序来说,它看起来像一台机器。对于特定的操作系统ÿ…...

ThreadLocal功能实现
模拟ThreadLocal功能实现 当前线程任意方法内操作连接对象 一个栈对应一个线程 , 一个方法调用另一个方法都是在一个线程内 , 只有执行了线程的start方法才会创建一个线程 定义一个Map集合 , key是当前线程(Thread.currentThread) , value是要绑定的数据(Connection对象) 以…...
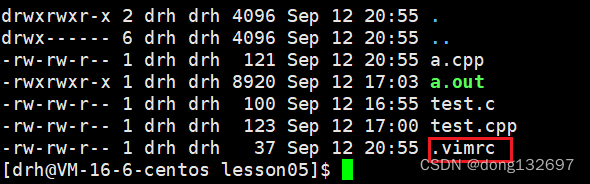
Linux编辑器-vim使用
文章目录 前言一、vim编辑器1、vim的基本概念2、vim的基本操作2.1 命令模式切换至插入模式2.2 插入模式切换至命令模式2.3 命令模式切换至底行模式 3、vim命令模式命令集3.1 移动光标3.2 删除文字3.3 复制与粘贴3.4 替换3.5 撤销上一次操作3.6 更改3.7 跳至指定的行 4、vim末行…...
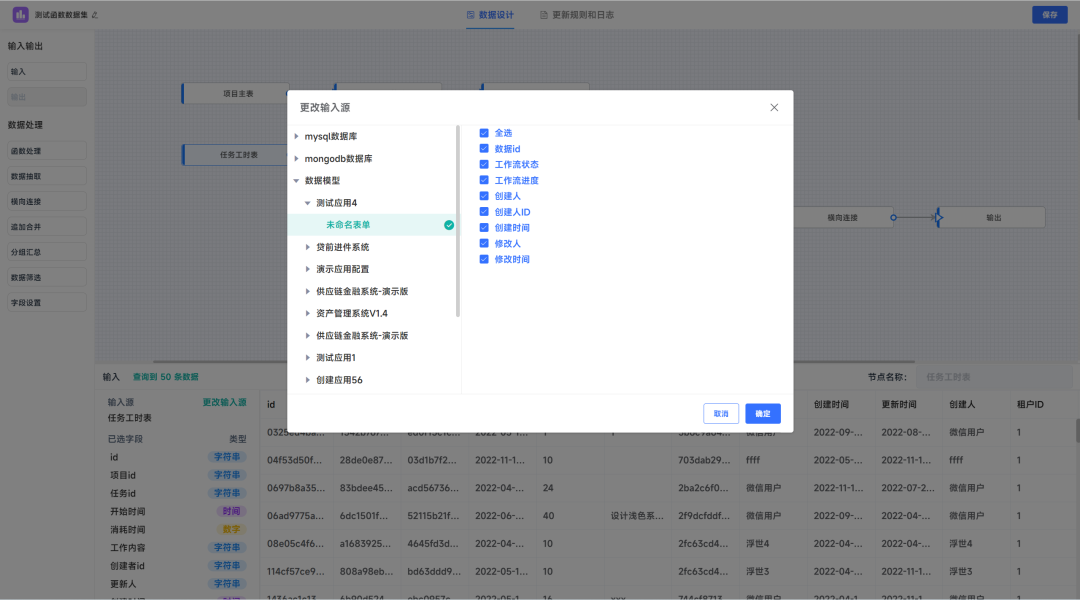
自助式数据分析平台:JVS智能BI功能介绍(二)数据集管理
数据集是JVS-智能BI中承载数据、使用数据、管理数据的基础,同样也是构建数据分析的基础。可以通俗地将其理解为数据库中的普通的表,他来源于智能的ETL数据加工工具,可以将数据集进行分析图表、统计报表、数字大屏、数据服务等制作。 在整体的…...

《5G技术引领教育信息化新革命》
5G技术引领教育信息化新革命 随着5G技术的快速发展,教育领域也迎来了全新的信息化时代。5G技术为教育行业提供了更高速、更稳定、更智能的网络连接,使得教育信息化不再局限于传统的课堂教学,而是延伸到了线上、线下的全时空教育。本文将详细介…...

cmake学习过程记录
目录 基础命令学习配置opencvcmake (Windows版本) 基础命令学习 //设置最低版本号 cmake_minimum_required(VERSION 3.5)//设置项目名称 project (hello_headers)//递归遍历文件夹src中的cpp文件放到变量SOURCES中 file(GLOB_RECURSE SOURCES src/*.cpp)//设置目标exe名称…...
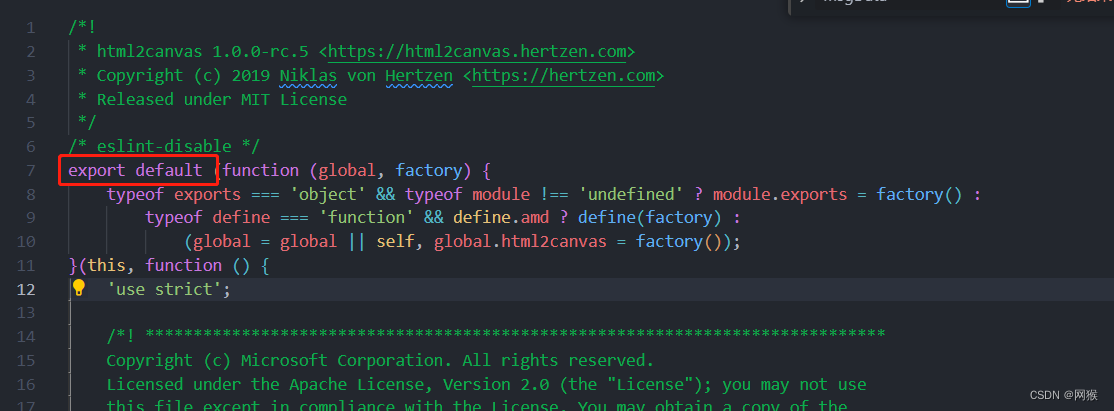
Vue3、Vite使用 html2canvas 把Html生成canvas转成图片并保存,以及填坑记录
这两天接到新需求就是生成海报分享,生成的格式虽然是一样的但是自己一点点画显然是不符合我摸鱼人的性格,就找到了html2canvas插件,开始动工。 安装 npm install html2canvas --save文档 options 的参数都在里面按照自己需求使用 https://a…...
)
centos yum源配置(CentOS7 原生 yum 源修改为阿里 yum 源)
文章目录 centos yum源配置centos搭建内网yum源内网centos的yum软件源配置CentOS7 原生 yum 源修改为阿里 yum 源 centos yum源配置 centos搭建内网yum源 您好,在CentOS系统上搭建本地内网YUM仓库的方法如下: 安装httpd和createrepo工具 yum install httpd createrepo -y创…...
linux————ansible
一、认识自动化运维 自动化运维: 将日常IT运维中大量的重复性工作,小到简单的日常检查、配置变更和软件安装,大到整个变更流程的组织调度,由过去的手工执行转为自动化操作,从而减少乃至消除运维中的延迟,实现“零延时”…...

初识Java 8-1 接口和抽象类
目录 抽象类和抽象方法 接口定义 默认方法 多重继承 接口中的静态方法 作为接口的Instrument 本笔记参考自: 《On Java 中文版》 接口和抽象类提供了一种更加结构化的方式分离接口和实现。 抽象类和抽象方法 抽象类,其介于普通类和接口之间。在构…...

微信小程序音频后台播放功能
微信小程序在手机息屏后依旧能播放音频,需要使用 wx.getBackgroundAudioManager() 方法创建后台音乐播放器,并将音乐播放任务交给这个后台播放器。 具体实现步骤如下: 小程序页面中,使用 wx.getBackgroundAudioManager() 方法创…...
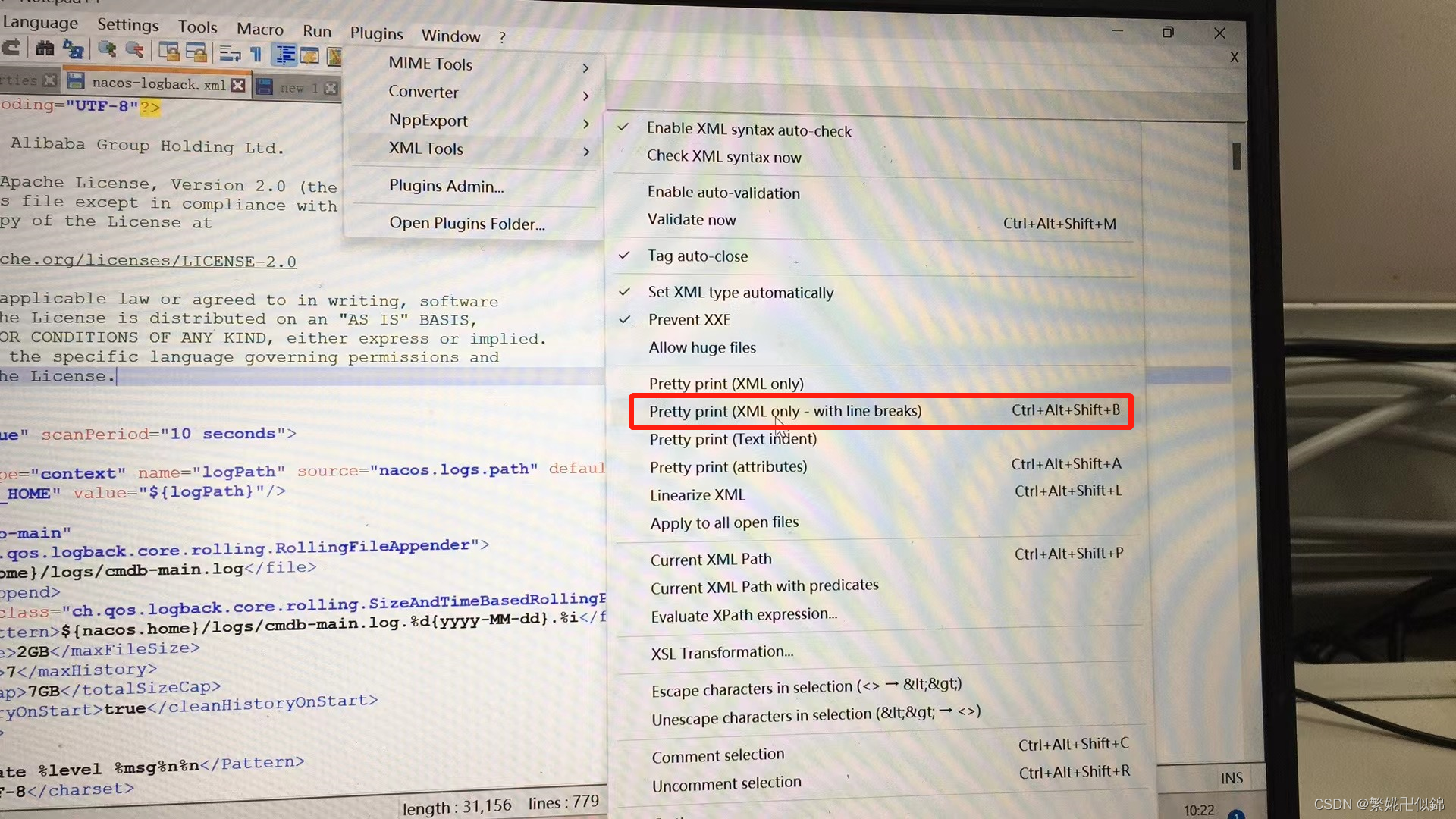
NotePad——xml格式化插件xml tools在线安装+离线安装
在使用NotePad时,在某些情形下,需要格式化Xml格式内容,可以使用Xml Tools插件。 一、在线安装 1. 打开Notepad 软件 2. 选择插件,选择“插件管理” 3. 搜索 XML Tools,找到该插件后,勾选该文件ÿ…...

图书管理系统 数据结构先导课暨C语言大作业复习 | JorbanS
问题描述 读取给定的图书文件book.txt中的信息(book.txt中部分图书信息如下图所示),完成一个图书信息管理系统,该系统的各个功能模块要求利用菜单选项进行选择。 系统功能要求 图书浏览 读取book.txt中的文件信息并依次输出所…...
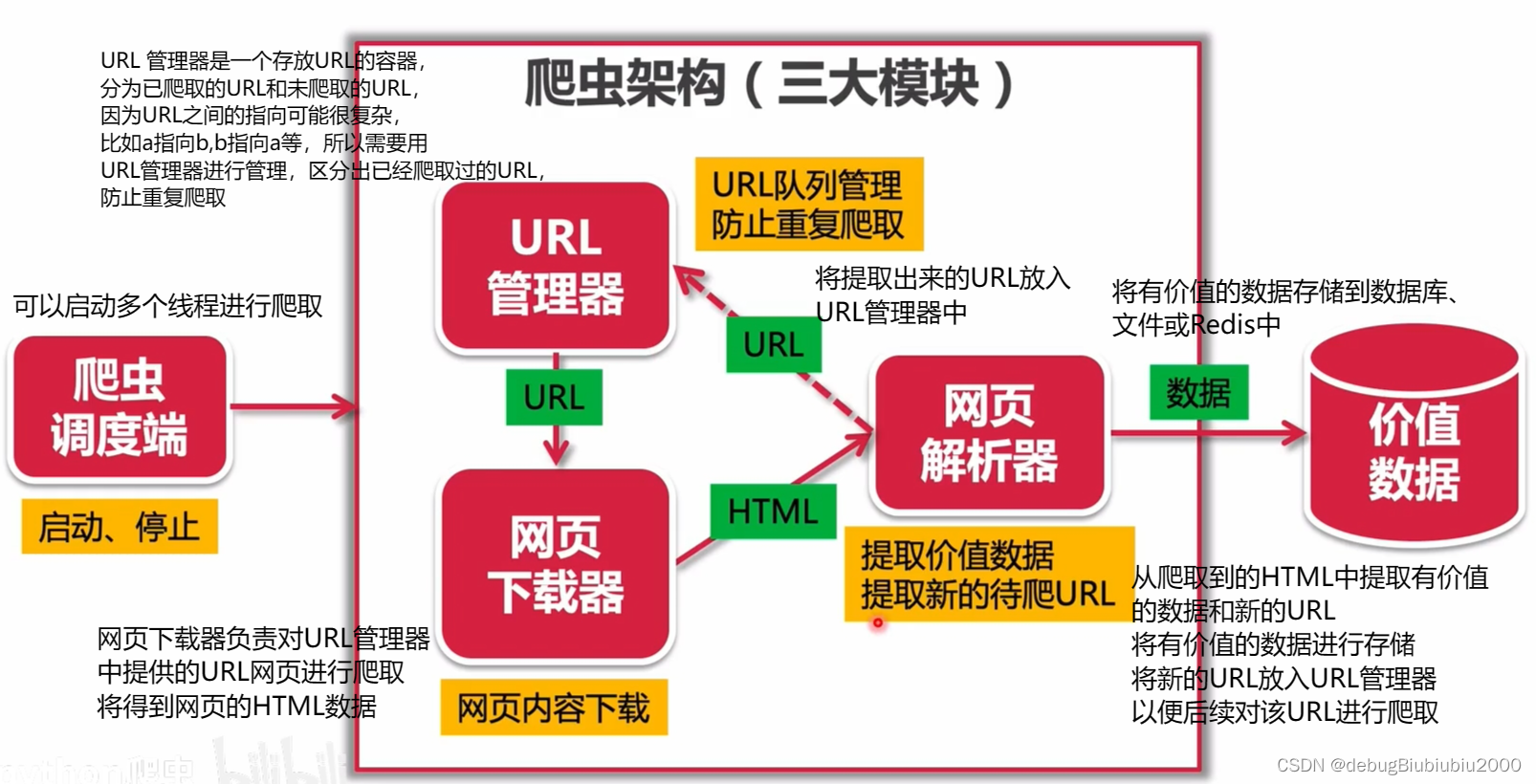
python 爬虫的开发环境配置
1、新建一个python项目 2、在控制台中分别安装下面三个包 pip install requests pip install beautifulsoup4 pip install selenium/ 如果安装时报以下错误: raise ReadTimeoutError(self._pool, None, "Read timed out.") pip._vendor.urllib3.exceptio…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
