《DATASET DISTILLATION》
这篇文章提出了数据浓缩的办法,在前面已有的知识浓缩(压缩模型)的经验上,提出了不压缩模型,转而压缩数据集的办法,在压缩数据集上训练模型得到的效果尽可能地接近原始数据集的效果。
摘要
模型蒸馏的目的是将复杂模型的知识提炼为简单模型的知识。在本文中考虑了一个替代的公式,称为数据集蒸馏:我们保持模型固定,而不是尝试从一个大的训练数据集提取知识到一个小的。其思想是合成少量的数据点,这些数据点不需要来自于正确的数据分布,但当给学习算法作为训练数据时,会近似于在原始数据上训练的模型。例如,文章展示了可以将6万幅MNIST训练图像压缩成10幅合成蒸馏图像(每类一张),在给定一个固定的网络初始化条件下,只需几个梯度下降步骤,就可以达到接近原始性能的效果。
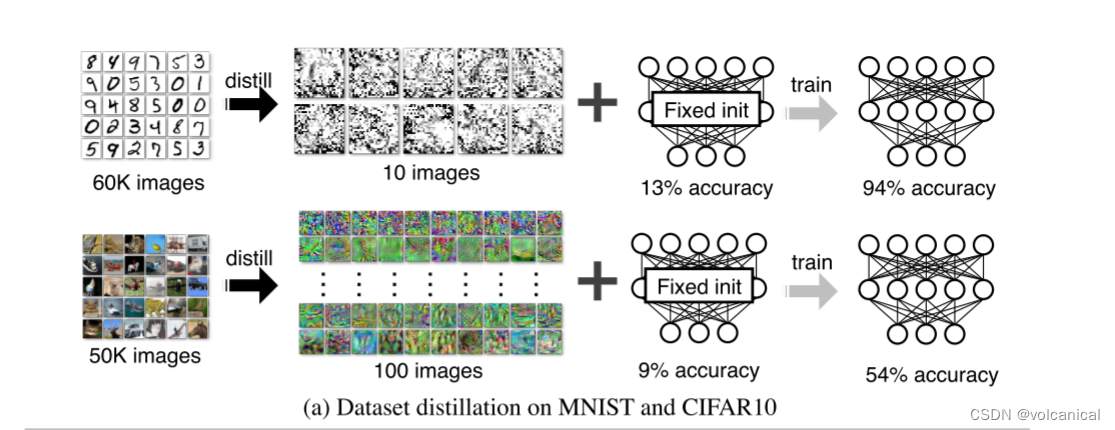
效果1:使用压缩后的图片进行训练,10张MNIST或者100张CIFAR10,就可以达到94%的准确率和54%的准确率。
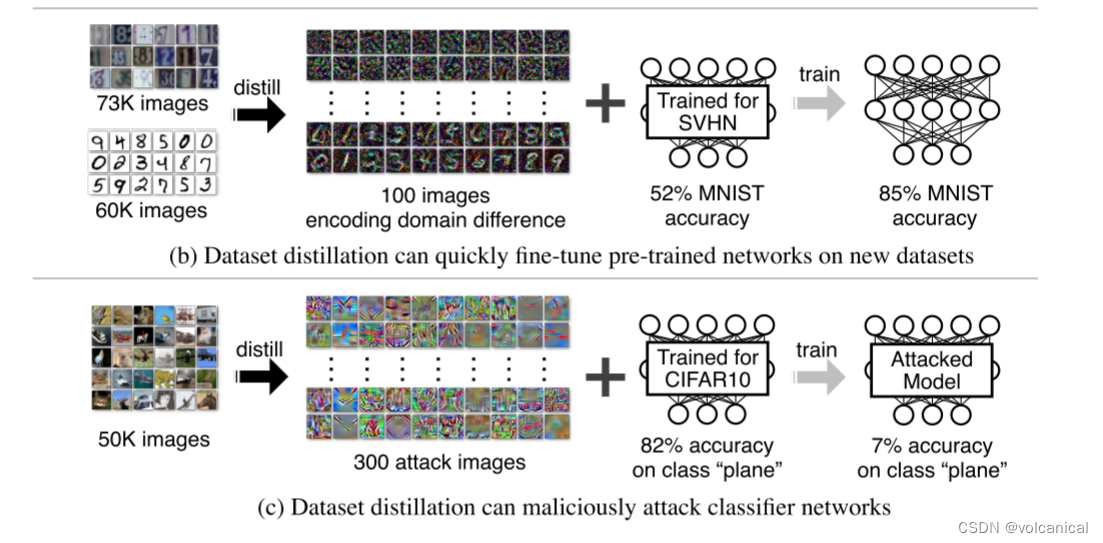
效果2:使用压缩数据进行fine-tune,可以很好地微调数据集效果。
效果3:将攻击数据集浓缩,可以更好地强化攻击的效果,仅仅用300张图片就使得目标类的分类准确率降低至7%。
相关工作:
Pass
方法:
准备工作
考虑有数据集 x = { x i } i = 1 N \mathbf{x}=\left\{x_i\right\}_{i=1}^N x={xi}i=1N为原始数据集,神经网络为 θ \theta θ, ℓ ( x i , θ ) \ell\left(x_i, \theta\right) ℓ(xi,θ)是 x i x_i xi在模型 θ \theta θ上的损失。
θ ∗ = arg min θ 1 N ∑ i = 1 N ℓ ( x i , θ ) ≜ arg min θ ℓ ( x , θ ) \theta^*=\underset{\theta}{\arg \min } \frac{1}{N} \sum_{i=1}^N \ell\left(x_i, \theta\right) \triangleq \underset{\theta}{\arg \min } \ell(\mathbf{x}, \theta) θ∗=θargminN1i=1∑Nℓ(xi,θ)≜θargminℓ(x,θ)
上式就是神经网络优化的最终目标,训练获得一个 θ ∗ \theta^* θ∗使得模型在数据集上的损失最小。
这里为了方便,直接将
ℓ ( x , θ ) \ell(\mathbf{x}, \theta) ℓ(x,θ)
记为数据集上的损失平均和
优化浓缩数据
浓缩数据和浓缩学习率都是随机初始化的,通过不断地计算损失梯度下降,优化得到最终的浓缩数据集以及浓缩学习率,如何获得优化函数便是这里的重点。
x ~ = { x ~ i } i = 1 M \tilde{\mathbf{x}}=\left\{\tilde{x}_i\right\}_{i=1}^M x~={x~i}i=1M中 M ≪ N M \ll N M≪N 并且对应的学习率 η ~ \tilde{\eta} η~,对应的梯度下降为:
θ 1 = θ 0 − η ~ ∇ θ 0 ℓ ( x ~ , θ 0 ) \theta_1=\theta_0-\tilde{\eta} \nabla_{\theta_0} \ell\left(\tilde{\mathbf{x}}, \theta_0\right) θ1=θ0−η~∇θ0ℓ(x~,θ0)
使用生成的浓缩数据集 x ~ \tilde{\mathbf{x}} x~ 可以极大地增强训练的效果。给定一个初始的 θ 0 \theta_0 θ0,我们获得 x ~ \tilde{\mathbf{x}} x~ 和学习率 η ~ \tilde{\eta} η~ 通过最小化以下损失函数 L \mathcal{L} L :
x ~ ∗ , η ~ ∗ = arg min x ~ , η ~ L ( x ~ , η ~ ; θ 0 ) = arg min x ~ , η ~ ℓ ( x , θ 1 ) = arg min x ~ , η ~ ℓ ( x , θ 0 − η ~ ∇ θ 0 ℓ ( x ~ , θ 0 ) ) , \tilde{\mathbf{x}}^*, \tilde{\eta}^*=\underset{\tilde{\mathbf{x}}, \tilde{\eta}}{\arg \min } \mathcal{L}\left(\tilde{\mathbf{x}}, \tilde{\eta} ; \theta_0\right)=\underset{\tilde{\mathbf{x}}, \tilde{\eta}}{\arg \min } \ell\left(\mathbf{x}, \theta_1\right)=\underset{\tilde{\mathbf{x}}, \tilde{\eta}}{\arg \min } \ell\left(\mathbf{x}, \theta_0-\tilde{\eta} \nabla_{\theta_0} \ell\left(\tilde{\mathbf{x}}, \theta_0\right)\right), x~∗,η~∗=x~,η~argminL(x~,η~;θ0)=x~,η~argminℓ(x,θ1)=x~,η~argminℓ(x,θ0−η~∇θ0ℓ(x~,θ0)),
现在看着可能会很抽象,这里简单的讲解一下,方法就是:
- 先使用随机初始化的 x ~ \tilde{\mathbf{x}} x~和 η ~ \tilde{\eta} η~,将浓缩数据集 x ~ \tilde{\mathbf{x}} x~和浓缩学习率 η ~ \tilde{\eta} η~丢入神经网络 θ 0 \theta_0 θ0进行一轮训练。
- 使用原始数据集 检验 使用浓缩数据集 x ~ \tilde{\mathbf{x}} x~和浓缩学习率 η ~ \tilde{\eta} η~训练得到的新一轮神经网络 θ 1 \theta_1 θ1,计算原始数据集在这个模型上的损失。
- 这个损失就是我们的优化目标,我们要让这个损失最小。
模型随机初始化
上面的函数中,模型总是使用 θ 0 \theta_0 θ0进行训练获得浓缩数据集和浓缩学习率,作者担心这样获得的浓缩数据集和浓缩学习率会和 θ 0 \theta_0 θ0有较大的关系,不能很好地泛化到其他初始化,因此作者又提出使用随机的 θ 0 \theta_0 θ0来训练。
于是作者就改成,每一轮的 θ \theta θ都不同, θ 0 \theta_0 θ0是一个满足 p ( θ ) p(\theta) p(θ)的分布。
SGD下降法
每次选中一个batch,每个batch使用不同的初始化,就是把之前的GD修改为minibatch梯度下降。
具体算法如下图所示:
将原始数据集划分为 x t x_t xt的batch,每一个batch有不同的初始化 θ 0 \theta_0 θ0,每一个batch的计算方法与前面相同,最后将每个batch计算获得的 x ~ \tilde{\mathbf{x}} x~和 η ~ \tilde{\eta} η~平均。
相关文章:

《DATASET DISTILLATION》
这篇文章提出了数据浓缩的办法,在前面已有的知识浓缩(压缩模型)的经验上,提出了不压缩模型,转而压缩数据集的办法,在压缩数据集上训练模型得到的效果尽可能地接近原始数据集的效果。 摘要 模型蒸馏的目的是…...

GDPU 数据结构 天码行空1
1. 病历信息管理 实现病历查询功能。具体要求如下: 定义一个结构体描述病人病历信息(病历号,姓名,症状);完成功能如下: 输入功能:输入5个病人的信息; 查询功能:输入姓名,在5个病历中进行查找,如果找到则显示该人的信息,…...

【C++】红黑树的模拟实现
🌇个人主页:平凡的小苏 📚学习格言:命运给你一个低的起点,是想看你精彩的翻盘,而不是让你自甘堕落,脚下的路虽然难走,但我还能走,比起向阳而生,我更想尝试逆风…...
【多线程】Thread 类 详解
Thread 类 详解 一. 创建线程1. 继承 Thread 类2. 实现 Runnable 接口3. 其他变形4. 多线程的优势-增加运行速度 二. Thread 类1. 构造方法2. 常见属性3. 启动线程-start()4. 中断线程-interrupt()5. 线程等待-join()6. 线程休眠-sleep()7. 获取当前线程引用 三. 线程的状态1. …...

LINUX 网络管理
目录 一、NetworkManager的特点 二、配置网络 1、使用ip命令临时配置 1)查看网卡在网络层的配置信息 2)查看网卡在数据链路层的配置信息 3)添加或者删除临时的网卡 4)禁用和启动指定网卡 2、修改配置文件 3、nmcli命令行…...
refresh rate
1920 x 1080 显卡刷新率 60...

使用 NGINX Unit 实施应用隔离
原文作者:Artem Konev - Senior Technical Writer 原文链接:使用 NGINX Unit 实施应用隔离 转载来源:NGINX 中文官网 NGINX 唯一中文官方社区 ,尽在 nginx.org.cn NGINX Unit 特性集的最新动态之一是支持应用隔离,该特…...

2023/09/12 qtc++
实现一个图形类(Shape) ,包含受保护成员属性:周长、面积, 公共成员函数:特殊成员函数书写 定义一个圆形类(Circle) ,继承自图形类,包含私有属性:半径 公共成员函数:特殊成员函数…...
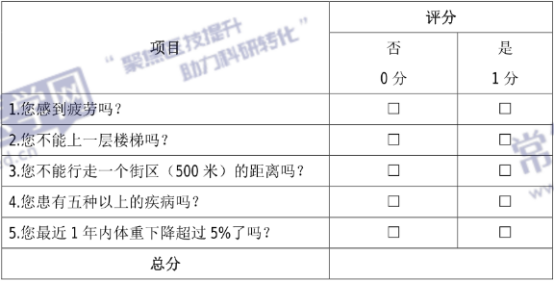
全科医学科常用评估量表汇总,建议收藏!
根据全科医学科医生的量表使用情况,笔者整理了10个常用的全科医学科量表,可在线评测直接出结果,可转发使用,可生成二维码使用,可创建项目进行数据管理,有需要的小伙伴赶紧收藏! 日常生活能力量表…...
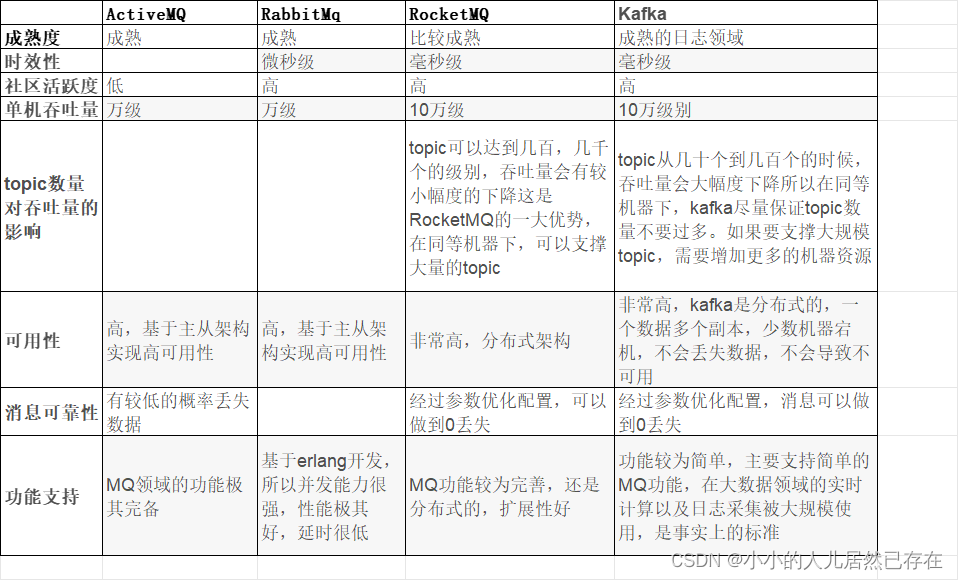
了解消息中间件的基础知识
为什么要使用消息中间件? 解耦:消息中间件可以使不同的应用程序通过解耦的方式进行通信,减少系统间的依赖关系提供异步通信:消息中间件可以实现异步消息传递,提高系统的响应性能。流量削峰:消息中间件可以…...
【linux】Linux wps字体缺失、加粗乱码解决
解决wps字体缺失问题 1、下载字体包 git clone https://github.com/iamdh4/ttf-wps-fonts.git2、创建单独放置字体的目录 mkdir /usr/share/fonts/wps-fonts3、复制字体到系统目录下 cp ttf-wps-fonts/* /usr/share/fonts/wps-fonts4、修改字体权限 chmod 644 /usr/share/f…...
 513找树左下角的值(队列))
每日两题 103二叉树的锯齿形层序遍历(数组) 513找树左下角的值(队列)
103 题目 103 给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。 示例 1: 输入:root [3,9,…...

ROS2报错:ImportError: cannot import name ‘Log‘ from ‘rosgraph_msgs.msg‘
在使用ros2的bag命令查看数据集信息时报错 Traceback (most recent call last):File "/opt/ros/noetic/bin/rosbag", line 34, in <module>import rosbagFile "/opt/ros/noetic/lib/python3/dist-packages/rosbag/__init__.py", line 33, in <mo…...

【Vue】Vue中的代码分为哪几种类型?
在 Vue 中的代码可以分为以下几种类型: 1.模板代码 模板代码是 Vue 中用来生成 HTML 的一种语法,可以通过 Vue 的模板语法和指令来动态渲染页面。模板代码一般写在 Vue 组件的 template 标签中。 2.JavaScript 代码 JavaScript 代码是 Vue 组件中用来…...

es6中includes用法
js中的includes用法 1.数组 includes 可以判断一个数组中是否包含某一个元素,并返回true 或者false [a,b,c].includes(a) true [a,b,c].includes(1) false includes可以包含两个参数,第二个参数表示判断的起始位置 起始位置第一个数字是0。 2.字符串 …...

QT中QRadioButton实现分组C++
通过对QRadioButton组件进行分组可解决QRadioButton组件的互斥性 实现如下。 假设已设计好UI并且有UI代码情况: 头文件引用: #include <QButtonGroup> 分组功能 ,cpp文件代码实现: Your_Project::Your_Project(QWidge…...
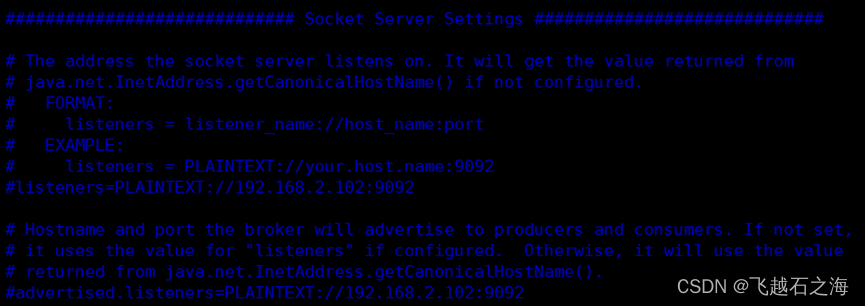
kafka实战报错解决问题
需求 在一个在线商城中,用户下单后需要进行订单的处理。为了提高订单处理的效率和可靠性,我们使用Kafka来实现订单消息的异步处理。当用户下单后,订单信息会被发送到Kafka的一个Topic中,然后订单处理系统会从该Topic中消费订单消…...
vite+react 使用 react-activation 实现缓存页面
对应的版本 "react": "^18.2.0", "react-activation": "^0.12.4", "react-dom": "^18.2.0", "react-router-dom": "^6.15.0",react-activation 这是一个npm包,在react keep alive…...

【android 蓝牙开发——蓝牙耳机】
【android 蓝牙开发——传统蓝牙】 【android 蓝牙开发——BLE(低功耗)蓝牙 2021-10-09更新】 总结一下蓝牙开发的基本使用以及蓝牙耳机的断开和链接。 所以需权限: <uses-permission android:name"android.permission.ACCESS_FIN…...
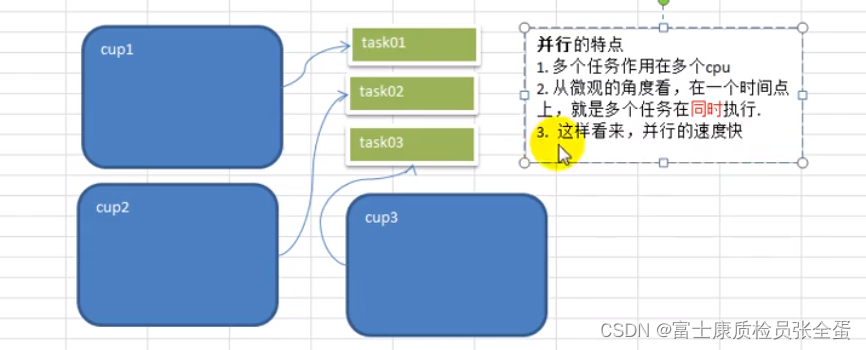
Golang goroutine 进程、线程、并发、并行
goroutine 看一个需求 需求:要求统计1-200000000000的数字中,哪些是素数? 分析思路: 1)传统的方法,就是使用一个循环,循环的判断各个数是不是素数(一个任务就分配给一个cpu去做,这样很不划算…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
