《计算机视觉中的多视图几何》笔记(1)
1 Introduction – a Tour of Multiple View Geometry
本章介绍了本书的主要思想。
1.1 Introduction – the ubiquitous projective geometry
为了了解为什么我们需要射影几何,我们从熟悉的欧几里得几何开始。 欧几里得几何在二维中认为平行线是不会相交的,解决这个问题的一种常见手段是说平行线“在无穷远”相交。 然而,这并不完全令人信服,并且与另一个格言相冲突,即无穷不存在,而只是一个方便的虚构。 我们可以通过在平行线相交的无穷远处添加这些点来增强欧几里得平面,并通过将它们称为“理想点”来解决无穷远的困难,从而解决这个问题。
通过将这些无穷远点相加,熟悉的欧几里得空间就转变为一种新型的几何对象,即射影空间。 这是一种非常有用的思维方式,因为我们熟悉欧几里得空间的属性,涉及距离、角度、点、线和入射等概念。 射影空间并没有什么非常神秘的地方——它只是欧几里得空间的延伸,其中两条线总是交汇于一点,尽管有时交汇于无穷远的点。
一个简单的2D欧式点(x, y)可以添加一个额外的坐标变为(x, y, 1),也可以表示为(kx, ky, k)。那么,我们可以观察到,虽然 (x, y, 1) 表示与坐标对 (x, y) 相同的点,但没有对应于 (x, y, 0) 的点。 如果我们尝试除以最后一个坐标,我们会得到无穷大的点 (x/0, y/0)。 这就是无穷远点的产生方式。 它们是由齐次坐标表示的点,其中最后一个坐标为零。所以,(x, y, 0)表示无穷远点。
平移和旋转被称为欧式变换,射影变换是相当于在齐次坐标下面乘了一个齐次矩阵,这是机器视觉和图形学、机器人中常见的表示方法。更通用的变换类型是线性变换,然后移动空间原点的欧几里得变换。 我们可以将其视为空间在不同方向上以不同比例移动、旋转并最终线性拉伸,由此产生的变换称为仿射变换。
1.2 Camera projections
摄像机投影的原理可以看成是从射影空间到射影平面的投影,通过一个3x4的矩阵转换一下齐次坐标就可以。
摄像机可以被视作一个点。
关于相机,如果一个相机中能够得到IAC(绝对二次曲线的图像),那么我们说相机已经标定。
1.3 Reconstruction from more than one view
考虑两幅图的重建,重构往往是会产生很多组解的。必须至少有7个不在临界位置的点,来确定重构的结果。
我们的目标是已知两幅图中的对应点,想要获取他们的相机坐标和对应的3D坐标,这种求解一定是带有不确定性的,不确定性可以用投影变换来描述,这种重建叫做投影重建。
重建的基本方法是找基础矩阵,基础矩阵意味着两个图像的对应相同的3D点。
重建的主要流程:找基础矩阵,求相机矩阵,在用三角法求对应的3D点。
1.4 Three-view geometry
对应三幅图的重建,基本原理跟两视角重建差不多,不过计算起来会更复杂。
1.5 Four view geometry and n-view reconstruction
对多视图的重建,针对不同序列有不同的重建方法,一个基本的步骤是bundle adjustment,这一步需要反复迭代式的调整。
1.6 Transfer
我们已经讨论了从一组图像进行 3D 重建。 射影几何的另一个有用的应用是传递:给定一个(或多个)图像中的点的位置,确定它在该组的所有其他图像中出现的位置。 为此,我们必须首先使用(例如)一组辅助点对应关系来建立摄像机之间的关系。
1.7 Euclidean reconstruction
欧式几何的重建,根本任务是要找绝对二次曲线所在的平面和无穷远的平面。只要找到了这两个平面,所有的欧式几何结构都将被知道。
1.8 Auto-calibration
相关文章:
)
《计算机视觉中的多视图几何》笔记(1)
1 Introduction – a Tour of Multiple View Geometry 本章介绍了本书的主要思想。 1.1 Introduction – the ubiquitous projective geometry 为了了解为什么我们需要射影几何,我们从熟悉的欧几里得几何开始。 欧几里得几何在二维中认为平行线是不会相交的&…...

YOLO目标检测——火焰检测数据集+已标注xml和txt格式标签下载分享
实际项目应用:火灾预警系统、智能监控系统、工业安全管理、森林火灾监测以及城市规划和消防设计等应用场景中具有广泛的应用潜力,可以提高火灾检测的准确性和效率,保障人员和财产的安全。数据集说明:YOLO火焰目标检测数据集&#…...

tkinter四大按钮:Button,Checkbutton, Radiobutton, Menubutton
文章目录 四大按钮Button连击MenubuttonCheckbuttonRadiobutton tkinter系列: GUI初步💎布局💎绑定变量💎绑定事件💎消息框💎文件对话框控件样式扫雷小游戏💎强行表白神器 四大按钮 tkinter中…...

Sudowrite:基于人工智能的AI写作文章生成工具
【 产品介绍】 名称 Sudowrite 成立/上线时间 2023年 具体描述 Sudowrite是一个基于GPT-3的人工智能写作工具,可以帮助你快速生成高质量的文本内容, 无论是小说、博客、营销文案还是学术论文。 Sudowrite可以根据你的输入和指…...

加密狗软件有什么作用?
加密狗软件是一种用于加密和保护计算机软件和数据的安全设备。它通常是一个硬件设备,可以通过USB接口连接到计算机上。加密狗软件的作用主要体现在以下几个方面: 软件保护:加密狗软件可以对软件进行加密和授权,防止未经授权的用户…...

嵌入式Linux驱动开发(I2C专题)(二)
I2C系统的重要结构体 参考资料: Linux驱动程序: drivers/i2c/i2c-dev.cI2CTools: https://mirrors.edge.kernel.org/pub/software/utils/i2c-tools/ 1. I2C硬件框架 2. I2C传输协议 3. Linux软件框架 4. 重要结构体 使用一句话概括I2C传输:APP通过I2…...

SMT贴片制造:发挥的作用和价值]
SMT贴片制造作为一项重要的电子制造技术,发挥着举足轻重的作用,并提供了巨大的价值。 首先,SMT贴片制造为电子产品的制造商提供了高效、准确和可靠的生产方式。相比于传统的手工焊接,SMT贴片制造具有更高的自动化和智能化程度&am…...
)
蓝桥杯官网练习题(幸运数字)
问题描述 小蓝认为如果一个数含有偶数个数位,并且前面一半的数位之和等于后面一半的数位之和,则这个数是他的幸运数字。例如 2314 是一个幸运数字, 因为它有 4 个数位, 并且 2314 。现在请你帮他计算从 1 至 100000000 之间共有多少个不同的幸运数字。 …...
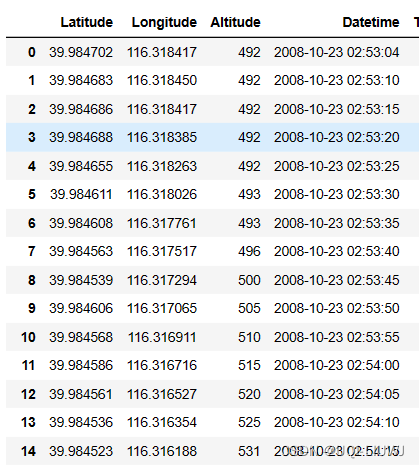
pandas笔记:显示中间的省略号
比如我们有这样一个数据(Geolife中的数据) 如何把中间的省略号完整地输出呢? pd.set_option(display.max_rows, None) data...

解决vagrant安装的centos7,在window主机重装系统过后,再次用vagrant启动centos7却无法启动
场景: vagrant安装的centos7,在window主机重装系统过后,再次用vagrant启动centos7却无法启动 检查 VirtualBox 版本:确保你安装的 VirtualBox 版本与 Vagrant 兼容。如果你更新了 VirtualBox,可能需要同时更新 Vagran…...
嵌入式这个领域会变得过于内卷吗?
今日话题,嵌入式这个领域会变得过于内卷吗?嵌入式开发主要服务于第二产业,尤其是制造业,包括电器、电气、机械、汽车、装备、航空航天等行业的“智能制造”部门,稳定性较强,不像互联网行业那样波动大。因此…...

Linux下安装和使用MySQL的详细教程
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

【Linux】多线程互斥与同步
文章目录 一、线程互斥1. 线程互斥的引出2. 互斥量3. 互斥锁的实现原理 二、可重入和线程安全三、线程和互斥锁的封装1. 线程封装1. 互斥锁封装 四、死锁1. 死锁的概念2. 死锁的四个必要条件3. 避免死锁 五、线程同步1. 线程同步的理解2. 条件变量 一、线程互斥 1. 线程互斥的…...

从零开始:云服务器构建网站的完全指南
目录 一、服务器 二、部署项目 三、购买域名 顶级域名 二级域名 子域名 主机名 四、域名解析 一、服务器 国内华为云、阿里云、腾讯云等看你的选择; 可以选择Linux:CentOS、Ubuntu这些系统版本,更稳定; 服务器控制台&a…...
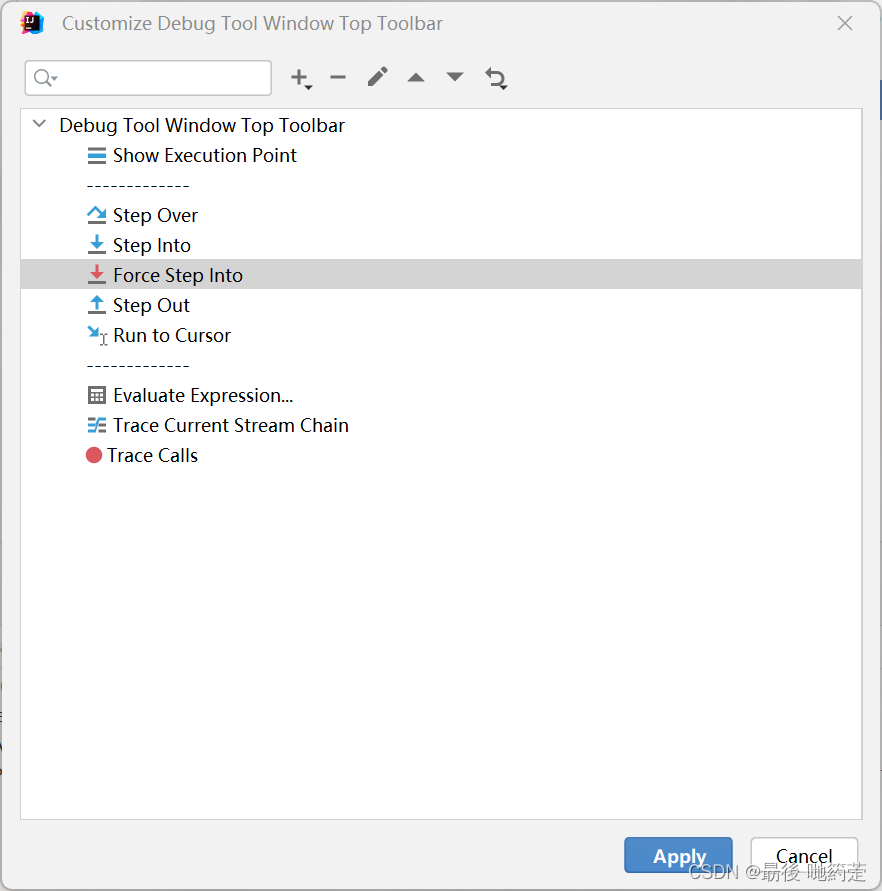
idea中的debug界面上没有进入方法的红色按钮
问题描述: 这里缺少进入系统方法的红色按钮。 问题解决方法: 在上面图片红框范围内右键点击进入。 点击号 搜索 ‘force’ 添加即可完成 上下拖动即可调整界面按钮顺序...
每天10个小知识点)
JavaScript知识系列(4)每天10个小知识点
目录 系列文章目录JavaScript知识系列(1)每天10个小知识点JavaScript知识系列(2)每天10个小知识点JavaScript知识系列(3)每天10个小知识点 知识点**31. Promise** 的概念、作用、原理、特性、优点、缺点、区…...
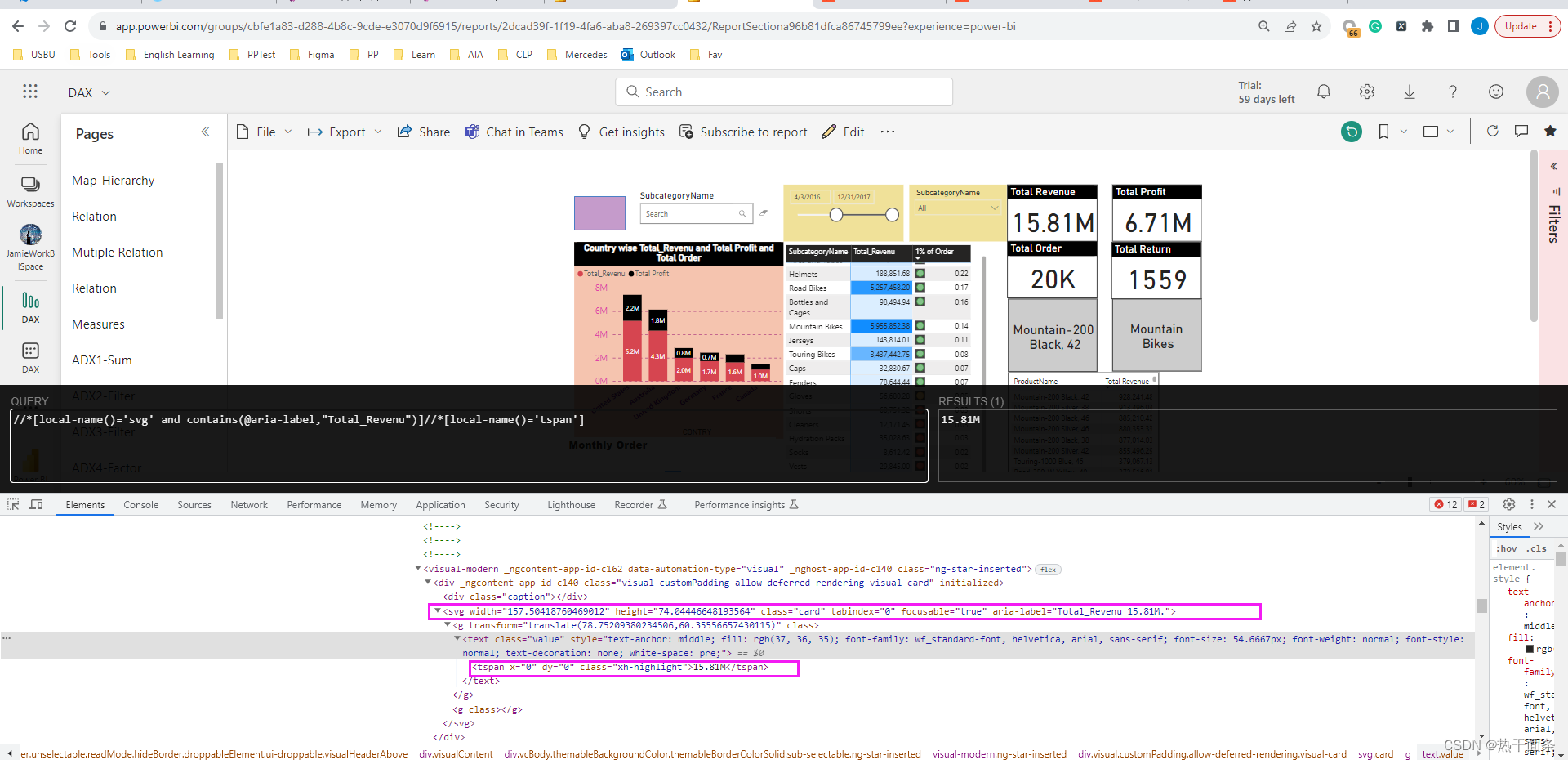
Xpath 访问 Svg 内部的元素
以下是一个例子,获取svg下面的 tspan的元素 //*[local-name()svg and contains(aria-label,"Total_Revenu")]//*[local-name()tspan]...

无涯教程-JavaScript - DOLLARDE函数
描述 DOLLARDE函数将以整数部分和小数部分(如1.02)表示的美元价格转换为以十进制数表示的美元价格。分数美元数字有时用于证券价格。值的小数部分除以您指定的整数。 语法 DOLLARDE (fractional_dollar, fraction)争论 Argument描述Required/OptionalFractional_dollarA nu…...

C语言双向链表
文章目录 前言双向链表链表头结点的创建节点尾插与尾删节点头插与头删特定位置插入或删除节点链表节点查找双向链表的销毁 链表的打印 前言 假期时间因为为学校开学考试做准备所以一直没更新博客,今天开始博客会陆续更新。 双向链表 之前我们说过了顺序表和单链表…...

朋友圈大佬都去读研了,这份备考书单我码住了
作者简介: 辭七七,目前大二,正在学习C/C,Java,Python等 作者主页: 七七的个人主页 文章收录专栏: 七七的闲谈 欢迎大家点赞 👍 收藏 ⭐ 加关注哦!💖…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...
