OpenCV之霍夫变换检测直线
霍夫变换
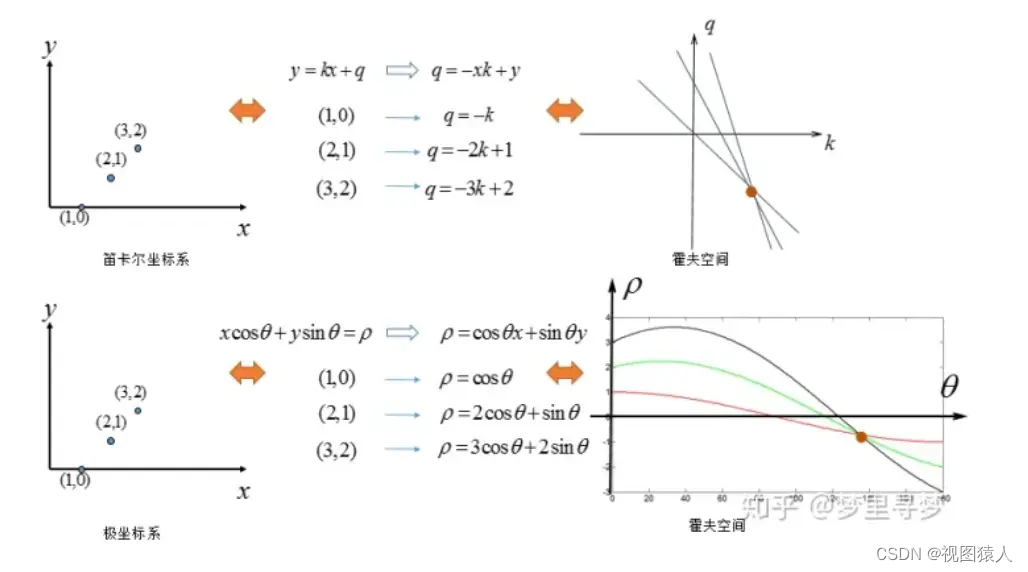
首先是笛卡尔坐标系到霍夫空间的转换,比如笛卡尔坐标系中有一条直线 y=ax+b。
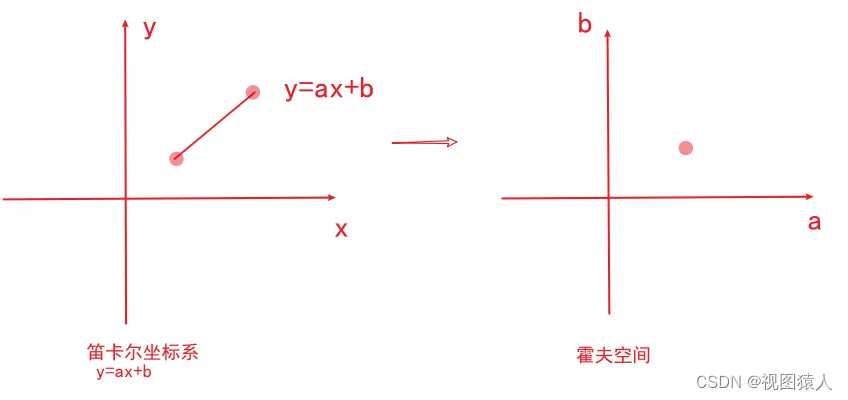
笛卡尔坐标系中一条直线,对应霍夫空间的一个点。
反过来同样成立(霍夫空间的一条直线,对应笛卡尔坐标系的一个点)
原理其实很简单
比如
(1)笛卡尔坐标系内y=ax+b 一条直线确定时 它的斜率和截距是确定的 即是a b是确定的,因此到了霍夫空间内就对应一个(a,b) 即是笛卡尔中一条直线对应霍夫空间一个点
(2)笛卡尔坐标系内一个点 比如x1,y1 相当于x1 y1是确定的 在霍夫空间中
b=-xa+y 即是 b=-x1a+y1 代表的是一条直线 即是笛卡尔中一个点对应霍夫空间一条直线
(3)笛卡尔坐标系多个点
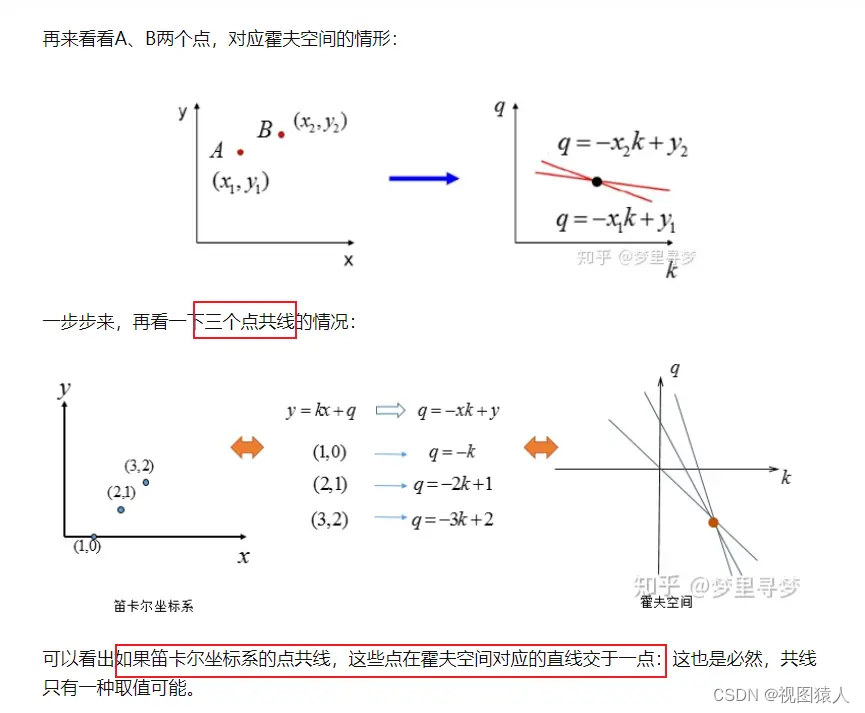
这些点如果共线 就相当于回到了(1) 笛卡尔坐标系中一条直线对应霍夫空间一个点
(4)笛卡尔坐标系多个点 不共线
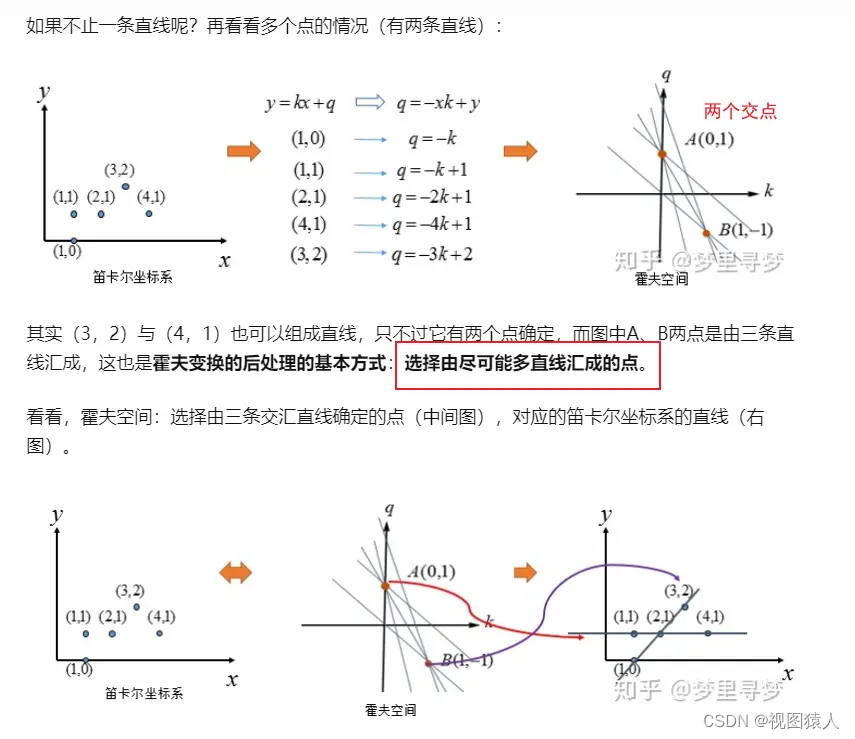
(5)但是 如果直线斜率不存在的时候 霍夫空间那就不容易表示
因此我们换成极坐标 一样的转换原理
先求极坐标方程 其中参数从斜率a和截距b变成 极径p和极角θ
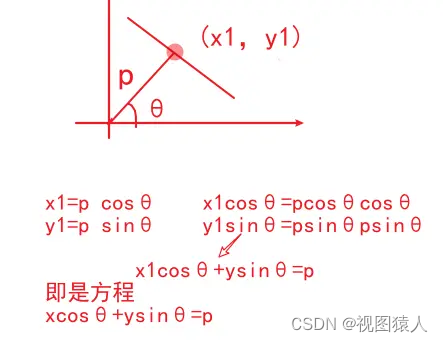
比如下面的变换对比
具体计算过程举例:

OpenCV C++实现
/*
*参数说明:
*src:待检测的原图像
*rho:以像素为单位的距离分辨率,即距离r离散时的单位长度
*theat:以角度为单位的距离分辨率,即角度Θ离散时的单位长度(取值的步长)
*Threshold:累加器阈值,参数空间中离散化后每个方格被通过的累计次数大于该阈值,则该方格代表的直线被视为在原图像中存在
*lines:检测到的直线极坐标描述的系数数组,每条直线由两个参数表示,分别为直线到原点的距离r和原点到直线的垂线与x轴的夹角
*/
void myHoughLines(Mat src, double rho, double theat, int Threshold, vector<Vec2f>& lines)
{if (src.empty() || rho < 0.1 || theat>360 || theat < 0)return;int row = src.rows;int col = src.cols;Mat gray;if (src.channels() > 1){cvtColor(src, gray, COLOR_BGR2GRAY);}elsesrc.copyTo(gray);int maxDistance = sqrt(src.cols * src.cols + src.rows * src.rows); // 图像任意两点最大距离int houghMat_cols = 360 / theat; // theat是角度取值的步长 霍夫变换后距离夹角坐标下对应的Mat的宽(一共多少个θ)int houghMat_rows = maxDistance / rho; // 霍夫坐标距离夹角下对应的Mat的高 就是p的取值个数 Mat houghMat = Mat::zeros(houghMat_rows, houghMat_cols, CV_32FC1); // 存储p和 θ的矩阵//边缘检测Canny(gray, gray, 100, 200, 3);//二值化threshold(gray, gray, 160, 255, THRESH_BINARY);//遍历二值化后的图像for (int i = 0; i < row; i++){for (int j = 0; j < col; j++){if (gray.ptr<uchar>(i)[j] != 0){/*从0到360度遍历角度,得到一组关于距离夹角的离散点,即得到一组关于经过当前点(i,j)按单位角度theat旋转得到的直线*/for (int k = 0; k < 360 / theat; k += theat){// k * CV_PI / 180 是极角 θ double r = i * sin(k * CV_PI / 180) + j * cos(k * CV_PI / 180);// 找哪个(θ,r) 最多 if (r >= 0){ // 直线到原点的距离必须大于0 获得在霍夫变换距离夹角坐标系下对应的Mat的行的下标int r_subscript = r / rho;// 经过该直线的点数加1houghMat.at<float>(r_subscript, k) = houghMat.at<float>(r_subscript, k) + 1;}}}}}/*现在 houghMat 矩阵里面的数值N 是经过这点的线个数(极坐标下)比如说 (行,列)对应 (p, θ) 对应的值就是 经过(p, θ)的线一共N条经过直线的点数N 大于阈值, 则视为在原图中存在该直线 就要这条直线了 */for (int i = 0; i < houghMat_rows; i++){for (int j = 0; j < houghMat_cols; j++){if (houghMat.ptr<float>(i)[j] > Threshold){// line保存直线到原点的距离和直线到坐标原点的垂线和x轴的夹角 求p和θVec2f line(i * rho, j * theat * CV_PI / 180);lines.push_back(line);}}}}相关文章:

OpenCV之霍夫变换检测直线
霍夫变换 首先是笛卡尔坐标系到霍夫空间的转换,比如笛卡尔坐标系中有一条直线 yaxb。 笛卡尔坐标系中一条直线,对应霍夫空间的一个点。 反过来同样成立(霍夫空间的一条直线,对应笛卡尔坐标系的一个点) 原理其实很简单 …...
lv3 嵌入式开发-11 Linux下GDB调试工具
目录 1 GDB简介 2 GDB基本命令 3 GDB调试程序 1 GDB简介 GDB是GNU开源组织发布的一个强大的Linux下的程序调试工具。 一般来说,GDB主要帮助你完成下面四个方面的功能: 1、启动你的程序,可以按照你的自定义的要求随心所欲的运行程序&#…...
Zabbix监控平台概念
1.概念 Zabbix是一款开源的、免费的、分布式监控平台支持web管理,WEB界面可以方便管理员使用可以监控硬件服务器CPU温度、风扇转速、操作系统CPU、EME、DISK、I/O、流量宽带、负载、端口、进程等Zabbix是C/S架构,Client客户端和Server端组成 2.Zabbix可…...
【javaSE】 枚举与枚举的使用
文章目录 🎄枚举的背景及定义⚾枚举特性总结: 🌲枚举的使用🚩switch语句🚩常用方法📌示例一📌示例二 🎍枚举优点缺点🌴枚举和反射🚩枚举是否可以通过反射&…...
NetSuite知识会汇编-管理员篇顾问篇2023
本月初,开学之际,我们发布了《NetSuite知识会汇编-用户篇 2023》,这次发布《NetSuite知识会汇编-管理员篇&顾问篇2023》。本篇挑选了近两年NetSuite知识会中的一些文章,涉及开发、权限、系统管理等较深的内容,共19…...

根号分治与多项式的巧妙结合:GYM-104386G
使用范围:序列上对于每种数的计数问题 考虑对每种数的出现次数进行根号分治 如果出现次数很少,直接平方暴力即可 如果很大考虑任意 ( i , j ) (i,j) (i,j),我们拆一下,再移一下,然后就变成了卷积形式...

通过FTP高速下载几百G数据
基因组下载 (FTP) 常见问题解答 基因组FTP站点有哪些亮点?下载多个基因组组装数据的最简单方法是什么?下载大型数据集的最佳协议是什么?为什么 NCBI 基因组 FTP 站点要重组?我如何及时了解 NCBI 基因组 FTP 站点的变化?...

cudnn-windows-x86_64-8.6.0.163_cuda11-archive 下载
网址不太好访问的话,请从下面我提供的分享下载 Download cuDNN v8.6.0 (October 3rd, 2022), for CUDA 11.x 此资源适配 cuda11.x 将bin和include文件夹里的文件,分别复制到C盘安装CUDA目录的对应文件夹里 安装cuda时自动设置了 CUDA_PATH_V11_8 及path C:\Progra…...
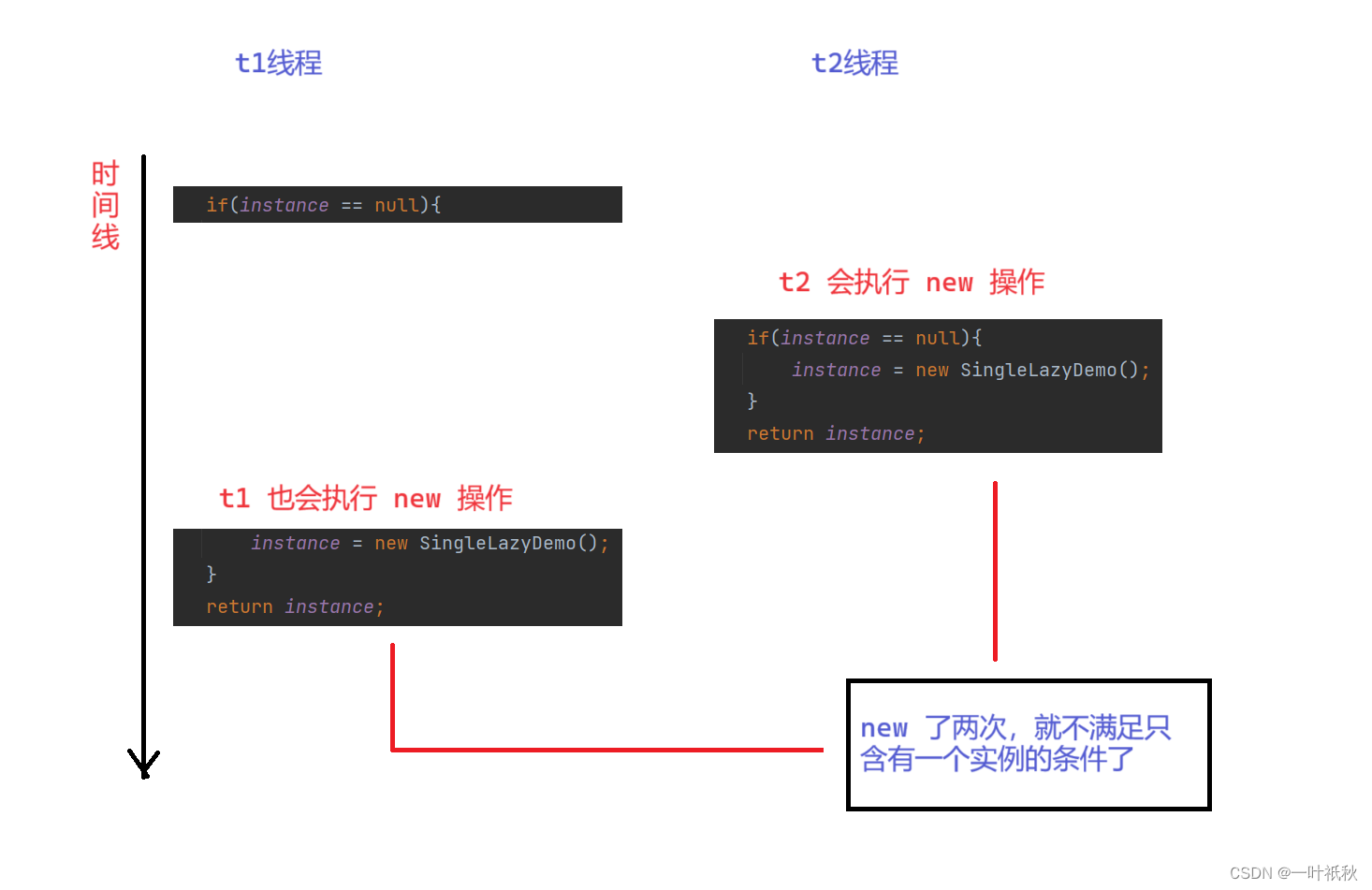
多线程案例(1) - 单例模式
目录 单例模式 饿汉模式 懒汉模式 前言 多线程中有许多非常经典的设计模式(这就类似于围棋的棋谱),这是用来解决我们在开发中遇到很多 "经典场景",简单来说,设计模式就是一份模板,可以套用。…...
)
Arduino驱动TCS34725传感器(颜色传感器篇)
目录 1、传感器特性 2、硬件原理图 3、控制器和传感器连线图 4、驱动程序 TCS34725是一款低成本,高性价比的RGB全彩颜色识别传感器,传感器通过光学感应来识别物体的表面颜色。...
知识库网站如何搭建?需要注意这五个要点!
正因为知识库提供结构化知识库来记载信息和知识,便于团队沉淀经验、共享资源,形成完整的知识体系并持续进化,使得它成为当前企业发展新宠。 构建自己/团队的知识库是一个良好的习惯,可以提高工作和学习效率,以下是一…...

【UE虚幻引擎】UE源码版编译、Andorid配置、打包
首先是要下载源码版的UE,我这里下载的是5.2.1 首先要安装Git 在你准备放代码的文件夹下右键点击Git Bash Here 然后可以直接git clone https://github.com/EpicGames/UnrealEngine 不行的话可以直接去官方的Github上下载Zip压缩包后解压 运行里面的Setup.bat&a…...
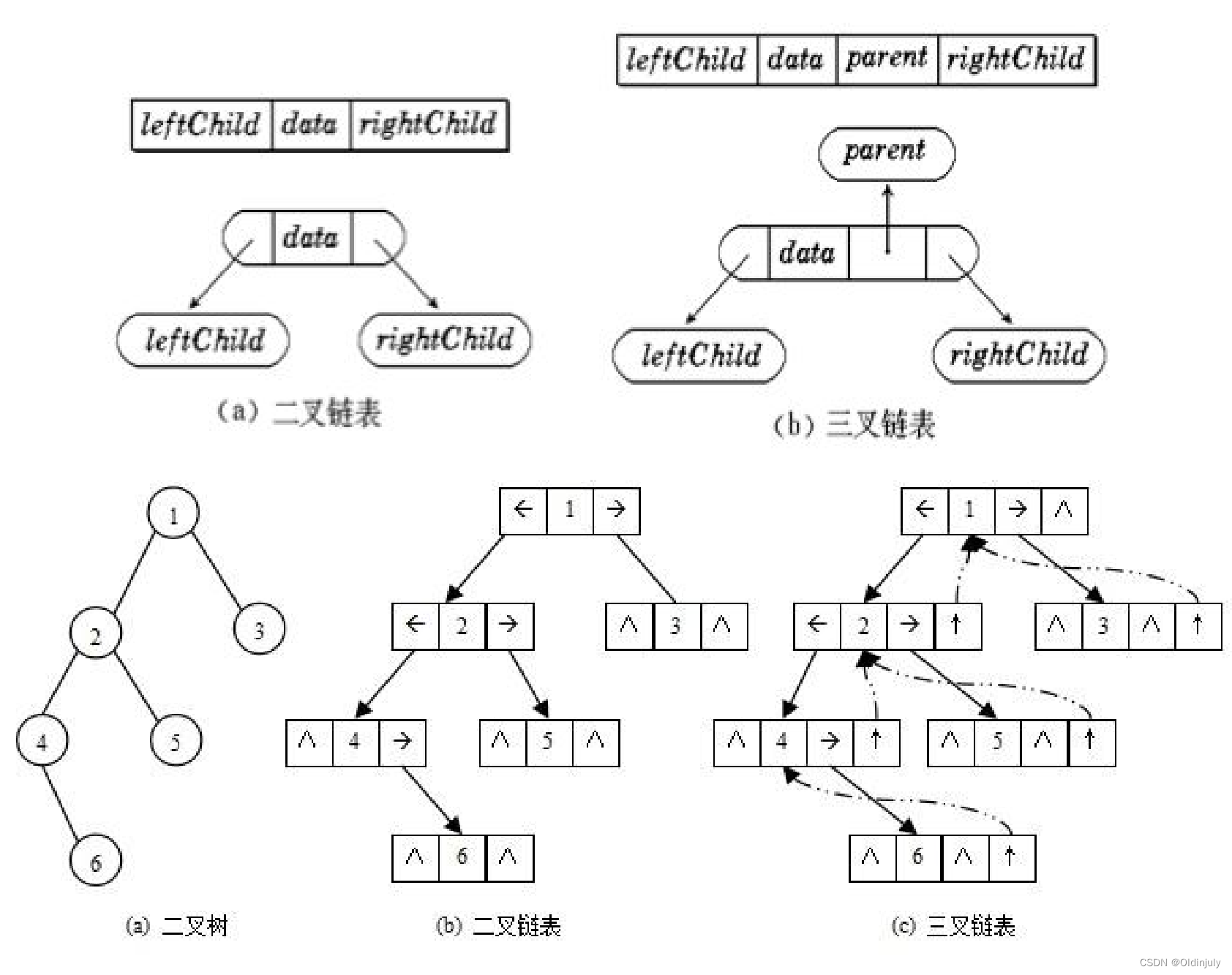
树和二叉树的相关概念及结构
目录 1.树的概念及结构 1.1 树的概念 1.2 树的相关概念 1.3 树的表示 1.3.1 孩子兄弟表示法 1.3.2 双亲表示法 1.4 树的实际应用 2.二叉树的概念及结构 2.1 二叉树的概念 2.2 特殊的二叉树 2.3 二叉树的性质 2.4 二叉树的存储 2.4.1 顺序存储 2.4.2 链式存储 1.树…...
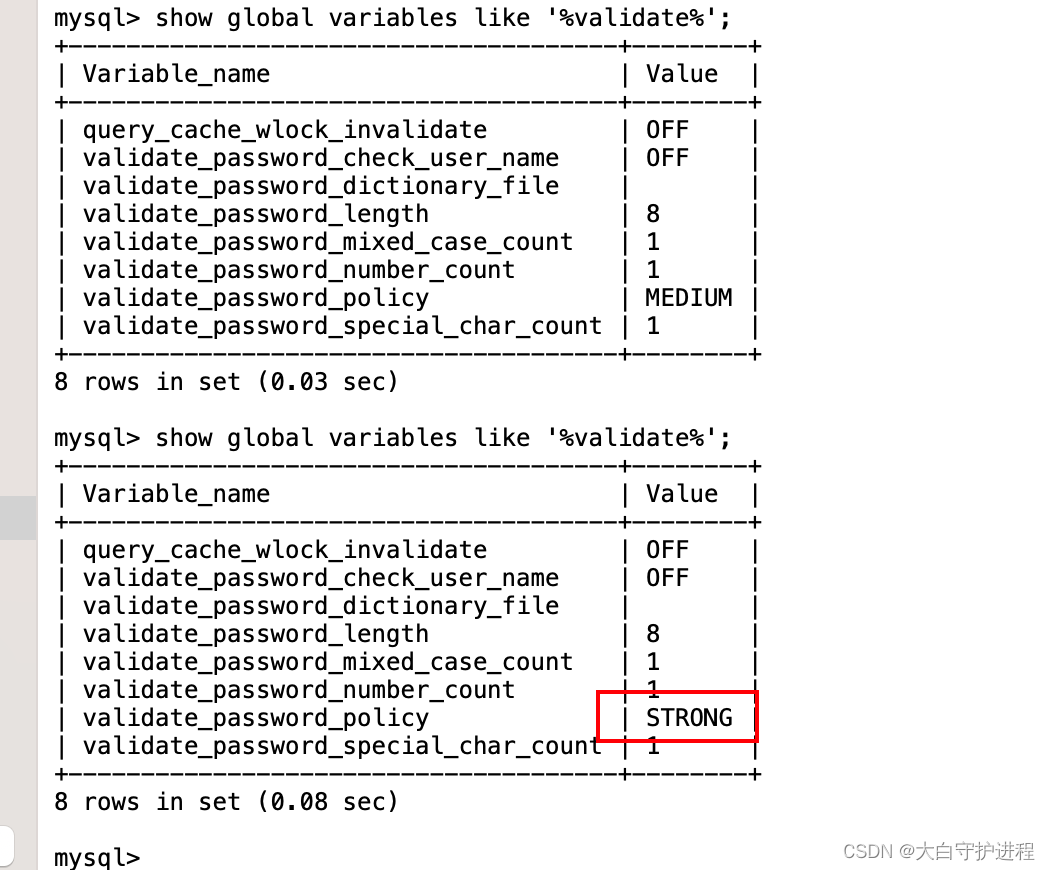
MySQL安装validate_password_policy插件
功能介绍 validate_password_policy 是插件用于验证密码强度的策略。该参数可以设定三种级别:0代表低,1代表中,2代表高。 validate_password_policy 主要影响密码的强度检查级别: 0/LOW:只检查密码长度。 1/MEDIUM&am…...

数据在内存中的存储——练习3
题目: 3.1 #include <stdio.h> int main() {char a -128;printf("%u\n",a);return 0; }3.2 #include <stdio.h> int main() {char a 128;printf("%u\n",a);return 0; }思路分析: 首先二者极其相似%u是无符号格式进行…...

web-案例
分页插件 登录 事务...
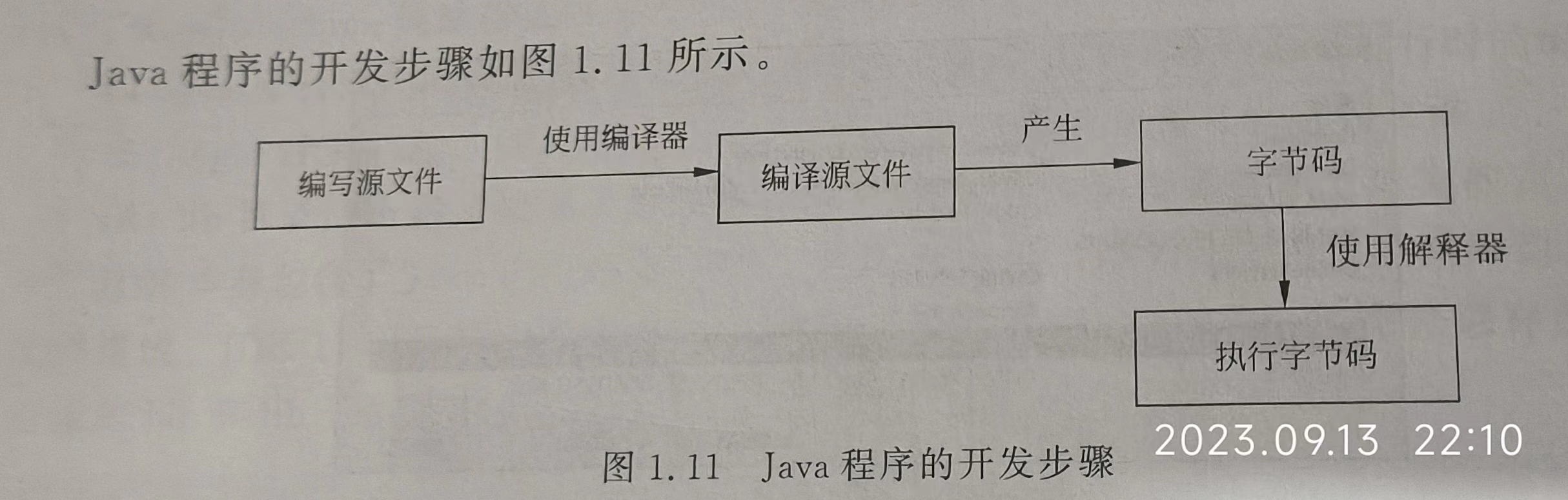
第一章 JAVA入门
文章目录 1.2 Java 的特点1.2.1 简单1.2.2 面向对象1.2.3 与平台无关① 平台与机器指令② C/C程序依赖平台③ Java 虚拟机与字节码1.2.4 多线程1.2.5 动态1.30安装 JDK1.3.1 平台简介0 Java SE②Java EE1.4 Java 程序的开发步骤②保存源文件1.5.2 编译1.8 Java之父-James Gosli…...
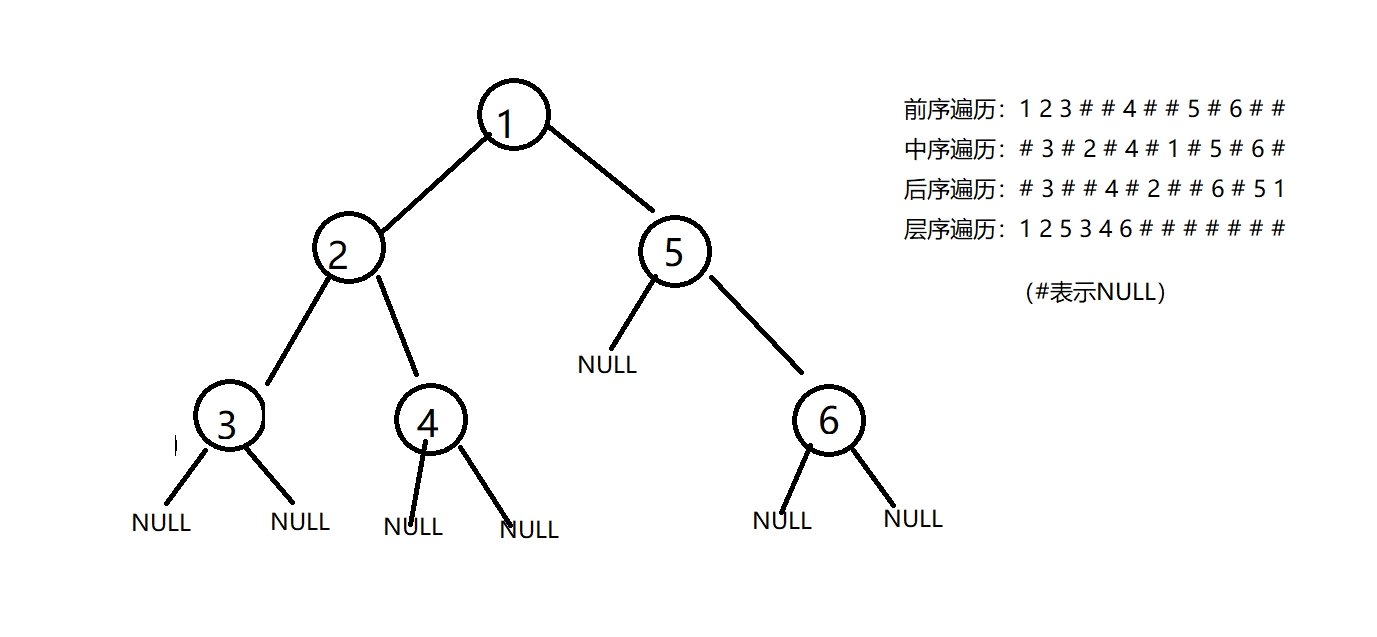
二叉树详解(求二叉树的结点个数、深度、第k层的个数、遍历等)
二叉树,是一种特殊的树,特点是树的度小于等于2(树的度是整个树的结点的度的最大值),由于该特性,构建二叉树的结点只有三个成员,结点的值和指向结点左、右子树的指针。 typedef int DateType; t…...

Apollo配置中心及Python连接
本文将会介绍如何启动Apollo,在Apollo中配置参数,以及如何使用Python连接Apollo. Apollo介绍 在文章Python之读取配置文件和文章Python之配置文件处理中,笔者分别介绍了如何使用Python来处理ini, yaml, conf等配置文件。这种配置方式比较方便…...
--audio - 多媒体音频)
LuatOS-SOC接口文档(air780E)--audio - 多媒体音频
常量 常量 类型 解释 audio.PCM number PCM格式,即原始ADC数据 audio.MORE_DATA number audio.on回调函数传入参数的值,表示底层播放完一段数据,可以传入更多数据 audio.DONE number audio.on回调函数传入参数的值,表示…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
