markdown学习笔记
1.文字(依靠HTML)
1.1文字缩进-空格转义符
单字符空:  半字符空: 
1.2文字对齐
「居中:」<center> 居中 </center> or <p align="center"> 居中 </p>
「左对齐:」<p align="left">左对齐</p>
「右对齐:」<p align="right">右对齐</p>
「居中:」
居中 or居中
「左对齐:」左对齐
「右对齐:」右对齐
1.3 字体与颜色(font=字体)
1.3.1 字体-face
<font face="宋体">字体</font>,
<font face="黑体">字体</font>,
<font face="微软雅黑">字体</font>,
<font face="微软正黑体">字体</font>,
<font face="仿宋">字体</font>,
<font face="楷体">字体</font>,
<font face="仿宋">字体</font>
字体,字体,字体,字体,字体,字体,字体
1.3.2 大小更换-size
Size规定文本的尺寸大小,取值从 1 到 7,浏览器默认值是 3。
<font face="黑体" size=5>我是黑体5号字</font>
我是黑体2号字
1.3.3 颜色-color
<font color=red size=3>红色</font>
红色
1.3.4下划线-u
<u>是非真假无法判断,不如坚强。</u>
是非真假无法判断,不如坚强。
2.表格
2.1 语法格式
| 表头 | 表头 |
| ---- | ---- |
| 单元格 | 单元格 |
| 单元格 | 单元格 |
| 表头 | 表头 |
|---|---|
| 单元格 | 单元格 |
| 单元格 | 单元格 |
2.2 表格对齐
-: 设置内容和标题栏居右对齐。
:- 设置内容和标题栏居左对齐。
:-: 设置内容和标题栏居中对齐。
实例如下:
| 左对齐 | 右对齐 | 居中对齐 |
| :-----| ----: | :----: |
| 单元格 | 单元格 | 单元格 |
| 单元格 | 单元格 | 单元格 |
实例如下:
| 左对齐 | 右对齐 | 居中对齐 |
|---|---|---|
| 傲来雾花果香 | 定海一棒万妖朝 | 东海外水帘中,齐天比高仙折腰 |
| 素衣着泪情诗 | 待你未归人潮逝 | 初相识唇上血,千古第一为红颜 |
3.背景色-如表
<table><tbody><tr><th>颜色名</th><th>十六进制颜色值</th><th>颜色</th></tr><tr><td><font color="AliceBlue">AliceBlue</font></td><td><font color="AliceBlue">F0F8FF</font></td><td bgcolor="AliceBlue">rgb(240, 248, 255)</td></tr><tr><td><font color="AntiqueWhite">AntiqueWhite</font></td><td><font color="AntiqueWhite">#FAEBD7</font></td><td bgcolor="AntiqueWhite">rgb(250, 235, 215)</td></tr><tr><td><font color="Lavender">Lavender</font></td><td><font color="Lavender">#E6E6FA</font></td><td bgcolor="Lavender">rgb(230, 230, 250)</td></tr><tr><td><font color="LavenderBlush">LavenderBlush</font></td><td><font color="LavenderBlush">#FFF0F5</font></td><td bgcolor="LavenderBlush">rgb(255, 240, 245)</td></tr><tr><td><font color=" LightPink"> LightPink</font></td><td><font color=" LightPink">#FFB6C1</font></td><td bgcolor=" LightPink">rgb(255, 182, 193)</td></tr><tr><td><font color="LightSalmon">LightSalmon</font></td><td><font color="LightSalmon">#FFA07A</font></td><td bgcolor="LightSalmon">rgb(255, 160, 122)</td></tr><tr><td><font color="MintCream">MintCream</font></td><td><font color="MintCream">#F5FFFA</font></td><td bgcolor="MintCream">rgb(245, 255, 250)</td></tr><tr><td><font color="MistyRose">MistyRose</font></td><td><font color="MistyRose">#FFE4E1</font></td><td bgcolor="MistyRose">rgb(255, 228, 225)</td></tr><tr><td><font color="Moccasin">Moccasin</font></td><td><font color="Moccasin">#FFE4B5</font></td><td bgcolor="Moccasin">rgb(255, 228, 181)</td></tr><tr><td><font color="MintCream">MintCream</font></td><td><font color="MintCream">#F5FFFA</font></td><td bgcolor="MintCream">rgb(245, 255, 250)</td></tr><tr><td><font color="PaleVioletRed">PaleVioletRed</font></td><td><font color="PaleVioletRed">#D87093</font></td><td bgcolor="PaleVioletRed">rgb(216, 112, 147)</td></tr>
</table>
| 颜色名 | 十六进制颜色值 | 颜色 |
|---|---|---|
| AliceBlue | F0F8FF | rgb(240, 248, 255) |
| AntiqueWhite | #FAEBD7 | rgb(250, 235, 215) |
| Lavender | #E6E6FA | rgb(230, 230, 250) |
| LavenderBlush | #FFF0F5 | rgb(255, 240, 245) |
| LightPink | #FFB6C1 | rgb(255, 182, 193) |
| LightSalmon | #FFA07A | rgb(255, 160, 122) |
| MintCream | #F5FFFA | rgb(245, 255, 250) |
| MistyRose | #FFE4E1 | rgb(255, 228, 225) |
| Moccasin | #FFE4B5 | rgb(255, 228, 181) |
| MintCream | #F5FFFA | rgb(245, 255, 250) |
| PaleVioletRed | #D87093 | rgb(216, 112, 147) |
4.图片
4.1图片大小(依靠HTML)
1.使用zoom
<img src="https://img-blog.csdnimg.cn/img_convert/ef9b0688c1fed69d94b2fd719f1693d3.png" alt="13221564654" style="zoom: 33%;" />
<img src="https://img-blog.csdnimg.cn/img_convert/ef9b0688c1fed69d94b2fd719f1693d3.png" style="zoom: 25%;" />


2.设置style中的width

4.2多张图片并排显示
1.图片连接连着,不空格,不换行



2.居中图片
<center><img src="https://img-blog.csdnimg.cn/img_convert/ef9b0688c1fed69d94b2fd719f1693d3.png" width="100px" /></center>

5.图表
1.顺序图
2.流程图
流程图2
3.饼图
6.数学
1.数学公式
单边大括号: 程序 = { 数据结构 算法 程序=\left\{ \begin{matrix} 数据结构 \\ 算法 \end{matrix} \right. 程序={数据结构算法
程序=\left\{ \begin{matrix} 数据结构 \\ 算法 \end{matrix} \right.
分号:\frac {分子} {分母}
求和符号 y = β 0 + β 1 x + ∑ i = 1 k w i ( x − a i ) + y=\beta_0 +\beta_1 x+\sum_{i=1}^{k}{w_i(x-a_i)_+} y=β0+β1x+i=1∑kwi(x−ai)+
矩阵使用Markdown写矩阵_韩湘的博客-CSDN博客_markdown写矩阵
∏ \prod ∏
相关文章:

markdown学习笔记
markdown学习笔记 1.文字(依靠HTML) 1.1文字缩进-空格转义符 单字符空:  半字符空: 1.2文字对齐 「居中:」<center> 居中 </center> or <p align"center"> 居中 …...

C++项目实战——基于多设计模式下的同步异步日志系统-⑧-日志落地类设计
文章目录 专栏导读抽象基类StdoutSink类设计FileSink类设计RollBySizeSink类设计日志落地工厂类设计日志落地类整理日志落地拓展测试RollByTimeSink类设计测试代码测试完整代码 专栏导读 🌸作者简介:花想云 ,在读本科生一枚,C/C领…...
从零开始探索C语言(八)----指针
文章目录 1. 什么是指针?2. 如何使用指针?3. NULL 指针4. 指针的算术运算5. 指针数组6. 指向指针的指针7. 传递指针给函数8. 从函数返回指针 有人说,指针是C语言的灵魂,所以学习C语言,学习指针是很有必要的。 通过指针…...

SpringMVC 的三种异常处理方式详解
目录 1. 什么是异常 2. 为什么要全局异常处理 3. SpringMVC异常分类 4. 异常处理思路 5. 三种异常处理方式示例 ① 配置 SimpleMappingExceptionResolver 处理器 ② 实现 HandlerExceptionResolver 接口 ③ 使用ControllerAdviceExceptionHandler实现全局异常 6. 响应…...

莫比乌斯召回系统介绍
当前召回系统只能召回相关性高的广告,但不能保证该广告变现能力强。莫比乌斯做了如下两点创新: 在召回阶段,引入CPM等业务指标作为召回依据在召回阶段,引入CTR模型,从而召回更多相关性高且变现能力强的广告 参考 百度…...

使用ASM修改组件化 ARouter
工程目录图 1. apt生成的字节码文件 2. asm 生成的代码 请点击下面工程名称,跳转到代码的仓库页面,将工程 下载下来 Demo Code 里有详细的注释 代码:TestCompont...
第21章_瑞萨MCU零基础入门系列教程之事件链接控制器ELC
本教程基于韦东山百问网出的 DShanMCU-RA6M5开发板 进行编写,需要的同学可以在这里获取: https://item.taobao.com/item.htm?id728461040949 配套资料获取:https://renesas-docs.100ask.net 瑞萨MCU零基础入门系列教程汇总: ht…...

(二十八)大数据实战——Flume数据采集之kafka数据生产与消费集成案例
前言 本节内容我们主要介绍一下flume数据采集和kafka消息中间键的整合。通过flume监听nc端口的数据,将数据发送到kafka消息的first主题中,然后在通过flume消费kafka中的主题消息,将消费到的消息打印到控制台上。集成使用flume作为kafka的生产…...
vue3:22、vue-router的使用
import { createRouter, createWebHistory } from vue-router//history模式:createWebHistory //hash模式:createWebHashHistory//vite中的环境变量 import.meta.env.BASE_URL 就是vite.config.js中的base配置项 const router createRouter({history:…...

深入理解JVM虚拟机第五篇:一些常用的JVM虚拟机(二)
文章目录 一:JRockit VM的介绍 二:J9 VM的介绍 三:KVM和CDC/CLDC Hotspot 四:Azul VM的介绍 五:Liquid VM的介绍 六:Apache Harmoney 七:Microsoft JVM 八:Taobao JVM 九&a…...

导数公式及求导法则
目录 基本初等函数的导数公式 求导法则 有理运算法则 复合函数求导法 隐函数求导法 反函数求导法 参数方程求导法 对数求导法 基本初等函数的导数公式 基本初等函数的导数公式包括: C0(x^n)nx^(n-1)(a^x)a^x*lna(e^x)e^x(loga(x))1/(xlna)(lnx)1/x(sinx)cos…...
SpringMVC系列(六)之JSON数据返回以及异常处理机制
目录 前言 一. JSON概述 二. JSON数据返回 1. 导入pom依赖 2. 添加配置文件(spring-mvc.xml) 3. ResponseBody注解使用 4. 效果展示 5. Jackson介绍 三. 全局异常处理 1. 为什么要全局异常处理 2. 异常处理思路 3. 异常处理方式一 4. 异常处…...
开展汽车消费者焦点小组座谈会调查)
民安智库(北京第三方窗口测评)开展汽车消费者焦点小组座谈会调查
民安智库近日开展了一场汽车消费者焦点小组座谈会,旨在深入了解目标消费者对汽车功能的需求和消费习惯,为汽车企业提供有针对性的解决方案。 在焦点小组座谈会中,民安智库公司(第三方市容环境指数测评)邀请了一群具有…...

【CVPR2021】MVDNet论文阅读分析与总结
Challenge: 现有的目标检测器主要融合激光雷达和相机,通常提供丰富和冗余的视觉信息 利用最先进的成像雷达,其分辨率比RadarNet和LiRaNet中使用的分辨率要细得多,提出了一种有效的深度后期融合方法来结合雷达和激光雷达信号。 MV…...
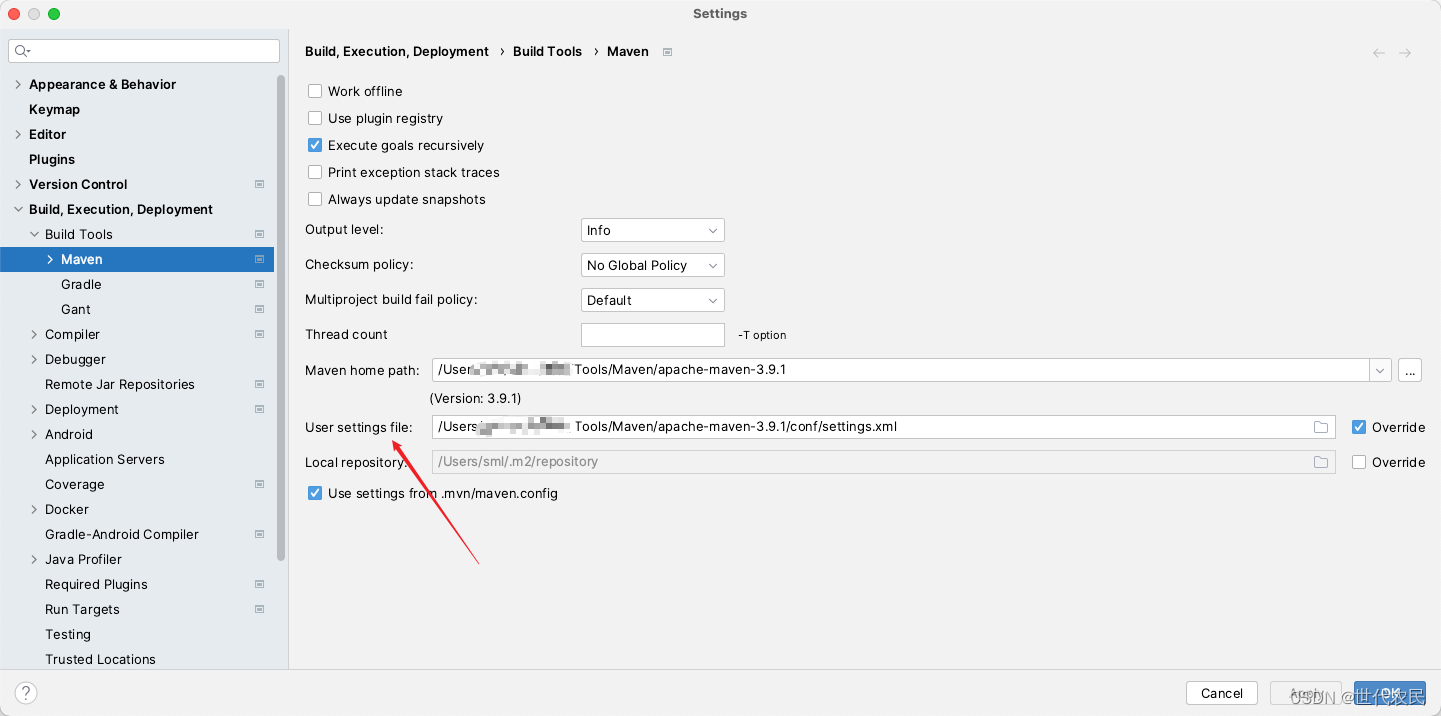
IDEA指定Maven settings file文件未生效
背景:在自己电脑上配置的时候,由于公司项目和我自己的项目的Maven仓库不一致,我就在项目中指定了各自的Maven配置文件。但是我发现公司的项目私有仓库地址IDEA总是识别不到! 俩个配置文件分别是: /Users/sml/Mine/研发…...

swift UI 和UIKIT 如何配合使用
SwiftUI和UIKit可以在同一个iOS应用程序中配合使用。它们是两个不同的用户界面框架,各自有自己的优势和特点。在现实开发中,很多iOS应用程序并不是一开始就完全采用SwiftUI或UIKit,而是根据需要逐步引入SwiftUI或者使用两者共存。 SwiftUI的…...

c语言练习题55:IP 地址⽆效化
IP 地址⽆效化 题⽬描述: 给你⼀个有效的 IPv4 地址 address ,返回这个 IP 地址的⽆效化版本。 所谓⽆效化 IP 地址,其实就是⽤ "[.]" 代替了每个 "."。 • ⽰例 1: 输⼊:address "1.1.1.…...

nvidia-persistenced 常驻
本文地址:blog.lucien.ink/archives/542 发现每次执行 nvidia-smi 都特别慢,发现是需要 nvidia-persistenced 常驻才可以,这个并不会在安装完驱动之后自动配置,需要手动设置一个自启。 cat <<EOF >> /etc/systemd/sy…...
)
leetcode 42, 58, 14(*)
42. Trapping Rain Water 1.暴力解法(未通过) class Solution { public:int trap(vector<int>& height) {int n height.size();int res 0;for(int i0; i<n; i){int r_max 0, l_max 0;for(int j i; j<n; j)r_max max(r_max, heigh…...

SpringCloud-微服务CAP原则
接上文 SpringCloud-Config配置中心 到此部分即微服务的入门。 总的来说,数据存放的节点数越多,分区容忍性就越高,但要复制更新的次数就越多,一致性就越难保证。同时为了保证一致性,更新所有节点数据所需要的时间就…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...
qt+vs Generated File下的moc_和ui_文件丢失导致 error LNK2001
qt 5.9.7 vs2013 qt add-in 2.3.2 起因是添加一个新的控件类,直接把源文件拖进VS的项目里,然后VS卡住十秒,然后编译就报一堆 error LNK2001 一看项目的Generated Files下的moc_和ui_文件丢失了一部分,导致编译的时候找不到了。因…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...
