【管理运筹学】第 7 章 | 图与网络分析(4,最大流问题)
系列文章目录
【管理运筹学】第 7 章 | 图与网络分析(1,图论背景以及基本概念、术语、矩阵表示)
【管理运筹学】第 7 章 | 图与网络分析(2,最小支撑树问题)
【管理运筹学】第 7 章 | 图与网络分析(3,最短路问题)
【管理运筹学】第 7 章 | 图与网络分析(5,最小费用流问题及最小费用最大流问题)
文章目录
- 系列文章目录
- 引言
- 四、最大流问题
- 4.1 有关概念与定理
- 4.1.1 基本概念
- 4.1.2 有关定理
- 4.2 寻找最大流的标号法
- 写在最后
引言
承接系列文章,这一节主要来学习最大流问题。
生活中,有许多流量问题,例如公路系统的车辆流、控制系统的信息流和金融系统的现金流等等。对于这类包含了流量问题的系统,我们往往要在现有系统容量的约束下,求出系统的最大流。
四、最大流问题
4.1 有关概念与定理
4.1.1 基本概念
定义 1 —— 对于网络 G = ( V , A , C ) G=(V,A,C) G=(V,A,C) ,在弧集合 A A A 上的一个函数 f = { f ( v i , v j } f=\{f(v_i,v_j\} f={f(vi,vj} 称为网络流, f ( v i , v j ) f(v_i,v_j) f(vi,vj) 为弧 a i j a_{ij} aij 上的流。 c i j c_{ij} cij 为弧 a i j a_{ij} aij 所能通过的最大流量。
定义 2 —— 满足下列条件的网络流 f f f 称为可行流。
(1)容量限制条件。即每条弧上的流量满足 0 ≤ f ( v i , v j ) ≤ c i j . 0 \leq f(v_i,v_j) \leq c_{ij}. 0≤f(vi,vj)≤cij.
(2)平衡条件。对于中间点,流出量和流入量相等。对于起点,记所有从起点流出的流量,减去流进起点的流量为 V ( f ) V(f) V(f) ;对于终点,所有从终点流出的流量,减去流进终点的流量为 − V ( f ) . -V(f). −V(f).
V ( f ) V(f) V(f) 即为可行流 f f f 的流量,即起点的净输出量或终点的净输入量。
可行流总是存在的,如所有弧的流量 f i j f_{ij} fij 均取 0 ,就是一个可行流, V ( f ) = 0. V(f)=0. V(f)=0.
定义 3 —— 网络中可能会有多条可行流,其中流量最大的可行流我们称为最大流。
设 μ = ( x , ⋯ , u , v , ⋯ , t ) \mu=(x,\cdots,u,v,\cdots,t) μ=(x,⋯,u,v,⋯,t) 是网络 G G G 中的一条初等链(各个顶点均不相同),定义链的方向为 x → t x\to t x→t 。若链上有弧 ( u , v ) (u,v) (u,v) 的方向与 μ \mu μ 的方向一致,称其为前向弧,所有前向弧记为 μ + \mu^+ μ+ 。若链上有弧 ( v , u ) (v,u) (v,u) 的方向与 μ \mu μ 的方向相反,称其为后向弧,所有后向弧记为 μ − \mu^- μ− 。
对于一个可行流 f = { f i j } f=\{f_{ij}\} f={fij} ,我们把网络中使 f i j = c i j f_{ij}=c_{ij} fij=cij 的弧称为饱和弧,使 f i j < c i j f_{ij}<c_{ij} fij<cij 的弧称为非饱和弧,把 f i j = 0 f_{ij}=0 fij=0 的弧称为零流弧, f i j > 0 f_{ij}>0 fij>0 的弧称为非零流弧。
定义 4 —— 设 f f f 为一个可行流, v s v_s vs 是网络起点, v t v_t vt 是网络终点, μ \mu μ 是从起点到终点的一条链,若 μ \mu μ 满足下列条件:
(1)所有前向弧均为非饱和弧。(2)所有后向弧均为非零流。
则称 μ \mu μ 为关于可行流 f f f 的一条增广链。
定义 5 —— 对于有向网络 G = ( V , A , C ) G=(V,A,C) G=(V,A,C) ,若 S S S 为 V V V 的子集, S ‾ = V − S \overline{S}=V-S S=V−S ,则称弧集合 ( S , S ‾ ) = { a ∣ a = ( u , v ) , u ∈ S , v ∈ S ‾ } (S,\overline{S})=\{a|a=(u,v),u\in S,v\in\overline{S}\} (S,S)={a∣a=(u,v),u∈S,v∈S} 为网络 G G G 的一个截集,并将截集中所有弧容量之和称为截容量,简称截量。所有截集中截量最小的称为最小截,其容量为最小截量。
感觉这不就是割集的意思嘛,不过是在有向图中。比如下图,如果 S = { v 2 , v 3 , v 4 , v 5 , v 6 } S=\{v_2,v_3,v_4,v_5,v_6\} S={v2,v3,v4,v5,v6} ,截集为 { ( v 2 , v 1 ) , ( v 3 , v 1 } \{(v_2,v_1),(v_3,v_1\} {(v2,v1),(v3,v1} 。不能加上 ( v 1 , v 4 ) (v_1,v_4) (v1,v4) ,它不是这个截集中的,因为它的起点不在集合 S S S 中。

4.1.2 有关定理
定理 1 —— 若 f ∗ f^* f∗ 是网络 G = ( V , A , C ) G=(V,A,C) G=(V,A,C) 上的可行流,则可行流 f ∗ f^* f∗ 为最大流的充要条件为 G G G 中不存在关于 f ∗ f^* f∗ 的增广链 μ \mu μ 。
定理 2(最大流量、最小截量定理) —— 任一网络 G = ( V , A , C ) G=(V,A,C) G=(V,A,C) 中,从起点 v s v_s vs 到终点 v t v_t vt 的最大流的流量,等于分离 v s v_s vs 与 v t v_t vt 的最小截集的容量。
4.2 寻找最大流的标号法
寻找最大流的标号法,是由 Ford(福特)和 Fulkerson(福克尔逊)首先提出来的,所以又称 2F 算法。
2F 算法可以分为两大过程。首先是标号过程,检查是否存在增广链,如果不存在,现行流就是最大流;否则,进入调整过程,也叫增值过程。标号与调整过程如下。
(1)标号过程
先给起点 v s v_s vs 标上 ( 0 , + ∞ ) (0,+\infty) (0,+∞),不断其它点 v i , v j v_i,v_j vi,vj (包括后向弧),此时有下列两种情况:
- 在前向弧 ( v i , v j ) (v_i,v_j) (vi,vj) 上,若 f i j < c i j f_{ij}<c_{ij} fij<cij ,则给 v j v_j vj 标号 ( v i , l ( v j ) ) (v_i,l(v_j)) (vi,l(vj)) 。其中, l ( v j ) = m i n { l ( v i ) , c i j − f i j } l(v_j)=min\{l(v_i),c_{ij}-f_{ij}\} l(vj)=min{l(vi),cij−fij} 。
- 在后向弧 ( v j , v i ) (v_j,v_i) (vj,vi) 上,若 f j i > 0 f_{ji}>0 fji>0 ,则给 v j v_j vj 标号 ( − v i , l ( v j ) ) (-v_i,l(v_j)) (−vi,l(vj)) 。其中, l ( v j ) = m i n { l ( v i ) , f j i } l(v_j)=min\{l(v_i),f_{ji}\} l(vj)=min{l(vi),fji} 。
重复上述步骤,一旦终点 v t v_t vt 得到标号,表明得到一条增广链,进入调整过程。
若标号过程进行不下去,则算法结束,此时可行流即为最大流。
(2)调整过程
首先根据各点标号进行回溯,找出增广链。增广链的调整量 θ \theta θ 为终点 l ( v t ) l(v_t) l(vt) 。
令 f i j ′ = { f i j + l ( v t ) , ( v i , v j ) ∈ μ + f i j − l ( v t ) , ( v i , v j ) ∈ μ − f i j , e l s e f'_{ij}=\begin{cases} f_{ij}+l(v_t), & (v_i,v_j)\in \mu^+ \\ f_{ij}-l(v_t), & (v_i,v_j)\in \mu^- \\ f_{ij},& else\\ \end{cases} fij′=⎩ ⎨ ⎧fij+l(vt),fij−l(vt),fij,(vi,vj)∈μ+(vi,vj)∈μ−else 即现行流中的前向弧加上调整量,后向弧减去调整量,现行流外的流量不变。
对新流 f i j ′ f_{ij}' fij′ ,重新进行标号过程。
写在最后
最大流问题,相较于之前的最短路还是较为简单些的,不过这只是一个载体,后面结合了最小费用流可就不简单了。
相关文章:

【管理运筹学】第 7 章 | 图与网络分析(4,最大流问题)
系列文章目录 【管理运筹学】第 7 章 | 图与网络分析(1,图论背景以及基本概念、术语、矩阵表示) 【管理运筹学】第 7 章 | 图与网络分析(2,最小支撑树问题) 【管理运筹学】第 7 章 | 图与网络分析…...

linux学习总结
shell 1.在文本环境下,shell作为命令解释器,建立了用户和操作系统之间的接口。当用户键入一个命令时,shell将对该命令进行解释,并调用相应的程序。2.Linux下有多个shell,最常用的3个shell: bash tcsh zsh3.shell …...
【API 管理】什么是 API 管理,为什么它很重要?
当今复杂的数字生态系统由许多相互关联的部分组成。API 作为看门人和连接器在其中发挥着关键作用——提供了许多最终用户甚至没有注意到的自动化机会和效率。 企业密切关注 API。它们对于应用程序、数据和各种客户交互的功能至关重要。 这使得 API 管理成为几乎每个部门的组织…...

基于人体呼出气体的电子鼻系统的设计与实现
基于人体呼出气体的电子鼻系统的设计与实现 摘要 电子鼻技术是通过模式识别技术对传感器采集的人体呼出气体进行分类训练的方法。本文研究实现的电子鼻系统包括下面几个部分:首先搭建以Arduino为控制核心的气路采集装置,包括MOS传感器和双阀储气袋构建的传感器阵列和…...
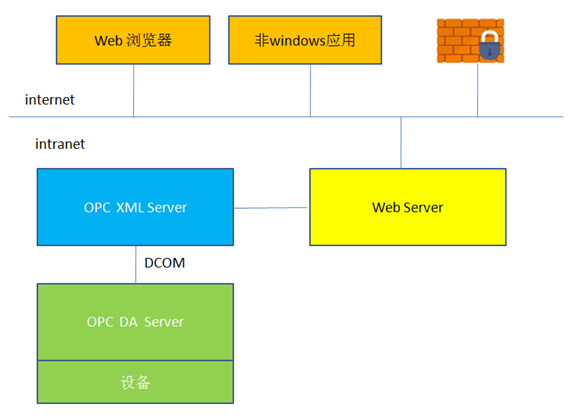
OPC发展历程
目录 1 opc 发展历程 1.1 OPC产生的背景 1.2 经典OPC 1.3 OPC UA 2 OPC DA简介 2.1 OPC Server/Client 2.2 OPC Server 2.3 OPC数据更新 2.4 读取数据方式 3 OPC XML简介 3.1 诞生由来 3.2 功能服务 1 opc 发展历程 OPC是英文“OLE for Process Control”的缩写&am…...
第69步 时间序列建模实战:ARIMA建模(R)
基于WIN10的64位系统演示 一、写在前面 这一期,我们使用R进行SARIMA模型的构建。 同样,这里使用这个数据: 《PLoS One》2015年一篇题目为《Comparison of Two Hybrid Models for Forecasting the Incidence of Hemorrhagic Fever with Re…...

【多线程】CountDownLatch
CountDownLatch 同时等待 N 个任务执行结束. 好像跑步比赛,10个选手进行比赛, 所有选手都通过终点,才能公布成绩。 代码示例: 构造 CountDownLatch 实例, 初始化 10 表示有 10 个任务需要完成.每个任务执行完毕, 都调用 latch.countDown() . 在 Count…...
)
使用 docker buildx 构建跨平台镜像 (QEMU/buildx/build)
目录 1. 使用 buildx 构建跨平台镜像1.1. 简介1.2. 安装1.3. 构建跨平台镜像1.4. 跨平台镜像构建策略1.4.1. 在内核中使用 QEMU 仿真支持1.4.2. 使用相同的构建器实例在多个本机节点上构建。1.4.3. 使用 Dockerfile 中的多阶段构建, 交叉编译到不同的平台架构中。 1.5. 创建 bu…...
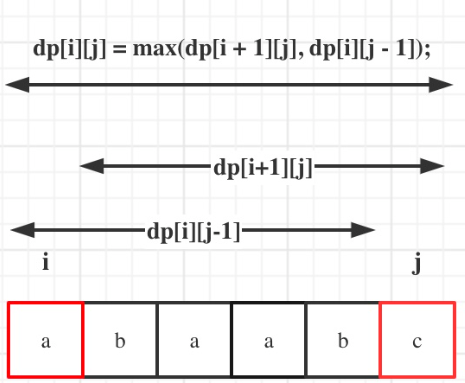
算法|Day49 动态规划17
LeetCode 647- 回文子串 题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目描述:给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子…...

Linux nohup命令
nohup命令 no hang up 在后台启动命令,终端关闭 程序依然可以执行 1.在后台启动命令 命令 nohup COMMAND2.使用nohup命令在后台启动COMMAND, 并将所有标准输出都重定向到fileA nohup COMMAND > /path/fileA 2>&1 &# COMMAND 需要运行的命令 # &g…...
SQL Server 跨库/服务器查询
这里写目录标题 1 SQL Server 跨库/服务器查询1.1 跨库查询1.2 跨服务器查询1.2.1 创建链接服务器1.2.2 跨库查询 1.3 拓展:SQL Server 中所有权和用户与架构的分离 1 SQL Server 跨库/服务器查询 1.1 跨库查询 在同一服务器下的跨库查询较为简单,示例…...
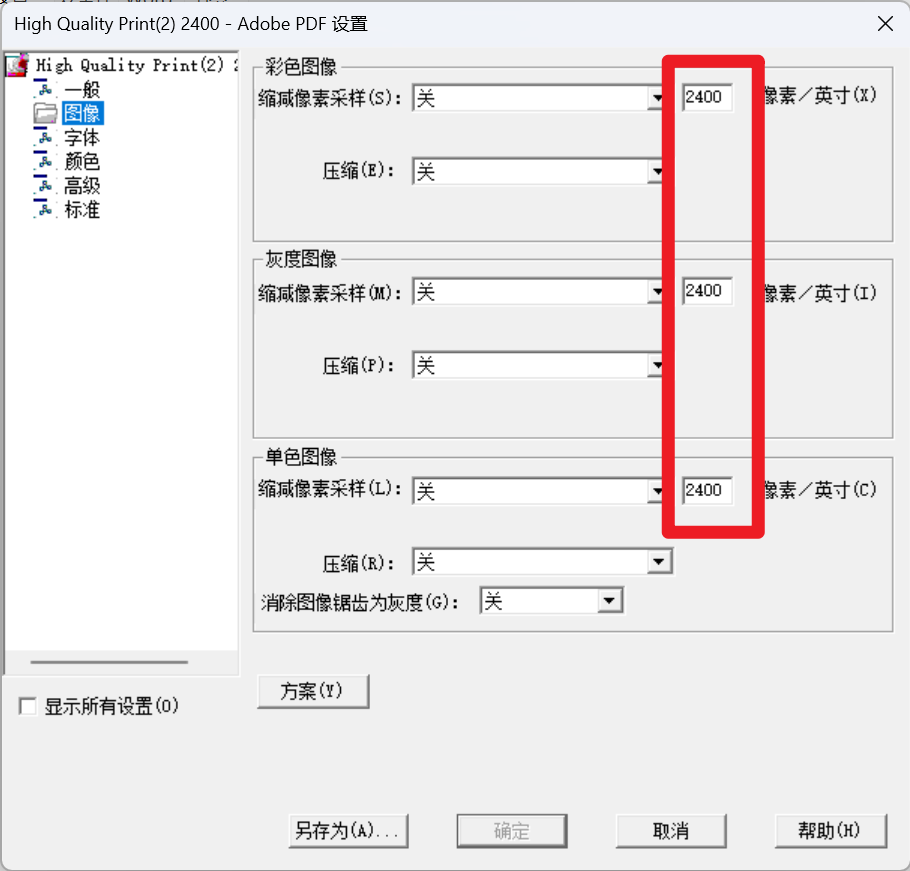
word转PDF文件变小,图片模糊
word论文29M,文件——另存为——只有1.5M左右,图片压缩严重,图片看不清。 word中很多大图,5M一张的图,所以word很大。 找了很多方法,转换后都在2M左右,勉强可以。 直到找到了这个,…...
被删除并且被回收站清空的文件如何找回
文件的意外删除和回收站清空是许多用户面临的普遍问题。这种情况下,很多人会感到无助和焦虑,担心自己的重要文件永远丢失。然而,幸运的是,依然存在一些有效的方法能够帮助我们找回被删除并且被回收站清空的文件。 ▌被删除文件在…...
)
每日两题 131分割回文串 784字母大小写全排列(子集模版)
131 131 题目 给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。 回文串 是正着读和反着读都一样的字符串。 示例 1: 输入:s “aab” 输出:[[“a”,“a”,“b”]…...
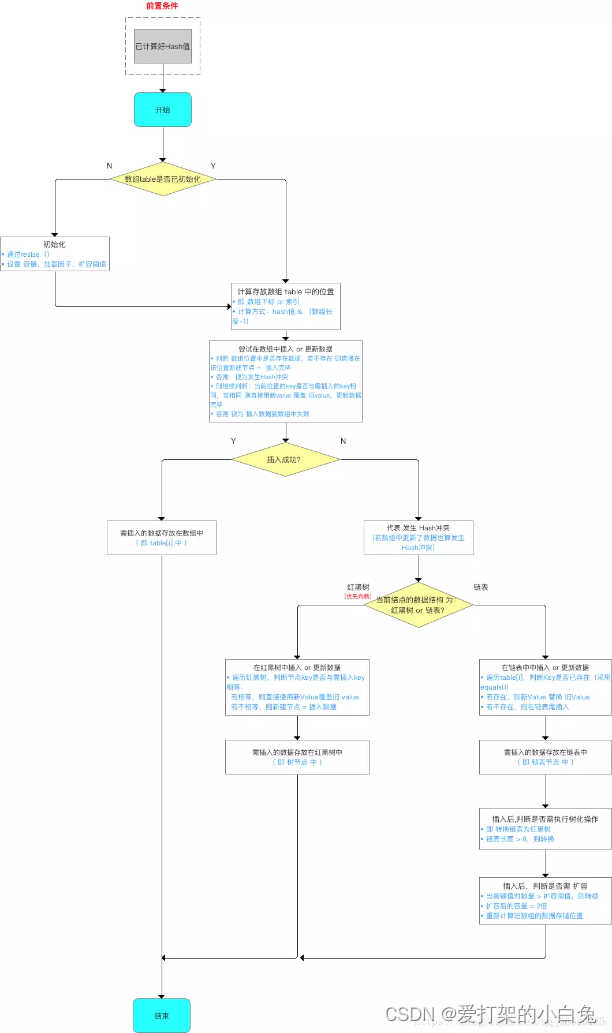
Java面试八股文宝典:初识数据结构-数组的应用扩展之HashMap
前言 除了基本的数组,还有其他高级的数据结构,用于更复杂的数据存储和检索需求。其中,HashMap 是 Java 集合框架中的一部分,用于存储键值对(key-value pairs)。HashMap 允许我们通过键来快速查找和检索值&…...
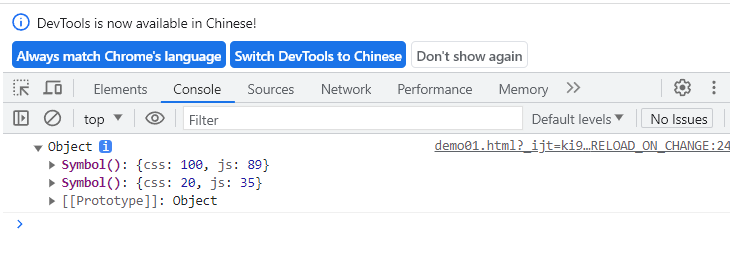
ES6 特性
一、ES6 1.1 ES6 概念 1.1.1 什么是 ES ES 全称 EcmaScript 是脚本语言的规范JavaScript 是 EcmaScript 的一种实现ES 新特性就是指 JavaScript 的新特性 1.1.2 为什么要使用 ES 语法简单,功能丰富框架开发应用前端开发职位要求 1.1.3 为什么要学习 ES6 ES6 …...
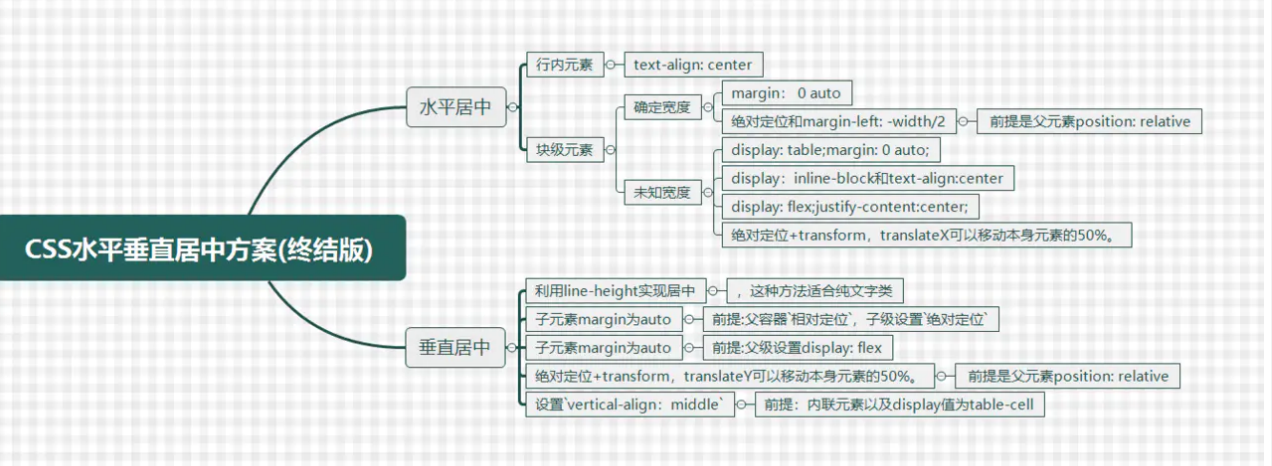
重拾html5
新增的position: sticky; 基于用户的滚动位置来定位,粘性定位的元素是依赖于用户的滚动,在 position:relative 与 position:fixed 定位之间切换。ie15以上的低版本不支持,Safari 需要使用 -webkit- prefix; vertical-align: midd…...
递归学习——记忆化搜索
目录 编辑 一,概念和效果 二,题目 1.斐波那契数 1.题目 2.题目接口 3.解题思路 2.不同的路径 1.题目 2.题目接口 3.解题思路 3.最长增长子序列 1.题目 2.题目接口 3.解题思路 4.猜数字游戏II 1.题目 2.题目接口 3.解题思路 总结&a…...

ChatGPT帮助一名儿童确诊病因,之前17位医生无法确诊
9月13日,Today消息,一位名叫Alex的4岁儿童得了一种浑身疼痛的怪病,每天需要服用Motrin(美林)才能止痛。3年的时间,看了17名医生无法确诊病因。(新闻地址:https://www.today.com/heal…...

Laf 云开发平台及其实现原理
Laf 产品介绍 自我介绍 大家好,我是来自 Laf 团队的王子俊,很高兴今天能在这里给大家分享我们 Laf 云开发平台及其实现原理。本来想说一点什么天气之类的话作为开头,但主持人都说完啦,我就不多说了,还是直接开始今天…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...
