算法通过村第七关-树(递归/二叉树遍历)白银笔记|递归实战
文章目录
- 前言
- 1. 深入理解前中后序遍历
- 从小到大递推
- 分情况讨论,明确结束条件
- 组合出完整的方法:
- 从大到小 画图推演
- 总结
前言
提示:没有客观公正的记忆这回事,所有的记忆都是偏见,都是为自己的存活而重组过的经验。--国强生《断代》
1. 深入理解前中后序遍历
深度优先遍历有前中后序三种情况,大部分人看过后就可以写出来,但是很多人只是记住了代码结构,稍微改变一下就废了。这就是头疼的地方。
我们再从二叉树的角度看递归,每次遇到递归,都是按照前面说的四步骤来写,可以更好的写出正确的递归算法。通过二叉树可以非常方便的理解递归,递归只是处理当前这一层和下一层之间的关系,并不关系下层和下下层之间的关系,就好比护犊子这个词,比护孙子提起来顺口。不常用也不掺和。具体我们再强调一下着四步:
- 从小到大递推
- 分情况讨论,明确结束条件
- 组合出完整方法
- 想验证,则从大到小画图推演
我们接下来就一步一步看看怎么操作:
从小到大递推
我们从一个二叉树为例:
39 2015 6
我们找一个小部分,最小的子树:
20 15 6
假如20为head,则此时前序访问顺序应该是:
public void visit() {list.add(root);// 20被访问root.left; // 继续访问15root.right; // 继续访问7
}
然后再往上看,node(3)的情况:
public void visit() {list.add(root);// 3被访问root.left; // 继续访问9root.right; // 继续访问20
}
这里的20 是一个子树的父节点,访问方式与上面的访问一样,我们就直接把他们合并在一起:
public void visit() {list.add(root);// 20被访问visit(root.left); // 继续访问15visit(root.right); // 继续访问7
}
这就是我们期待的递归方法。
分情况讨论,明确结束条件
上面我们已经总结出了递归的主体,但是这个递归在什么时候结束呢?很明显root == null的时候停驶。一般来说链表和二叉树问题的终止条件都包含当前访问元素为null。有些题目结束条件复杂也是有的,此时最好的方法就是
将可能结束的情况列举出来,然后整理一下就可以了,这个我们接着往下看。
组合出完整的方法:
到目前位置:我们就可以整理出完整的代码,同时为了方便区分,我们将方法名换成perorder:
public void perorder(TreeNode root,List<Integer> res) {if(root == null){return ;}res.add(root.val);perorder(root.left,res); perorder(root.right,res);
}
从大到小 画图推演
写完之后不要觉得就万事大吉了?递归的方法很难调试的,即使对的,你也可能会晕,这里介绍一种简单的验证方法–调用过程图法。我们可以画几个过程图看一看,因为是递归函数,如果比较复杂我们可以少画几组。
递归的特征是“不撞南墙不回头”,一定是在执行到某个root==null才开始返回的,如下图:

从图中可以看到,当root的一个子树为null的时候就不会继续执行递归,进入之后发现root == null,就看是返回了。这里要注意res.add()的时机,将其进入顺序一次写出来就是我们需要的结果。该过程明确之后在debug就很容易,刚开始学习递归我建议多画几次,熟悉之后就不必再画图了。
前序遍历写出来之后,中序和后序遍历就不是很难了,中序是左中右,后序时左右中。代码如下:
// 中序遍历
public void inOrderRecur(TreeNode root,List<Integer> res) {if(root == null){return ;}perorder(root.left,res); Sysytem.out.print(root.val + " ");perorder(root.right,res);
}
// 后续遍历
public void postOrderRecur(TreeNode root,List<Integer> res) {if(root == null){return ;}perorder(root.left,res); perorder(root.right,res); Sysytem.out.print(root.val + " ");
}
另外需要注意的是:
面试和力扣的上面提供的方法可能不能直接用来递归,需要我们在常创建一个方法:
例如:144. 二叉树的前序遍历 - 力扣(LeetCode)

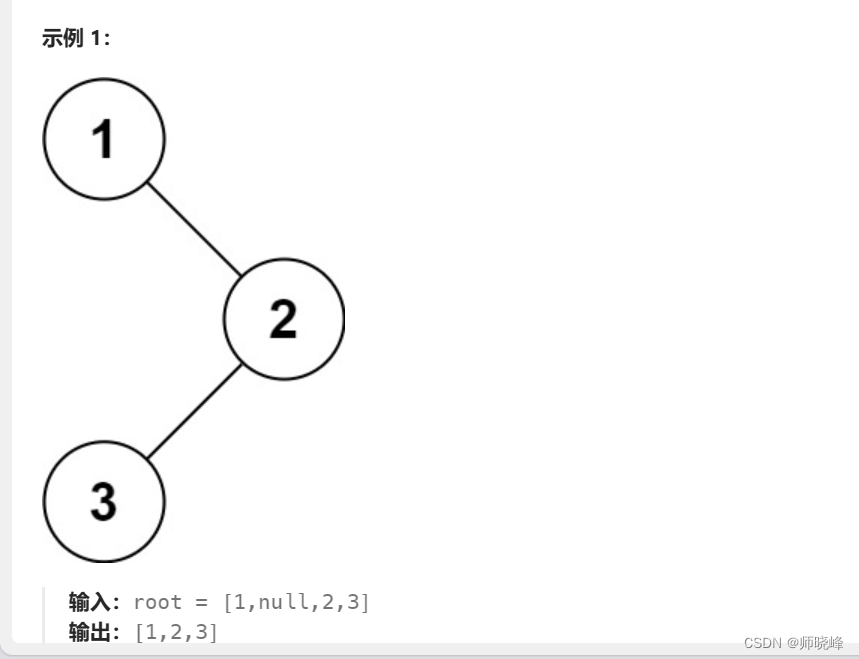
现在看到这个题目就很简单吧🥰:
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>();preorder(root,res);return res;}public static void preorder(TreeNode root, List<Integer> res) {if (root == null) {return;}res.add(root.val);preorder(root.left,res);preorder(root.right,res);}
总结
提示:图解递归;二叉树递归遍历;怎么写好递归
相关文章:

算法通过村第七关-树(递归/二叉树遍历)白银笔记|递归实战
文章目录 前言1. 深入理解前中后序遍历从小到大递推分情况讨论,明确结束条件组合出完整的方法:从大到小 画图推演 总结 前言 提示:没有客观公正的记忆这回事,所有的记忆都是偏见,都是为自己的存活而重组过的经验。--国…...
- 抖音小程序高级功能)
抖音小程序开发教学系列(6)- 抖音小程序高级功能
第六章:抖音小程序高级功能 6.1 抖音小程序的支付功能6.1.1 接入流程6.1.2 注意事项 6.2 抖音小程序的地理位置和地图功能6.2.1 接入流程6.2.2 使用方法 6.3 抖音小程序的实时音视频功能6.3.1 接入流程6.3.2 使用方法 6.4 抖音小程序的小游戏开发6.4.1 基本流程6.4.…...

SpringBoot运行原理
目录 SpringBootApplication ComponentScan SpringBootConfiguration EnableAutoConfiguration 结论 SpringbootApplication(主入口) SpringBootApplication public class SpringbootConfigApplication {public static void main(String[] args) {…...
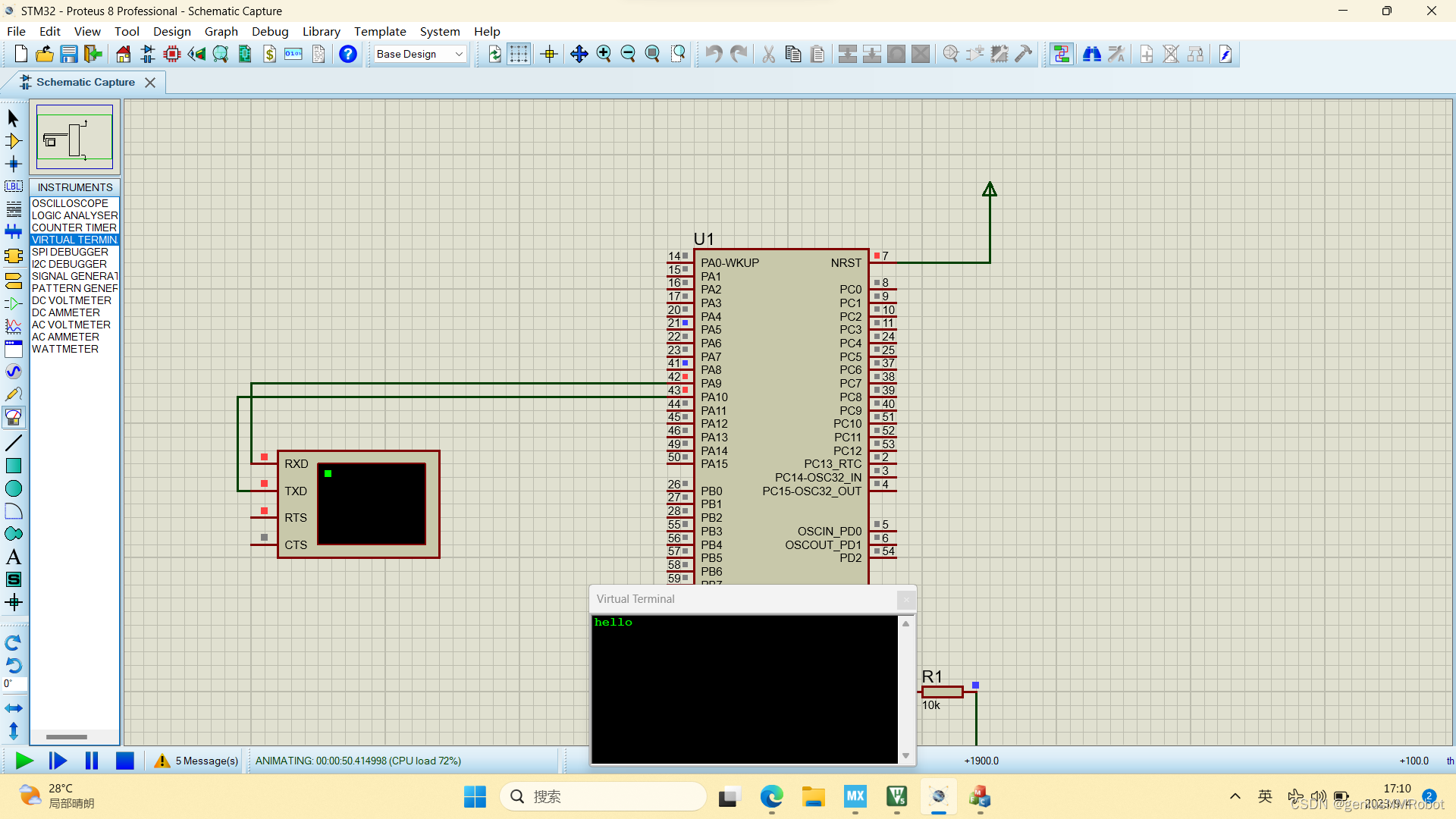
为什么Proteus串口无法正常显示
我以前就可以正常显示,但是最近一段时间,发现串口无法正常显示,试了很多办法都不行, 然后今天干好有点时间就刷了个机,然后居然就好了, 这就说明:Proteus不正常可能是病毒破坏了某个文件导致异…...
Furion api npm web vue混合开发
Furion api npm web vue混合开发 Furion-api项目获取swagger.json文件复制json制作ts包删除非.ts文件上传到npm获取npm包引用 Furion-api项目获取swagger.json文件 使用所有接口合并的配置文件 复制json制作ts包 https://editor.swagger.io 得到 typescript-axios-clien…...
【搭建私人图床】本地PHP搭建简单Imagewheel云图床,在外远程访问
文章目录 1.前言2. Imagewheel网站搭建2.1. Imagewheel下载和安装2.2. Imagewheel网页测试2.3.cpolar的安装和注册 3.本地网页发布3.1.Cpolar临时数据隧道3.2.Cpolar稳定隧道(云端设置)3.3.Cpolar稳定隧道(本地设置) 4.公网访问测…...

BOM操作
文章目录 BOM事件页面加载调整窗口事件定时器停止计时器Location对象History对象Offsetleft获取元素偏移Offset与style的区别可视区client系列滚动scroll系列Mouseover和mousenter区别 动画原理实现动画封装给不同对象添加定时器缓动动画原理多个位置间移动 BOM事件 页面加载 …...

【校招VIP】前端操作系统之存储管理加密
考点介绍 加密算法有很多,如不可逆的摘要算法MD5、SHA(安全哈希算法),可逆的Base64编码,对称加密算法DES、AES,还有非对称加密算法DH、RSA等。那是不是说明我们可以使用任何一种加密算法就能保证网站的安全…...
windows 下载安装 mysql
windows 下载安装 mysql 官网地址:https://dev.mysql.com/ 下载地址:https://cdn.mysql.com//Downloads/MySQLInstaller/mysql-installer-community-8.0.34.0.msi 点击 Downloads 点击 MySQL Community (GPL) Downloads 点击 MySQL Installer for Window…...

第14章_瑞萨MCU零基础入门系列教程之QSPI
本教程基于韦东山百问网出的 DShanMCU-RA6M5开发板 进行编写,需要的同学可以在这里获取: https://item.taobao.com/item.htm?id728461040949 配套资料获取:https://renesas-docs.100ask.net 瑞萨MCU零基础入门系列教程汇总: ht…...

【pygame】01 pygame制作游戏的最小系统
这次使用sublimepython进行pygame的游戏开发,目的是学习使用python的基本操作和常用模块 添加一个文件夹到工程 最小系统 1.导入使用的模块 2.初始化:pygame.init函数包含了各个子模块的初始化,可以重复调用 3.pygame.display.set_mode返…...

(文末赠书)我为什么推荐应该人手一本《人月神话》
能点进来的朋友,说明你肯定是计算机工作的朋友或者对这本书正在仔细琢磨着的朋友。 文章目录 1、人人都会编程的时代,我们如何留存?2、小故事说明项目管理着为什么必看这本书3、如何评价《人月神话:纪念典藏版》4、本书的目录(好…...

回文串 rust解法
输入一个字符串,判断它是否为回文串。 输入字符串保证不含数字0。所谓回文串,就是反转以后和原串相同,如abba和madam。 样例输入: NOTAPALINDROME ISAPALINILAPASI 样例输出: not huiwen huiwen 解法: u…...
持续更新中)
echarts常用参数详解汇总(饼图,柱形图,折线图)持续更新中
常用配置: X/Y轴线的基础设置《通用》 细微的差距只能去官网查看了,基本一致 这里只是做了个汇总方便查看 xAxis/yAxis: {show:false, // 不显示坐标轴线、坐标轴刻度线和坐标轴上的文字axisTick:{// 不显示坐标轴刻度线show:false, alignWithLabel: tru…...
最新ChatGPT网站源码+支持GPT4.0+支持Midjourney绘画+支持国内全AI模型
一、智能创作系统 SparkAi创作系统是基于国外很火的ChatGPT进行开发的Ai智能问答系统。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI创作ChatGPT?小编这里写一个详细图文教程吧&…...

【MySQL】基础SQL语句——库的操作
文章目录 一. 创建数据库1.1 基础语句1.2 字符集和校验规则1.3 校验规则对读取数据的影响 二. 查看数据库三. 修改数据库四. 删除数据库及备份4.1 删除4.2 备份和还原 结束语 一. 创建数据库 1.1 基础语句 最简洁的创建数据库的SQL语句是: create database db_nam…...
基于YOLOv8模型的海洋生物目标检测系统(PyTorch+Pyside6+YOLOv8模型)
摘要:基于YOLOv8模型的海洋生物目标检测系统可用于日常生活中检测与定位海洋生物目标,利用深度学习算法可实现图片、视频、摄像头等方式的目标检测,另外本系统还支持图片、视频等格式的结果可视化与结果导出。本系统采用YOLOv8目标检测算法训…...

华为星闪联盟:引领无线通信技术创新的先锋
星闪(NearLink),是由华为倡导并发起的新一代无线短距通信技术,它从零到一全新设计,是为了满足万物互联时代个性化、多样化的极致、创新体验需求而诞生的。这项技术汇聚了中国300多家头部企业和机构的集体智慧ÿ…...

炒期权的资金门槛是多少 ?
期权是一种合约,买方向卖方支付一定费用后有权利在特定的时间,以特定的价格买入或卖出一定数量的特定资产,卖方需履行相应义务,期权开户支持线上和零门槛开头,下文介绍炒期权的资金门槛是多少 ?本文来自:期…...
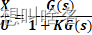
matlab根轨迹绘制
绘制根轨迹目的就是改变系统的闭环极点,使得系统由不稳定变为稳定或者使得稳定的系统变得更加稳定。 在使用PID控制器的时候,首先要确定的参数是Kp,画成框图的形式如下: 也就是想要知道Kp对系统性能有哪些影响,此时就…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...
