MATLAB入门-矩阵的运算
MATLAB入门-矩阵的运算
本篇文章为学习笔记,课程链接为:头歌
相关知识
常见的矩阵运算有算术运算、关系运算和逻辑运算。MATLAB中的所有变量都是以矩阵的形式存储的,单个变量就相当于一个1*1的矩阵。
算术运算
下面展示的是常见的矩阵之间的算术运算:
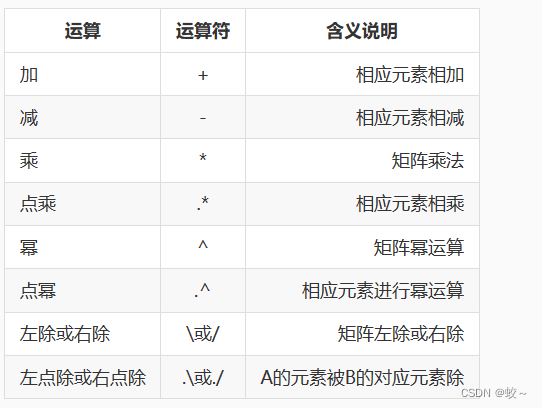
其中矩阵的除运算有两种情况:
- 当两个矩阵同维时:矩阵的除运算表示矩阵相应元素相除;
- 参与运算的矩阵有一个标量时:运算是标量和矩阵的每一个元素相除。左除和右除的关系为a./b=b.\a,其中a是被除数,b是除数。
其中矩阵的点幂运算有两种情况:
- 矩阵的标量乘方:A.^p,其中A为矩阵,p为标量,运算为矩阵每个元素的p次方,计算结果是与A同维的矩阵。
- 标量的矩阵乘方:p.^A表示以p为底,分别以A的元素为指数求幂值,计算结果是与A同维的矩阵。
关系运算
Matlab提供了6种关系运算符:
<、>、<=、>=、==、~=(不等于)
关系运算符的运算法则:
- 当两个标量进行比较时,直接比较两数大小。若关系成立,结果为1,否则为0。
- 当两个维数相等的矩阵进行比较时,其相应位置的元素按标量关系进行比较,并给出结果,形成一个维数与原来相同的0、1矩阵。
- 当一个标量与一个矩阵比较时,该标量与矩阵的各元素进行比较,结果形成一个与矩阵维数相等的0、1矩阵。
逻辑运算
Matlab提供了3种逻辑运算符:
&(与)、|(或)、~(非)
逻辑运算符的运算法则:
- 在逻辑运算中,确认非零元素为真(1),零元素为假(0)。
- 当两个维数相等的矩阵进行比较时,其相应位置的元素按标量关系进行比较,并给出结果,形成一个维数与原来相同的0、1矩阵;
- 当一个标量与一个矩阵比较时,该标量与矩阵的各元素进行比较,结果形成一个与矩阵维数相等的0、1矩阵;
- 算术运算优先级最高,逻辑运算优先级最低。
矩阵的转置及常见函数
矩阵的转置就是将矩阵按照列的顺序在行方向展开,在MATLAB里面,这一个操作用’运算来实现,例如矩阵A的转置为A’。
几种矩阵常用的数据分析函数
- 求向量的最大值和最小值
一个向量X的最大值的函数有两种调用格式,分别是:
(1) y=max(X):返回向量X的最大值存入y,如果X中包含复数元素,则按模取最大值;
(2) [y,I]=max(X):返回向量X的最大值存入y,最大值的序号存入I,如果X中包含复数元素,则按模取最大值。
求向量X的最小值的函数是min(X),用法和max(X)完全相同。 - 求矩阵的最大值和最小值
求矩阵A的最大值的函数有3种调用格式,分别是:
- max(A):返回一个行向量,向量的第i个元素是矩阵A的第i列上的最大值;
- [Y,U]=max(A):返回行向量Y和U,Y向量记录A的每列的最大值,U向量记录每列最大值的行号;
- max(A,[],dim):dim取1或2。dim取1时,该函数和max(A)完全相同;dim取2时,该函数返回一个列向量,其第i个元素是A矩阵的第i行上的最大值。
求最小值的函数是min,其用法和max完全相同。
- 求和与求积
1) sum(X):返回向量X各元素的和。
2) prod(X):返回向量X各元素的乘积。
3) sum(A):返回一个行向量,其第i个元素是A的第i列的元素和。
4) prod(A):返回一个行向量,其第i个元素是A的第i列的元素乘积。
5) sum(A,dim):当dim为1时,该函数等同于sum(A);当dim为2时,返回一个列向量,其第i个元素是A的第i行的各元素之和。
6) prod(A,dim):当dim为1时,该函数等同于prod(A);当dim为2时,返回一个列向量,其第i个元素是A的第i行的各元素乘积。 - 平均值与中值
求数据序列平均值的函数是mean,求数据序列中值的函数是median。两个函数的调用格式为:
1) mean(X):返回向量X的算术平均值。
2) median(X):返回向量X的中值。
3) mean(A):返回一个行向量,其第i个元素是A的第i列的算术平均值。
4) median(A):返回一个行向量,其第i个元素是A的第i列的中值。
5) mean(A,dim):当dim为1时,该函数等同于mean(A);当dim为2时,返回一个列向量,其第i个元素是A的第i行的算术平均值。
6) median(A,dim):当dim为1时,该函数等同于median(A);当dim为2时,返回一个列向量,其第i个元素是A的第i行的中值。 - 求矩阵的维数大小
1) length(X):返回一个值,表示当前矩阵的长度,也就是当前矩阵的最大维数。
2) size(X):返回当前矩阵的维数,如果是二维矩阵,返回两个数[m,n],分别是矩阵的行数和列数,如果是一位矩阵,返回一个数d,表示矩阵的元素个数。
课堂小练
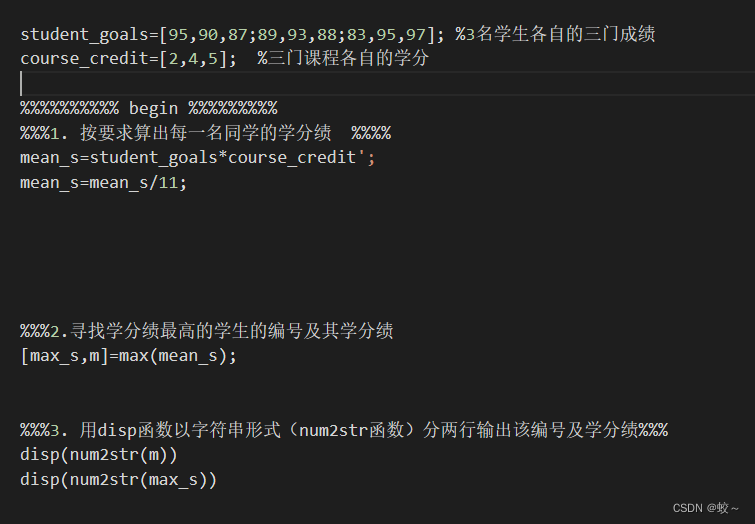
本关任务是对给定的3个学生的三门成绩进行加权平均,算出学分绩,并且输出学分绩最高的同学的编号及学分绩。
- 所谓的学分绩就是将给定的所有门成绩,各自乘上对应的学分,再除以总的学分。例如1号同学的三门成绩分别为90、80和70,三门课程的学分分别为3、2、4,那么学分绩的计算公式为 (90x3+80x2+70x4)/(3+2+4)= 78.89,这就是该同学的学分绩。
相关文章:

MATLAB入门-矩阵的运算
MATLAB入门-矩阵的运算 本篇文章为学习笔记,课程链接为:头歌 相关知识 常见的矩阵运算有算术运算、关系运算和逻辑运算。MATLAB中的所有变量都是以矩阵的形式存储的,单个变量就相当于一个1*1的矩阵。 算术运算 下面展示的是常见的矩阵之…...

[X3m]ros交叉编译
ros需要安装以下包 PYTHON_PACKAGE_LIST"lark lark-parser netifaces pyyaml ifcfg pyunicodedata " TogetheROS.Bot | TogetheROS.Bot用户手册 编译tros.b 1 使用docker文件 该部分操作均在开发机的docker内完成。 ## 创建目录 cd /mnt/data/kairui.wang/…...
【漏洞库】Fastjson_1.2.47_rce
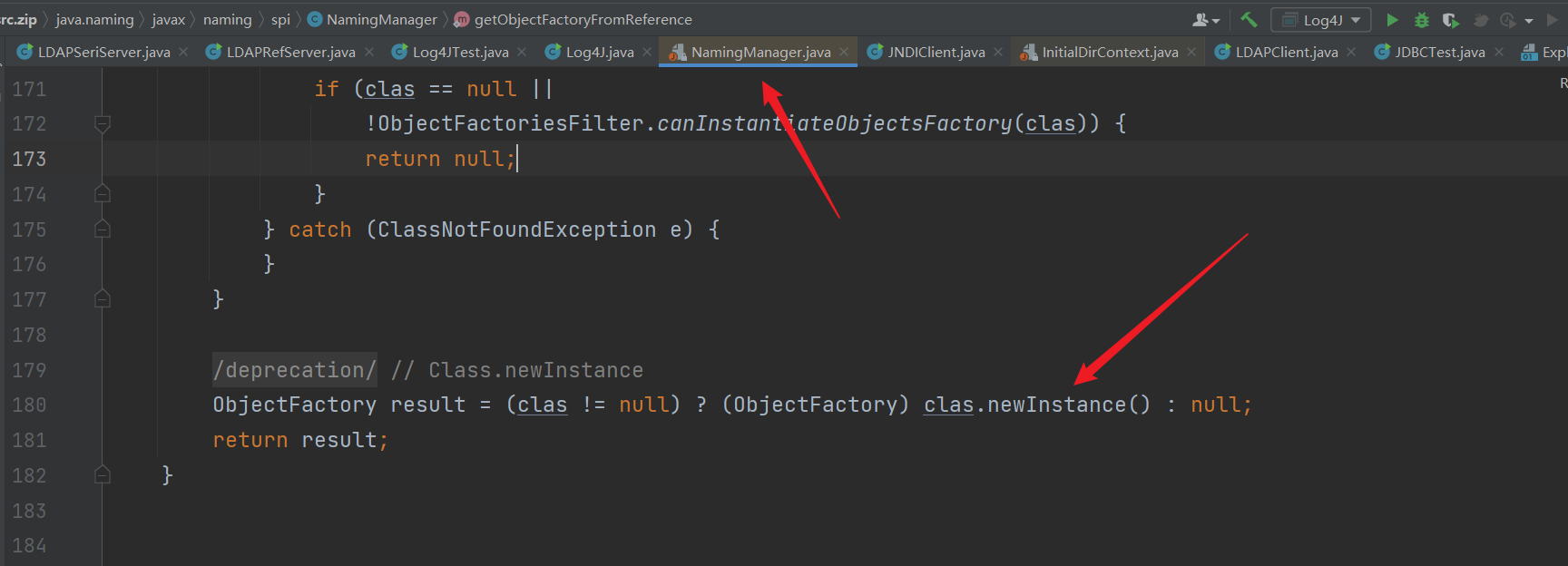
文章目录 漏洞描述漏洞编号漏洞评级影响版本漏洞复现- 利用工具- 漏洞环境- 漏洞扫描- 漏洞验证- 深度利用- GetShell- EXP 编写 漏洞挖掘- 寻找入口点- 指纹信息 修复建议- 漏洞修复 漏洞原理 漏洞描述 Fastjson是阿里巴巴公司开源的一款json解析器,其性能优越&am…...
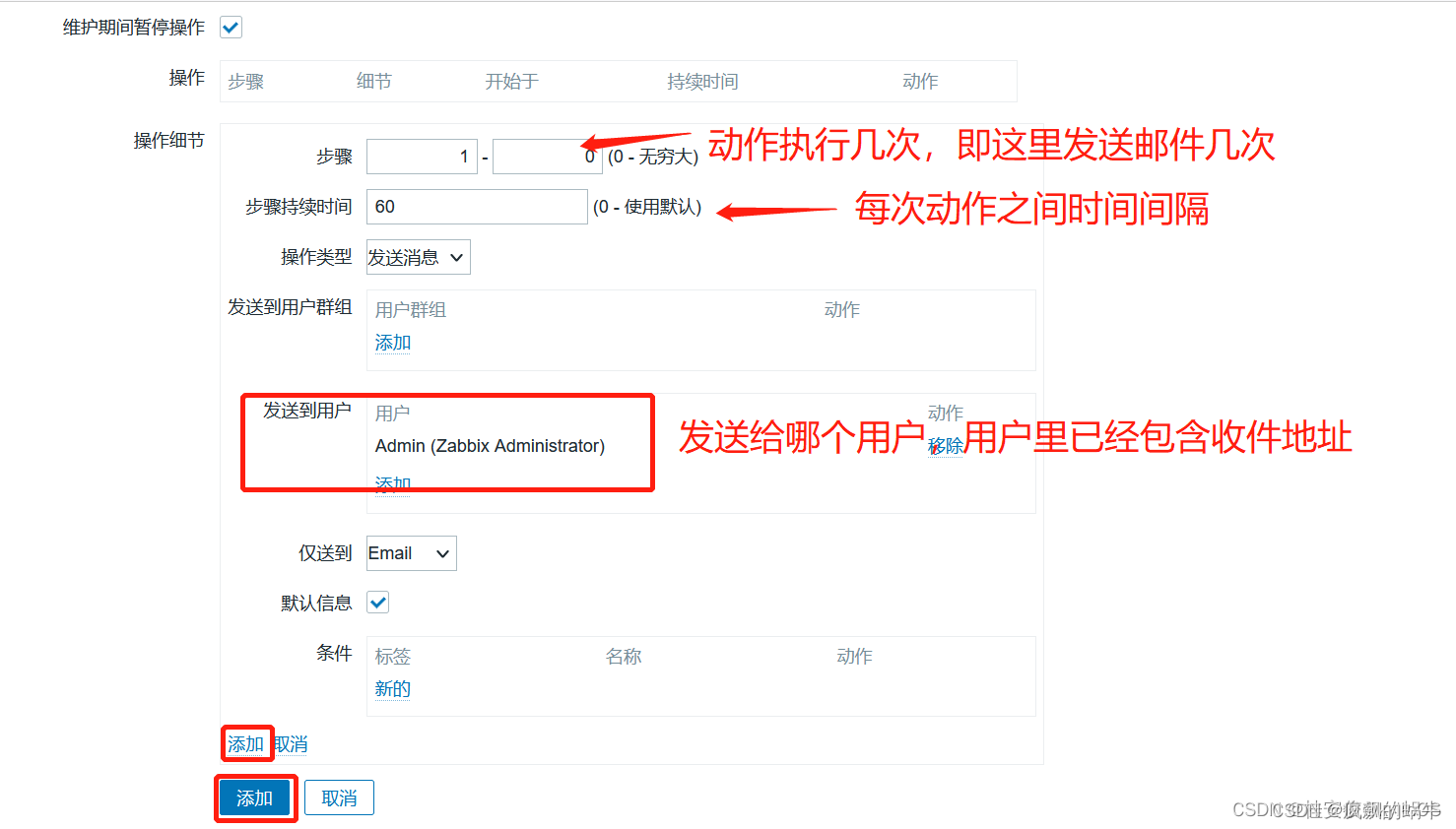
zabbix 钉钉微信企微告警(动作操作消息内容模板)
一、环境配置 1、配置zabbix服务端 2、配置监控主机&监控项&监控模板 zabbix配置安装_this page is used to test the proper operation of _疯飙的蜗牛的博客-CSDN博客 二、触发器 触发器的本质就是一个条件判断,对于不同的监控数据来说,我…...

阿里云国际站云服务器数据备份方法有哪些?
阿里云国际站云服务器是一种根据云计算技术的虚拟服务器,它能够经过互联网提供计算资源和服务。在运用云服务器的过程中,数据备份是非常重要的一个环节。本文将介绍云服务器数据备份的办法,包含手动备份、主动备份和数据同步。 一、手动备份 …...

游戏笔记本电脑可以进行 3D 建模和渲染吗?有哪些优势与缺点?
3D 建模和渲染是创建令人惊叹的数字艺术、动画和游戏体验的最流行和最广泛使用的工具之一。随着技术的进步,对运行这些模型的强大计算机的需求呈指数级增长。对于那些寻求强大机器来处理 3D 建模任务的人来说,游戏笔记本电脑已成为一个可行的选择。 游戏…...

【AI】推理系统和推理引擎的整体架构
本文主要是对 B 站 Up 主 ZOMI酱 推理系统系列视频 的理解,可以认为是重点笔记。 一、深度学习模型的全生命周期 相信很多人和我一样,刚看到深度学习模型中的推理系统或推理引擎时是一头雾水,因为学习 DL 时通常关注于模型的设计和训练。下图…...

k8s集群中流水线部署微服务
k8s集群中流水线发布微服务 一、流水线部署微服务部署流程 二、微服务发布流程 pipeline {agent {node {label maven}}parameters {string(name: PROJECT_VERSION, defaultValue: v1.0, description: )string(name: PROJECT_NAME, defaultValue: , description: )}environment…...

Socks5代理与网络安全:保护您的隐私与数据
在今天数字化的世界中,隐私和网络安全已经成为至关重要的话题。Socks5代理作为一种强大的工具,不仅为用户提供了隐私保护,还在网络安全和爬虫领域发挥着关键作用。本文将深入探讨Socks5代理的工作原理、其在网络安全中的应用,以及…...

2024年山东高企申报注意事项
1、分析企业技术及财务报表 分析财务数据及企业主营产品和技术点。用以确定申报材料的撰写方向。一般耗时1周左右。(纺织厂、服装厂等传统行业面临申报中的面临研发人员比例不达标,研发费用不达标,高新技术产品比例不达标等难题。)…...
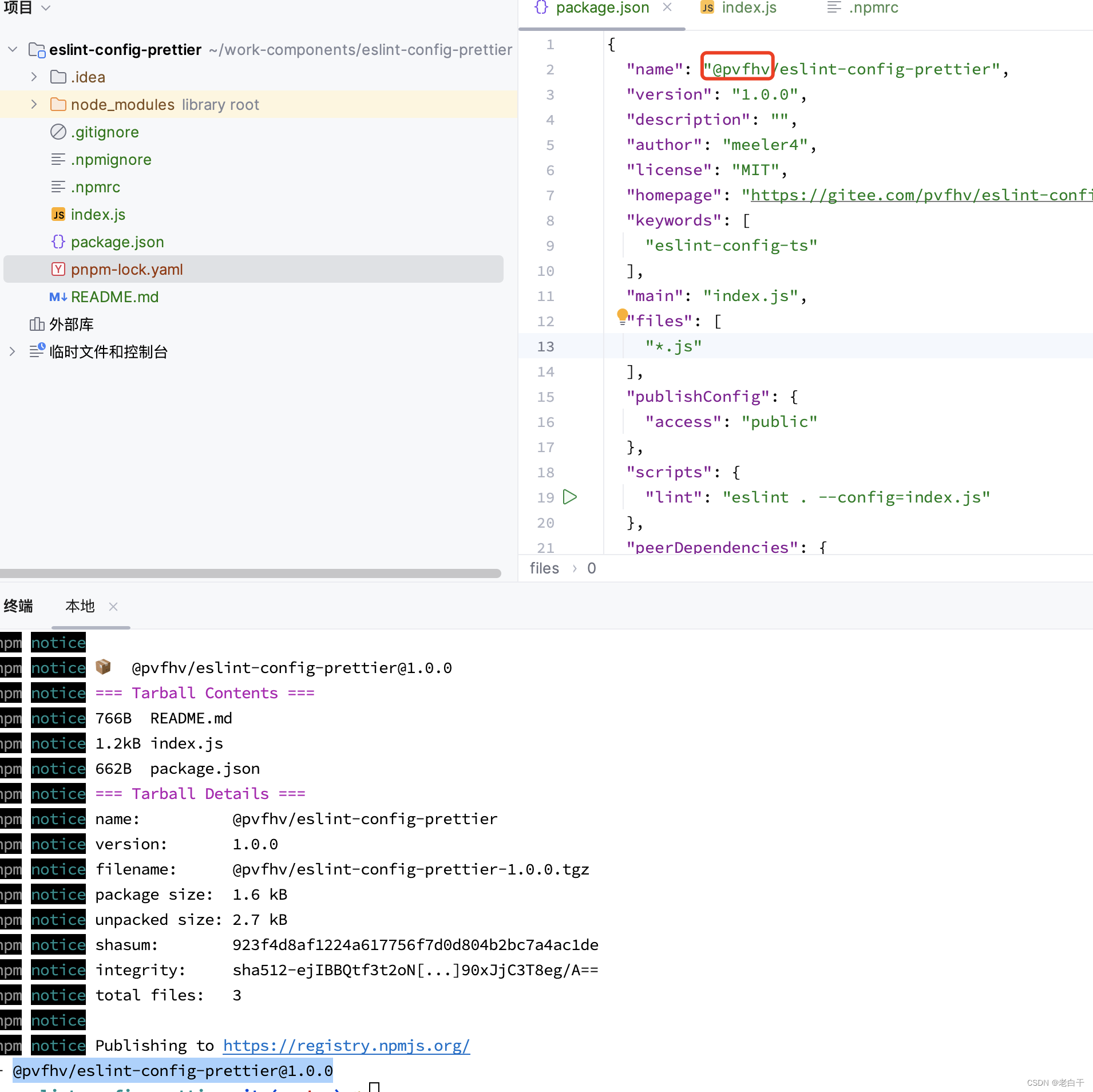
npm publish包报404,is not in the npm registry错误
1. 指定发布目标2. 登录npm,使用登录名发布包,包名命名原则“登录名/包名”,或 “包名” 3. 删除某一个版本npm unpublish pvfhv/eslint-config-prettier1.0.1 --force 删除后的版本不能重复使用,正式解释: Unfortun…...

pytest-基础
一.使用pytest,默认的测试用例的规则以及基础应用 1.模块名字必须已test_开头或者_test结尾 2.测试类必须以Test开头,并且不能有init方法 3.测试方法必须以test开头 示例代码 test_001.py import pytest class TestCase:def test_case(self):print("执行测试用例&quo…...

在openSUSE上开启护眼模式
色温 色温是用来衡量光源色彩时所用到的一个概念,单位为开尔文。热黑体辐射体与光源温度相同时的温度,就是该光源的色温。 显而易见,色温越低时,光源看起来越黄;色温越高时,光源看起来越蓝。下面是一些常见…...
vue基础知识十:Vue中组件和插件有什么区别?
一、组件是什么 回顾以前对组件的定义: 组件就是把图形、非图形的各种逻辑均抽象为一个统一的概念(组件)来实现开发的模式,在Vue中每一个.vue文件都可以视为一个组件 组件的优势 降低整个系统的耦合度,在保持接口不…...

Arthas是一个Java诊断工具 的入门使用
Arthas是一个Java诊断工具,可以帮助开发人员在运行时快速诊断和解决线上应用故障。 以下是Arthas的入门步骤: 安装Arthas 你可以在Arthas Github页面中找到安装指南,根据操作系统选择相应的安装方式。 启动Arthas 在安装完成后ÿ…...

数据结构——排序算法——桶排序
桶排序的思想是: 1.将区间划分为 n 个相同大小的子区间,每个子区间称为一个桶 2.遍历数组,将每个数字装入桶中 3.对每个桶内的数字单独排序,这里需要采用其他排序算法,如插入、归并、快排等 4.最后按照顺序将所有桶内的…...

Kafka消息发送可靠性分析
Apache Kafka是一种高吞吐量的分布式发布订阅消息系统,它可以处理消费者和生产者之间的所有实时数据。Kafka的主要特性包括:高吞吐量、可扩展性、持久性、分布式、可容错等。这些特性使得Kafka成为大规模数据处理和实时数据分析的理想选择。然而…...

如何将一个字符串转换为驼峰命名法(camel case)?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 思路⭐ 示例⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领…...

牛客网项目-第一章-笔记
牛客网项目-第一章 环境配置 java maven idea Spring Intializr 搜索jar包的网站:https://mvnrepository.com/ https://start.spring.io/ 缺少的aop包,手动在pom.xml中加入依赖 <dependency><groupId>org.springframework.boot</gro…...

CISP汇总
0x00 前言 CTF 加解密合集CTF Web合集网络安全知识库溯源相关 文中工具皆可关注 皓月当空w 公众号 发送关键字 工具 获取 本文用来整理相关CISP知识笔记 0x01 汇总...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...
