基于python解决鸡兔同笼问题
一、什么是鸡兔同笼问题?
鸡兔同笼问题是一个经典的数学问题。问题描述:鸡和兔子共有头数a和脚数b,求鸡和兔子的数量。
解析:设鸡的数量为x,兔子的数量为y,那么可以得到以下两个方程:
可以通过解这个二元一次方程组来求解鸡和兔子的数量。
二、Python程序
def chicken_and_rabbit(a, b):for x in range(a + 1):y = a - xif 2 * x + 4 * y == b:return x, yreturn None# 输入头数
a=10;
#输入脚数
b=20;
result = chicken_and_rabbit(a, b)
if result:print("鸡的数量为:", result[0], "兔子的数量为:", result[1])
else:print("无解")
如果没有python运行环境,可以使用在线python编辑器。
在线python编辑器 ——https://c.runoob.com/compile/9/
左边输入程序,点击运行,右侧输出结果。
三、示例
示例1:10头,20脚

示例2:10头,40脚
示例3:7头,22脚
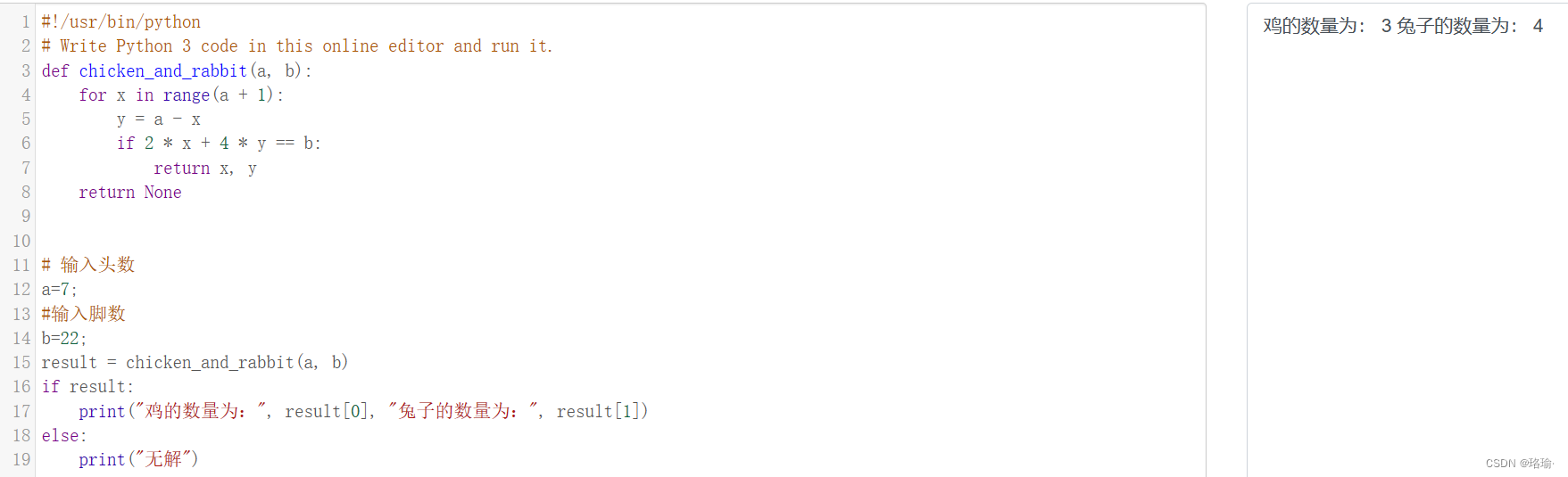
示例4:7头,23脚

相关文章:

基于python解决鸡兔同笼问题
一、什么是鸡兔同笼问题? 鸡兔同笼问题是一个经典的数学问题。问题描述:鸡和兔子共有头数a和脚数b,求鸡和兔子的数量。 解析:设鸡的数量为x,兔子的数量为y,那么可以得到以下两个方程: 1. x y…...

2023 Google 开发者大会|Mobile开发专题追踪
文章目录 前言大会介绍涉及内容MobileWebAICloud Mobile开发专题多终端应用的开发适配大屏视频流可穿戴设备电视新的设计中心 构建高质量的应用高级相机和媒体功能用户的安全和隐私更精细的视觉体验 小结 前言 哈喽大家好,我是阿Q。近期,【2023 Google …...

最新版WPS 2023 加载Zotero方法
安装wps2019vba.exe,获取链接:链接:https://pan.baidu.com/s/1eeoc6Tmwyzxh3n1MFQTVeA 提取码:6431 –来自百度网盘超级会员V8的分享 打开WPS的工具的加载项 添加文件路径,我的在: C:\Users\Administrat…...

详解爬虫策略,反爬虫策略,反反爬爬虫策略
爬虫策略 爬取策略是网络爬虫在执行网页抓取任务时所遵循的规则或策略。这些策略决定了爬虫如何从一个页面转到另一个页面,什么时间进行抓取,以及应该抓取哪些内容。以下是几种常见的爬取策略: 深度优先搜索(DFS) 在…...

ES6中的Promise对象
1. Promise是什么 Promise简单来说就是一个容器,里面保存着未来才会结束的事件的结果(这个事件就是异步操作)。Promise是一个对象(构造函数),可以获取异步操作的结果。 特点: 对象的状态不受外…...

vue 知识点———— 生命周期
1.什么是生命周期 Vue实例从创建到销毁的过程,叫生命周期。 从开始创建、初始化数据、编译模版、挂载Dom-渲染、更新-渲染、销毁等过程。 2.生命周期一共有几个阶段 创建前/后, 载入前/后,更新前/后,销毁前/销毁后 3.初始化相关属性 beforeCreate(创建前…...
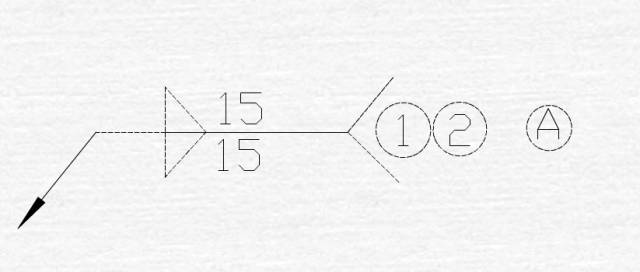
焊接符号学习
欧美焊接符号举例 4.5------表示焊点直径 【3】------根据图示说明,表示此项为CC项或者SC项 6-------表示此处为第六CC项或者SC项 BETWEEN①AND②------表示①件和②件俩点之间的焊点 12X------表示俩点之间的焊点个数为12个 日本焊接符号举例 A------根据图示&…...

记录linux清理空间的步骤
sudo du -sh /* 看整体空间占用情况 [roothost ~]# sudo du -sh /* 0 /bin 143M /boot 85M /data 0 /dev 38M /etc 4.0K /home 0 /lib 0 /lib64 16K /lostfound 4.0K /media 4.0K /mnt 31M /opt 0 /proc 260K /r…...

丰田工厂停产竟然因为磁盘...
丰田因磁盘空间不足关闭14家工厂 在如今的信息时代,无论是生活还是工作,我们都离不开计算机和网络。然而,令人惊讶的是,一家全球知名的汽车制造商——丰田,却因为磁盘空间不足的问题,被迫关闭了14家工厂。…...
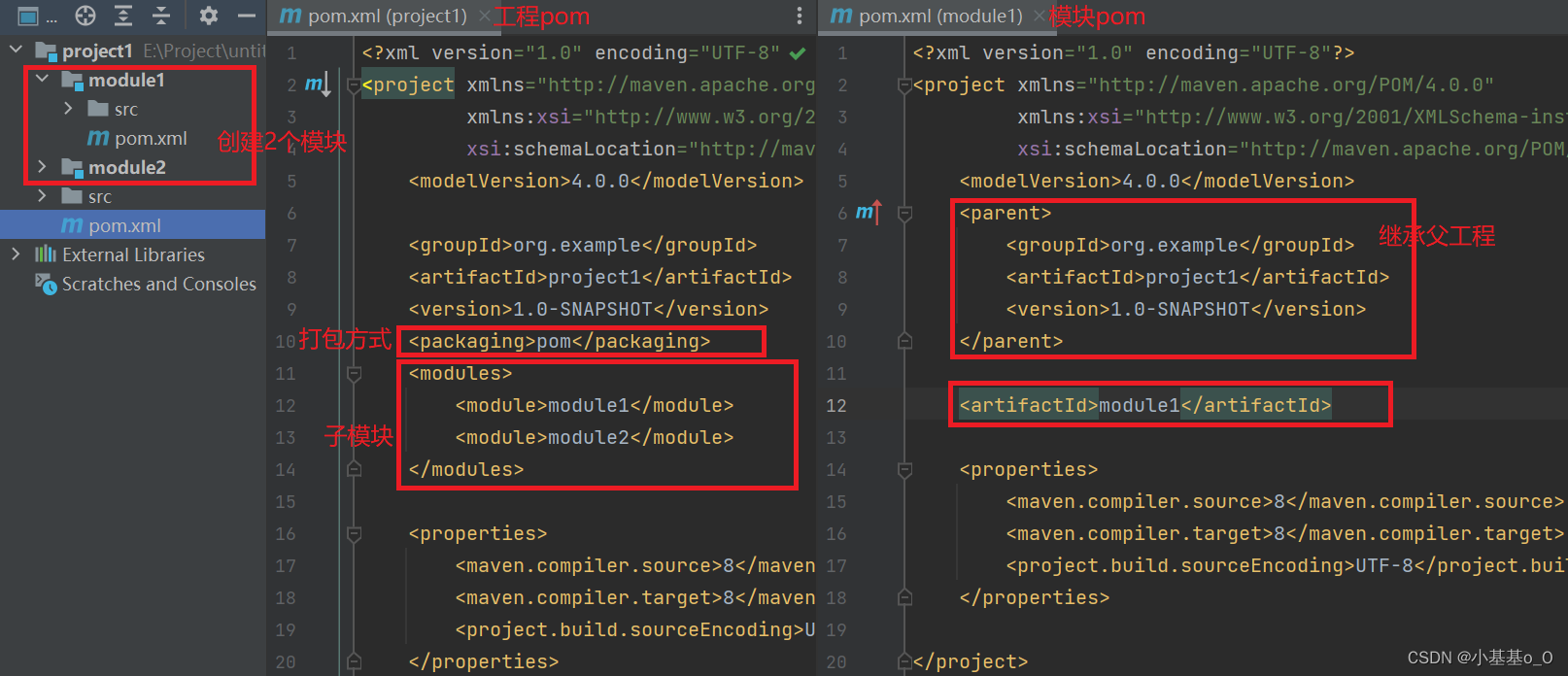
Python工程师Java之路(p)Maven聚合和继承
文章目录 依赖管理依赖传递可选依赖和排除依赖 继承与聚合 依赖管理 指当前项目运行所需的jar,一个项目可以设置多个依赖 <!-- 设置当前项目所依赖的所有jar --> <dependencies><!-- 设置具体的依赖 --><dependency><!-- 依赖所属群组…...

Java 复习笔记 - Lambda 表达式 he 经典算法题
文章目录 Lambda表达式 概述(一)基本作用(二)特点 一,初识Java中的Lambda 表达式二,函数式编程三,省略写法四,练习:使用Lambda 表达式 简化Comparator接口的匿名形式综合…...
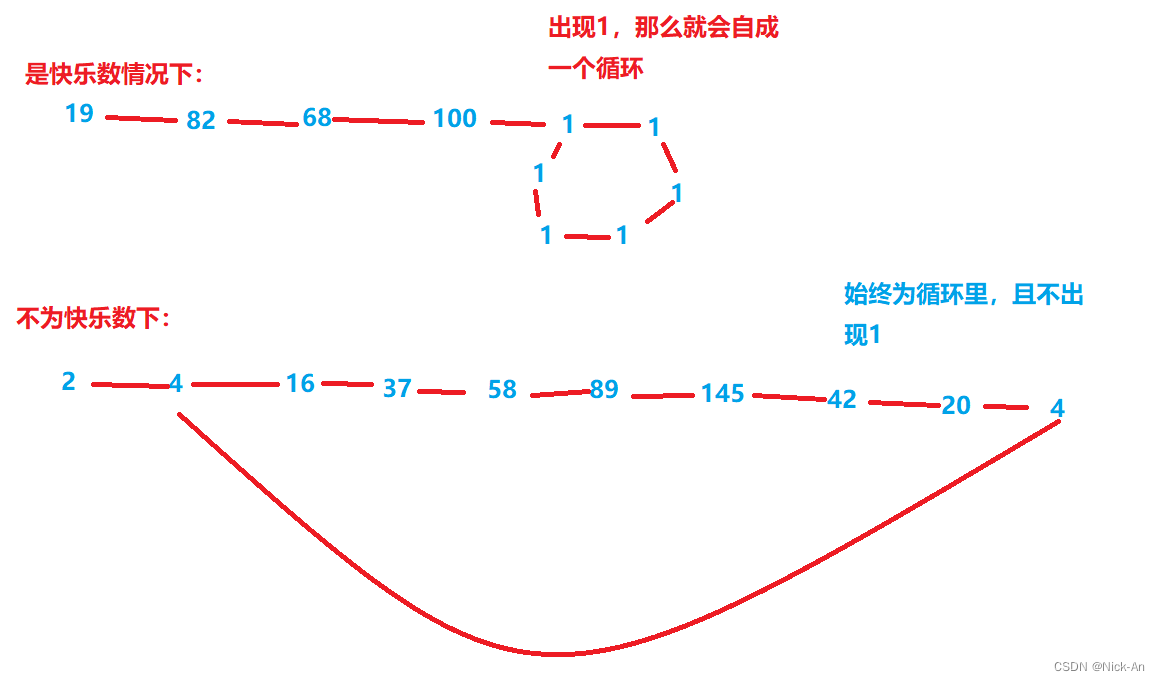
算法——快乐数
202. 快乐数 - 力扣(LeetCode) 由图可知,其实这也是一个判断循环的过程,要用到快慢指针,且相遇后,若在全为1的循环里,那么就是快乐数,若相遇后不为1,说明这不是快乐数。 …...

vue使用window.location.href 跳转失败
问题: vue项目中直接使用window.lcocation.href跳转外链,但是跳转的链接会被拼接成这样 http://localhost:8080/#/www.baidu.com 原因: 我们打开的外部链接会自动拼接我们的源地址,导致网址链接不正确,无法正常访问 …...
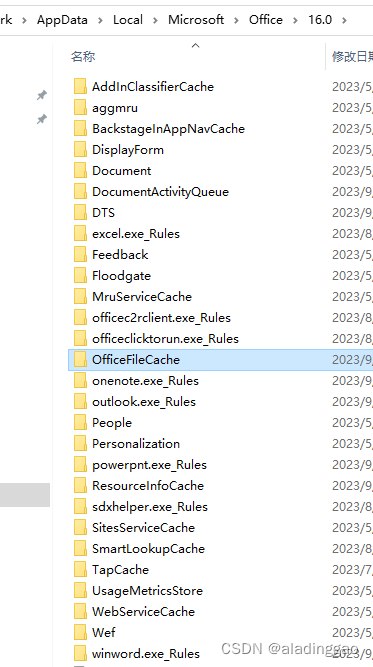
【备忘】清理Office缓存
【背景】电脑安装了M365 Apps for enterprise的客户端,遇到不常见的奇怪问题。尝试看清理缓存是否可以解决。 【清理步骤】 1. 关闭所有Office365 应用; 2. 搜索 %AppData% ,并打开该文件夹; 3. 进到 AppData > Local > M…...

MacOS环境变量source生效但重启后又失效
https://blog.csdn.net/dxk539687357/article/details/127942044 .bash_profile 和 .zshrc 都是macos系统重环境变量配置的文件,但是两者有不同之处。 .bash_profile:在执行source ~/.bash_profile,只在当前窗口生效,但关闭当前…...

Sql语句大全--插入
今天抽空整理下项目中的Sql语句 项目中用到的Sql语句大全 Insert 语句,有简有难 Insert 语句,有简有难 insert into clayor (pco,ppolnum,ptype,psn,prela,pname,pid,paddr1,paddr2,pbakcod1,pbakcod2,paccnum,pchkflag,pagtcod,pstatus, pchksts,pauth…...
吸引开发者关注)
Unity 收取“运行费”引众怒,开源免费3D游戏引擎CGE(Castle Game Engine)吸引开发者关注
特征 1. 总结2. 跨平台3. 可视化编辑器4.视口与场景,相机,导航和其他组件5. 数据格式 5.1. glTF5.2. X3D5.3. 精灵表5.4. 脊柱6. 图形效果7. 图片8. 用户界面组件 8.1. 文本和字体9. 网络10. 优化和分析11. 声音12. 物理13. 平铺集成14. 粒子15. 使用现代…...
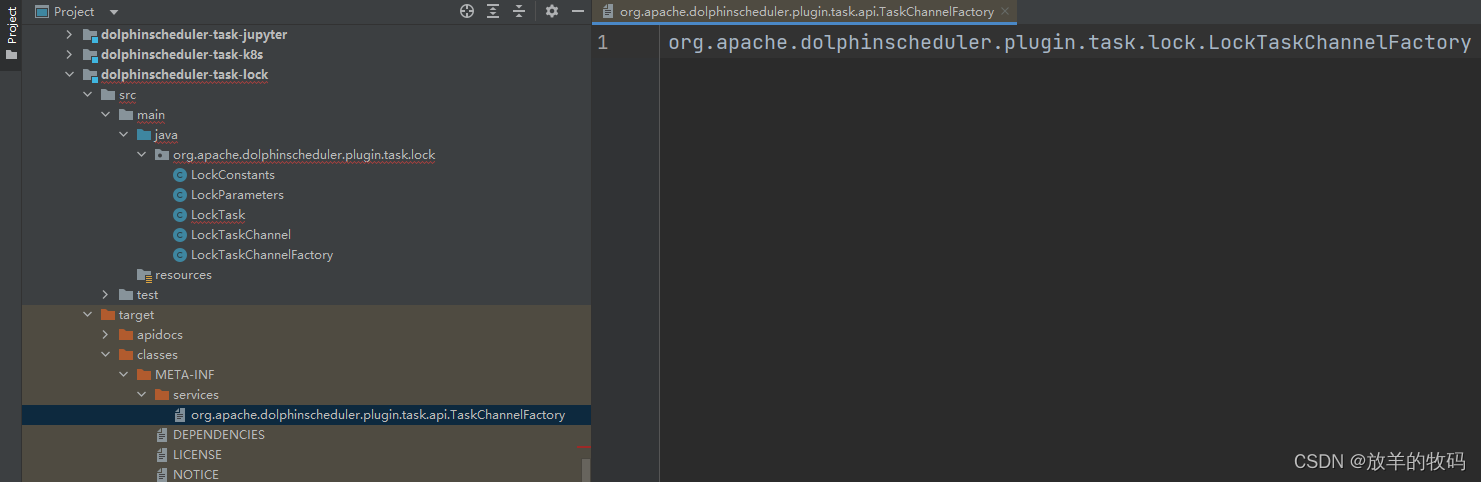
Apache DolphinScheduler - 快速扩展 TaskPlugin 从入门到放弃
目前在大数据生态中,调度系统是不可或缺的一个重要组件。Apache DolphinScheduler 作为一个顶级的 Apache 项目,其稳定性和易用性也可以说是名列前茅的。而对于一个调度系统来说,能够支持的可调度的任务类型同样是一个非常重要的因素…...
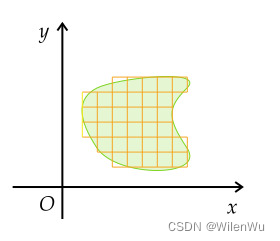
线性代数的本质(四)——行列式
文章目录 行列式二阶行列式 n n n 阶行列式行列式的性质克拉默法则行列式的几何理解 行列式 二阶行列式 行列式引自对线性方程组的求解。考虑两个方程的二元线性方程组 { a 11 x 1 a 12 x 2 b 1 a 21 x 1 a 22 x 2 b 2 \begin{cases} a_{11}x_1a_{12}x_2b_1 \\ a_{21}x_…...

适合初学者快速入门的Numpy实战全集
适合初学者快速入门的Numpy实战全集 Numpy是一个用python实现的科学计算的扩展程序库,包括: 1、一个强大的N维数组对象Array;2、比较成熟的(广播)函数库;3、用于整合C/C和Fortran代码的工具包;…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

