线性代数的本质(四)——行列式
文章目录
- 行列式
- 二阶行列式
- n n n 阶行列式
- 行列式的性质
- 克拉默法则
- 行列式的几何理解
行列式
二阶行列式
行列式引自对线性方程组的求解。考虑两个方程的二元线性方程组
{ a 11 x 1 + a 12 x 2 = b 1 a 21 x 1 + a 22 x 2 = b 2 \begin{cases} a_{11}x_1+a_{12}x_2=b_1 \\ a_{21}x_1+a_{22}x_2=b_2 \end{cases} {a11x1+a12x2=b1a21x1+a22x2=b2
可使用消元法,得
( a 11 a 22 − a 12 a 21 ) x 1 = b 1 a 22 − a 12 b 2 ( a 11 a 22 − a 12 a 21 ) x 2 = a 11 b 2 − b 1 a 21 (a_{11}a_{22}-a_{12}a_{21})x_1=b_1a_{22}-a_{12}b_2 \\ (a_{11}a_{22}-a_{12}a_{21})x_2=a_{11}b_2-b_1a_{21} (a11a22−a12a21)x1=b1a22−a12b2(a11a22−a12a21)x2=a11b2−b1a21
当 a 11 a 22 − a 12 a 21 ≠ 0 a_{11}a_{22}-a_{12}a_{21}\neq 0 a11a22−a12a21=0 时,得
x 1 = b 1 a 22 − a 12 b 2 a 11 a 22 − a 12 a 21 , x 2 = a 11 b 2 − b 1 a 21 a 11 a 22 − a 12 a 21 x_1=\frac{b_1a_{22}-a_{12}b_2}{a_{11}a_{22}-a_{12}a_{21}},\quad x_2=\frac{a_{11}b_2-b_1a_{21}}{a_{11}a_{22}-a_{12}a_{21}} x1=a11a22−a12a21b1a22−a12b2,x2=a11a22−a12a21a11b2−b1a21
从方程组解来看,分母 a 11 a 22 − a 12 a 21 a_{11}a_{22}-a_{12}a_{21} a11a22−a12a21 是系数矩阵 A = [ a 11 a 12 a 21 a 22 ] A=\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\end{bmatrix} A=[a11a21a12a22] 的元素计算得到,称这个值为矩阵 A A A 的二阶行列式(determinant),记为 det A \det A detA 或 ∣ A ∣ |A| ∣A∣ ,或记为数表形式
∣ a 11 a 12 a 21 a 22 ∣ = a 11 a 22 − a 12 a 21 \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}=a_{11}a_{22}-a_{12}a_{21} a11a21a12a22 =a11a22−a12a21
利用二阶行列式的概念,分子也可写为二阶行列式
det A 1 = ∣ b 1 a 12 b 2 a 22 ∣ = b 1 a 22 − a 12 b 2 det A 2 = ∣ a 11 b 1 a 21 b 2 ∣ = a 11 b 2 − b 1 a 21 \det A_1=\begin{vmatrix} b_1 & a_{12} \\ b_2 & a_{22}\end{vmatrix}=b_1a_{22}-a_{12}b_2 \\ \det A_2=\begin{vmatrix} a_{11} & b_1 \\ a_{21} & b_2\end{vmatrix}=a_{11}b_2-b_1a_{21} detA1= b1b2a12a22 =b1a22−a12b2detA2= a11a21b1b2 =a11b2−b1a21
从上面对比可以看出, x j x_j xj 的矩阵 A j A_j Aj 是系数矩阵 A A A的第 j j j 列用常数项代替后的矩阵。这样,方程组的解可表示为
x 1 = det A 1 det A , x 2 = det A 2 det A x_1=\frac{\det A_1}{\det A},\quad x_2=\frac{\det A_2}{\det A} x1=detAdetA1,x2=detAdetA2
n n n 阶行列式
考虑三个方程的三元线性方程组,系数矩阵为
A = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{bmatrix} A= a11a21a31a12a22a32a13a23a33
用消元法可知未知数的分母同样是系数矩阵 A A A 的元素运算得到,于是定义三阶行列式为
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 11 a 23 a 32 − a 12 a 21 a 33 − a 13 a 22 a 31 \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{vmatrix} =a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32} -a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31} a11a21a31a12a22a32a13a23a33 =a11a22a33+a12a23a31+a13a21a32−a11a23a32−a12a21a33−a13a22a31
由二阶行列式的定义,上式可变为
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 ∣ a 22 a 23 a 32 a 33 ∣ − a 12 ∣ a 21 a 23 a 31 a 33 ∣ + a 13 ∣ a 11 a 12 a 21 a 22 ∣ \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{vmatrix}= a_{11}\begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33}\end{vmatrix}- a_{12}\begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33}\end{vmatrix}+ a_{13}\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\end{vmatrix} a11a21a31a12a22a32a13a23a33 =a11 a22a32a23a33 −a12 a21a31a23a33 +a13 a11a21a12a22
进一步探索 n n n 元线性方程组,可知高阶行列式定义。为书写方便,把元素 a i j a_{ij} aij 所在的行和列划掉后,剩下的元素组成的行列式称为 a i j a_{ij} aij 的余子式(cofactor),记作 M i j M_{ij} Mij ,并称
A i j = ( − 1 ) i + j M i j A_{ij}=(-1)^{i+j}M_{ij} Aij=(−1)i+jMij
为 a i j a_{ij} aij 的代数余子式(algebraic cofactor)。
定义:方阵 A A A 的行列式用第一行元素的代数余子式定义为
det A = ∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ∣ = ∑ j = 1 n a 1 j A 1 j \det A=\begin{vmatrix} a_{11}&a_{12}&\cdots&a_{1n} \\ a_{21}&a_{22}&\cdots&a_{2n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{n1}&a_{n2}&\cdots&a_{nn} \\ \end{vmatrix}=\sum_{j=1}^na_{1j}A_{1j} detA= a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann =j=1∑na1jA1j
由定义易知,行列式可以按任意行(列)展开。
det A = ∑ j = 1 n a i j A i j , by row i det A = ∑ i = 1 n a i j A i j , by col j \det A=\sum_{j=1}^na_{ij}A_{ij}, \quad \text{by row }i \\ \det A=\sum_{i=1}^na_{ij}A_{ij}, \quad \text{by col }j detA=j=1∑naijAij,by row idetA=i=1∑naijAij,by col j
行列式的性质
性质:使用数学归纳法可知
- 行列式与其转置行列式相等: det A T = det A \det A^T=\det A detAT=detA
- 互换行列式两行(列),行列式改变符号。
∣ a b c d ∣ = − ∣ c d a b ∣ \begin{vmatrix}a&b\\c&d\end{vmatrix}=-\begin{vmatrix}c&d\\a&b\end{vmatrix} acbd =− cadb - 行列式的某一行(列)所有元素同乘以数 k k k,等于数 k k k乘以该行列式。
∣ k a b k c d ∣ = k ∣ a b c d ∣ \begin{vmatrix}ka&b\\kc&d\end{vmatrix}=k\begin{vmatrix}a&b\\c&d\end{vmatrix} kakcbd =k acbd - 若行列式的某一行(列)的为两组数之和,则可表示为两行列式之和。
∣ a 1 + a 2 b c 1 + c 2 d ∣ = ∣ a 1 b c 1 d ∣ + ∣ a 2 b c 2 d ∣ \begin{vmatrix}a_1+a_2&b\\c_1+c_2&d\end{vmatrix}=\begin{vmatrix}a_1&b\\c_1&d\end{vmatrix}+\begin{vmatrix}a_2&b\\c_2&d\end{vmatrix} a1+a2c1+c2bd = a1c1bd + a2c2bd - 把行列式的某一行(列)所有元素同乘以数 k k k 都加到另一行(列)对应的元素上去,行列式的值不变。
∣ a b c d ∣ = ∣ a + k b b c + k d d ∣ \begin{vmatrix}a&b\\c&d\end{vmatrix}=\begin{vmatrix}a+kb&b\\c+kd&d\end{vmatrix} acbd = a+kbc+kdbd - 矩阵乘积的行列式等于行列式的乘积: det ( A B ) = ( det A ) ( det B ) = det ( B A ) \det(AB)=(\det A)(\det B)=\det(BA) det(AB)=(detA)(detB)=det(BA)
推论:
- 行列式中若有两行(列)元素相同,该行列式的值为零。
- 行列式中某一行(列)的公因子可以提取到行列式符号外面。
- 行列式中若有两行(列)元素成比例,则此行列式等于零。
- det ( k A ) = k n det A \det(kA)=k^n\det A det(kA)=kndetA
由上面的性质,我们很容易得到:
- 出现零行和零列的行列式为零。
- 对角阵 A = diag ( λ 1 , λ 2 , ⋯ , λ n ) A=\text{diag}(\lambda_1,\lambda_2,\cdots,\lambda_n) A=diag(λ1,λ2,⋯,λn) 的行列式 det A = λ 1 λ 2 ⋯ λ n \det A=\lambda_1\lambda_2\cdots\lambda_n detA=λ1λ2⋯λn 。
- 如果 A A A 是三角阵,行列式为主对角线元素的乘积。
对于高阶行列式,一般利用行列式的性质,初等变换化为三角行列式求解。
示例:可用数学归纳法证明范德蒙行列式(Vandermonde determinant):
∣ 1 1 ⋯ 1 a 1 a 2 ⋯ a n a 1 2 a 2 2 ⋯ a n 2 ⋮ ⋮ ⋮ ⋮ a 1 n − 1 a 2 n − 1 ⋯ a n n − 1 ∣ = ∏ 1 ⩽ i < j ⩽ n ( a j − a i ) \begin{vmatrix} 1 & 1& \cdots &1 \\ a_1 &a_2&\cdots &a_n \\ a_1^2 &a_2^2&\cdots &a_n^2 \\ \vdots &\vdots&\vdots &\vdots \\ a_1^{n-1} &a_2^{n-1}&\cdots &a_n^{n-1} \end{vmatrix}=\prod_{1⩽ i<j⩽n}(a_j-a_i) 1a1a12⋮a1n−11a2a22⋮a2n−1⋯⋯⋯⋮⋯1anan2⋮ann−1 =1⩽i<j⩽n∏(aj−ai)
行列式函数:若 A A A 为 n n n阶矩 阵,可以将 det A \det A detA 看作 A A A 中 n n n 个列向量的函数。若 A A A 中除了一列之外都是固定的向量,则 det A \det A detA 是线性函数。
假设第 j j j 列是变量,定义映射 x ↦ T ( x ) \mathbf x\mapsto T(\mathbf x) x↦T(x) 为
T ( x ) = det A = det [ a 1 ⋯ x ⋯ a n ] T(\mathbf x)=\det A=\det\begin{bmatrix}\mathbf a_1\cdots\mathbf x\cdots\mathbf a_n\end{bmatrix} T(x)=detA=det[a1⋯x⋯an]
则有
T ( c x ) = c T ( x ) T ( u + v ) = T ( u ) + T ( v ) T(c\mathbf x)=cT(\mathbf x) \\ T(\mathbf u+\mathbf v)=T(\mathbf u)+T(\mathbf v) T(cx)=cT(x)T(u+v)=T(u)+T(v)
克拉默法则
这里只讨论方程个数和未知数相等的 n n n元线性方程组
A x = b A\mathbf x=\mathbf b Ax=b
若 det A ≠ 0 \det A\neq0 detA=0,那么它有唯一解
x j = det A j ( b ) det A , ( j = 1 , 2 , ⋯ , n ) x_j=\frac{\det A_j(\mathbf b)}{\det A},\quad(j=1,2,\cdots,n) xj=detAdetAj(b),(j=1,2,⋯,n)
约定 A j ( b ) A_j(\mathbf b) Aj(b) 表示用向量 b \mathbf b b 替换矩阵 A A A的第 j j j列。
证:用 a 1 , a 2 , ⋯ , a n \mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n a1,a2,⋯,an 表示矩阵 A A A 的各列, e 1 , e 2 , ⋯ , e n \mathbf e_1,\mathbf e_2,\cdots,\mathbf e_n e1,e2,⋯,en 表示单位阵 I n I_n In 的各列。由分块矩阵乘法
A I j ( x ) = A [ e 1 ⋯ x ⋯ e n ] = [ A e 1 ⋯ A x ⋯ A e n ] = [ a 1 ⋯ b ⋯ a n ] = A j ( b ) \begin{aligned} AI_j(\mathbf x)&=A\begin{bmatrix}\mathbf e_1&\cdots&\mathbf x&\cdots&\mathbf e_n\end{bmatrix} \\ &=\begin{bmatrix}A\mathbf e_1&\cdots& A\mathbf x&\cdots& A\mathbf e_n\end{bmatrix} \\ &=\begin{bmatrix}\mathbf a_1&\cdots&\mathbf b&\cdots&\mathbf a_n\end{bmatrix} \\ &=A_j(\mathbf b) \end{aligned} AIj(x)=A[e1⋯x⋯en]=[Ae1⋯Ax⋯Aen]=[a1⋯b⋯an]=Aj(b)
由行列式的乘法性质
det A det I j ( x ) = det A j ( b ) \det A\det I_j(\mathbf x)=\det A_j(\mathbf b) detAdetIj(x)=detAj(b)
左边第二个行列式可沿第 j j j 列余子式展开求得 det I j ( x ) = x j \det I_j(\mathbf x)=x_j detIj(x)=xj。从而
x j det A = det A j ( b ) x_j\det A=\det A_j(\mathbf b) xjdetA=detAj(b)
若 det A ≠ 0 \det A\neq0 detA=0,则上式得证。
行列式的几何理解
Grant:行列式告诉你一个线性变换对区域的缩放比例。
我们已经知道,线性变换保持网格线平行且等距。为了方便,我们只考虑在平面直角坐标系内,单位基向量 i , j \mathbf i,\mathbf j i,j 所围成的单位正方形区域的线性变换。
根据向量加法的平行四边形法则和线性变换基本性质知,变换后的区域为矩阵 A = [ a b c d ] A=\begin{bmatrix}a & b\\c & d\end{bmatrix} A=[acbd] 的列向量 [ a c ] \begin{bmatrix}a\\c\end{bmatrix} [ac] 和 [ b d ] \begin{bmatrix}b\\d\end{bmatrix} [bd] 为邻边的平行四边形区域。
结论:二阶行列式的值表示由 A A A 的列确定的有向平行四边形的面积。
(1) 若 A A A 为对角阵,显然行列式 det [ a b 0 d ] \det\begin{bmatrix}a & b\\0 & d\end{bmatrix} det[a0bd] 表示底为 a a a,高为 d d d 的平行四边形面积

(2) 更一般的情况 A = [ a b c d ] A=\begin{bmatrix}a & b\\c & d\end{bmatrix} A=[acbd] ,可以看出,行列式的值与面积有着紧密的联系。

(3) 矩阵 [ a 2 a a 1 ] \begin{bmatrix}a^2 & a\\a & 1\end{bmatrix} [a2aa1] 表示将单位正方形压缩成线段,面积自然为0,行列式的值为0

单位正方形区域缩放的比例,其实可以代表任意给定区域缩放的比例。这是因为,线性变换保持网格线平行且等距。对于空间中任意区域的面积,借助微积分的思想,我们可以采用足够的小方格来逼近区域的面积,对所有小方格等比例缩放,则整个区域也以同样的比例缩放。
volume T ( Ω ) = ( det T ) ( volume Ω ) \text{volume }T(\Omega) = (\det T)(\text{volume }\Omega) volume T(Ω)=(detT)(volume Ω)
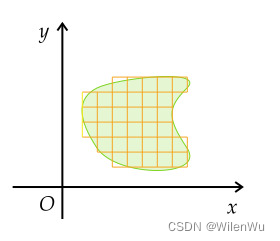
通过行列式的几何意义,我们就建立了线性变换、矩阵、行列式之间的关系。不难得出
- 复合线性变换缩放的比例相当于每次变换缩放比例的乘积,即
det A B = det A det B \det AB=\det A\det B detAB=detAdetB - 行列式的值为零,表示将空间压缩到更低的维度,矩阵的列向量线性相关
相关文章:

线性代数的本质(四)——行列式
文章目录 行列式二阶行列式 n n n 阶行列式行列式的性质克拉默法则行列式的几何理解 行列式 二阶行列式 行列式引自对线性方程组的求解。考虑两个方程的二元线性方程组 { a 11 x 1 a 12 x 2 b 1 a 21 x 1 a 22 x 2 b 2 \begin{cases} a_{11}x_1a_{12}x_2b_1 \\ a_{21}x_…...

适合初学者快速入门的Numpy实战全集
适合初学者快速入门的Numpy实战全集 Numpy是一个用python实现的科学计算的扩展程序库,包括: 1、一个强大的N维数组对象Array;2、比较成熟的(广播)函数库;3、用于整合C/C和Fortran代码的工具包;…...

rabbitmq 面试题
1.交换机类型 RabbitMQ是一个开源的消息队列系统,它支持多种交换机类型,用于在消息的生产者和消费者之间路由和分发消息 Direct Exchange(直接交换机):Direct交换机是最简单的交换机类型之一。它将消息按照消息的Rout…...
比较Visual Studio Code中的文件
目录 一、比较两个文件 1.1VS code中的文件大致分为两类: 1.2如何比较VS code中的两个文件? 二、并排差异模式:VS code中的一种差异模式 三、内联差异模式:VS code中的另一种差异模式 四、VS code忽略在行首或者行尾添加或删除…...

誉天在线项目-UML状态图+泳道图
什么是UML UML(Unified Modeling Language)是一种用于软件系统建模的标准化语言。它提供了一组图形符号和规范,用于描述和设计软件系统的结构、行为和交互。 UML图形符号包括类图、用例图、时序图、活动图、组件图、部署图等,每…...

【linux基础(六)】Linux中的开发工具(中)--gcc/g++
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:Linux从入门到开通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学更多操作系统知识 🔝🔝 Linux中的开发工具 1. 前言2.…...
u盘上面 安装 ubuntu 系统
u盘上面 安装 ubuntu 系统 下载 一个 Ubuntu 22.04.3 LTS 桌面版 https://ubuntu.com/download/desktop 找到一个U盘 参考文章: 把 Ubuntu 装到U盘里随身携带,并同时支持 BIOS 和 UEFI 启动 https://www.luogu.com.cn/blog/GGAutomaton/portable-ubu…...
【推荐】SpringMVC与JSON数据返回及异常处理机制的使用
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《【推荐】Spring与Mybatis集成整合》 ⛺️ 生活的理想,为了不断更新自己 ! 1.JSON 在SpringMVC中,JSON数据返回通常是通过使用ResponseBody注解将Java对象转换为JSO…...

SpringBoot新增拦截器详解
目录 一、拦截器使用 二、SpringMvc拦截器接口 三、SpringBoot集成拦截器 拦截器(Interceptor)通常是指在软件开发中用于处理请求和响应的中间件组件。拦截器的主要目的是在请求进入某个处理流程或在响应返回给客户端之前执行一些额外的操作或逻辑。 …...

Golang开发--select
在Go语言中,select语句用于在多个通道操作中进行选择。select语句使得程序可以同时等待多个通道的操作,并在其中任意一个通道就绪时执行相应的操作。以下是select语句的详细描述: select { case <-ch1:// 当ch1通道可读时执行的操作 case…...
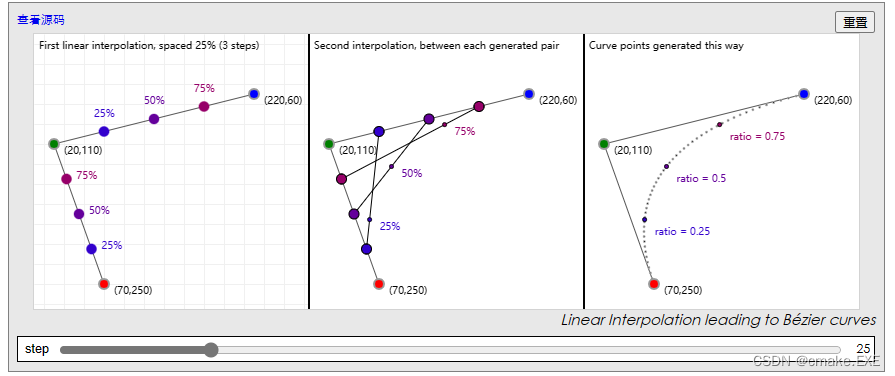
贝塞尔曲线的一些资料收集
一本免费的在线书籍,供你在非常需要了解如何处理贝塞尔相关的事情。 https://pomax.github.io/bezierinfo/zh-CN/index.html An algorithm to find bounding box of closed bezier curves? - Stack Overflow https://stackoverflow.com/questions/2587751/an-algo…...

计算机网络原理 运输层
一,运输层协议概述 1,进程之间的通信 从通信和信息处理的角度看,运输层向它上面的应用层提供通信服务,它属于面向通信部分的最高层,同时也是用户功能中的最底层。当网络边缘部分的两台主机使用网络核心部分的功能进行…...

【JavaEE】多线程案例-阻塞队列
1. 前言 阻塞队列(BlockingQueue)是一个支持两个附加操作的队列。这两个附加的操作是: 在队列为空时,获取元素的线程会等待队列变为非空当队列满时,存储元素的线程会等待队列可用 阻塞队列常用于生产者和消费者的场…...
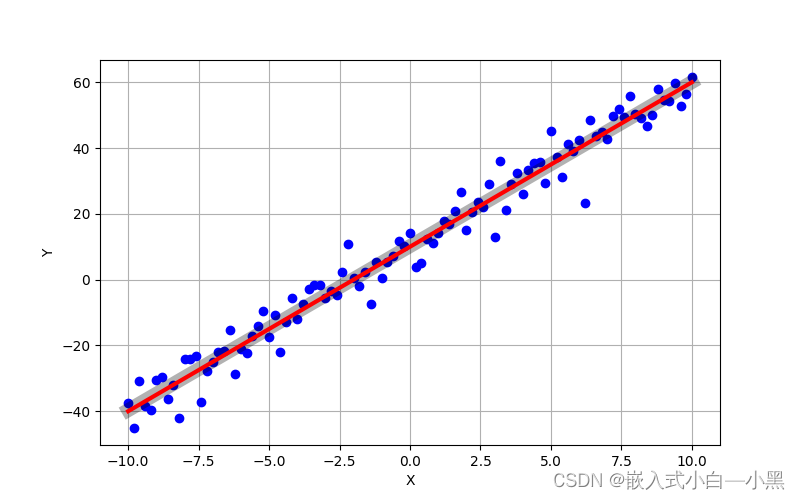
【物联网】简要介绍最小二乘法—C语言实现
最小二乘法是一种常用的数学方法,用于拟合数据和寻找最佳拟合曲线。它的目标是找到一个函数,使其在数据点上的误差平方和最小化。 文章目录 基本原理最小二乘法的求解应用举例使用C语言实现最小二乘法总结 基本原理 假设我们有一组数据点 ( x 1 , y 1 …...

慢查询SQL如何优化
一.什么是慢SQL? 慢SQL指的是Mysql中执行比较慢的SQL,排查慢SQL最常用的方法是通过慢查询日志来查找慢SQL。Mysql的慢查询日志是Mysql提供的一种日志记录,它用来记录Mysql中响应时间超过long_query_time值的sql,long_query_time的默认时间为10s. 二.查看慢SQL是否…...

UART 通信-使用VIO进行板级验证
串口系列知识分享: (1)串口通信实现-串口发送 (2)串口通信发送多字节数据 (3)串口通信实现-串口接收 (4)UART 通信-使用VIO进行板级验证 (5)串口接收-控制LED闪烁 (6)使用串口发送实现ACX720开发板时钟显示 (7)串口发送+RAM+VGA传图 文章目录 前言一、uart串口协…...

linux 查看可支持的shell
查看可支持的shell linux中支持多种shell类型,所以在shell文件的第一行需要指定所使用的shell #!/bin/bash 指定该脚本使用的是/bin/bash,这样的机制使得我们可以轻松地引用任何的解释器 查看该linux系统支持的shell cat /etc/shells/bin/sh/bin/bash/us…...

微服务简介
微服务简介 微服务架构是一种软件架构模式,它将一个大型应用程序拆分为一组小型、独立的服务,每个服务都有自己的业务逻辑和数据存储。这些服务可以独立开发、部署和扩展,通常使用HTTP或其他轻量级通信协议进行通信。 以下是微服务架构的一…...
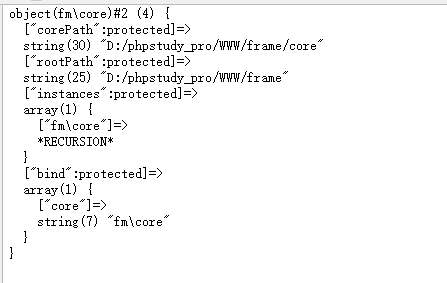
PHP自己的框架2.0设置常量并绑定容器(重构篇三)
目录 1、设置常量并绑定容器 2、容器增加设置当前容器的实例和绑定一个类实例当容器 3、将常量绑定到容器中 4、运行效果 1、设置常量并绑定容器 2、容器增加设置当前容器的实例和绑定一个类实例当容器 //设置当前容器的实例public static function setInstance($instance){…...

重建大师提交空三后引擎状态是等待,怎么开启?
答:图片中这是在自由网空三阶段,整个AT都是等待中,可以修改任务目录和监控目录看一下,先设置引擎,再提交空三。...
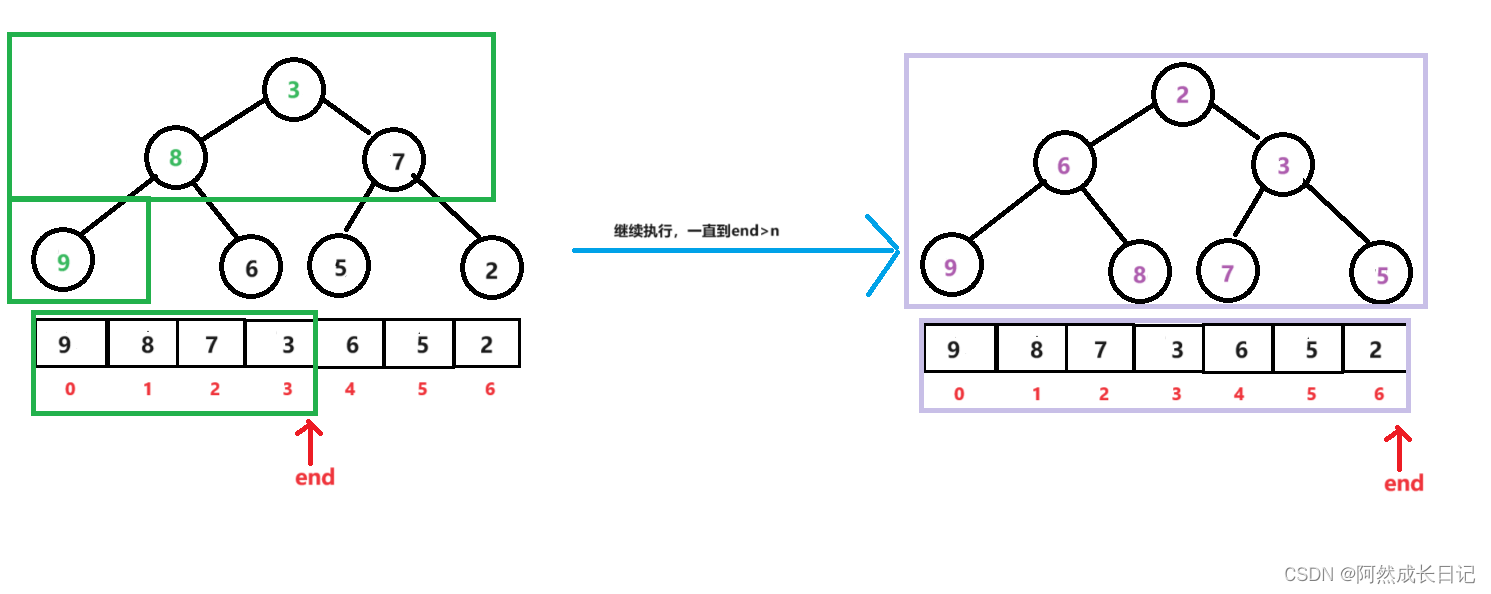
【数据结构】堆的向上调整和向下调整以及相关方法
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃 文章目录 一、堆的概念二、堆的性质…...

【蓝桥杯选拔赛真题60】Scratch旋转风车 少儿编程scratch图形化编程 蓝桥杯选拔赛真题解析
目录 scratch旋转风车 一、题目要求 编程实现 二、案例分析 1、角色分析...

JavaSE、JavaEE与Spring的概念和异同点剖析以及规范13 个分析
JavaSE、JavaEE与Spring的概念和异同点剖析以及规范13 个分析 目录概述需求: 设计思路实现思路分析1.什么是JavaSE2.是JavaEE3.什么是Spring 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy&…...
微信小程序的图书馆图书借阅 座位预约系统 读者端设计与实现
该系统基于B/S即所谓浏览器/服务器模式,应用springboot框架,选择MySQL作为后台数据库。系统主要包括系统图书信息、图书借阅、图书归还、自习室信息、自习室预约等功能模块。 关键词 微信小程序的图书馆读者端;微信小程序;java语…...
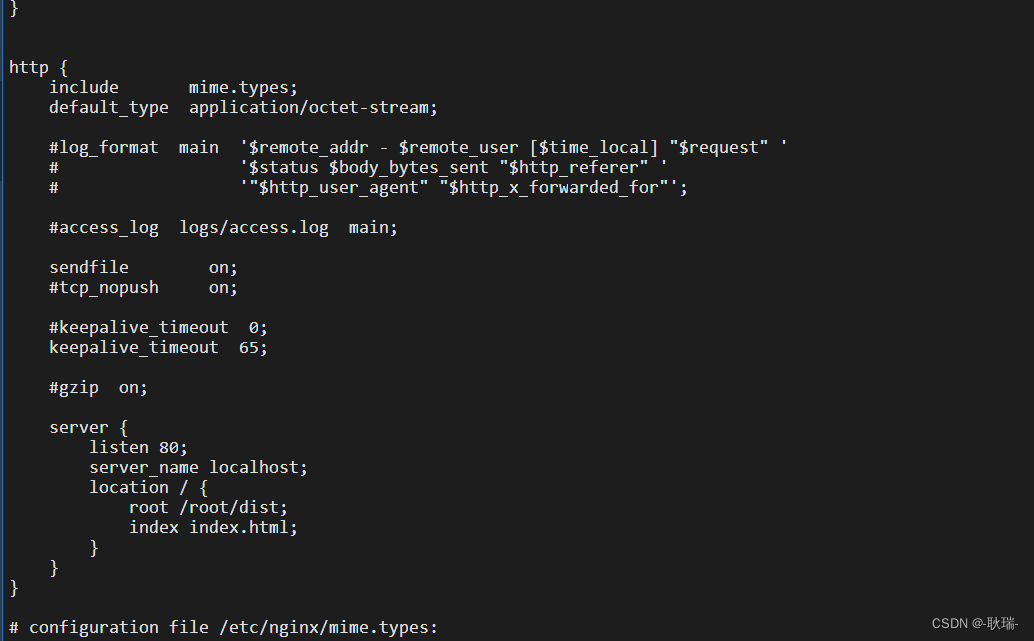
在阿里云 linux 服务器上查看当前服务器的Nginx配置信息
我们可以通过命令 sudo nginx -t查看到nginx.conf的路径 可以通过 sudo nginx -T查看 nginx 详细配置信息,包括加载的配置文件和配置块的内容 其中也会包括配置文件的内容...

专业招投标书翻译怎样做比较好
在全球经济贸易一体化不断深入的时代,招投标作为国际通用的新型贸易方式,受到了大量中外企业的青睐。根据国际惯例,与招标采购活动有关的一切文件资料,均须使用英文编制。即使允许使用非英文语言编制,也必须随附一份英…...
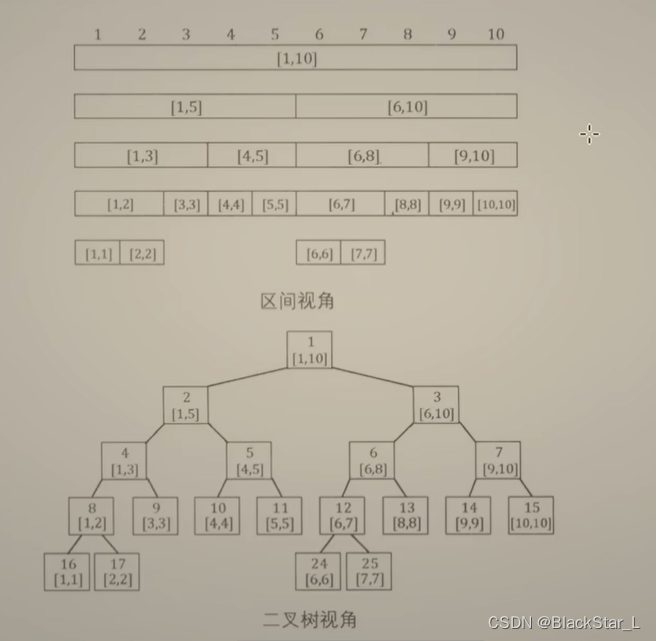
算法总结10 线段树
算法总结10 线段树 线段树2569. 更新数组后处理求和查询 线段树 有一个数组,我们要: 更新数组的值(例如:都加上一个数,把子数组内的元素取反)查询一个子数组的值(例如:求和&#x…...

518抽奖软件,支持按人像照片抽奖
518抽奖软件简介 518抽奖软件,518我要发,超好用的年会抽奖软件,简约设计风格。 包含文字号码抽奖、照片抽奖两种模式,支持姓名抽奖、号码抽奖、数字抽奖、照片抽奖。(www.518cj.net) 照片抽奖模式 圆角边框 照片抽奖模式下&am…...
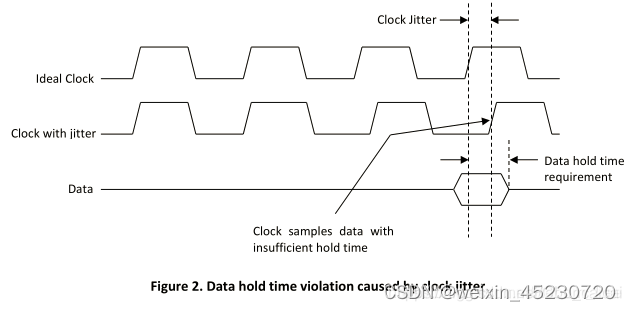
数字IC笔试面试题之--时钟偏斜(skew)与抖动(jitter)
1 时钟偏斜(clock skew) 时钟偏斜(偏移)是因为布线长度和负载不同,导致同一时钟上升沿到不同触发器的时间不同。这一时间差,即为时钟偏移。 时钟偏斜可能导致时序违例(本文直接粘贴了参考博客…...

免费api接口:物流api,企业工商查询api,游戏api。。。
免费api接口,物流api,企业工商查询api,游戏api。。。都有。 Facebook Games Services - Facebook Games Services 为游戏开发者提供了各种服务, 包括(但不限于) 成就 API, 分数 API, 应用通知, 请求, 游戏养成和 Facebook SDK for Unity.Google Play Games Service…...
