DM@命题公式@主范式的性质和应用@数理逻辑解决数字电路全加器问题
文章目录
- abstract
- 主合取范式与主析取范式间的关系👺
- 主范式存在及唯一性定理
- 例
- 主范式的性质👺
- 求公式的成真与成假赋值
- 主析取范式直接得到主合取范式
- 判断公式的类型
- n n n元命题公式的主析取范式(主合取范式)的个数
- 判断两个命题公式是否等值
- 给出一个满足给定真值表的命题公式
- 半加器
- 全加器
- 半加器和全加器的联系
- 主范式合并化简
- 卡诺图法
- 公式法
- 最简范式
abstract
- 命题公式@
- 主范式的性质和应用
- @数理逻辑解决数字电路全加器问题
主合取范式与主析取范式间的关系👺
- 同一个 n n n元命题公式 A A A的主合取范式 A 1 A_1 A1与主析取范式 A 2 A_2 A2间的关系:
- 构造整数集合 S = { 0 , ⋯ , 2 n − 1 } S=\{0,\cdots,2^{n}-1\} S={0,⋯,2n−1},以及主析取式的所有最小项编号构成的集合 m = ( i 1 , ⋯ , i t ) m=(i_1,\cdots,i_t) m=(i1,⋯,it),其中 t t t是主取析范式包含的极小项数目
- 作整数下标集合 M = S − m M=S-m M=S−m= { j 1 , ⋯ , j s } \{j_1,\cdots,j_{s}\} {j1,⋯,js},其中 s = 2 n − t s=2^{n}-t s=2n−t,则主合取范式就是 M j 1 ∧ M j 2 ⋯ M j s M_{j_1}\wedge{M_{j_2}}\cdots{M_{j_{s}}} Mj1∧Mj2⋯Mjs
- 总之, A 1 , A 2 A_1,A_2 A1,A2的下标相对于 S S S集合是互补的
- 证明:参考主范式的性质一节(根据主析取范式直接得到主合取范式)
主范式存在及唯一性定理
- 任何命题公式都存在与之等值的主析取范式和主合取范式
- 存在性
- 按照命题公式主范式化一节给出的方法可以将所有析取范式(合取范式)主规范化
- 又因为任意命题都可以规范化为析取范式和合取范式
- 所以存在性成立
- 唯一性(以析取范式为例,用反证法证明)
- 即证明任意公式的主析取范式都式一致的,又即任意两个析取范式包含的最小项一致(最小项编号序列一致)
- 不妨设 B , C B,C B,C是 A A A的任意两个不同的主析取范式,则 B ⇔ C B\Leftrightarrow{C} B⇔C
- 设 m i m_i mi只出现在 B B B中而不出现在 C C C中;于是 i i i对应的二进制串 x 1 ⋯ x n x_1\cdots{x_n} x1⋯xn是 B B B的成真赋值,但不是 C C C的成真赋值,与 B ⇔ C B\Leftrightarrow{C} B⇔C矛盾
- 所以 B , C B,C B,C的包含的最小项相同,即 B , C B,C B,C是同一个主析取范式
- 所以唯一性成立
- 主合取发生范式的证明类似
例
- ( p → q ) → r (p\to{q})\to{r} (p→q)→r ⇔ \Leftrightarrow ⇔ ( p ∧ ¬ q ∧ ¬ r ) (p\wedge{\neg{q}}\wedge\neg{r}) (p∧¬q∧¬r) ∨ \vee ∨ ( ¬ p ∧ r ) {(\neg{p}\wedge{r}}) (¬p∧r) ∨ \vee ∨ ( q ∧ r ) {(q\wedge{r})} (q∧r)
- ( p ∧ ¬ q ∧ ¬ r ) (p\wedge{\neg{q}}\wedge\neg{r}) (p∧¬q∧¬r)是最小项,其成真赋值二进制串为100,记为 m ( 100 ) m_{(100)} m(100)十进制下表示为 m 4 m_4 m4
- ( ¬ p ∧ r ) {(\neg{p}\wedge{r}}) (¬p∧r) ⇔ \Leftrightarrow ⇔ m 1 ∨ m 3 m_1\vee{m_3} m1∨m3
- ( q ∧ r ) {(q\wedge{r})} (q∧r) ⇔ \Leftrightarrow ⇔ m 3 ∨ m 7 m_3\vee{m_7} m3∨m7
- 所以主析取式为 ( p → q ) → r (p\to{q})\to{r} (p→q)→r ⇔ \Leftrightarrow ⇔ m 1 ∨ m 3 ∨ m 4 ∨ m 7 m_1\vee{m_3}\vee{m_4}\vee{m_7} m1∨m3∨m4∨m7
- p ∨ q p\vee{q} p∨q
- 容易看出它本身就是一个二元极大项,且是主合取范式,标号为 0 0 0,即 M 0 M_{0} M0
- 根据两种主范式关系,其主析取范式为 m 1 ∨ m 2 ∨ m 3 m_1\vee m_2\vee m_3 m1∨m2∨m3
- 如果要用基础方法计算主析取范式,过程如下
- p ∨ q p\vee{q} p∨q ⇔ \Leftrightarrow ⇔ ( p ∧ ( q ∨ ¬ q ) ) ∨ ( ( p ∨ ¬ p ) ∧ q ) (p\wedge{(q\vee{\neg{q}})})\vee{((p\vee{\neg{p}})\wedge{q})} (p∧(q∨¬q))∨((p∨¬p)∧q)
- ⇔ \Leftrightarrow ⇔ ( ( p ∧ q ) ∨ ( p ∧ ¬ q ) ) ((p\wedge{q})\vee{(p\wedge{\neg{q})}}) ((p∧q)∨(p∧¬q)) ∨ \vee ∨ ( ( p ∧ q ) ∨ ( ¬ p ∧ q ) ) ((p\wedge{q})\vee{(\neg{p}\wedge{q})}) ((p∧q)∨(¬p∧q))
- ⇔ \Leftrightarrow ⇔ ( p ∧ q ) ∨ ( p ∧ ¬ q ) (p\wedge{q})\vee{(p\wedge{\neg{q})}} (p∧q)∨(p∧¬q) ∨ \vee ∨ ( ¬ p ∧ q ) {(\neg{p}\wedge{q})} (¬p∧q)
- ⇔ \Leftrightarrow ⇔ m 3 ∨ m 2 ∨ m 1 m_3\vee{m_2}\vee{m_1} m3∨m2∨m1
- ⇔ \Leftrightarrow ⇔ m 1 ∨ m 2 ∨ m 3 m_1\vee{m_2}\vee{m_3} m1∨m2∨m3
- p ∨ q p\vee{q} p∨q ⇔ \Leftrightarrow ⇔ ( p ∧ ( q ∨ ¬ q ) ) ∨ ( ( p ∨ ¬ p ) ∧ q ) (p\wedge{(q\vee{\neg{q}})})\vee{((p\vee{\neg{p}})\wedge{q})} (p∧(q∨¬q))∨((p∨¬p)∧q)
主范式的性质👺
求公式的成真与成假赋值
-
首先,我们知道给定一个 n n n元命题公式 A A A,其真值表有 2 n 2^{n} 2n个条目(所有的 n n n元命题公式可以产生 2 2 n 2^{2^{n}} 22n个条目)
-
集合定义: S = { 1 , ⋯ , 2 n − 1 } S=\{1,\cdots,2^{n}-1\} S={1,⋯,2n−1}
-
若公式 A A A中含有 n n n个命题变项,则 A A A的主析取范式含有 s ( 0 ⩽ s ⩽ 2 n ) s(0\leqslant{s}\leqslant{2^{n}}) s(0⩽s⩽2n)个极小项,且 A A A恰好有 s s s个成真赋值,这些成真赋值恰好是所含极小项下标的二进制串表示,其余 2 n − s 2^{n}-s 2n−s个赋值都是成假赋值
- 设 A A A ⇔ \Leftrightarrow ⇔ m i 1 ∨ ⋯ ∨ m i s m_{i_1}\vee\cdots\vee m_{i_s} mi1∨⋯∨mis, m i j = ( q 1 ) ∧ ⋯ ∧ ( q n ) m_{ij}=(q_1)\wedge\cdots\wedge{(q_n)} mij=(q1)∧⋯∧(qn),其中 j = 1 , ⋯ , s j=1,\cdots,s j=1,⋯,s, ( q r ) , r = 1 , ⋯ , n (q_{r}),r=1,\cdots,n (qr),r=1,⋯,n表示 q r q_r qr或 ¬ q r \neg q_r ¬qr
- A A A为真当且仅当 m i j m_{ij} mij中至少有一个真值为真,显然 i 1 , ⋯ , i s i_1,\cdots,i_s i1,⋯,is分别使得 m i 1 , ⋯ , m i s m_{i_1},\cdots,m_{i_s} mi1,⋯,mis为真,也就能使 A A A为真
- 除此 s s s个成真赋值外,所有赋值 j 1 , ⋯ , j t j_1,\cdots,j_{t} j1,⋯,jt( t = 2 n − s t=2^{n}-s t=2n−s个)都不能使 m i 1 , ⋯ , m i s m_{i_1},\cdots,m_{i_s} mi1,⋯,mis中地任何一个成真,相应地 A A A成假
- 上述结论表明,我们可以从给定的主析取范式中直接根据各个极小项的下标得出所有的成真赋值( i 1 , ⋯ , i s i_1,\cdots,i_s i1,⋯,is);然后用集合 S S S减去成真赋值下标构成的集合(也就是主析取式中未出现的下标集合),就是所有成假赋值的集合 ( j 1 , ⋯ , j t ) , t = 2 n − s (j_1,\cdots,j_t),t=2^{n}-s (j1,⋯,jt),t=2n−s
主析取范式直接得到主合取范式
- 类似的分析主合取范式
- 对于主合取范式, A A A ⇔ \Leftrightarrow ⇔ M j 1 ∧ ⋯ ∧ M j w M_{j_1}\wedge\cdots\wedge M_{j_w} Mj1∧⋯∧Mjw, M j k = ( q 1 ) ∨ ⋯ ∨ ( q n ) M_{jk}=(q_1)\vee\cdots\vee{(q_n)} Mjk=(q1)∨⋯∨(qn),其中 ( q r ) , r = 1 , ⋯ , n (q_{r}),r=1,\cdots,n (qr),r=1,⋯,n表示 q r q_r qr或 ¬ q r \neg q_r ¬qr
- 赋值 j 1 , ⋯ , j w j_1,\cdots,j_w j1,⋯,jw分别使得 M j 1 , ⋯ , M j w M_{j_1},\cdots,M_{jw} Mj1,⋯,Mjw成假,因而它们的合取公式成假,即使得 A A A成假
- 其余赋值使得 M j 1 , ⋯ , M j w M_{j_1},\cdots,M_{jw} Mj1,⋯,Mjw都成真,即使 A A A成真
- 因此,若已知 A A A的主析取范式有 s s s个极小项 ( 0 < s < 2 n ) (0<s<2^{n}) (0<s<2n),即 A A A有 s s s个成真赋值,
- 则 A A A有 w = 2 n − s w=2^{n}-s w=2n−s个成假赋值, A A A的主合取范式有 w = 2 n − s w=2^{n}-s w=2n−s项的极大项
- 设 w w w个极大项的下标分别是 j 1 , ⋯ , j w j_1,\cdots,j_w j1,⋯,jw,它们和极小项下标 i 1 , ⋯ , i s i_1,\cdots,i_s i1,⋯,is恰好能一一对应 S S S中的元素
- 事实上, m j 1 ⋯ m j w m_{j_1}\cdots{m_{j_w}} mj1⋯mjw是 ¬ A \neg{A} ¬A的极小项: ¬ A = m j 1 ∨ ⋯ ∨ m j w \neg{A}=m_{j_1}\vee\cdots\vee{m_{jw}} ¬A=mj1∨⋯∨mjw
- A A A ⇔ \Leftrightarrow ⇔ ¬ ¬ A \neg{\neg{A}} ¬¬A ⇔ \Leftrightarrow ⇔ ¬ ( m j 1 ∨ ⋯ ∨ m j w ) \neg{(m_{j_1}\vee\cdots\vee{m_{jw}})} ¬(mj1∨⋯∨mjw) ⇔ \Leftrightarrow ⇔ ¬ m j 1 ∧ ⋯ ∧ ¬ m j w \neg m_{j_1}\wedge\cdots\wedge\neg{m_{jw}} ¬mj1∧⋯∧¬mjw ⇔ \Leftrightarrow ⇔ M j 1 ∧ ⋯ ∧ M j w M_{j_1}\wedge{\cdots}\wedge{M_{jw}} Mj1∧⋯∧Mjw
- 上述分析解释了主合取范式与主析取范式间的关系,并且说明了为什么主析取范式和主合取范式共同反映(容易还原)真值表所能表达的全部信息
判断公式的类型
- 主范式能判断公式类型,这也是主范式能体现真值表的表现
- 设 A A A中含有 n n n个命题变项,则
- 从极小项的角度
- A A A为重言式当且仅当 A A A的主析取范式包含 2 n 2^{n} 2n个极小项( A A A有 2 n 2^{n} 2n个成真赋值)
- A A A为矛盾是当且仅当 A A A的主析取范式不含任何极小项(主合取范式包含 2 n 2^{n} 2n个极大项, A A A有 2 n 2^{n} 2n个成假赋值);此时 A A A的主析取范式为0(表示矛盾式)
- A A A为可满足式当且仅当 A A A的主析取范式包含至少一个极小项
- 从极大项的角度
- A A A为重言式当且仅当 A A A的主合取范式不含极大项(规定此时 A A A的主合取范式为1)
- A A A为矛盾是当且仅当 A A A的主合取范式包含 2 n 2^{n} 2n个极大项
- A A A是可满足式时, A A A至少有一个成真赋值,因此 A A A的主合取范式极大项个数少于 2 n 2^{n} 2n
- 从极小项的角度
n n n元命题公式的主析取范式(主合取范式)的个数
- 根据排列组合可知,主析取范式和主合取范式的个数 N 1 , N 2 N_1,N_2 N1,N2相等,它们都可以从 n n n元极小项集合( N = 2 n N=2^{n} N=2n个元素)中抽取 0 ∼ 2 n 0\sim{2^{n}} 0∼2n个
- 因此都为 N 1 = N 2 = ∑ i = 0 N ( N i ) N_1=N_2=\sum_{i=0}^{N}\binom{N}{i} N1=N2=∑i=0N(iN)= ( 1 + 1 ) N (1+1)^{N} (1+1)N= 2 2 n 2^{2^n} 22n,则个数字和所有 n n n元命题公式的真值表个数相等
判断两个命题公式是否等值
- 设 A , B A,B A,B共有 n n n个命题变项,按 n n n个命题变项求出 A , B A,B A,B的主析取范式 A ′ , B ′ A',B' A′,B′,显然 A A A ⇔ \Leftrightarrow ⇔ A ′ A' A′ , B B B ⇔ \Leftrightarrow ⇔ B ′ B' B′
- 若 A ′ = B ′ A'=B' A′=B′,则 A A A ⇔ \Leftrightarrow ⇔ B B B,否则 A A A ⇎ \not\Leftrightarrow ⇔ B B B
给出一个满足给定真值表的命题公式
- 我们以半加器和全加器为例进行讨论相关算法
- 这部分涉及数字逻辑(数字电路逻辑,这门课很多内容是抽象数理逻辑具象化(或说知识应用))
- 数理逻辑中的真,假分别对应于数字电路逻辑中的二值(1,0)或高,低电平
- 我们的任务使从给定真值表通过一定的方法给出满足真值表的公式
半加器
-
例如二进制半加器(不考虑上一位的进位,但是考虑下一位进位;其输入变元 x , y x,y x,y其输出变元包含半 h h h和半进位 d d d),我们根据半加器的真值表来求取一个真值表和半加器相同的命题公式
-
x y 本位和位h 下一位进位d 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 -
分析此表,其包含了两个公式(输出半和位,半进位)
- x , y , h x,y,h x,y,h; x , y , d x,y,d x,y,d
-
下面我尝试给出主析取范式 h ( x , y ) h(x,y) h(x,y), d ( x , y ) d(x,y) d(x,y)
-
根据公式和其主范式的关系,如果要求主析取范式,则我们只需要关注真值表中的成真赋值
-
若想要求主合取范式
- 可以仅关注真值表中的成假赋值
- 也可以先求主析取范式,然后根据主合取范式和主析取范式的关系间接求得
-
x y h 0 0 0 0 1 1 1 0 1 1 1 0 -
x y d 0 0 0 0 1 0 1 0 0 1 1 1
-
-
h = m 1 ∨ m 2 h=m_1\vee{m_2} h=m1∨m2= ( ¬ x ∧ y ) ∨ ( x ∧ ¬ y ) (\neg{x}\wedge{y})\vee(x\wedge{\neg{y}}) (¬x∧y)∨(x∧¬y),
- 类似地可以求 h = M 0 ∧ M 3 h=M_0\wedge{M_3} h=M0∧M3= ( x ∨ y ) ∧ ( ¬ x ∨ ¬ y ) ({x}\vee{y})\wedge{(\neg{x}\vee{\neg{y}})} (x∨y)∧(¬x∨¬y)
-
d = m 3 d=m_{3} d=m3= x ∧ y x\wedge{y} x∧y;
- 类似地可以求得 d = M 0 ∧ M 1 ∧ M 2 d=M_0\wedge{M_1}\wedge{M_2} d=M0∧M1∧M2= ( x ∨ y ) ∧ ( x ∨ ¬ y ) ∧ ( ¬ x ∧ y ) (x\vee{y})\wedge{({x}\vee{\neg y})}\wedge{(\neg{x}\wedge{y})} (x∨y)∧(x∨¬y)∧(¬x∧y)
-
全加器
-
全加器不仅考虑了下一位的进位(carry out,简记为cout,或 c c c),同时考虑了上一位的进位
-
为此,输入也要有一个进位(carry in,简记为
cin,或 c ′ c' c′)来使上一位进位进入加法运算 -
1 , ⋯ , 2 n − 1 1,\cdots,{2^{n}-1} 1,⋯,2n−1 x y 上一位进位cin(c’) 本位和位s 下一位进位cout© 0 0 0 0 0 0 1 0 0 1 1 0 2 0 1 0 1 0 3 0 1 1 0 1 4 1 0 0 1 0 5 1 0 1 0 1 6 1 1 0 0 1 7 1 1 1 1 1 -
s s s= ( ¬ x ∧ ¬ y ∧ c ′ ) (\neg{x}\wedge{\neg y}\wedge{{c'}}) (¬x∧¬y∧c′) ∨ \vee ∨ ( ¬ x ∧ y ∧ ¬ c ′ ) (\neg{x}\wedge{y}\wedge{\neg c'}) (¬x∧y∧¬c′) ∨ \vee ∨ ( x ∧ ¬ y ∧ ¬ c ′ ) (x\wedge{\neg{y}}\wedge{\neg c'}) (x∧¬y∧¬c′) ∨ \vee ∨ ( x ∧ y ∧ c ′ ) (x\wedge{y}\wedge{c'}) (x∧y∧c′)
- = m 1 ∨ m 2 ∨ m 4 ∨ m 7 m_1\vee{m_2}\vee{m_4}\vee{m_{7}} m1∨m2∨m4∨m7
-
c c c= ( ¬ x ∧ y ∧ c ′ ) (\neg{x}\wedge{y}\wedge{{c'}}) (¬x∧y∧c′) ∨ \vee ∨ ( x ∧ ¬ y ∧ c ′ ) ({x}\wedge{\neg y}\wedge{c'}) (x∧¬y∧c′) ∨ \vee ∨ ( x ∧ y ∧ ¬ c ′ ) (x\wedge{{y}}\wedge{\neg c'}) (x∧y∧¬c′) ∨ \vee ∨ ( x ∧ y ∧ c ′ ) (x\wedge{y}\wedge{c'}) (x∧y∧c′)
- = m 3 ∨ m 5 ∨ m 6 ∨ m 7 m_3\vee{m_5}\vee{m_6}\vee{m_7} m3∨m5∨m6∨m7
半加器和全加器的联系
- 全加器可以由两个半加器和一个或门实现
- 设输入位为 x , y x,y x,y的半加器的本位和的函数表示 h ( x , y ) = ( ¬ x ∧ y ) ∨ ( x ∧ ¬ y ) h(x,y)=(\neg{x}\wedge{y})\vee(x\wedge{\neg{y}}) h(x,y)=(¬x∧y)∨(x∧¬y)(函数 h h h是异或门)
- 半进位 d ( x , y ) = x ∧ y d(x,y)=x\wedge{y} d(x,y)=x∧y(即与门)
- 则
- 全加器的本位和 s ( x , y , c ′ ) s(x,y,c') s(x,y,c′) ⇔ \Leftrightarrow ⇔ ( h ( x , y ) ∧ ¬ c ′ ) ∨ ( ¬ h ( x , y ) ∧ c ′ ) (h(x,y)\wedge{\neg{c'}})\vee{(\neg{h(x,y)}\wedge{c'})} (h(x,y)∧¬c′)∨(¬h(x,y)∧c′) ⇔ \Leftrightarrow ⇔ h ( h ( x , y ) , c ′ ) h(h(x,y),c') h(h(x,y),c′)
(1),异或门嵌套 - 下一位进位 c ( x , y , c ′ ) c(x,y,c') c(x,y,c′) ⇔ \Leftrightarrow ⇔ ( h ( x , y ) ∧ c ′ ) ∨ d ( x , y ) (h(x,y)\wedge{c'})\vee{d(x,y)} (h(x,y)∧c′)∨d(x,y) ⇔ \Leftrightarrow ⇔ d ( h ( x , y ) , c ′ ) ∨ d ( x , y ) d(h(x,y),c')\vee{d(x,y)} d(h(x,y),c′)∨d(x,y)
(2),其中 c ′ c' c′是全加器用来接受上一位进位的输入变量 - 根据
(1),容易仅需要两个半加器(分别记为半加器 a 1 , a 2 a_1,a_2 a1,a2)即可实现 s s s的计算- a 1 a_1 a1计算 h ( x , y ) h(x,y) h(x,y),同时提供 d ( x , y ) d(x,y) d(x,y)
- a 2 a_2 a2计算 h ( h ( x , y ) , c ′ ) h(h(x,y),c') h(h(x,y),c′),同时还提供 d ( x , y ) , d ( h ( x , y ) , c ′ ) d(x,y),d(h(x,y),c') d(x,y),d(h(x,y),c′)
(1.1)
- 根据
(1.1),(2),再加上一个或门就可以计算 c c c,
- 全加器的本位和 s ( x , y , c ′ ) s(x,y,c') s(x,y,c′) ⇔ \Leftrightarrow ⇔ ( h ( x , y ) ∧ ¬ c ′ ) ∨ ( ¬ h ( x , y ) ∧ c ′ ) (h(x,y)\wedge{\neg{c'}})\vee{(\neg{h(x,y)}\wedge{c'})} (h(x,y)∧¬c′)∨(¬h(x,y)∧c′) ⇔ \Leftrightarrow ⇔ h ( h ( x , y ) , c ′ ) h(h(x,y),c') h(h(x,y),c′)
- 所以两个半加器和一个或门即可实现全加器
- 至于半加器,可以使用一个异或门和与门实现(其中异或门可以由两个与门,两个非门和一个或门实现)
Note:
-
设半加器本位输出和 h = ( ¬ x ∧ y ) ∨ ( x ∧ ¬ y ) h=(\neg{x}\wedge{y})\vee(x\wedge{\neg{y}}) h=(¬x∧y)∨(x∧¬y);全加器下一位进位输出 s s s:
-
s s s ⇔ \Leftrightarrow ⇔ ( ¬ x ∧ ¬ y ∧ c ′ ) (\neg{x}\wedge{\neg y}\wedge{{c'}}) (¬x∧¬y∧c′) ∨ \vee ∨ ( ¬ x ∧ y ∧ ¬ c ′ ) (\neg{x}\wedge{y}\wedge{\neg c'}) (¬x∧y∧¬c′) ∨ \vee ∨ ( x ∧ ¬ y ∧ ¬ c ′ ) (x\wedge{\neg{y}}\wedge{\neg c'}) (x∧¬y∧¬c′) ∨ \vee ∨ ( x ∧ y ∧ c ′ ) (x\wedge{y}\wedge{c'}) (x∧y∧c′)
- ⇔ \Leftrightarrow ⇔ [ ( ( ¬ x ∧ ¬ y ) ∨ ( x ∧ y ) ) ∧ c ′ ] [((\neg x\wedge{\neg{y}})\vee({x}\wedge{y}))\wedge{c'}] [((¬x∧¬y)∨(x∧y))∧c′] ∨ \vee ∨ [ ( ( ¬ x ∧ y ) ∨ ( x ∧ ¬ y ) ) ∧ ¬ c ′ ] [((\neg{x}\wedge{y})\vee{(x\wedge{\neg y})})\wedge{\neg{c'}}] [((¬x∧y)∨(x∧¬y))∧¬c′]
- 再由分配律和德摩根,可知 w = ( ¬ x ∧ ¬ y ) ∨ ( x ∧ y ) w=(\neg x\wedge{\neg{y}})\vee({x}\wedge{y}) w=(¬x∧¬y)∨(x∧y)和 h = ( ¬ x ∧ y ) ∨ ( x ∧ ¬ y ) h=(\neg{x}\wedge{y})\vee{(x\wedge{\neg y})} h=(¬x∧y)∨(x∧¬y)是互非的关系: w = ¬ h w=\neg{h} w=¬h
- 从而 s s s ⇔ \Leftrightarrow ⇔ ( ¬ h ∧ c ′ ) ∨ ( h ∧ c ′ ) (\neg{h}\wedge{c'})\vee(h\wedge{c'}) (¬h∧c′)∨(h∧c′)
主范式合并化简
- 从主范式合并化简为尽可能简单的等价范式是重要问题
- 这个过程和主范式化的是互逆的过程
- 主范式的意义在于能够方便的比较两个公式是否等价以及其他真值表能够完成的任务
- 化简的意义在于,使公式更加简洁,从而在某些应用上更加方便和高效
- 比如涉及一个具有特定真值表的组合逻辑电路,公式越简单,所需要的基本逻辑门也就越少,布线和硬件成本也更低,功耗也更优
- 容易知道,化简得结果可能不唯一,但好的结果使项数尽可能少,每项的变元尽可能少
卡诺图法
- 在数字逻辑中,这个任务称为逻辑函数化简
- 有表格化方法,叫做卡诺图法,其借助格雷码设计而成,通过画卡诺圈来给出化简后的公式
- 这种方法有比较一般的步骤,但是对于变量数目多的(4个以上),就比较繁琐
- 也可用公式的运算律(等值式模式)作合并化简工作,这种方式对于基本功要求比较扎实
- 有表格化方法,叫做卡诺图法,其借助格雷码设计而成,通过画卡诺圈来给出化简后的公式
公式法
- 并项法: ( A ∧ B ) ∨ ( ¬ A ∧ B ) (A\wedge B)\vee(\neg{A}\wedge{B}) (A∧B)∨(¬A∧B) ⇔ \Leftrightarrow ⇔ B B B;该公式可以将两个与项合并为一个,并且消去其中的一个变量
- 吸收法: A ∨ ( A ∧ B ) A\vee (A\wedge B) A∨(A∧B) ⇔ \Leftrightarrow ⇔ A A A;吸收多余的与项
- 消去法: A ∨ ( ¬ A ∧ B ) A\vee(\neg{A}\wedge{B}) A∨(¬A∧B) ⇔ \Leftrightarrow ⇔ A ∨ B A\vee{B} A∨B;消去与项多余的因子
- 配项消项法: ( A ∧ B ) ∨ ( ¬ A ∧ C ) (A\wedge{B})\vee(\neg{A}\wedge{C}) (A∧B)∨(¬A∧C) ⇔ \Leftrightarrow ⇔ ( A ∧ B ) ∨ ( ¬ A ∧ C ) ∨ ( B ∧ C ) (A\wedge{B})\vee{(\neg{A}\wedge{C})}\vee{(B\wedge{C})} (A∧B)∨(¬A∧C)∨(B∧C)配项多出一个与项,尝试合并其他与项来消去更多与项
最简范式
- 最简主析取式(最简与或式):简单合取式个数最少(与项个数最少);简单合取式(与项)中变量个数最少
- 最简主合取式(最简或与式):简单析取式个数最少(或项个数最少);简单析取式(或项)中变量个数最少
相关文章:

DM@命题公式@主范式的性质和应用@数理逻辑解决数字电路全加器问题
文章目录 abstract主合取范式与主析取范式间的关系👺主范式存在及唯一性定理例 主范式的性质👺求公式的成真与成假赋值主析取范式直接得到主合取范式 判断公式的类型 n n n元命题公式的主析取范式(主合取范式)的个数判断两个命题公式是否等值 给出一个满…...
基于微信小程序+Springboot线上租房平台设计和实现【三端实现小程序+WEB响应式用户前端+后端管理】
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...
--IBERT)
Xilinx FPGA 7系列 GTX/GTH Transceivers (2)--IBERT
IBERT GTX IBERT核心提供了基础广泛的物理介质附件(PMA)评估7系列FPGA GTX收发器的演示平台。可参数化以使用不同GTX收发器和时钟拓扑,IBERT核心也可以定制使用不同的线速率、参考时钟速率和逻辑宽度。数据模式生成器和每个所需的GTX收发器都包含了检查程序,给出了几个不同…...

Python 文件介绍和正则表达式
文章目录 Python 文件和正则表达式文件打开文件读取文件直接读取 read():逐行读取采用 **for** 循环:采用 readlines(): 正则表达式匹配规则re 模块match 方法:search 方法group 方法split 方法编译:compile 方法 Pyth…...
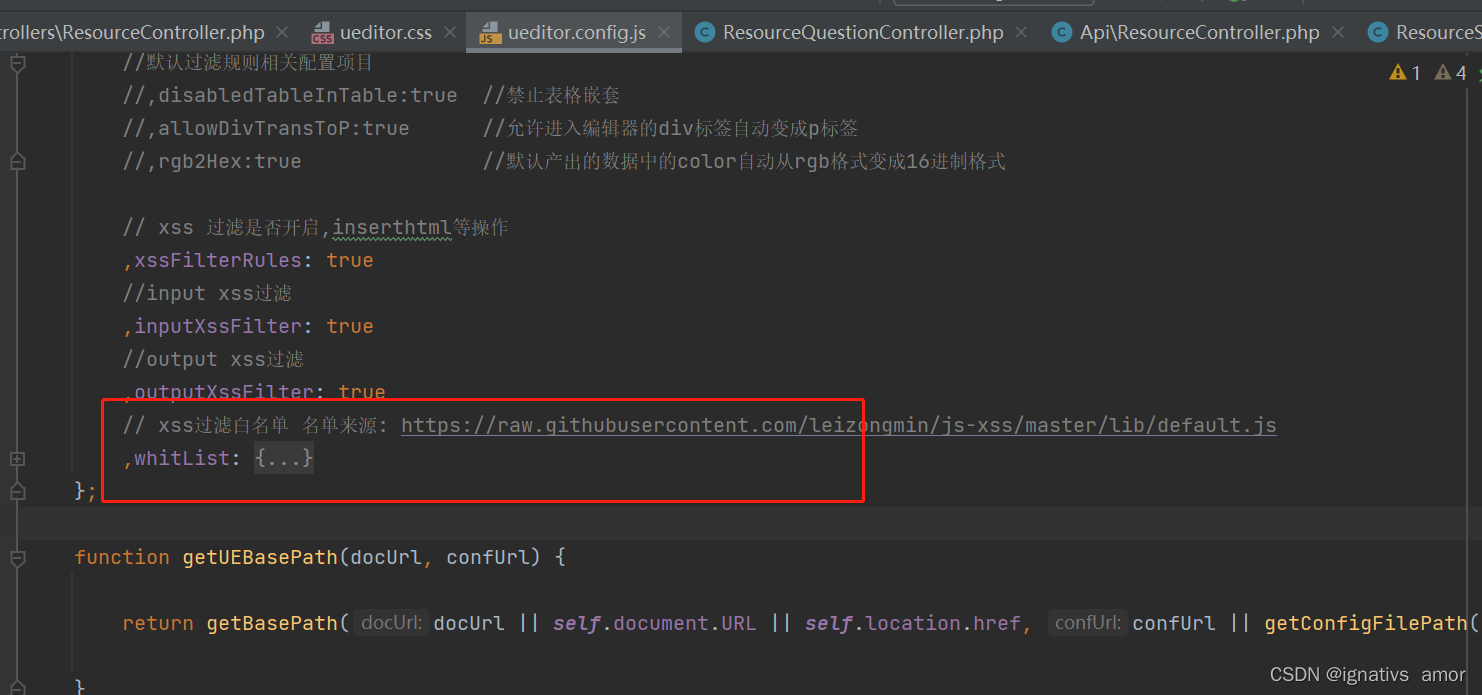
ueditor百度富文本编辑器粘贴后html丢失class和style样式
问题 项目经理从123在线编辑上排版好的文章,粘贴到项目的编辑器上,样式完全乱了, 排版是这样的: 复制到ueditor后的格式: 这天差地别呀,于是打开代码模式,发现section的属性全没了 但是,sp…...

人脸自动贴国旗
(一)简介 国庆快到了,每年这个时候,大家的头像都会贴上国旗水印,然后我就像这刚好可以用opencv dilb实现一个简单的自动将国旗贴在人脸上,刚好配合gradio写一个简单的demo gradio官方文档 (…...
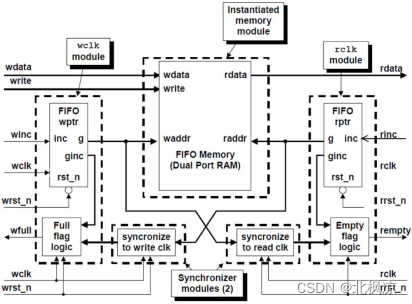
异步FIFO设计
1 FIFO简介 FIFO的本质是RAM,具有先进先出的特性。 FIFO的基本使用原则:空时不能读,满时不能写 FIFO的两个重要参数:宽度和深度 FIFO的两种类型: 同步FIFO:读写时钟相同,通常用来做数据缓存…...

学习python和anaconda的经验
PYTHON 1 常用命令 1.1 1.1 注释 Python注释多行的方法有以下三种:使用ctrl+/实现多行注释、在每一行的开头使用shift+#键、输入’‘’ ‘’或者"“” “”",将要注释的代码插在中间 1.2 def init( ):函数 区分两个函数: 1.def init(self): 这种形式在__init_…...

【Linux】多线程【上】
文章目录 前言1、Linux线程概念1-1、什么是线程?1-1-1、如何看待页表1-1-2、回顾进程地址空间1-1-3、页表怎么进行虚拟地址到物理地址的映射的?1-1-4、Linux中线程的概念(重点)1-1-5、原生线程库1-1-6、代码测试1-1-7、知识点&…...

生成式人工智能在高等教育 IT 中的作用
作者:Jared Pane 通过将你大学的数据与公共 LLMs 和 Elasticsearch 安全集成来找到你需要的答案。 根据 2023 年 4 月 EDUCAUSE 的一项调查,83% 的受访者表示,生成式人工智能将在未来三到五年内深刻改变高等教育。 学术界很快就询问和想象生…...

黑龙江省DCMM认证、CSMM认证、CMMM认证、知识产权等政策奖励
2023年8月28日 为深入落实党的二十大精神,认真落实省第十三次党代会关于创新龙江建设的部署要求,全面贯彻新发展理念,融入和服务构建新发展格局,实施创新驱动发展战略,着力建设创新龙江,不断塑造振兴发展新…...

腾讯云2023年云服务器优惠活动价格表
腾讯云经常推出各种云产品优惠活动,为了帮助大家更好地了解腾讯云服务器的价格和优惠政策,下面给大家分享腾讯云最新云服务器优惠活动价格表,助力大家轻松上云! 一、轻量应用服务器优惠活动价格表 1、轻量应用服务器:…...

Sleuth--链路追踪
1 链路追踪介绍 在大型系统的微服务化构建中,一个系统被拆分成了许多模块。这些模块负责不同的功能,组合成系统,最终可以提供丰富的功能。在这种架构中,一次请求往往需要涉及到多个服务。互联网应用构建在不同的软件模块集上&…...
MyBatis初级
文章目录 一、mybatis1、概念2、JDBC缺点2.1、之前jdbc操作2.2 、原始jdbc操作的分析 3、mybatis的使用3.1、导入maven依赖3.2、新建表3.3、实体类3.4、编写mybatis的配置文件3.5、编写接口 和 映射文件3.6、编写测试类3.7、注意事项 4、代理方式开发5、mybatis和spring整合5.1…...
AOP)
Spring 学习(二)AOP
一、什么是AOP Aspect Oriented Programming,即面向切面编程。对一个大型项目的代码而言,整个系统要求关注安全检查、日志、事务等功能,这些功能实际上“横跨”多个业务方法。在一般的OOP编程里,需要在每一个业务方法内添加相关非…...
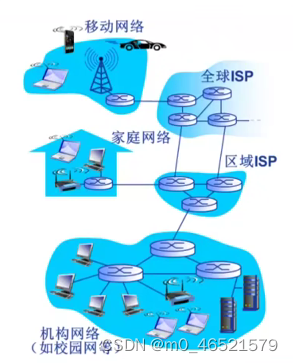
笔记1.1 计算机网络基本概念
计算机网络是通信技术与计算机技术紧密结合的产物 通信系统模型: 计算机网络是一种通信网络 计算机网络是互连的、自洽的计算机集合。 互连:互联互通 自洽:无主从关系 通过交换网络互连主机 Internet:数以百万计的互连的计算设…...

液压切管机配套用液压泵站比例阀放大器
液压切管机配套用液压泵站是液压系统的动力源,可按机械设备工况需要提供一定压力、流量和清洁度的工作介质。它由泵组、油箱组件、控温组件、滤油器组件及蓄能器组件等组合而成,液压泵站主要服务于大型管道工程。...

C++ Primer Plus 第七章笔记
目录 函数基本知识 没有返回值的函数:void函数 有返回值的函数: 函数原型 1.为什么需要函数原型? 2.函数原型的语法 3.函数原型的功能 按值传递函数参数 形参和实参 局部变量 参数问题 使用const指针参数 调用自身的函数…...
常用数据库的 API - 开篇
API API 这个词在大多数人看来可能和 CNS 差不多,前者天天听说就是用不上,后者天天读就是发不了。 不过,通过今天的一个简短介绍,今后 API 这个东西你就用上了,因为在文章最后我将会展示一个最最基础且高频的 API 使…...

C++之生成详细汇编代码(二百一十六)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
