回归与聚类算法系列④:岭回归
目录
1. 背景
2. 数学模型
3. 特点
4. 应用领域
5. 岭回归与其他正则化方法的比较
6、API
7、代码
8、总结
🍃作者介绍:双非本科大三网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅长web应用开发、数据结构和算法,初步涉猎Python人工智能开发。
🦅主页:@逐梦苍穹
📕回归与聚类算法系列
⭐①:概念简述
⭐②:线性回归
⭐③:欠拟合与过拟合
🍔您的一键三连,是我创作的最大动力🌹
岭回归(Ridge Regression)是线性回归的一种变体,它在专业统计和机器学习领域中应用广泛。岭回归的核心目标是解决线性回归中的过拟合问题,并提高模型的泛化性能。
1. 背景
岭回归最早由统计学家Arthur E. Hoerl和Robert W. Kennard于1970年提出,是为了解决多重共线性(Multicollinearity)问题而诞生的。多重共线性是指在线性回归中,自变量之间存在高度相关性的情况,这会导致模型参数的估计不稳定,降低了模型的解释性能。
2. 数学模型
岭回归与线性回归类似,但在损失函数中引入了L2正则化项,用于惩罚模型参数的大小。
岭回归的数学模型如下所示:
其中:
- yi 是观测数据点(目标变量)。
- xij 是输入特征矩阵的元素,表示第 i 个观测数据点的第 j 个特征。
- β0 和 βj 是模型的参数,需要估计。
- α 是岭回归的正则化参数,也称为正则化强度或惩罚参数。
损失函数的第一部分是最小二乘法的残差平方和,第二部分是L2正则化项。α是超参数,用于控制正则化的强度。较大的α值会导致模型参数趋于收缩,减小过拟合的风险。
3. 特点
- 解决多重共线性:岭回归可以处理自变量之间的高度相关性,使得模型参数估计更稳定。
- 增加模型复杂度:岭回归允许模型更复杂,因为正则化项允许参数取较大的值,但在不引入过拟合的情况下。
- 参数缩减:岭回归的正则化项会使一些参数趋于零,实现了参数缩减(Parameter Shrinkage)。
- 泛化能力提高:通过减小模型的方差,岭回归通常提高了模型在新数据上的泛化能力。
4. 应用领域
- 经济学:用于经济数据建模,以预测经济变量之间的关系。
- 生物统计学:用于基因表达分析和生物信息学领域,以处理高维数据。
- 工程学:用于工程建模和控制系统设计,以改善模型的鲁棒性。
- 金融学:用于资产定价和风险管理,以降低投资组合的风险。
5. 岭回归与其他正则化方法的比较
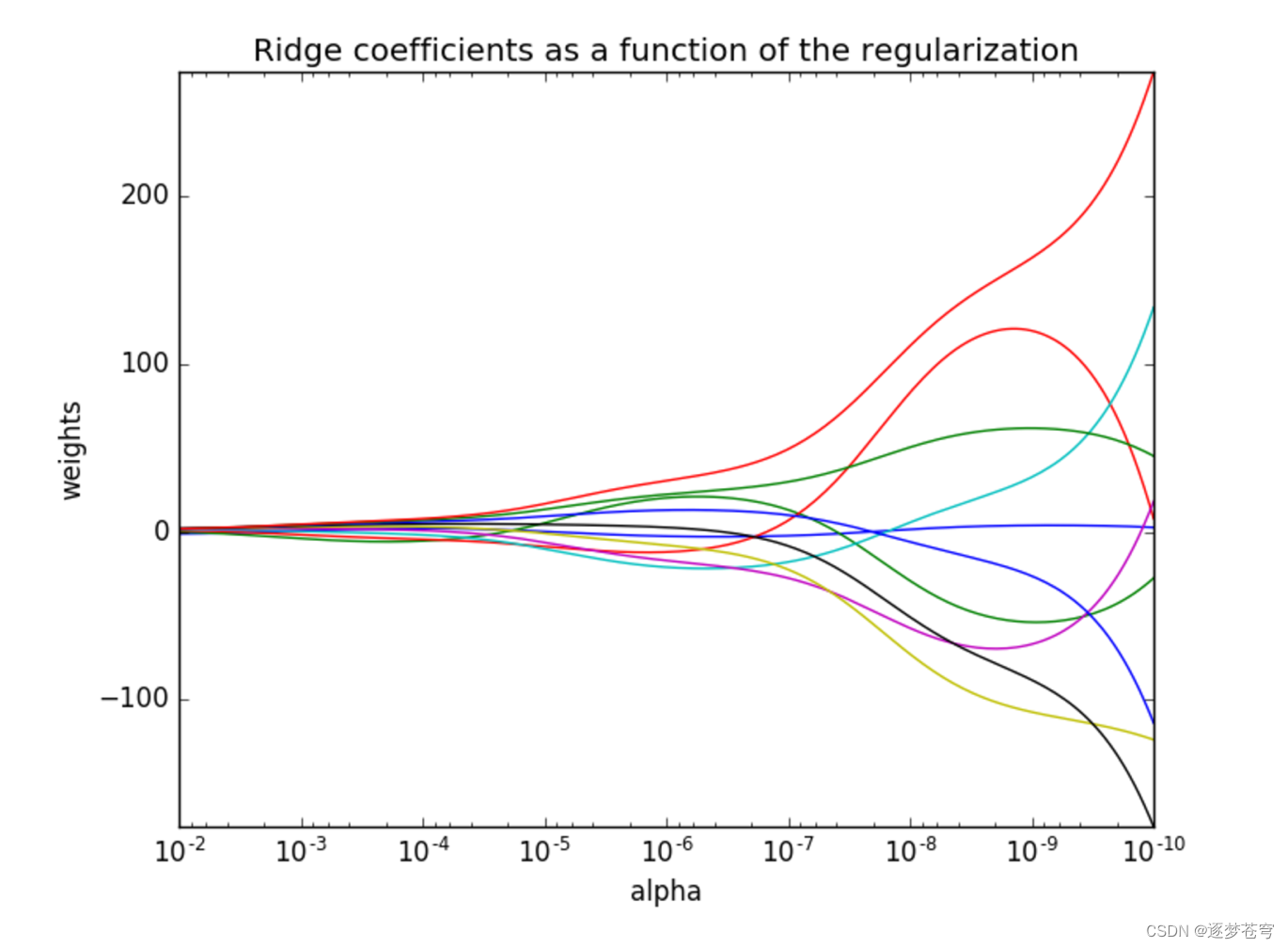
正则化力度越大,权重系数会越小
正则化力度越小,权重系数会越大
岭回归是一种L2则化方法,与L1正则化方法(如LASSO回归)不同,L1正则化可以导致参数稀疏性。选择哪种方法通常取决于具体问题和数据集的性质。
岭回归、LASSO回归和Elastic Net回归是三种常见的正则化线性回归方法,它们在处理多重共线性和过拟合问题时有不同的特点。下面是这三种方法之间的比较:
1. 岭回归(Ridge Regression):
- 正则化项: 岭回归使用L2正则化项,即对模型参数的平方和进行惩罚。
- 特点: 岭回归通过约束参数的平方和来控制参数的大小,使得模型参数趋于较小的值,但不会将参数压缩到零。
- 解决的问题: 主要用于解决多重共线性问题和过拟合问题,可以保留所有特征,但对它们的权重进行缩减。
- 稳定性: 对于高度相关的特征,岭回归能够给出相对稳定的参数估计。
- 适用场景: 适用于特征之间存在相关性,但不希望丢弃特征的情况。
2. LASSO回归(Least Absolute Shrinkage and Selection Operator):
- 正则化项: LASSO回归使用L1正则化项,即对模型参数的绝对值之和进行惩罚。
- 特点: LASSO回归倾向于将不重要的特征的参数压缩到零,从而实现特征选择(Feature Selection)。
- 解决的问题: 同样用于解决多重共线性和过拟合问题,但通常会导致一些特征的系数变为零,从而实现特征选择。
- 稳定性: 在存在高度相关的特征时,LASSO回归可能会随机选择其中一个特征。
- 适用场景: 适用于希望进行特征选择的情况,可以减少模型的复杂度。
3. Elastic Net回归:
- 正则化项: Elastic Net回归结合了L1正则化项和L2正则化项,同时对模型参数的绝对值和平方和进行惩罚。
- 特点: Elastic Net回归综合了岭回归和LASSO回归的优点,可以在解决多重共线性和过拟合问题的同时进行特征选择。
- 解决的问题: 适用于综合考虑多重共线性和特征选择的问题。
- 稳定性: 在存在高度相关的特征时,Elastic Net回归相对稳定,并可以选择一组相关性较高的特征。
- 适用场景: 适用于需要综合考虑多个因素的情况,既希望减少特征数又需要保留相关性高的特征。
选择合适的正则化方法通常取决于具体问题和数据集的性质。如果特征之间存在高度相关性,但不希望进行特征选择,岭回归可能是一个良好的选择。如果需要进行特征选择,LASSO回归或Elastic Net回归可能更合适。不同方法之间的超参数需要进行调优,以获得最佳模型性能。
6、API
sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)具有l2正则化的线性回归alpha:正则化力度,也叫 λλ取值:0~1 1~10solver:会根据数据自动选择优化方法sag:如果数据集、特征都比较大,选择该随机梯度下降优化normalize:数据是否进行标准化normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据Ridge.coef_:回归权重Ridge.intercept_:回归偏置All last four solvers support both dense and sparse data. However,
only 'sag' supports sparse input when `fit_intercept` is True.
这段话解释了关于使用不同优化方法时对稠密(dense)和稀疏(sparse)数据以及fit_intercept参数的支持情况。
首先,这里提到的四种优化方法是用于岭回归模型的优化方法。它们分别是:
- auto: 这个选项会根据数据的大小和特征数自动选择最适合的优化方法。
- sag: 随机平均梯度下降(Stochastic Average Gradient Descent)方法,通常用于处理大型数据集和特征数较多的情况。
- 其他两种方法未在这段话中详细说明。
然后,这段话指出,这四种优化方法都支持处理稠密和稀疏数据。稠密数据是指数据集中的大多数元素都是非零的,而稀疏数据是指数据集中的大多数元素都是零的。这些优化方法可以适用于两种类型的数据。
有一个例外情况:当设置fit_intercept=True时,只有sag方法支持处理稀疏数据。这是因为当fit_intercept为True时,模型需要估计偏置(intercept),而sag方法是唯一支持在这种情况下使用稀疏输入数据的方法。其他方法在这种情况下可能会导致错误或不稳定的行为。
因此,如果你的数据是稀疏的,并且你需要拟合一个带有偏置的岭回归模型,那么最好选择sag优化方法。如果你使用其他优化方法,并且希望处理稀疏数据,建议在调用岭回归之前使用preprocessing.StandardScaler等方法手动将数据标准化。
Ridge方法相当于SGDRegressor(penalty='l2', loss="squared_loss")。
只不过SGDRegressor实现了一个普通的随机梯度下降学习,推荐使用Ridge(实现了SAG)
sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)
具有l2正则化的线性回归,可以进行交叉验证
coef_:回归系数
class _BaseRidgeCV(LinearModel):def __init__(self, alphas=(0.1, 1.0, 10.0),fit_intercept=True, normalize=False, scoring=None,cv=None, gcv_mode=None,store_cv_values=False):7、代码
# -*- coding: utf-8 -*-
# @Author:︶ㄣ释然
# @Time: 2023/9/6 10:37
import warningsimport joblib
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler'''
sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)具有l2正则化的线性回归alpha:正则化力度,也叫 λλ取值:0~1 1~10solver:会根据数据自动选择优化方法sag:如果数据集、特征都比较大,选择该随机梯度下降优化normalize:数据是否进行标准化normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据Ridge.coef_:回归权重Ridge.intercept_:回归偏置
'''
def ridge():"""岭回归对波士顿房价进行预测:return:"""# 1)获取数据boston = load_boston()print("特征数量:\n", boston.data.shape)# 2)划分数据集x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)# 3)标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)# 4)预估器estimator = Ridge(alpha=0.5, max_iter=10000)estimator.fit(x_train, y_train)# 保存模型joblib.dump(estimator, "my_ridge.pkl")# 加载模型# estimator = joblib.load("my_ridge.pkl")# 5)得出模型print("岭回归-权重系数为:\n", estimator.coef_)print("岭回归-偏置为:\n", estimator.intercept_)# 6)模型评估y_predict = estimator.predict(x_test)print("预测房价:\n", y_predict)error = mean_squared_error(y_test, y_predict)print("岭回归-均方误差为:\n", error)if __name__ == '__main__':warnings.filterwarnings("ignore")ridge()8、总结
总之,岭回归是一种强大的工具,用于改善线性回归模型的性能,并处理多重共线性问题。它在各种领域中都有着广泛的应用,特别是在需要处理高维数据或自变量相关性较强的情况下,岭回归可以提供可靠的模型估计。
相关文章:

回归与聚类算法系列④:岭回归
目录 1. 背景 2. 数学模型 3. 特点 4. 应用领域 5. 岭回归与其他正则化方法的比较 6、API 7、代码 8、总结 🍃作者介绍:双非本科大三网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅长web应用开发、数…...
idea配置git(gitee)并提交(commit)推送(push)
Intellij Idea VCS | 版本控制 - 知乎 IDEA项目上传到gitee仓库_idea上传代码到gitee_robin19712的博客-CSDN博客 git程序下载国内镜像地址: https://registry.npmmirror.com/binary.html?pathgit-for-windows/v2.42.0.windows.2/ 解压后放到固定路径:…...

(19)Task异步:任务创建,返回值,异常捕捉,任务取消,临时变量
一、Task任务的创建 1、用四种方式创建,界面button,info各一。 程序代码 private void BtnStart_Click(object sender, EventArgs e){Task t new Task(() >{DisplayMsg($"[{Environment.CurrentManagedThreadId}]new Task.---1");});t.Start()…...
设备树的理解与运用
设备树: 本质是一个文件,包含很多节点,每个节点里边是对设备属性的描述(包括GPIO,时钟,中断等等),其中节点(node)和属性(property)就是设备树最重…...

【AIGC】提示词 Prompt 分享
提示词工程是什么? Prompt engineering(提示词工程)是指在使用语言模型进行生成性任务时,设计和调整输入提示(prompts)以改善模型生成结果的过程。它是一种优化技术,旨在引导模型产生更加准确、…...

【Axure视频教程】取整函数
今天教大家在Axure里如何使用三种不同的取整函数,包括向上取整、向下取整和四舍五入取整。具体效果可以参考下方视频。该教程从0开始制作,手把手教学,无论是新手小白还是有一定基础的同学,都可以学习的哦。 【视频教程——试看版…...

MySQL清空表
当我们需要清空一个表中的所有行时,除了使用 DELETE * FROM table 还可以使用 TRUNCATE TABLE 语句。 如果想要清空一个表, TRUNCATE TABLE 语句比 DELETE语句更加有效。 TRUNCATE TABLE 语法 TRUNCATE TABLE 的语法很简单,如下:…...

使用IDEA创建Vue3通过Vite实现工程化
1、创建Vite项目的分步说明 IntelliJ IDEA与Vite构建工具集成,改善了前端开发体验。Vite 由一个开发服务器和一个构建命令组成。构建服务器通过本机 ES 模块提供源文件。生成命令将代码与汇总捆绑在一起,汇总预配置为输出高度优化的静态资产以供生产。In…...

GitLab使用的最简便方式
GitLab介绍 GitLab是一个基于Git版本控制系统的开源平台,用于代码托管,持续集成,以及协作开发。它提供了一套完整的工具,以帮助开发团队协同工作、管理和部署代码。 往往在企业内部使用gitlab管理代码,记录一下将本地代…...

MySQL数据库20G数据迁移至其他服务器的MySQL库或者云MySQL库
背景:20G的MySQL数据迁移至火山云MySQL库,使用navicat的数据传输工具迁移速度耗费时间过长。 方案一:使用火山云提供的MySQL数据迁移服务(其他大厂应该提供的也有) 方案二:使用数据迁移工具kettle&#x…...

build.gradle配置文件详解
Andorid Studio高版本和低版本的build.gradle配置逻辑有些差异 安卓项目中相关编译文件的介绍 gradle-wrapper.properites:配置Gradle Wrapper gradle.properties:配置Gradle的编译参数。具体配置见Gradle官方文档:com.android.build.gradle | Andro…...
)
2024拼多多校招面试真题汇总及其解答(二)
6. 【算法题】归并排序 归并排序(Merge Sort)是一种分治算法,它将待排序的序列递归地分成两个子序列,然后将两个有序的子序列合并成一个有序的序列。 归并排序的算法流程如下: 递归地将待排序的序列分成两个子序列,直到每个子序列只有一个元素。将两个有序的子序列合并…...
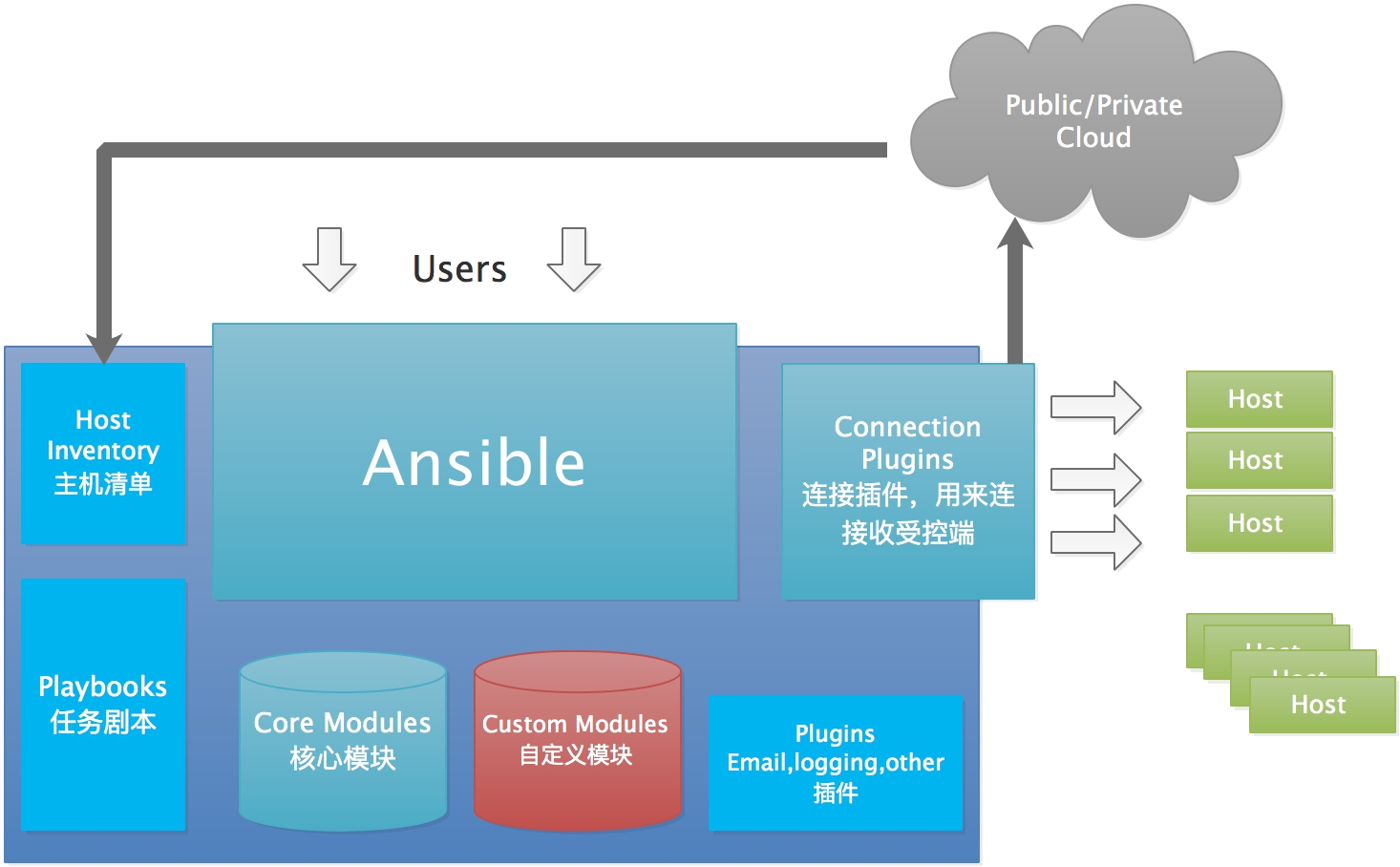
自动化运维工具Ansible教程(一)【入门篇】
文章目录 前言Ansible 入门到精通入门篇进阶篇精通篇入门篇1. Ansible 简介2. 安装 Ansible1. 通过包管理器安装:2. 通过源码安装: 3. Ansible 的基本概念和核心组件4. 编写和运行第一个 Ansible Playbook5. 主机清单和组织结构主机清单组织结构 6. Ansi…...

计算机毕业设计 微信小程序 uniapp+vue大学生兼职平台
任何系统都要遵循系统设计的基本流程,本系统也不例外,同样需要经过市场调研,需求分析,概要设计,详细设计,编码,测试这些步骤,本系统前台采用微信开发者结合后台Java语言设计并实现了…...

JavaScript框架:构建交互性、现代化Web应用的利器
💂 个人网站:【工具大全】【游戏大全】【神级源码资源网】🤟 前端学习课程:👉【28个案例趣学前端】【400个JS面试题】💅 寻找学习交流、摸鱼划水的小伙伴,请点击【摸鱼学习交流群】 引言 JavaScript框架已…...

数据结构——二分查找法
二分查找法(Binary Search)是一种高效的查找算法,通常用于在已排序的数组或列表中查找特定的目标值。这个算法的基本思想是不断将查找范围缩小为原来的一半,直到找到目标值或确定目标值不存在。 二分查找是一种在每次比较之后将查…...

服务端渲染(SSR):提升Web应用性能和用户体验的关键技术
💂 个人网站:【工具大全】【游戏大全】【神级源码资源网】🤟 前端学习课程:👉【28个案例趣学前端】【400个JS面试题】💅 寻找学习交流、摸鱼划水的小伙伴,请点击【摸鱼学习交流群】 引言 服务端渲染&#…...

如何工作和生活相平衡?
之前待过一家外企,他们的口号是 Balancing work and life,工作和生活相平衡。辗转几家公司之后,发现这个越来越难了,越来越少的时间投入家庭和自己的生活。 人生的意义 (AI) 人生的意义是一个深奥而复杂的…...

semaphere部署,配置ldap
在处理 Ansible 相关项目时,我们经常面临繁琐的命令行操作,这对于不熟悉命令行的用户来说可能是一个挑战。此外,当项目规模扩大时,跟踪和管理多个 playbook 变得困难,同时缺乏对失败的及时通知和访问控制。这些问题催生…...

Java 泛型 T,E,K,V,?
泛型带来的好处 在没有泛型的情况的下,通过对类型 Object 的引用来实现参数的“任意化”,“任意化”带来的缺点是要做显式的强制类型转换,而这种转换是要求开发者对实际参数类型可以预知的情况下进行的。对于强制类型转换错误的情况…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...
