1397: 图的遍历——广度优先搜索
题目描述
输入
输出
样例输入
0 0 0 1
0 0 1 1
0 1 0 1
1 1 1 0样例输出
0 3 1 2
提示
#include<bits/stdc++.h>
using namespace std;
const int N = 55;
struct Graph{//邻接表存储 int vnum;//图中结点个数 vector<int>e[N];//行不可变,列可变的二维数组
};
bool vis[N];//访问标记数组,用于标记已经访问过的结点void bfs(Graph &G,int x){//从图中结点x开始遍历 queue<int>q;//bfs需要有队列来辅助遍历q.push(x);vis[x]=1;//在入队的时候就要把当前访问的结点x标记为已访问while(q.empty()==false){//队列非空时,继续访问,等价写法while(!q.empty())int p = q.front();//p赋值为当前队列的队头结点的值 q.pop();//将队头结点出队printf("%d ",p); for(int i=0;i<G.e[p].size();++i){//扫描遍历p结点的所有邻接点,即队头结点的所有邻接点 if(vis[G.e[p][i]]==0){//如果当前结点没有被访问过,则入队并标记为已访问 q.push(G.e[p][i]);//在入队的时候就要把入队的结点标记为已访问,目的是为了防止后续结点有相同的邻接点时造成重复入队 vis[G.e[p][i]]=1;//G.e[p][i]表示邻接表G的第p行,第i列的结点,即p的第i个邻接点 }}}
}
void bfsTravel(Graph &G){memset(vis,0,sizeof(vis));//初始化访问数组(如果有多组测试输入一定要初始化)for(int i=0;i<G.vnum;++i){if(!vis[i]){bfs(G,i);}}
}
int main(void){Graph G;scanf("%d",&G.vnum);//输入结点个数 for(int i=0;i<G.vnum;++i){for(int j=0;j<G.vnum;++j){int flag;scanf("%d",&flag);if(flag==1){//如果输入为1,则说明e[i][j]存在无向边 G.e[i].push_back(j);//在邻接表第i行后面加上一个j,表示i和j有边 //此操作相当于邻接矩阵输入直接转换成邻接表 }}}bfsTravel(G);return 0;
}相关文章:

1397: 图的遍历——广度优先搜索
题目描述 广度优先搜索遍历类似于树的按层次遍历的过程。其过程为:假设从图中的某顶点v出发,在访问了v之后依次访问v的各个未曾被访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使“先被访问的顶点的邻接点”先…...
Java 华为真题-选修课
需求: 现有两门选修课,每门选修课都有一部分学生选修,每个学生都有选修课的成绩,需要你找出同时选修了两门选修课的学生,先按照班级进行划分,班级编号小的先输出,每个班级按照两门选修课成绩和的…...

Invalid access token: Invalid header string: ‘utf-8‘ codec can‘t decode byte
报错:在运行一个txt文档时报Invalid access token: Invalid header string: ‘utf-8’ codec can’t decode byte 原因:文档编码方式的原因,电脑默认的是UFT-8格式的编码 解决方法:用notepad改一下文档编码就好...

Java 中将多个 PDF 文件合并为一个 PDF
一.前言 我们将从以下两个方面向您展示如何将多个PDF文件合并为一个PDF: 1. 将文件中的多个 PDF 合并为单个 PDF 2. 将流中的多个 PDF 合并为单个 PDF 1. 了解 Spire.PDF 库 要在 Java 中合并 PDF 文件,我们将使用Spire.PDF 库。Spire.PDF for Java 是…...

python经典百题之水仙花数
题目:打印出所有的“水仙花数”,所谓“水仙花数”是指一个三位数,其各位数字立方和等于该数 本身。例如:153是一个“水仙花数”,因为1531的三次方+5的三次方+3的三次方。 方法一:暴…...

jvm的调优工具
1. jps 查看进程信息 2. jstack 查看进程的线程 59560为进程id 产生了死锁就可以jstack查看了 详细用途可以看用途 3. jmap 如何使用dump文件看下 查看 4.jstat 空间占用和次数 5. jconsole可视化工具 各种使用情况,以及死锁检测 6. visualvm可视化工具…...
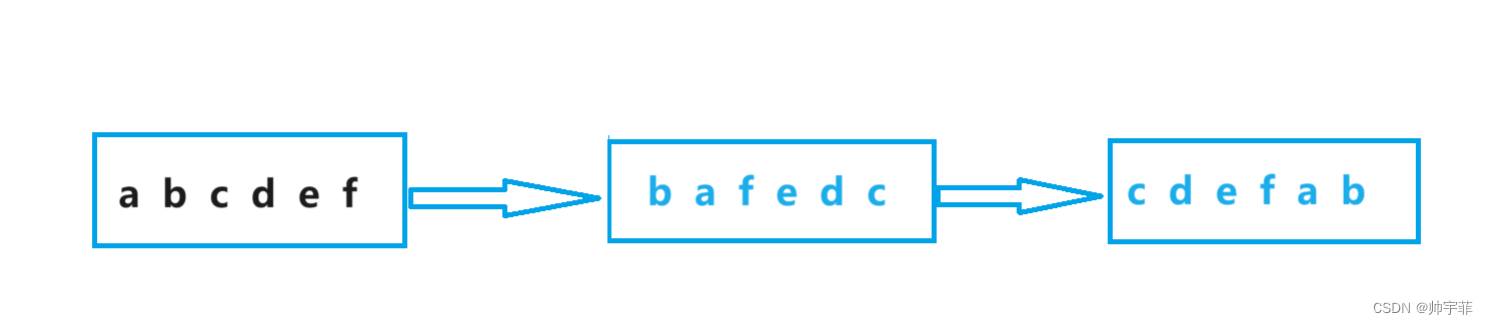
C语言--字符串旋转笔试题
C语言–字符串旋转笔试题 文章目录 C语言--字符串旋转笔试题一、字符串左旋1.1 思路11.2 思路1代码1.3 思路21.4 思路2代码 二、字符串旋转结果判断2.1 思路12.2 思路2 一、字符串左旋 实现一个函数,可以左旋字符串中的k个字符。 例如: ABCD左旋一个字…...
IntelliJ IDEA使用_常规设置
文章目录 版本说明主题设置取消检查更新依赖自动导入禁止import xxx.*、允许import内部类显示行号、方法分割线、空格代码提示(匹配所有字母)自定义注释颜色添加头部注释自定义字体设置字符编码关联本地GitJDK编译版本Maven配置Tomcat配置代码注释设置头…...

ResponseBodyAdvice 获取参数
废话不多说,简练,一针见血,解决问题,才是最好的。 首先肯定是重写了这个beforeBodyWrite方法 重点来了,获取请求参数: request.getBody()返回一个inputStream流,这里你可以 使用很多方法把这个…...

人力资源服务升级正当时,法大大助力佩信集团加速数字化
人力资源服务业是现代服务业的一个重要门类,在促进就业创业、提供人才服务方面发挥重要作用。同时面对产业转型升级、平台经济快速发展、企业用工成本提高等新形势,发展人力资源服务业对于促进社会化就业、更好发挥我国人力资源优势、服务经济社会发展具…...
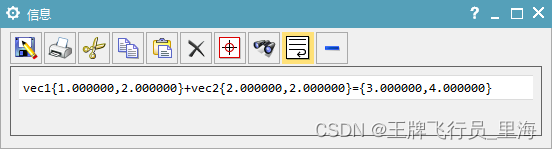
UG\NX二次开发 二维向量相加
文章作者:里海 来源网站:王牌飞行员_里海_里海NX二次开发3000例,里海BlockUI专栏,C\C++-CSDN博客 简介: UG\NX二次开发 二维向量相加 效果: 代码: #include "me.hpp"void doIt() {const double vec1[2] = { 1.0,2.0 };const double vec2[2] = { 2.0,2.…...

RabbitMQ深入 —— 持久化和发布确认
前言 前面的文章荔枝梳理了如何去配置RabbitMQ环境并且也介绍了两种比较简单的运行模式,在这篇文章中荔枝将会继续梳理有关RabbitMQ的持久化机制以及发布确认模式的相关知识,希望能够帮助到大家~~~ 文章目录 前言 一、持久化 1.1 队列持久化 1.2 消息…...

人脸识别三部曲
人脸识别三部曲 首先看目录结构图像信息采集 采集图片.py模型训练 训练模型.py人脸识别 人脸识别.py效果 首先看目录结构 引用文121本 opencv │ 采集图片.py │ 训练模型.py │ 人脸识别.py │ └───trainer │ │ trainer.yml │ └───data │ └──…...
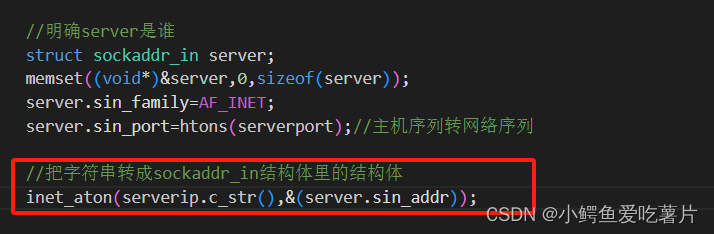
【Linux网络编程】Socket-TCP实例
netstat -nltp 无法用read函数读取UDP套接字的数据,因为UDP是面向数据报,而TCP是面向数据流。 客户端不需要 bind,listen,accept,但是客户端需要connect,connect会自动做bind工作。 #include <sys/sock…...

<OpenCV> 边缘填充
OpenCV边缘填充 1、边缘填充类型 enum cv::BorderTypes ORDER_CONSTANT iiiiii|abcdefgh|iiiiiii with some specified i -常量法,常熟值填充; BORDER_REPLICATE aaaaaa|abcdefgh|hhhhhhh -复制法,复制边缘像素; BORDER_R…...
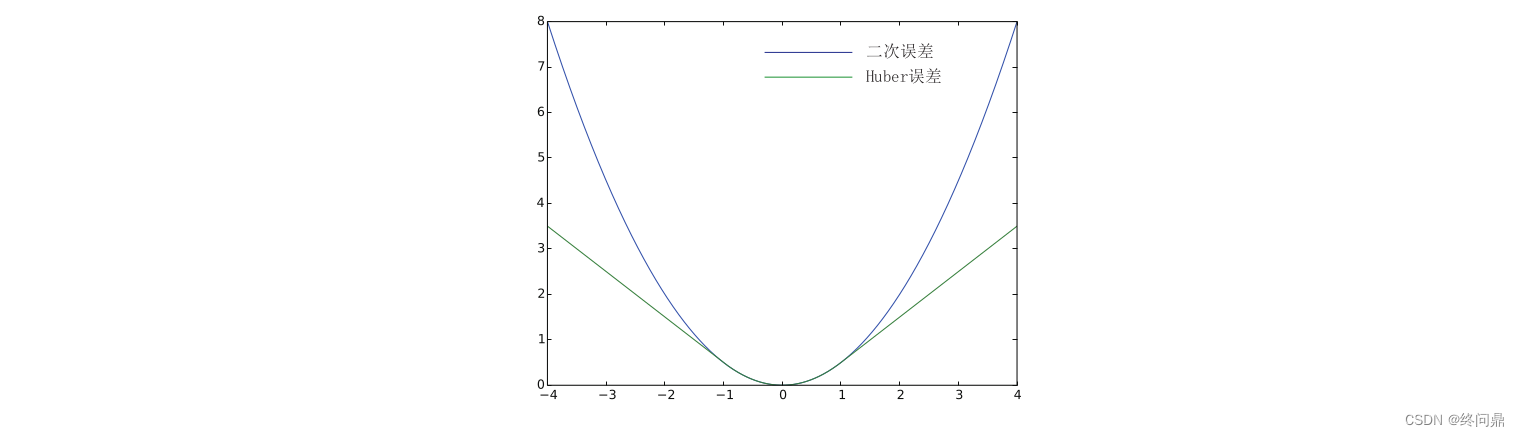
【视觉SLAM入门】7.3.后端优化 基于KF/EKF和基于BA图优化的后端,推导及举例分析
"时间倾诉我的故事" 1. 理论推导2. 主流解法3. 用EKF估计状态3.1. 基于EKF代表解法的感悟 4. 用BA法估计状态4.1 构建最小二乘问题4.2 求解BA推导4.3 H的稀疏结构4.4 根据H稀疏性求解4.5 鲁棒核函数4.6 编程注意 5.总结 引入: 前端里程计能给出一个短时间…...
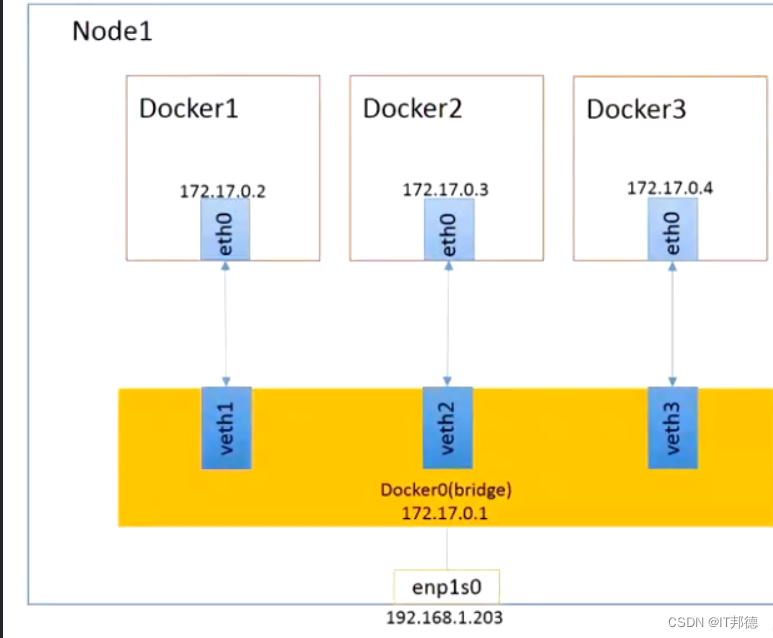
Docker概念通讲
目录 什么是Docker? Docker的应用场景有哪些? Docker的优点有哪些? Docker与虚拟机的区别是什么? Docker的三大核心是什么? 如何快速安装Docker? 如何修改Docker的存储位置? Docker镜像常…...

PHP请求API接口案例采集电商平台数据获取淘宝/天猫优惠券查询示例
优惠券查询API接口对于用户和商家来说具有重要作用,可以方便地获取优惠券信息,进行优惠券搜索和筛选,参与活动和促销推广,提供数据分析和决策支持,提升用户体验和忠诚度,为商家增加销售额和市场竞争力。 t…...
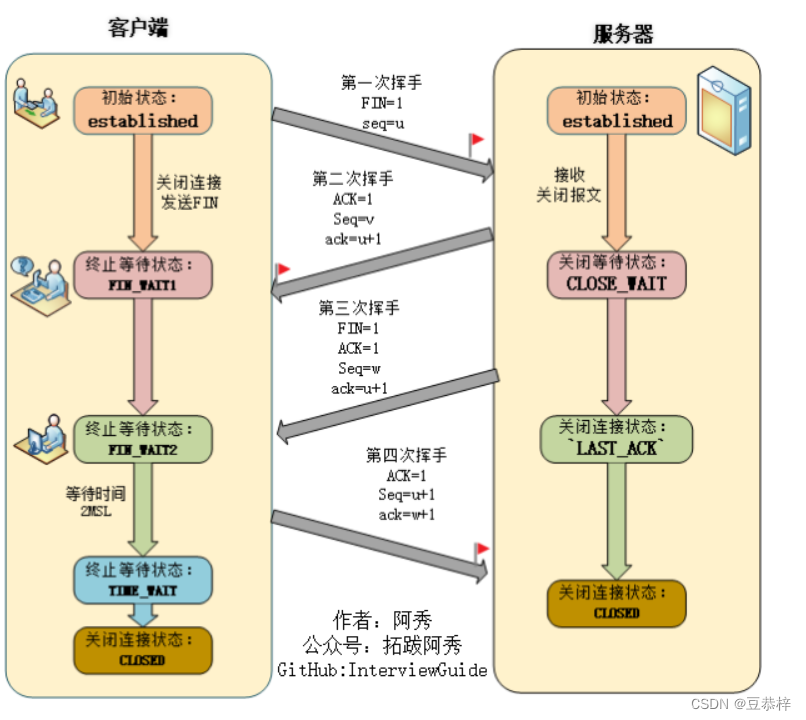
计算机网络:三次握手与四次挥手
摘取作者:拓跋阿秀 三次握手 三次握手(Three-way Handshake)其实就是指建立一个TCP连接时,需要客户端和服务器总共发送3个包。进行三次握手的主要作用就是为了确认双方的接收能力和发送能力是否正常、指定自己的初始化序列号为后…...
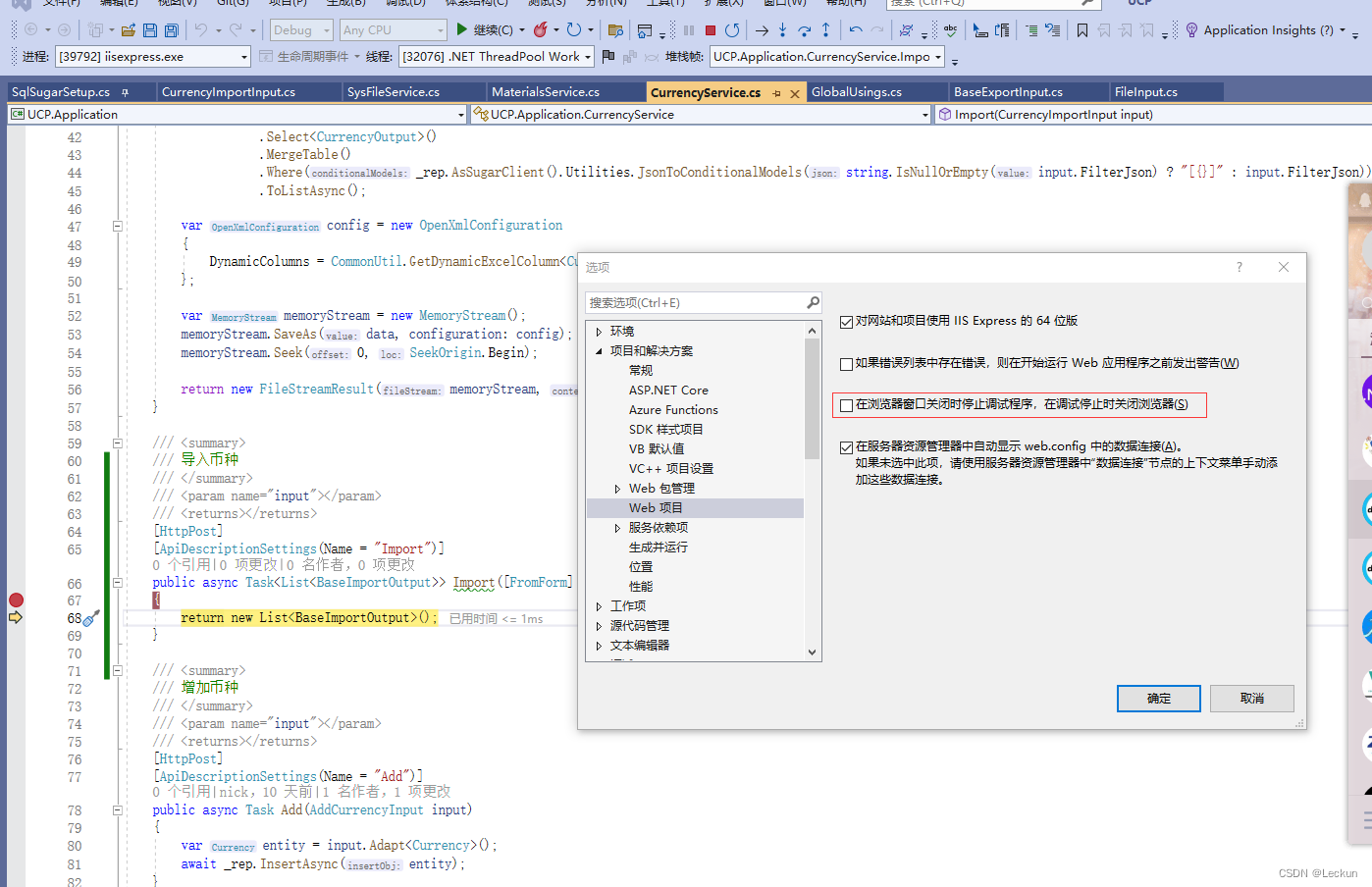
Visual Studio 调试上传文件时自动停止运行的解决方法
进入:选项,项目和解决方案,Web项目, 找到在浏览器窗口关闭时停止调试程序,在调试停止时关闭浏览器 将它不要勾关闭,然后重新启动下Visual Studio,上传文件时就可以调试了...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
