<图像处理> 空间滤波基础二
空间滤波基础二:锐化
锐化的作用的突出灰度中的过渡。图像锐化通过空间微分来实现,微分将增强边缘和其他不连续(噪声),不强化灰度变化缓慢的区域。图像锐化也叫做高通滤波,通过高频,抑制低频。
1、二阶导数锐化
f ( x ) f(x) f(x)的二阶导数定义为差分
∂ 2 f ∂ x 2 = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x ) \frac{\partial^2f}{\partial x^2}=f(x+1)+f(x-1)-2f(x) ∂x2∂2f=f(x+1)+f(x−1)−2f(x)
拉普拉斯滤波器
最简单的各向同性二阶导数核是拉普拉斯核,对于图像 f ( x , y ) f(x,y) f(x,y),其定义如下:
∇ 2 f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 \nabla^2 f=\frac{\partial^2f}{\partial x^2}+\frac{\partial^2f}{\partial y^2} ∇2f=∂x2∂2f+∂y2∂2f
由于任意阶的导数都是线性算子,所以拉普拉斯也是线性算子。如下是对上式的 x 、 y x、y x、y两个方向的离散化:
x x x方向:
∂ 2 f ∂ x 2 = f ( x + 1 , y ) + f ( x − 1 , y ) − 2 f ( x , y ) \frac{\partial^2f}{\partial x^2}=f(x+1,y)+f(x-1,y)-2f(x,y) ∂x2∂2f=f(x+1,y)+f(x−1,y)−2f(x,y)
y y y方向:
∂ 2 f ∂ y 2 = f ( x , y + 1 ) + f ( x , y − 1 ) − 2 f ( x , y ) \frac{\partial^2f}{\partial y^2}=f(x,y+1)+f(x,y-1)-2f(x,y) ∂y2∂2f=f(x,y+1)+f(x,y−1)−2f(x,y)
由上面三个公式可得,
∇ 2 f = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) \nabla^2 f=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) ∇2f=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)
由上式可得其卷积核如下:
[ 0 1 0 1 − 4 1 0 1 0 ] \begin{bmatrix} 0 & 1&0\\ 1 & -4&1 \\0 &1&0\\ \end{bmatrix} 0101−41010
更多变体:
(1) [ 1 1 1 1 − 8 1 1 1 1 ] \begin{bmatrix} 1 & 1&1\\ 1 & -8&1 \\1 &1&1\\ \end{bmatrix} 1111−81111 ,(2) [ 0 − 1 0 − 1 4 − 1 0 − 1 0 ] \begin{bmatrix} 0 & -1&0\\ -1 & 4&-1 \\0 &-1&0\\ \end{bmatrix} 0−10−14−10−10 ,(3) [ − 1 − 1 − 1 − 1 8 − 1 − 1 − 1 − 1 ] \begin{bmatrix} -1 & -1&-1\\ -1 & 8&-1 \\-1 &-1&-1\\ \end{bmatrix} −1−1−1−18−1−1−1−1
综上,卷积核(1)增加了±45°方向,(2)&(3)仅为符号的差异,产生的效果相同,但是需要注意当拉普拉斯滤波过后的图像与原图进行加减操作时的符号差异。
OpenCV函数:
void cv::Laplacian(InputArray src, OutputArray dst, int ddepth, int ksize = 1, double scale = 1, double delta = 0, int borderType = BORDER_DEFAULT) Parameters
src Source image.
dst Destination image of the same size and the same number of channels as src .
ddepth Desired depth of the destination image, see combinations.
ksize Aperture size used to compute the second-derivative filters. See getDerivKernels for details. The size must be positive and odd.
scale Optional scale factor for the computed Laplacian values. By default, no scaling is applied. See getDerivKernels for details.
delta Optional delta value that is added to the results prior to storing them in dst .
borderType Pixel extrapolation method, see BorderTypes. BORDER_WRAP is not supported.
2、 一阶导数锐化
f ( x ) f(x) f(x)的一阶导数定义为差分
∂ f ∂ x = f ( x + 1 ) − f ( x ) \frac{\partial f}{\partial x}=f(x+1)-f(x) ∂x∂f=f(x+1)−f(x)
在图像处理中,一阶导数是用梯度幅度实现的。图像f在(x,y)处的梯度定位为二维列向量
∇ f = g r a d ( f ) = [ g x g y ] = [ ∂ f ∂ x ∂ f ∂ y ] \nabla f=grad(f)=\begin{bmatrix}g_x\\ g_y \end{bmatrix}=\begin{bmatrix} \frac {\partial f}{\partial x} \\ \\\frac {\partial f} {\partial y} \end{bmatrix} ∇f=grad(f)=[gxgy]= ∂x∂f∂y∂f
向量 ∇ f \nabla f ∇f的幅度表示为 M ( x , y ) M(x,y) M(x,y),其中
M ( x , y ) = ∥ f ∥ = m a g ( ∇ f ) = g x 2 + g y 2 M(x,y)=\parallel f \parallel=mag(\nabla f)=\sqrt{g_x^2+g_y^2} M(x,y)=∥f∥=mag(∇f)=gx2+gy2
在某些实现中,使用绝对值来近似平方运算和平方根的运算,
M ( x , y ) ≈ ∣ g x ∣ + ∣ g y ∣ M(x,y)\approx |g_x|+|g_y| M(x,y)≈∣gx∣+∣gy∣
M ( x , y ) M(x,y) M(x,y)图像与原图尺寸大小相同,对应原图所有像素位置上的变化,该图像又叫做梯度图像。
离散的一阶导数卷积核有如下:
1、Roberts滤波器
Roberts算子的原理是通过计算对角方向相邻两个像素之差来计算图像的梯度大小和方向。梯度大小表示边缘的强度,梯度方向与边缘的走向垂直。
Roberts算法在边缘定位方面较为准确,但对噪声比较敏感,无法有效抑制噪声的影响。因此,它常被用于检测边缘明显、亮度差异较大的低噪声图像。
计算方式:
计算45°方向: g x ( x , y ) = f ( x + 1 , y ) − f ( x , y + 1 ) g_x(x,y)=f(x+1,y)-f(x,y+1) gx(x,y)=f(x+1,y)−f(x,y+1),滤波核如下:
M x = [ 0 1 − 1 0 ] M_x=\begin{bmatrix} 0 & 1\\ -1 & 0 \\ \end{bmatrix} Mx=[0−110]
计算135°方向, g y ( x , y ) = f ( x , y ) − f ( x + 1 , y + 1 ) g_y(x,y)=f(x,y)-f(x+1,y+1) gy(x,y)=f(x,y)−f(x+1,y+1),滤波核如下:
M y = [ 1 0 0 − 1 ] M_y=\begin{bmatrix} 1 & 0\\ 0 & -1 \\ \end{bmatrix} My=[100−1]
2、Prewitt滤波器
Prewitt算子利用像素点上下左右邻点的灰度差,在边缘处达到极值来检测边缘,对噪声具有平滑的作用。Prewitt算子同样也是一种基于局部差分计算的算法,由两个 3 ∗ 3 3*3 3∗3的模板组成,一个模板用于计算水平方向的梯度,另一个用于计算垂直方向的梯度。与Roberts算子相比,Prewitt算子的检测效果更加准确,仅稍微增加一些计算量就可以抑制噪音的影响。但是相较于Sobel算子和Laplacian算子,Prewitt算子的边缘检测效果较差。
M x = [ − 1 0 1 − 1 0 1 − 1 0 1 ] M_x=\begin{bmatrix} -1 & 0&1\\ -1 & 0&1 \\-1&0&1\\ \end{bmatrix} Mx= −1−1−1000111
M y = [ 1 1 1 0 0 0 − 1 − 1 1 ] M_y=\begin{bmatrix} 1 & 1&1\\ 0 & 0&0 \\-1&-1&1\\ \end{bmatrix} My= 10−110−1101
3、Sobel滤波器
Sobel算子可以在边缘检测时可以提供较为精确的边缘方向信息,对于噪声也具有一定的平滑作用。Sobel算子可以通过像素点上下、左右邻点灰度加权差,在边缘处达到极值这一现象检测边缘,是高斯平滑和微分求导的联合运算,抗噪声能力强。考虑了距离对权值的影响,距离越远的像素的影响越小。可以通过快速卷积实现,简单有效,应用广泛。
M x = [ − 1 0 1 − 2 0 2 − 1 0 1 ] M_x=\begin{bmatrix} -1 & 0&1\\ -2 & 0&2 \\-1&0&1\\ \end{bmatrix} Mx= −1−2−1000121
M y = [ 1 2 1 0 0 0 − 1 − 2 1 ] M_y=\begin{bmatrix} 1 & 2&1\\ 0 & 0&0 \\-1 &-2&1\\ \end{bmatrix} My= 10−120−2101
void cv::Sobel(InputArray src, OutputArray dst, int ddepth, int dx, int dy, int ksize = 3, double scale = 1, double delta = 0, int borderType = BORDER_DEFAULT) Parameters
src input image.
dst output image of the same size and the same number of channels as src .
ddepth output image depth, see combinations; in the case of 8-bit input images it will result in truncated derivatives.
dx order of the derivative x.
dy order of the derivative y.
ksize size of the extended Sobel kernel; it must be 1, 3, 5, or 7.
scale optional scale factor for the computed derivative values; by default, no scaling is applied (see getDerivKernels for details).
delta optional delta value that is added to the results prior to storing them in dst.
borderType pixel extrapolation method, see BorderTypes. BORDER_WRAP is not supported.
4、Scharr滤波器
Scharr算子是对Sobel算法的改进和增强。Scharr算子和Sobel算子在边缘检测原理和使用方式上基本相同。Scharr算子使用 3 ∗ 3 3*3 3∗3的滤波器,通过增大像素值间的差异来检测图像的边缘。它在X方向和Y方向上都有对应的边缘检测算子。
相比于Sobel算子,Scharr算子在权重系数上有所调整,使得其在图像梯度的计算中更为敏感。具体来说,Scharr算子使用的权重系数相对Sobel算子更大,以增强梯度的响应。这使得Scharr算子在对边缘进行检测时具有更好的精度和效果。
M x = [ − 3 0 3 − 10 0 10 − 3 0 3 ] M_x=\begin{bmatrix} -3 & 0&3\\ -10 & 0&10 \\-3&0&3\\ \end{bmatrix} Mx= −3−10−30003103
M y = [ 3 10 3 0 0 0 − 3 − 10 3 ] M_y=\begin{bmatrix} 3 & 10&3\\ 0 & 0&0 \\-3 &-10&3\\ \end{bmatrix} My= 30−3100−10303
void cv::Scharr (InputArray src, OutputArray dst, int ddepth, int dx, int dy, double scale = 1, double delta = 0, int borderType = BORDER_DEFAULT) Parameters
src input image.
dst output image of the same size and the same number of channels as src.
ddepth output image depth, see combinations
dx order of the derivative x.
dy order of the derivative y.
scale optional scale factor for the computed derivative values; by default, no scaling is applied (see getDerivKernels for details).
delta optional delta value that is added to the results prior to storing them in dst.
borderType pixel extrapolation method, see BorderTypes. BORDER_WRAP is not supported.
相关文章:

<图像处理> 空间滤波基础二
空间滤波基础二:锐化 锐化的作用的突出灰度中的过渡。图像锐化通过空间微分来实现,微分将增强边缘和其他不连续(噪声),不强化灰度变化缓慢的区域。图像锐化也叫做高通滤波,通过高频,抑制低频。…...

Java中的队列Queue
Queue(队列)是一种在计算机科学中常见的数据结构,它基于先进先出(FIFO)的原则,即最先进入队列的元素最先出队。在Java中,Queue是一个接口,定义了一组操作队列的方法,而具体的实现类可以选择性地实现这些方法。 以下是Queue的一些常见用途和操作: 添加元素: 使用off…...
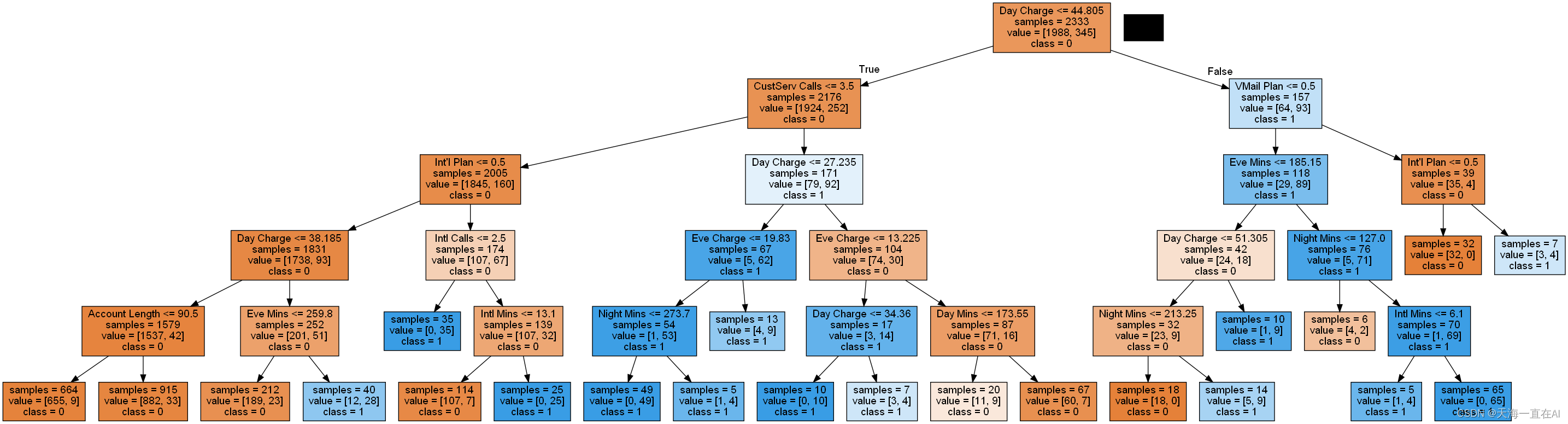
机器学习技术(十)——决策树算法实操,基于运营商过往数据对用户离网情况进行预测
机器学习技术(十)——决策树算法实操 文章目录 机器学习技术(十)——决策树算法实操一、引言二、数据集介绍三、导入相关依赖库四、读取并查看数据1、读取数据2、查看数据 五、数据预处理1、选择数据2、数据转码 六、建模与参数优…...
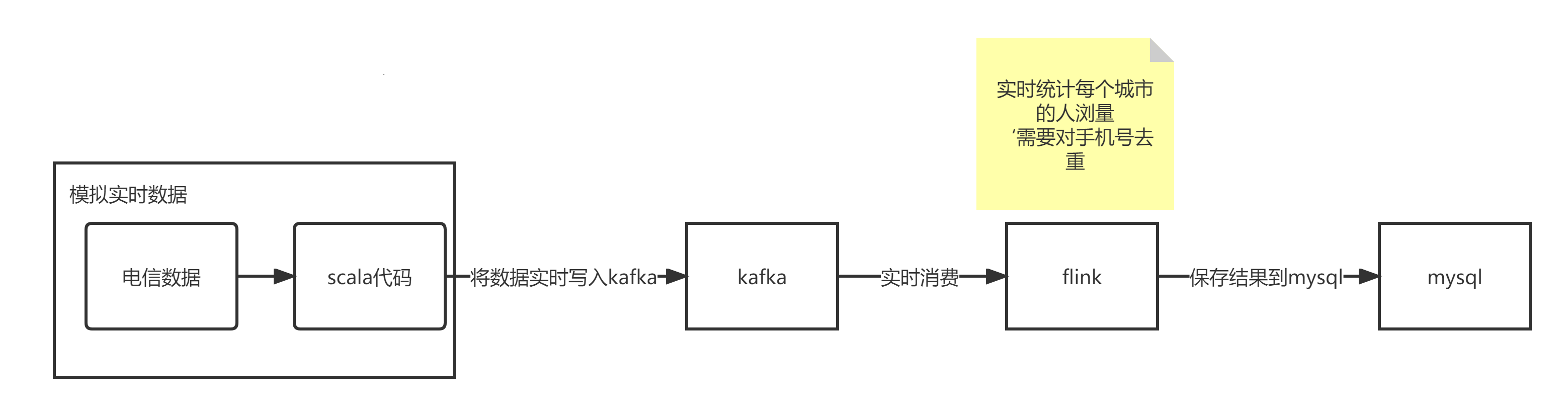
大数据之-kafka学习笔记
Kafka Kafka 是一个分布式的基于发布/订阅模式的消息队列(Message Queue),主要应用于大数据实时处理领域。 Kafka可以用作Flink应用程序的数据源。Flink可以轻松地从一个或多个Kafka主题中消费数据流。这意味着您可以使用Kafka来捕获和传输…...

虚幻动画系统概述
本文主要整理一下高层次的概述,方便后续查阅 1.动画流程 DCC产出动画文件 -> UE动画导入 -> 动画蓝图驱动(类似unity的动画状态机) ->动画后处理蓝图驱动(例如修型骨,骨骼矫正等后期处理) 2.动…...

什么是集成测试?集成测试方法有哪些?
1、基本概念: 将软件集成起来后进行测试。集成测试又叫子系统测试、组装测试、部件测试等。集成测试主要是针对软件高层设计进行测试,一般来说是以模块和子系统为单位进行测试。 2、集成测试包含的层次: 1. 模块内的集成,主要是…...

elementUI中的el-form常用校验规则
elementUI中的el-form常用校验规则: 校验使用方式: rules: {name: [{ required: true, message: 请输入活动名称, trigger: blur },{ min: 3, max: 5, message: 长度在 3 到 5 个字符, trigger: blur }],region: [{ required: true, message: 请选择活动区域, trig…...

蓝桥杯打卡Day9
文章目录 直角三角形最长平衡串 一、直角三角形IO链接 本题思路:本题就是利用欧几里得距离求解即可。 #include <bits/stdc.h>int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);int T;std::cin>>T;while(T--){int x…...
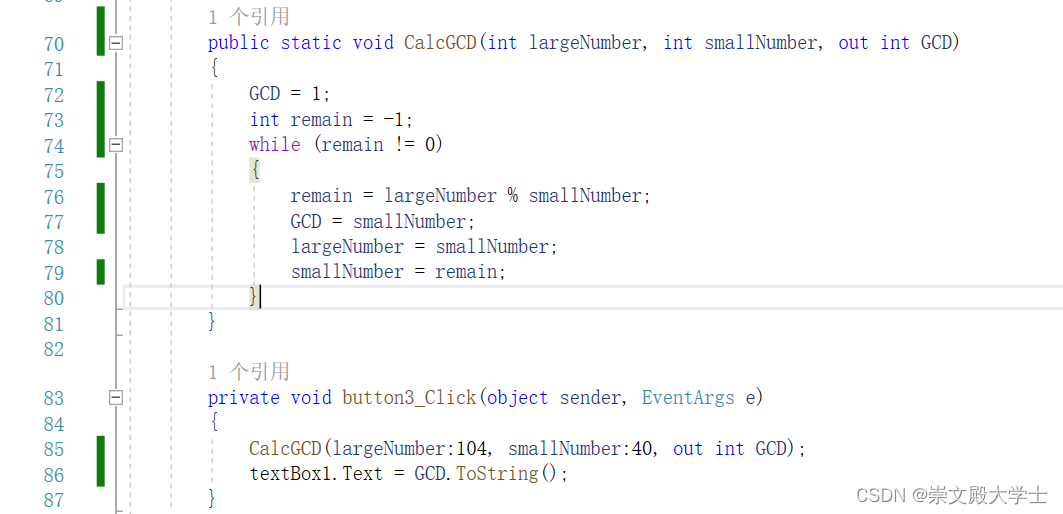
C# 辗转相除法求最大公约数
辗转相除法求最大公约数 public static void CalcGCD(int largeNumber, int smallNumber, out int GCD){GCD 1;int remain -1;while (remain ! 0){remain largeNumber % smallNumber;GCD smallNumber;largeNumber smallNumber;smallNumber remain;}}...
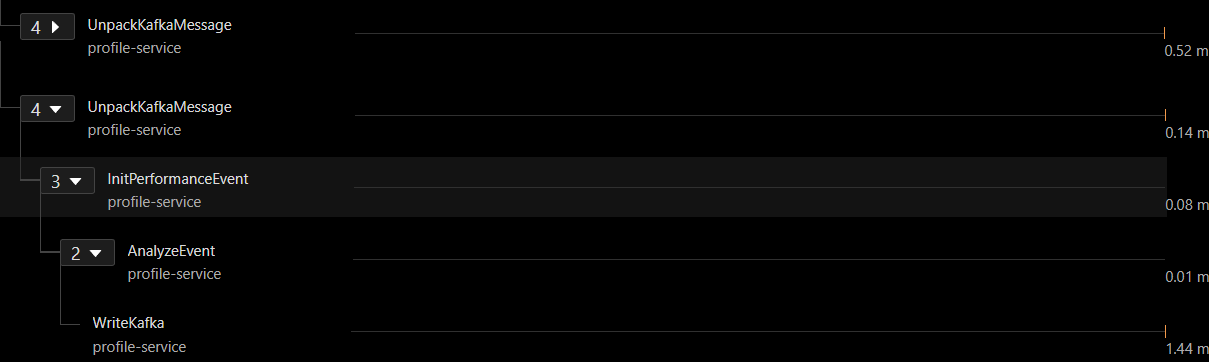
腾讯mini项目-【指标监控服务重构】2023-08-03
今日已办 a,b两组的trace放到一个分支里 可以看到先前的没看到的 profile trace 的耗时,是由于时间跨度较长,没有滑动到 trace 末尾 明日待办 组长会议汇报项目进度和问题...

redis缓存穿透、击穿、雪崩介绍
缓存穿透 概念 缓存穿透指某一特定时间批量请求打进来并访问了缓存和数据库都没有的key,此时会直接穿透缓存直达数据库,从而造成数据库瞬时压力倍增导致响应速度下降甚至崩溃的风险; 解决方案 一、通过布隆过滤器解决 原理:将…...

Redis 基础总结
1、NoSQL概述 1.1 数据库分类 目前数据库分:关系型数据库与非关系型数据库 常用的关系型数据库: Oracle,MySQL,SqlServer,DB2 常用的非关系数据库:Redis,MongoDB,ElasticSearch&…...
)
基于nginx的tomcat负载均衡和集群(超简单)
今天看到"基于apache的tomcat负载均衡和集群配置 "这篇文章成为javaEye热点。 略看了一下,感觉太复杂,要配置的东西太多,因此在这里写出一种更简洁的方法。 要集群tomcat主要是解决SESSION共享的问题,因此我利用memcac…...
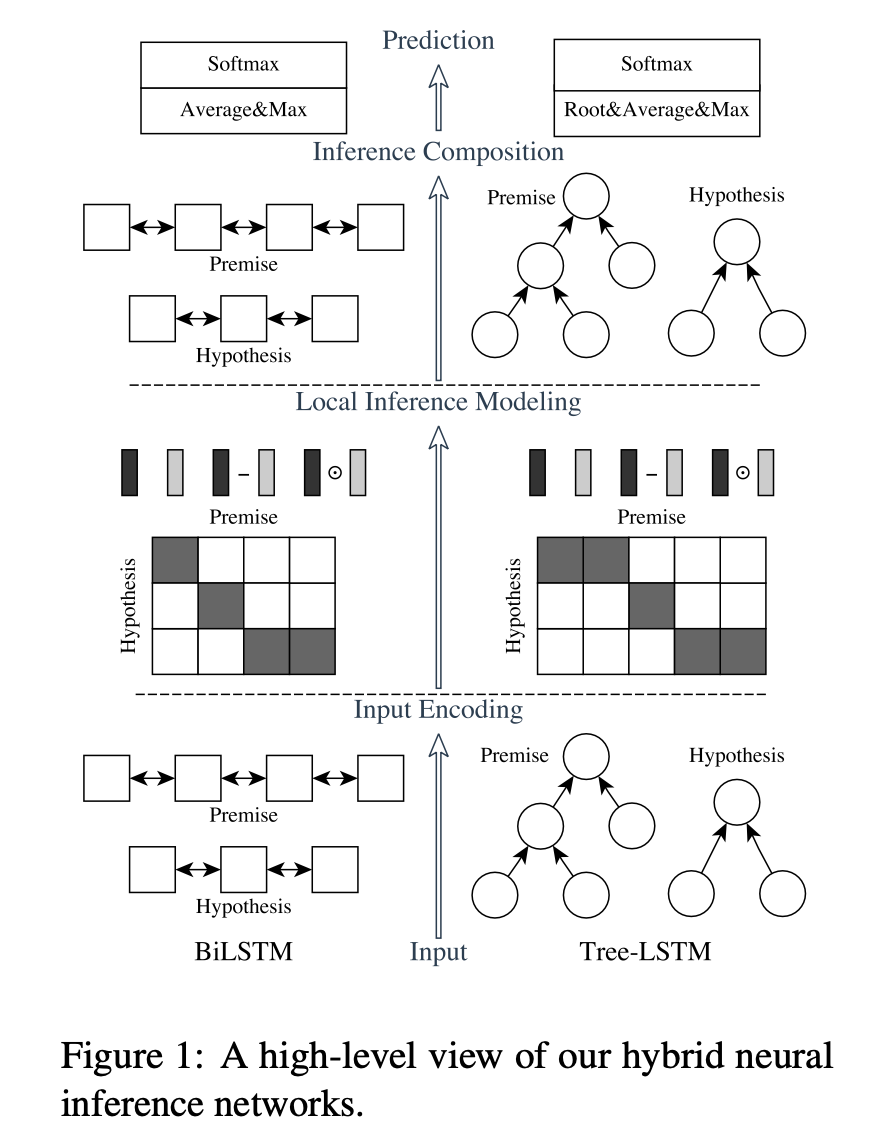
ESIM实战文本匹配
引言 今天我们来实现ESIM文本匹配,这是一个典型的交互型文本匹配方式,也是近期第一个测试集准确率超过80%的模型。 我们来看下是如何实现的。 模型架构 我们主要实现左边的ESIM网络。 从下往上看,分别是 输入编码层(Input Ecoding) 对前…...
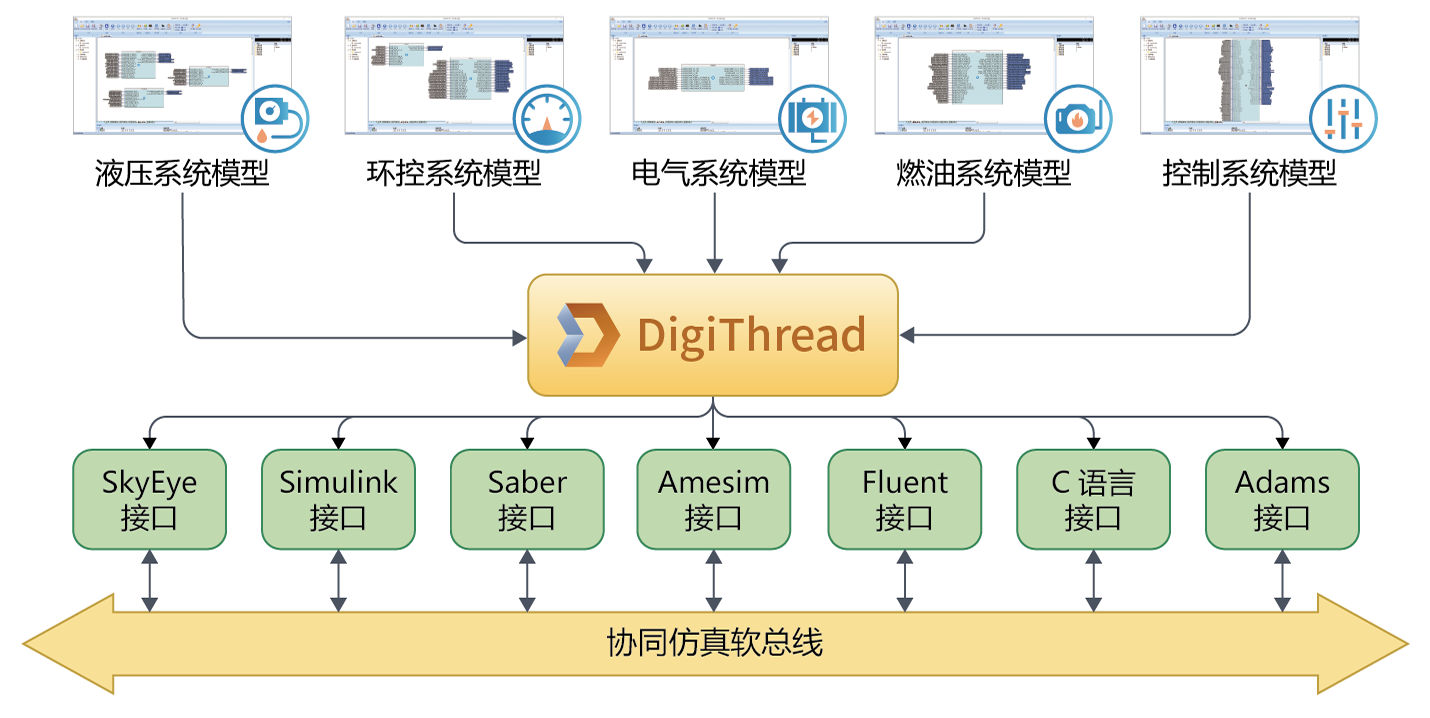
基于虚拟仿真技术的汽车燃油泵控制
在当前激烈的竞争环境下,汽车行业正在加速产业和技术更迭,整车厂对大型ECU嵌入式控制系统和软件的需求迫在眉睫。 然而,复杂而庞大的汽车系统往往由多个物理系统组成,系统所对应的模型都需要在不同的领域实现:发动机、…...

angular:HtmlElement的子节点有Shadow dom时奇怪的现象
描述: 这样写时,会自动跳过shadow dom节点的遍历 const cloneElement this.contentElement.cloneNode(true) as HTMLElement; for(let childNodeIndex 0; childNodeIndex < cloneElement.childNodes.length; childNodeIndex) {element.appendChild…...

栈与队列--删除字符串中的所有相邻重复项
给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。 在 S 上反复执行重复项删除操作,直到无法继续删除。 在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。 示例: 输入&#x…...
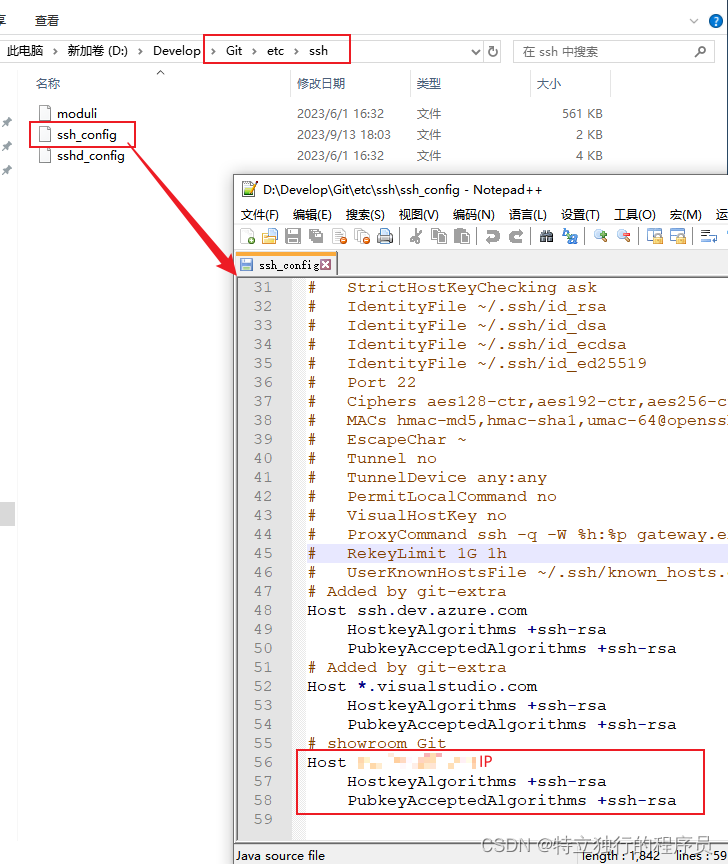
使用SSH地址拉取远程仓库代码报下面的错误
说明:配置了SSH秘钥后,使用SSH地址克隆代码,依旧无法拉取代码,提示下面这个信息。 Their offer:ssh-rsa,ssh-dss fatal:Could not read from remote repository. Please make sure you have the…...
easycms v5.5 分析 | Bugku S3 AWD排位赛
前言 这个awd打的悲,后台默认用户名密码为admin:admin,但是几乎所有人都改了 而且一进去看到这个cms就有点懵逼,都不知道这个cms是干嘛的(没用过相似的cms) 虽然网上找出了很多相关的漏洞,但是不知道为什…...
成都营运《乡村振兴战略下传统村落文化旅游设计》许少辉八一著作
成都营运《乡村振兴战略下传统村落文化旅游设计》许少辉八一著作...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

CSS 工具对比:UnoCSS vs Tailwind CSS,谁是你的菜?
在现代前端开发中,Utility-First (功能优先) CSS 框架已经成为主流。其中,Tailwind CSS 无疑是市场的领导者和标杆。然而,一个名为 UnoCSS 的新星正以其惊人的性能和极致的灵活性迅速崛起。 这篇文章将深入探讨这两款工具的核心理念、技术差…...

「Java基本语法」变量的使用
变量定义 变量是程序中存储数据的容器,用于保存可变的数据值。在Java中,变量必须先声明后使用,声明时需指定变量的数据类型和变量名。 语法 数据类型 变量名 [ 初始值]; 示例:声明与初始化 public class VariableDemo {publi…...
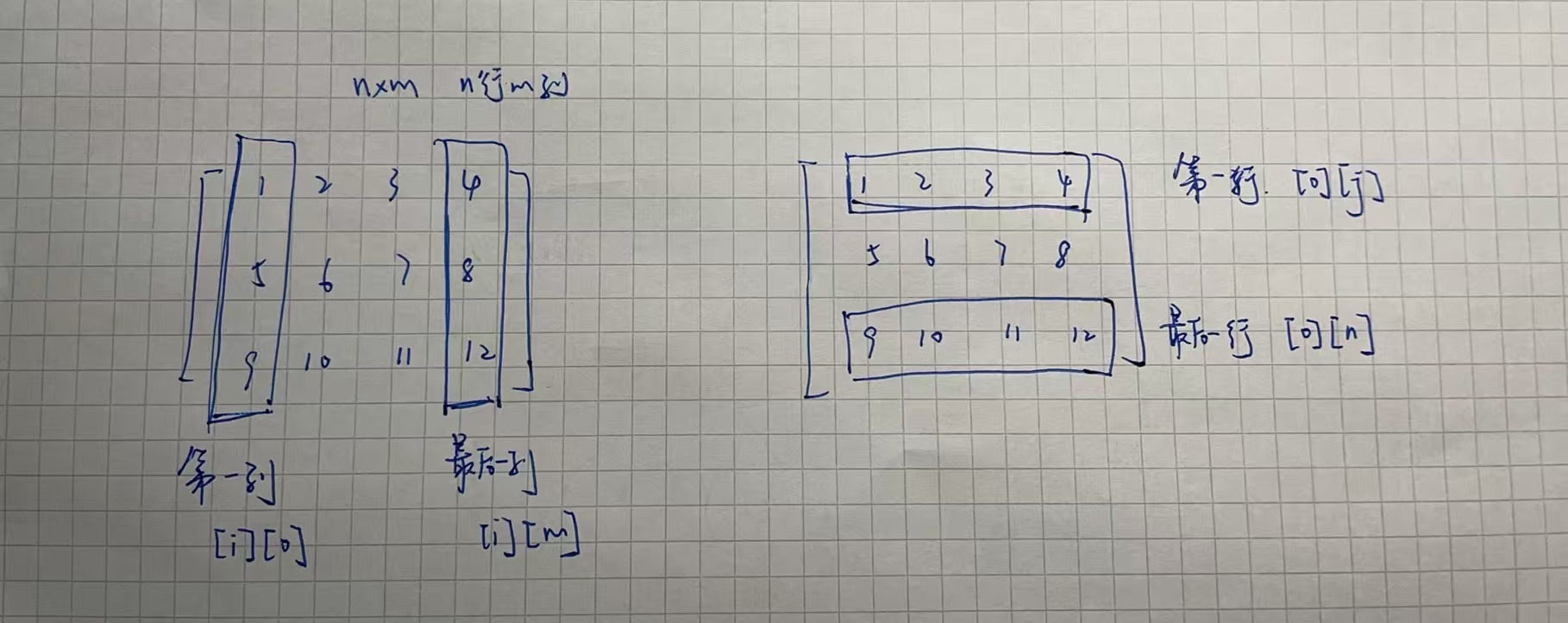
二维数组 行列混淆区分 js
二维数组定义 行 row:是“横着的一整行” 列 column:是“竖着的一整列” 在 JavaScript 里访问二维数组 grid[i][j] 表示 第i行第j列的元素 let grid [[1, 2, 3], // 第0行[4, 5, 6], // 第1行[7, 8, 9] // 第2行 ];// grid[i][j] 表示 第i行第j列的…...

STM32 低功耗设计全攻略:PWR 模块原理 + 睡眠 / 停止 / 待机模式实战(串口 + 红外 + RTC 应用全解析)
文章目录 PWRPWR(电源控制模块)核心功能 电源框图上电复位和掉电复位可编程电压监测器低功耗模式模式选择睡眠模式停止模式待机模式 修改主频一、准备工作二、修改主频的核心步骤:宏定义配置三、程序流程:时钟配置函数解析四、注意…...
