堆的概念和结构以及堆排序
前言
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结 构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
堆的概念及结构
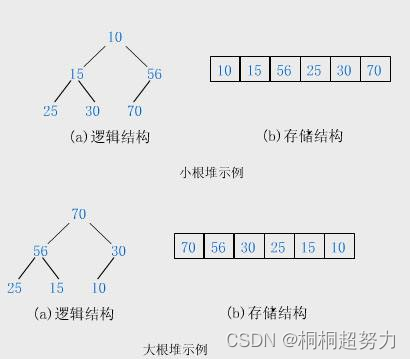
**堆(数据结构)**在逻辑上是一个完全二叉树而在物理上是一个数组。
堆是一种顺序存储结构(采用数组方式存储),仅仅是利用完全二叉树的顺序结构的特点进行分析。
已知二叉树根结点的下标是root,那么它左孩子的下标left=2*root+1,右孩子的下标right=2*root+2。
已知孩子结点的下标(不区分左右)为child,那么双亲的下标为(child-1)/2。
将满足根的值小于等于所有子树结点的值,称为小堆;根的值大于等于所有子树结点的值称为大堆。
堆的实现
我们实现堆还是要用三个文件,来让堆的代码看起来更加的简单易懂,
test.c,用来让测试堆的代码
Heap.c,我们些堆的函数
Heap.h,包括堆函数的头文件
(1)创建一个堆
这就是用一个结构体将这些内容,包括起来。
还是很简单的就不多介绍了
typedef int HPDatatype;
typedef struct Heap
{HPDatatype* a;int sz;int capacity;
}HP;
(2).堆的初始化
//堆的初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->sz = 0;php->capacity = 0;
}
(2)堆的销毁
我们用
malloc申请了空间,我们就要销毁。
//堆的销毁
void HeapDestory(HP* php)
{assert(php);free(php->a);php->a = NULL;php->sz = 0;php->capacity = 0;
}
(3).打印堆
//打印堆
void HeapPrint(HP* php)
{assert(php);for (int i = 0; i < php->sz; i++){printf("%d ", php->a[i]);}printf("\n");
}
(4)堆的添加元素
我们堆添加元素的思路,就是在数组的最后一位添加元素,然后看他的父节点是不是比他大或者小(创建大堆和创建小堆),如果是大堆,父节点比他小,就交换,然后知道最后交换到头结点。
这时我们就用到一种算法,叫做向上调整算法。
向上调整算法
//向上调整函数
void AdjustUp(HPDatatype* a,int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
交换函数
j进行数据的交换,因为后面用的会很多,就做成一个函数
//交换函数
void Swap(HPDatatype* p1,HPDatatype* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
添加堆元素的代码
//堆的添加元素
void HeapPush(HP* php, HPDatatype x)
{assert(php);//扩容if (php->sz == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDatatype* tmp = (HPDatatype*)realloc(php->a, sizeof(HPDatatype) * newcapacity);if (tmp == NULL){perror("realloc");exit(-1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->sz] = x;php->sz++;//向上调整函数AdjustUp(php->a,php->sz-1);
}
(5)删除堆顶的元素
我们堆删除元素,都是删除堆顶的元素,那么怎么删除元素了,
我们数组,最好删除的元素就是尾删,所以我们将第一个 元素和最后一个元素交换,然后我们sz--.
然后我们要保持他是一个堆,用到一个向下调整算法。
这个算法就是将最上面的元素,和他的最大的子节点进行交换,然后在进行到最后。
向下调整算法
void AdjustDown(HPDatatype* a, int n, int parent)
{//选大的子节点进行交换int child = parent * 2 + 1;while (child < n){//确认child指向大的孩子if (child + 1 < n && a[child + 1] < a[child]){child++;}//孩子大于父亲,就进行交换,继续向下调整//孩子小于父亲,则调整结束if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
删除元素的框架
//删除堆顶的数据,并保持他还是一个堆、
void HeapPop(HP* php)
{assert(php);assert(php->sz);//第一个和最后一个交换然后尾删Swap(&php->a[0], &php->a[php->sz - 1]);php->sz--;AdjustDown(php->a, php->sz, 0);
}
(6)找堆顶的元素
//找堆顶的元素
HPDatatype* HeapTop(HP* php)
{assert(php);assert(php->sz > 0);return php->a[0];
}
(7)查看堆的大小
//查看堆的大小
int HeapSize(HP* php)
{assert(php);return php->sz;
}
(8)判断堆是否为空
//判断堆是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->sz==0;
}
堆的构建
我们堆的构建用的算法是我们在删除元素的时候向下调整算法。
在排序之前,我们需要做一个准备工作,将数组放进去。看下面代码。
//堆的构建
void HeapCreate(HP* php, HPDatatype* a, int n)
{assert(php);//创建空间,将数组的的内容拷贝到我们的堆中,然后zaiphp->a = (HPDatatype*)malloc( sizeof(HPDatatype) * n);if (php->a == NULL){perror("realloc");exit(-1);}memcpy(php->a, a, sizeof(HPDatatype)*n);php->sz = php->capacity = n;}
经过上面的操作,我们将一个无序的数组放进去了,但是现在数组的内容并不是一个堆,现在我们用两种算法将这个数组变成堆。
向下调整的建堆算法
思路就是:我们想将最后一个叶子结点和他的父节点,先构成一个堆,然后我们再将父节点的上一个结点的子节点,将这个构建一个堆,知道最后到根结点。看下面我画的解释图。
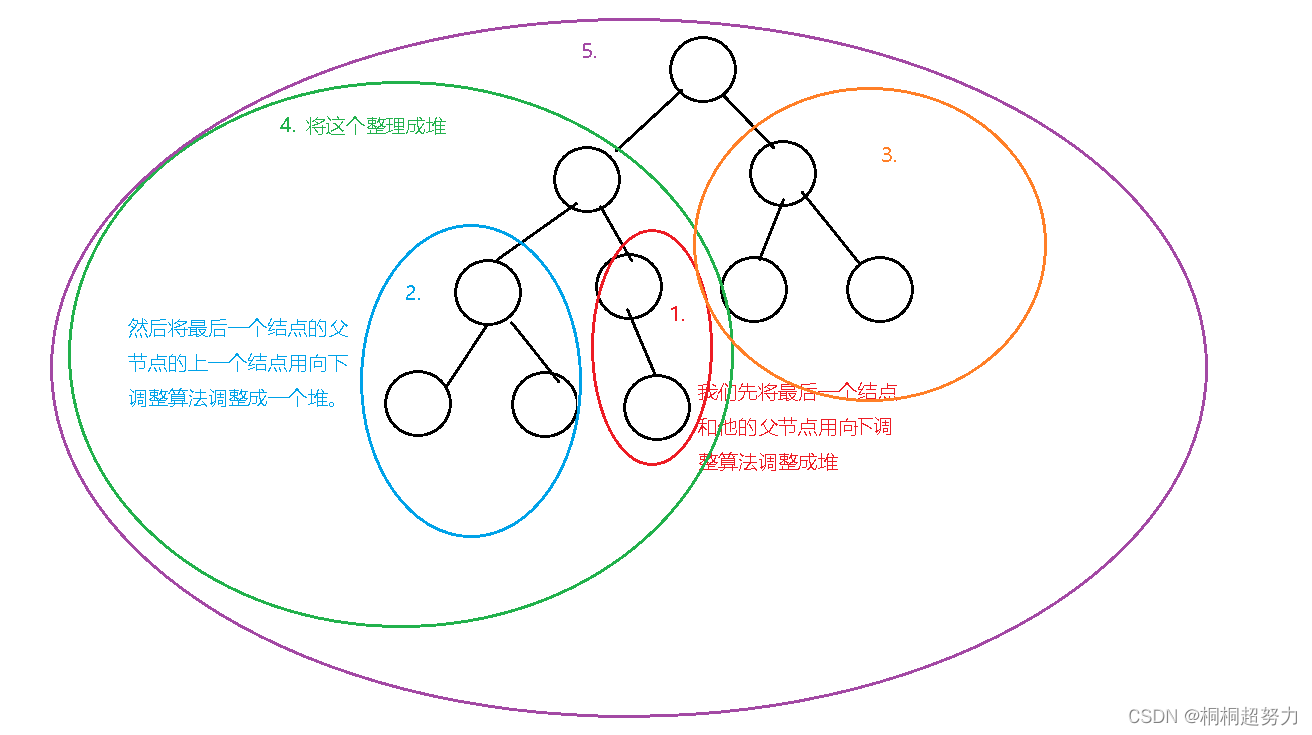
向下调整的建堆算法构建一个堆的代码
n表示这个数组有几个元素,而i表示我们的最后一个结点的父节点,然后就可以依次向下排序了,
//建堆算法for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(php->a, n, i);}
堆排序
我们想要堆排序,首先我们就要建堆,有了堆我们才可以排序,所以我们怎么将一个数组变成一个堆呢?
首先有两种方法,
1.第一种就是用插入的思想,将每一个数一个一个插进去,这时就要用我们的向上调整算法。
2.第二种方法就是用我们的上面用向下调整算法的思想建堆
向上调整算法建堆
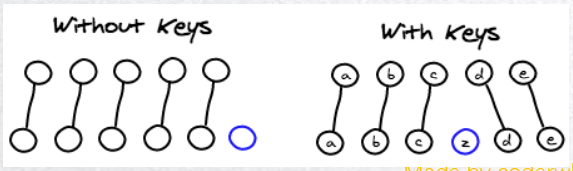
其实这个思想就是将我们的每一个数插入堆的方法,肯定大家又点不理解,下来画个图,大家就理解了
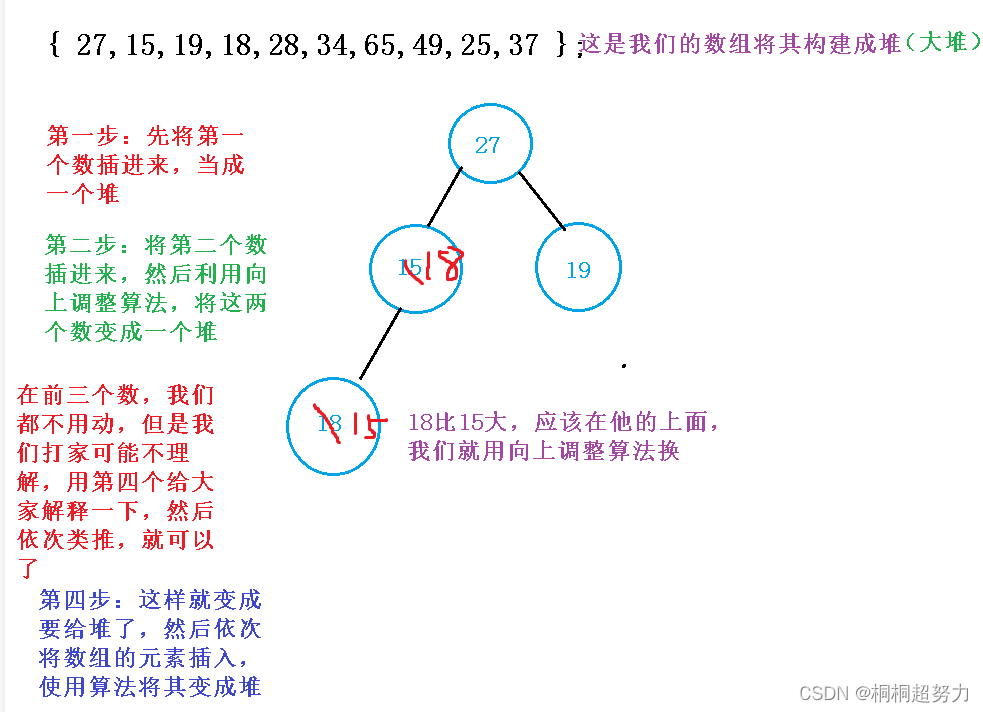
<1>向上调整算法建堆代码
就是如此的简单,将每个数遍历遍,依次使用建堆算法就ok了。
//向上调整建堆for (int i = 1; i < n; i++){AdjustUp(a, i);}
<2>向上调整建堆的时间复杂度
我们向上调整算法将每个数遍历一遍,然后将每个数的都要进行向上调整算法,我们就可以通过计算算,高度为h,
第一层不需要调整,
第二层开始调整,第二层有212^121个元素,每个再向上调整中进行了一次调整。
第三层有222^222,每个数最多调整2次
依次类推,在第n层,有2h−12^{h-1}2h−1个元素,每个元素换h-1次。
所以可以算出
f(h)=21∗1+22∗2+23∗3……2h−1∗(h−1)f(h)=2^1*1+2^2*2+2^3*3……2^{h-1}*(h-1)f(h)=21∗1+22∗2+23∗3……2h−1∗(h−1)
然后我们又知道N和h的关系,N=2h−1N=2^h-1N=2h−1
算所有的太复杂,所以我们直接算最后一个,因为最后一层的结点最多,而且调整次数最多,可以代表整个的时间复杂度将h换成N。
F(N)≈((N+1)(log2(N+1)−1))/2F(N)≈((N+1)(log_2(N+1)-1))/2F(N)≈((N+1)(log2(N+1)−1))/2
所以我们可以算出他的时间复杂对是O(N∗log2(N))O(N*log_2(N))O(N∗log2(N))
向下调整算法建堆
我们在堆的构建用的就是向下调整算法,思路和代码都讲了,但是我们为什们用向下调整算法,等我们算完下面的时间复杂度就知道。
<1>向下调整算法的时间复杂度
有的同学,看都不看,看到了两个循环,直接就说他的时间复杂度是O(N2N^2N2),这样都是打错特错了
首先分析一下,因为我们是从我们的最后一个数的父节点才开始算,我们的最后的叶子结点就不进行计算,而且我们想一下,我们的最多的结点不算,这种算法,一看这个时间复杂度就可以。
所以我们的最后一层没有进行堆排,
在我们的倒数第二层就进行一次调整
在倒数第三层进行2次调整
所以依次类推,第一层就进行h-1次调整
所以就可以计算
F(h)=2h−2∗1+2h−3∗2……22∗(h−2)+21∗(h−1)F(h)=2^{h-2}*1 + 2^{h-3}*2……2^2*(h-2)+2^1*(h-1)F(h)=2h−2∗1+2h−3∗2……22∗(h−2)+21∗(h−1)
所以我们可以看出这是一个等差数列*等比数列,用一个错位相减法我们就可以算出F(h)=2h−1−hF(h)=2^h-1-hF(h)=2h−1−h
我们又知道N=2h−1N=2^h-1N=2h−1,将h换成N就可以得到。
所以可以得出F(h)=N−log2(N+1)F(h)=N-log_2(N+1)F(h)=N−log2(N+1)
所以他的时间复杂度就是O(N).
比较两种算法
我们比较算法就是通过时间复杂度和空间复杂度进行比较,我们很容易就比较出来了,明显是向下调整算法好。他的时间复杂度底。
其实这个我们也可以通过画思路图就可以看明白了,
在向上调整算法中,我们的最后的结点最多,并且向上进行最多次,
而在向下调整算法中,我们最后一层的结点都不进行排序,并且在倒数第二层最多的结点才进行一次,而到了最高层最少的结点进行最多次。
如果我们要升序,建大堆还是建小堆
首先先说答案:建大堆。
思路:为什们建大堆,我们大堆的头就是最大的数,这是无容置疑的,然后我们将最大的数和堆最后一个数进行交换,我们的再用向下调整算法调整堆不包括最后一个最大的数,(利用我们堆的删除的思路)知道我们的堆就剩下一个。
for (int i = 0; i < n; i++){Swap(&a[0], &a[n - 1 - i]);AdjustDown(a, n - 1 -i, 0);}
这就是我们的堆排序
堆排序的时间复杂度
先说答案O(N∗log2(N))O(N*log_2(N))O(N∗log2(N))
可以类比一下,我们的向上调整算法,我们的最后一层是最多的一层,同时进行向下调整的次数也是最多的,所以我们直接算最后一层的就可以了,
而最后一层的个数是N=2h−1N=2^{h-1}N=2h−1,向下调整算法的时间复杂度为O(N)O(N)O(N),
最后看F(h)=2h−1∗(h−1)F(h)=2^{h-1}*(h-1)F(h)=2h−1∗(h−1)次然后进行换算一下,
O(N∗log2(N))O(N*log_2(N))O(N∗log2(N))
Top-K问题
- 什们是Top-K问题?
- 即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。 解决方法
-
- 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆,
前k个最小的元素,则建大堆
- 用数据集合中前K个元素来建堆
-
- 用剩余的N-K个元素依次与堆顶元素来比较,
不满足则替换堆顶元素将剩余N-K个元素依次与堆顶元素比完之后,
堆中剩余的K个元素就是所求的前K个最小或者最大的元素
- 用剩余的N-K个元素依次与堆顶元素来比较,
时间复杂度:K+(N−K)∗logkK+(N-K)*logkK+(N−K)∗logk=>O(N∗logk)O(N*logk)O(N∗logk)
空间复杂度:O(K)
相关文章:

堆的概念和结构以及堆排序
前言 普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结 构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事,…...
【Linux学习笔记】1.Linux 简介及安装
前言 本章介绍Linux及其安装方法。 Linux 简介 Linux 内核最初只是由芬兰人林纳斯托瓦兹(Linus Torvalds)在赫尔辛基大学上学时出于个人爱好而编写的。 Linux 是一套免费使用和自由传播的类 Unix 操作系统,是一个基于 POSIX 和 UNIX 的多…...

代码练习2~
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。def …...

微信小程序 之 云开发
一、概念1. 传统开发模式2. 新开发模式 ( 云开发模式 )3. 传统、云开发的模式对比4. 传统、云开发的项目流程对比5. 云开发的定位1. 个人的项目或者想法,不想开发服务器,直接使用云开发2. 某些公司的小程序项目是使用云开发的,但是不多&#…...

程序员的三门课,学习成长笔记
最近是有了解到一本好书,叫做程序员的三门课在这本书的内容当中我也确实汲取到了很多前辈能够传达出来的很多关于程序员职业规划以及成长路线上的见解,令我受益匪浅,故此想要把阅读完的每一章节结合自己的工作经验做一个精细化的小结…...

[技术经理]01 程序员最优的成长之路是什么?
00前言 谈起程序员的职业规划,针对大部分的职场人士,最优的成长之路应该是走技术管理路线,而不是走技术专家路线。 01关键的一步 中国自古就有“学而优则仕”的传统,发展到今天,在我们的现代企业里面,尤…...
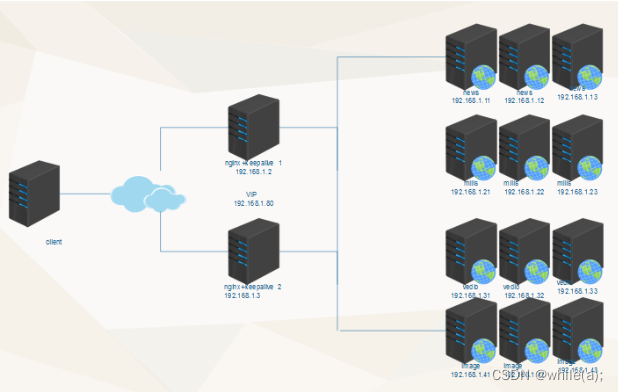
linux集群技术(三)--七层负载均衡-nginx
nginx特点nginx优势、缺点生产架构nginx 7层负载均衡语法示例nginx负载均衡算法测试案例生产案例 1.nginx特点 1. 功能强大,性能卓越,运行稳定。 2. 配置简单灵活。 3. 能够自动剔除工作不正常的后端服务器。 4. 上传文件使用异步模式。client---nginx---web1 web2 web3 lvs同…...
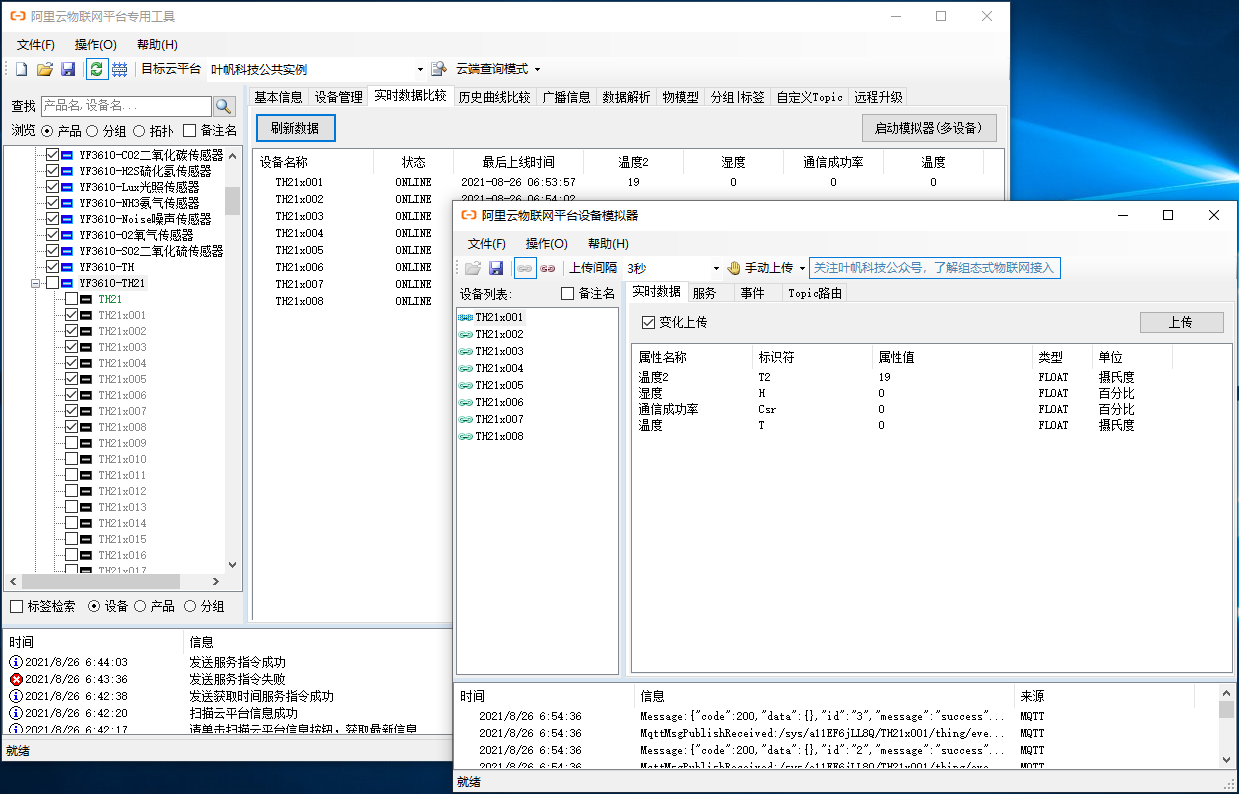
阿里云物联网平台设备模拟器
在使用阿里云物联网平台过程中,如果开始调试没有实际的物理设备,可以考虑在阿里云物联网平台使用官方自带的模拟器进行调试。不过也可以通过叶帆科技开发的阿里云物联网平台设备模拟器AliIoTSimulator进行调试,AliIoTSimulator可以独立运行&a…...
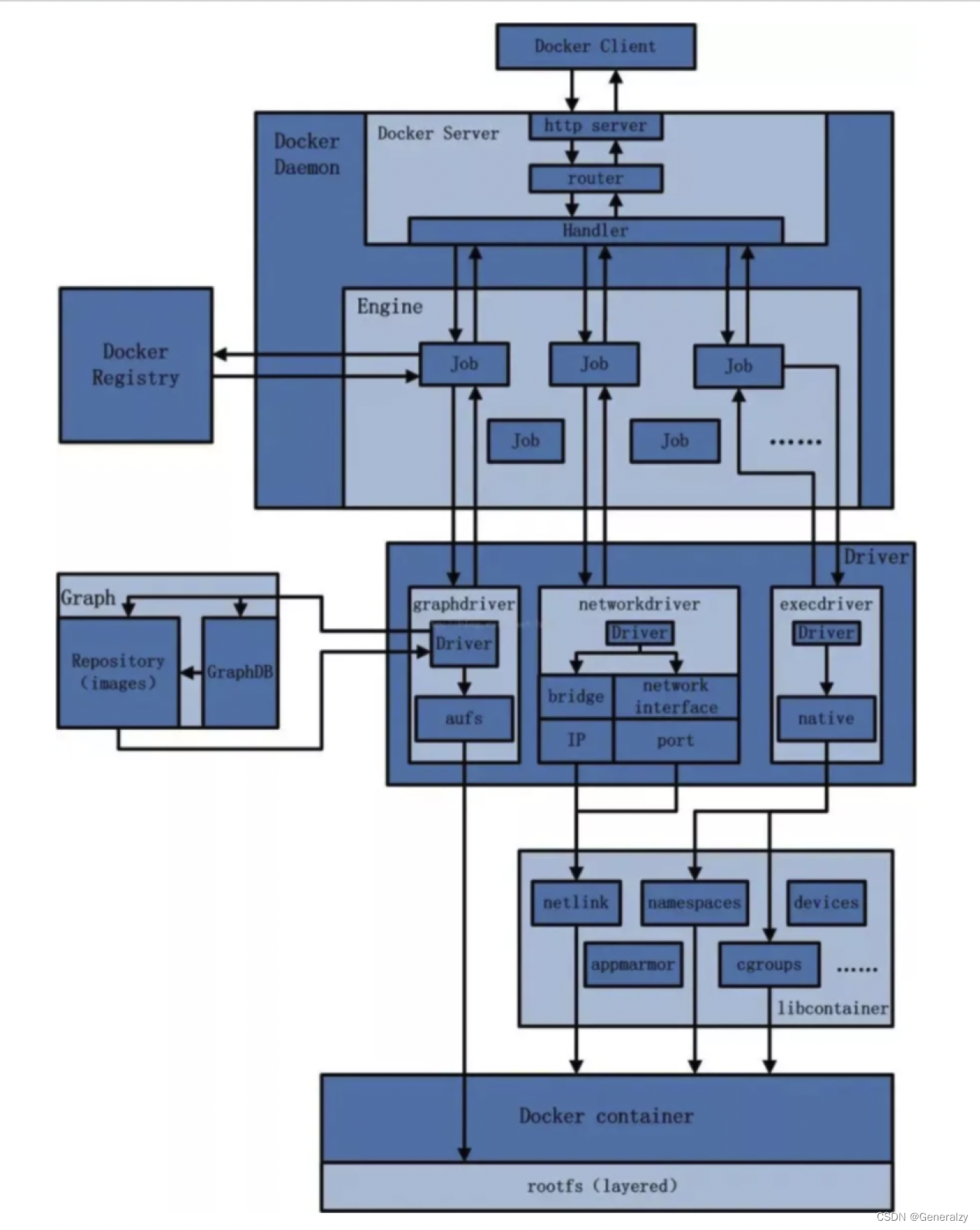
docker全解
目录说明docker简介为什么是docker容器与虚拟机比较容器发展简史传统虚拟机技术容器虚拟化技术docker能干什么带来技术职级的变化开发/运维(Devops)新一代开发工程师Docker应用场景why docker?docker的优势docker和dockerHub官网Docker安装CentOS Docker…...
Vue3 基础
Vue3 基础 概述 Vue (发音为 /vjuː/,类似 view) 是一款用于构建用户界面的 JavaScript 框架。它基于标准 HTML、CSS 和 JavaScript 构建,并提供了一套声明式的、组件化的编程模型,帮助你高效地开发用户界面。无论是简单还是复杂的界面&…...
【Linux】冯.诺依曼体系结构与操作系统
环境:centos7.6,腾讯云服务器Linux文章都放在了专栏:【Linux】欢迎支持订阅🌹冯.诺依曼体系结构什么是冯诺依曼体系结构?我们如今的计算机比如笔记本,或者是服务器,基本上都遵循冯诺依曼体系结构…...

WSO2 apim 多租户来区分api
WSO2 apim 多租户来区分api1. Tenant1.1 Add new tenant1.2 Add Role/User1.3 Published Api2. Delete Teant3. AwakeningWSO2安装使用的全过程详解: https://blog.csdn.net/weixin_43916074/article/details/127987099. Official Document: Managing Tenants. 1. Tenant 1.1 …...
)
TodoList(Vue前端经典项目)
TodoList主要是包含了CRUD功能,本地存储功能(loaclStorage)总结:全选按纽可以通过forEach循环来讲数据中的isCheck中的false删除实现就通过传递id,然后根据filter循环将符合条件的数据返回成数组,然后将返回…...

【扫盲】数字货币科普对于完全不了解啥叫比特币的小伙伴需要的聊天谈资
很多人并不清楚,我们时常听说的比特币,以太坊币,等等这些东西到底是一场骗局还是一场货币革命? 下面就围绕这数字货币的历史以及一些应用场景开始分析这个问题。 一、 开端 一切从2008年中本聪(Satoshi Nakamoto&…...

算法学习笔记:双指针
前言: 用于记录总结刷题过程中遇到的同类型问题 双指针问题及用法总结 1. 总结 双指针常用于遍历连序性对象(如数组、链表等)时,使用两个或多个指针进行单向遍历及相应的操作。避免多层循环,降低算法的时间复杂度。 …...

C++类的静态成员总结
tags: C OOP 引子: 类为什么需要静态成员 有时候类需要与它的一些成员与类本身直接相关, 而不是与类的各个对象都保持关联, 这就减少了成员与每一个类的实例对象的联系, 从而降低资源占用. 另一方面, 如果每次都需要重新更新该成员, 使得对象使用新的值, 这时候只需要修改一份…...

二、并发编程的三大特性
文章目录并发编程的三大特性1、原子性什么是并发编程的原子性?保证并发编程的原子性synchronizedCASLock锁ThreadLocal2、可见性什么是可见性?解决可见性的方式volatilesynchronizedLockfinal3、有序性什么是有序性?as-if-serialhappens-beforevolatile并发编程的…...

Ubuntu 22.04.2 LTS安装Apollo8.0
本人硬件环境: CPU:Intel Core i7 6700 显卡(GPU):NVIDIA GTX 3080 10G 内存:SAMSUNG DDR4 32GB 硬盘:双SSD系统盘 2T,双系统(windows,ubuntu) 一、安装Ubuntu 22.04…...

提高转化率的 3 个客户引导最佳实践
如果您的试用客户没有转化为付费客户,或者您总体上正在努力解决试用到付费转化率,那么您来对地方了。本文的最终目标是向您展示一些可用于提高自己的激活率和整体试用到付费转化的最佳客户引导实践。SaaS公司目前生活在一个以产品为主导的增长时代。换句…...

【消费战略】解读100个食品品牌丨元气森林 6年百亿的饮品黑马成功之道
元气森林成立于2016年,短短六年时间取得了近百亿营收的奇迹,成为让可口可乐、百事、娃哈哈、农夫山泉等消费巨头都无法忽视的对手。六年的成长堪比行业前辈20多年的积累,从这个角度而言,塔望咨询认为元气森林是成功的,…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
