什么是promise?
是JavaScript中用于处理异步操作的一种机制。
异步操作,例如从服务器获取数据、读取文件、执行数据库查询等等。
经典使用:Axios 是一个基于Promise的HTTP客户端
Promise具有三个状态:
-
Pending(待定):Promise的初始状态,表示操作尚未完成,仍在进行中。
-
Fulfilled(已完成):表示操作成功完成,并返回了一个值。一旦Promise达到这个状态,它就会保持不变,不会再改变状态。
-
Rejected(已拒绝):表示操作失败或出现错误,并返回了一个原因(错误信息)。一旦Promise达到这个状态,它也会保持不变,不会再改变状态。
Promise提供了以下方法和特性:
-
then(onFulfilled, onRejected): 用于添加处理成功和失败情况的回调函数。onFulfilled回调在Promise状态变为Fulfilled时执行,onRejected回调在状态变为Rejected时执行。这两个回调都接收Promise的结果或原因作为参数。 -
catch(onRejected): 用于捕获Promise的Rejected异常状态,相当于then(null, onRejected)。 -
finally(onFinally): 用于添加一个无论Promise状态如何都会执行的回调函数
// //修改权限请求updateUserStatus(authority, userId) {//开始发送修改请求var url = `http://localhost:8080/qy/User/UpdateUserStatus/${authority}/${userId}`;var config = {headers: {//配置请求表头防止后端接收不到data中的参数"Content-Type": "application/json",// 可以在这里添加其他的header配置},};this.axios.get(url, config).then((res) => {console.log("修改成功", res);}).catch((rej) => {//请求失败捕获console.log(rej);});},
相关文章:

什么是promise?
是JavaScript中用于处理异步操作的一种机制。 异步操作,例如从服务器获取数据、读取文件、执行数据库查询等等。 经典使用:Axios 是一个基于Promise的HTTP客户端 Promise具有三个状态: Pending(待定):Pr…...

从零开始学习软件测试-第45天笔记
monkey事件 事件:对app进行的操作,比如触摸事件,滑动事件...动作:构成一个事件所需要的步骤。 调整事件的百分比 adb shell monkey -p 包名 -v -v --pct-xxx 百分比 次数>输出文件的路径 分析日志有没有报错 到日志中去找…...

visual studio常用快捷键
CtrlM、CtrlO 折叠到定义 CtrlM、CtrlM 折叠当前定义 CtrlM、CtrlA 折叠全部 CtrlK、CtrlD 自动编排代码格式 F12 转到定义 ShiftF12 查看所有定义 ctrl] 转到定义首部或尾部 ctrlX 未选中文本时,剪切/删除光标所在行。ctrlV 未选中文本时,粘贴到…...

数据变换:数据挖掘的准备工作之一
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...

Go语言实践案例之简单字典
一、程序要实现效果: 在命令行调用程序的时候,可以在命令行的后面查询一个单词,然后会输出单词的音标和注释。 二、思路分析: 定义一个结构体 DictRequest,用于表示翻译请求的数据结构。其中包含了 TransType&#…...
)
笔试面试相关记录(3)
(1)String String和String.append()的底层实现 C中string append函数的使用与字符串拼接「建议收藏」-腾讯云开发者社区-腾讯云 (tencent.com) String String 在 第二个String中遇到\0就截止,append()的方法则是所有字符都会加在后面。 &…...
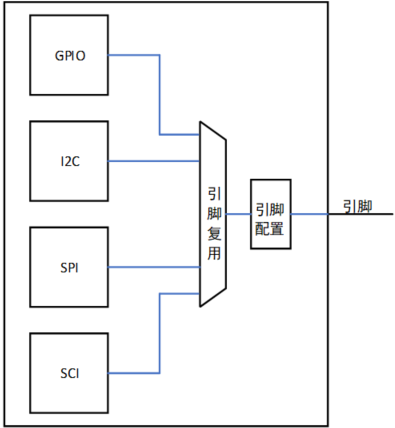
第6章_瑞萨MCU零基础入门系列教程之串行通信接口(SCI)
本教程基于韦东山百问网出的 DShanMCU-RA6M5开发板 进行编写,需要的同学可以在这里获取: https://item.taobao.com/item.htm?id728461040949 配套资料获取:https://renesas-docs.100ask.net 瑞萨MCU零基础入门系列教程汇总: ht…...

开源免费的流程图软件draw.io
2023年9月16日,周六上午 想买微软的visio,但发现不是很值得,因为我平时也不是经常需要画图。 所以我最后还是决定使用开源免费的draw.io来画图 draw.io网页版的网址: Flowchart Maker & Online Diagram Software draw.io的…...
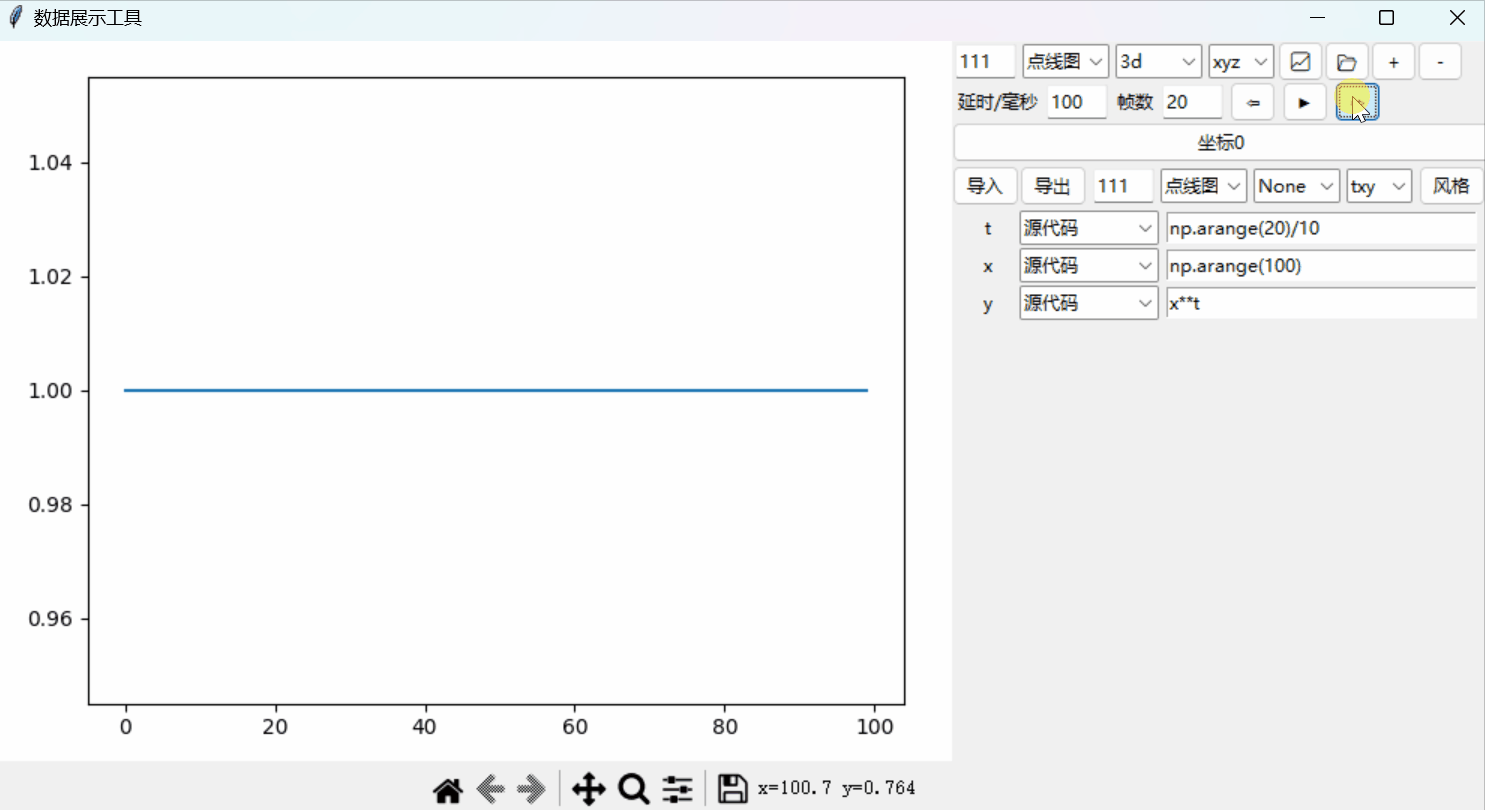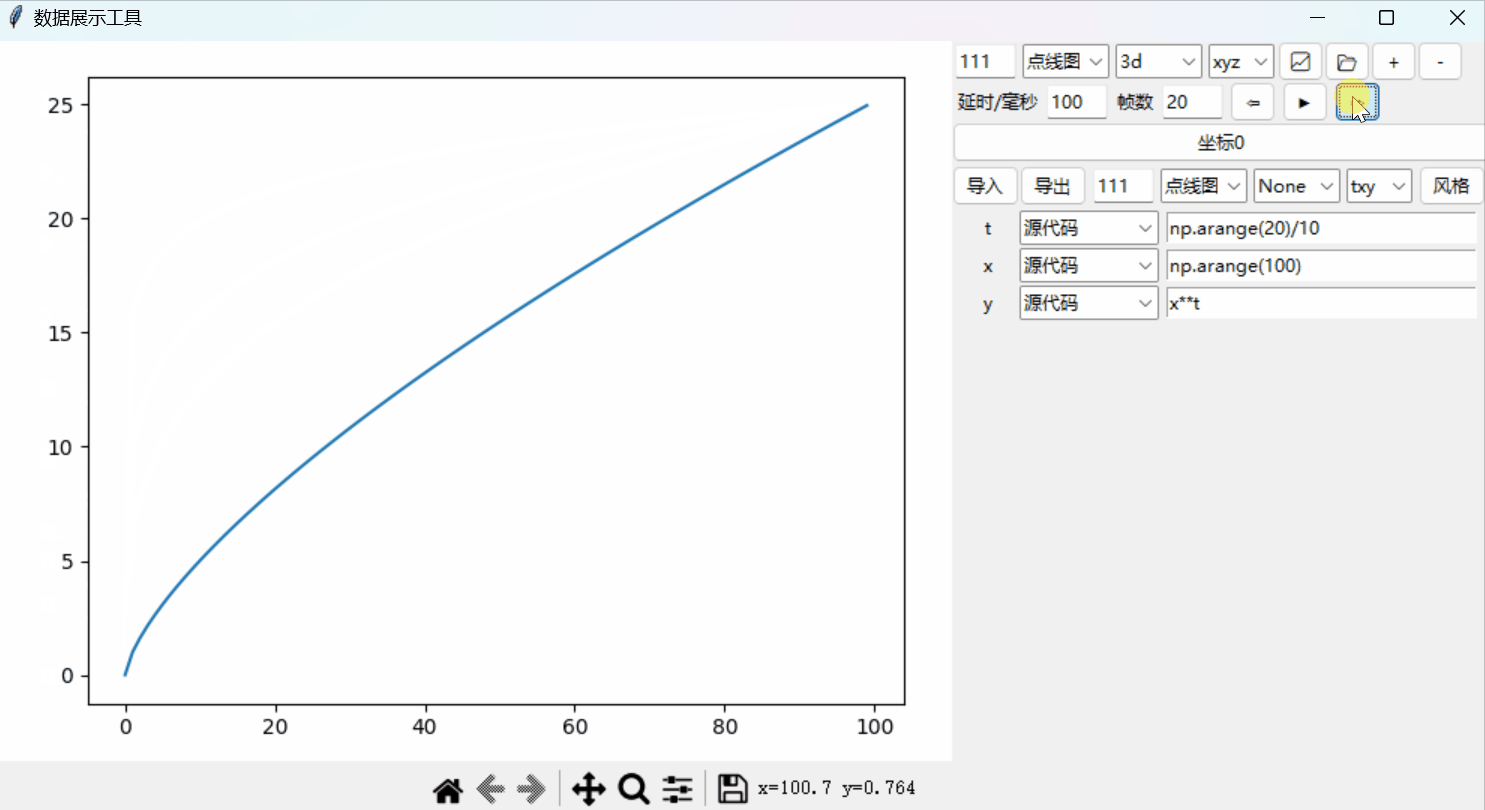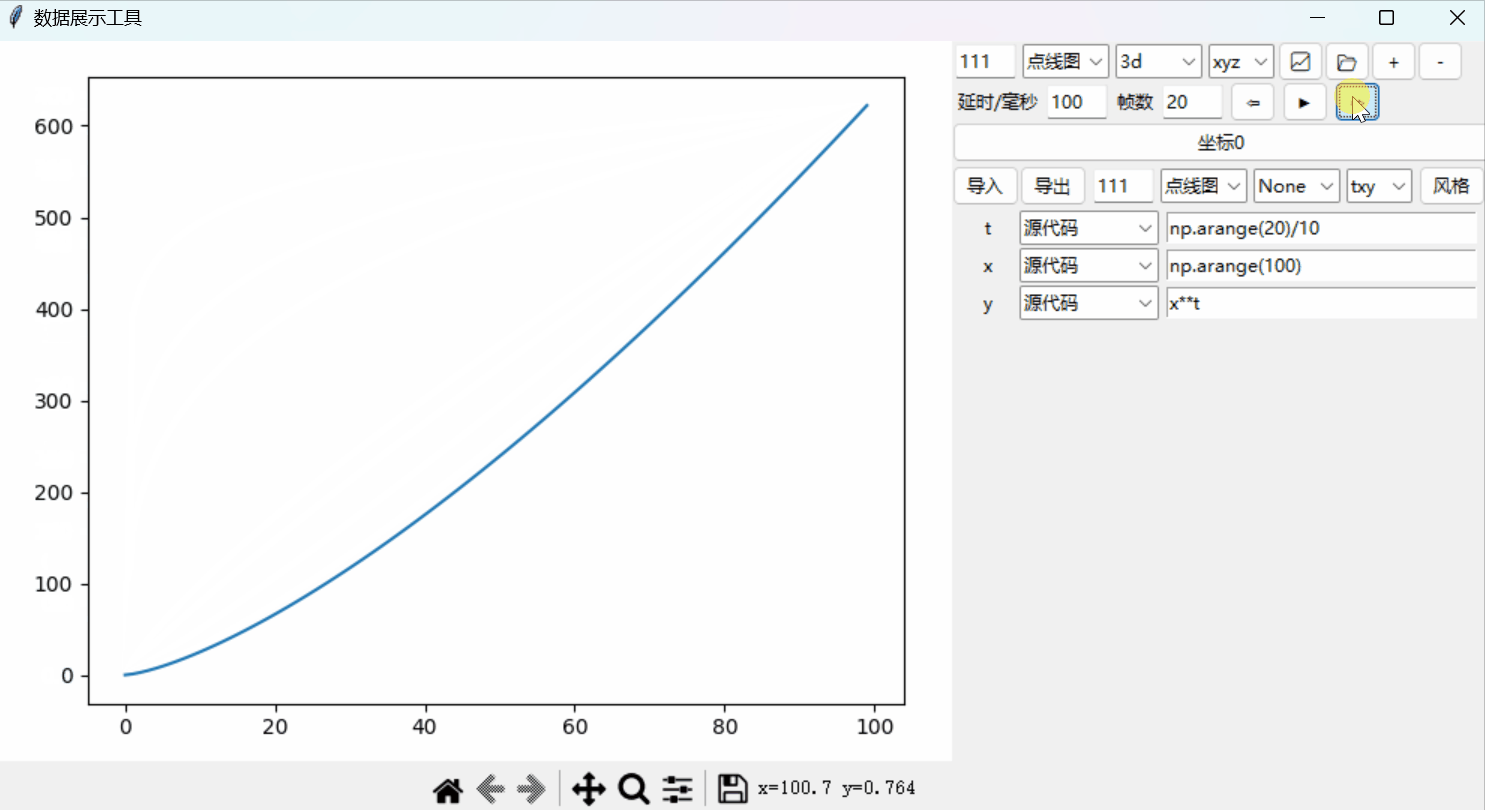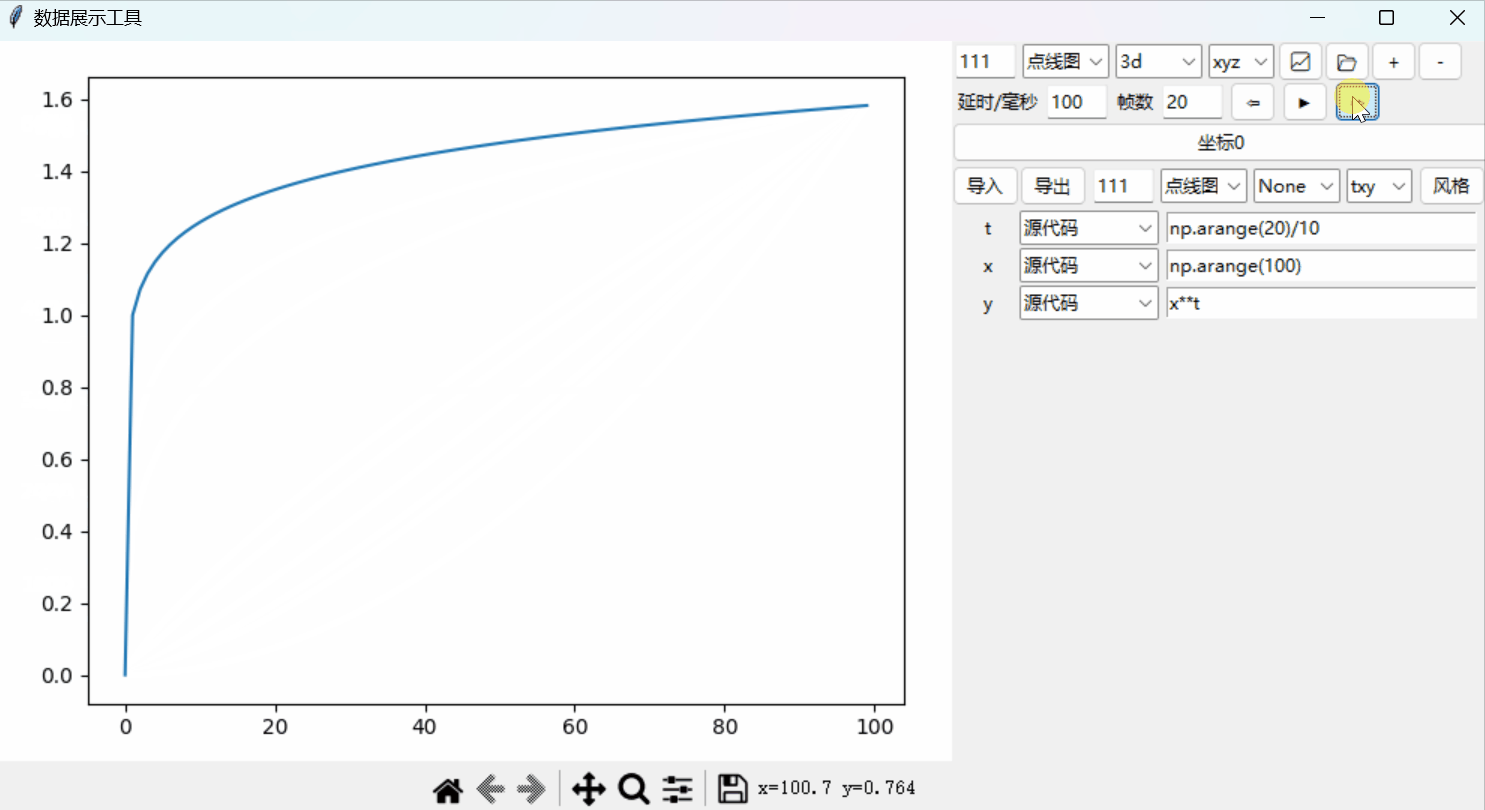
Python绘图系统19:添加时间轴以实现动态绘图
文章目录 时间轴单帧跳转源代码 Python绘图系统: 📈从0开始的3D绘图系统📉一套3D坐标,多个函数📊散点图、极坐标和子图自定义控件:绘图风格📉风格控件📊定制绘图风格坐标设置进阶&a…...
深度解析shell脚本的命令的原理之rm
rm 是 Unix/Linux 系统中的一个基本命令,用于删除文件或目录。以下是对这个命令的深度分析: 基本操作:rm 命令删除一个或多个文件或目录。这是通过从文件系统中移除链接来完成的。在 Unix/Linux 中,文件是通过链接(可以…...
)
RPA机器人流程自动化专题培训大纲(供大家参考使用)
一、RPA机器人流程自动化概述 RPA的定义和发展历程RPA的应用场景和优势RPA与人工智能的关系 二、RPA机器人流程自动化基础知识 RPA的基本原理和技术架构RPA的常用技术和工具RPA的编程语言和开发环境 三、RPA机器人流程自动化实战应用 如何进行业务流程分析与优化如何利用R…...
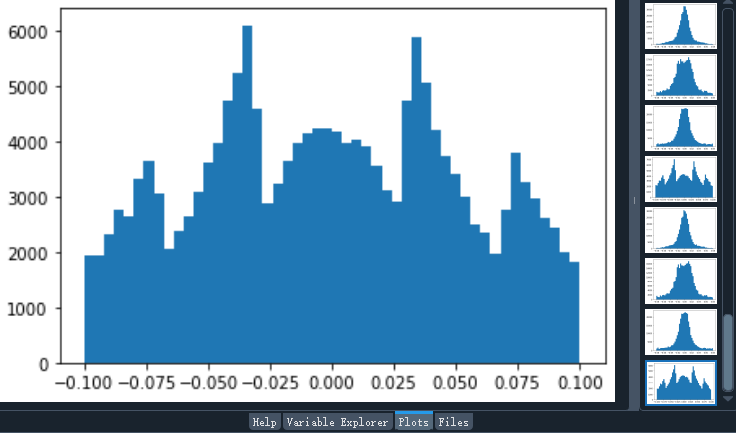
Python用若干列的数据多条件筛选、去除Excel数据并批量绘制直方图
本文介绍基于Python,读取Excel数据,以一列数据的值为标准,对这一列数据处于指定范围的所有行,再用其他几列数据数值,加以筛选与剔除;同时,对筛选与剔除前、后的数据分别绘制若干直方图ÿ…...
驱动开发,IO多路复用实现过程,epoll方式
1.框架图 被称为当前时代最好用的io多路复用方式; 核心操作:一棵树(红黑树)、一张表(内核链表)以及三个接口; 思想:(fd代表文件描述符) epoll要把检测的事件…...
java在mysql中查询内容无法塞入实体类中,报错 all elements are null
目录 一、问题描述二、解决方案 一、问题描述 java项目中整体配置了mysql的驼峰式字段匹配规则。 mybatis.configuration.map-underscore-to-camel-casetrue由于项目需求,需要返回字段为file_id,file_url,并且放入实体类中,实体…...
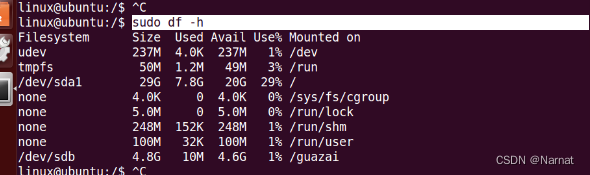
Linux 挂载
挂载需要挂载源和挂载点 虚拟机本身就有的挂源 添加硬件 重启虚拟机 操作程序 sudo fdisk -l //以管理员权限查看电脑硬盘使用情况sudo mkfs.ext4 /dev/sdb //以管理员身份格式化硬盘sudo mkdir guazai //创建挂载文件夹 sudo mount /dev/sdb/guazai //将挂载源接上挂载点 s…...

[面试] 15道最典型的k8s面试题
文章目录 在 Kubernetes 中,有以下常见的资源对象:1.什么是 Kubernetes?它的主要特点是什么?2. Kubernetes 中的 Pod 是什么?它的作用是什么?3.Kubernetes 中的 Deployment 和 StatefulSet 有何区别&#x…...

lintcode 552 · 创建最大数 【算法 数组 贪心 hard】
题目 https://www.lintcode.com/problem/552/description 描述 给出两个长度分别是m和n的数组来表示两个大整数,数组的每个元素都是数字0-9。从这两个数组当中选出k个数字来创建一个最大数,其中k满足k < m n。选出来的数字在创建的最大数里面的位置…...
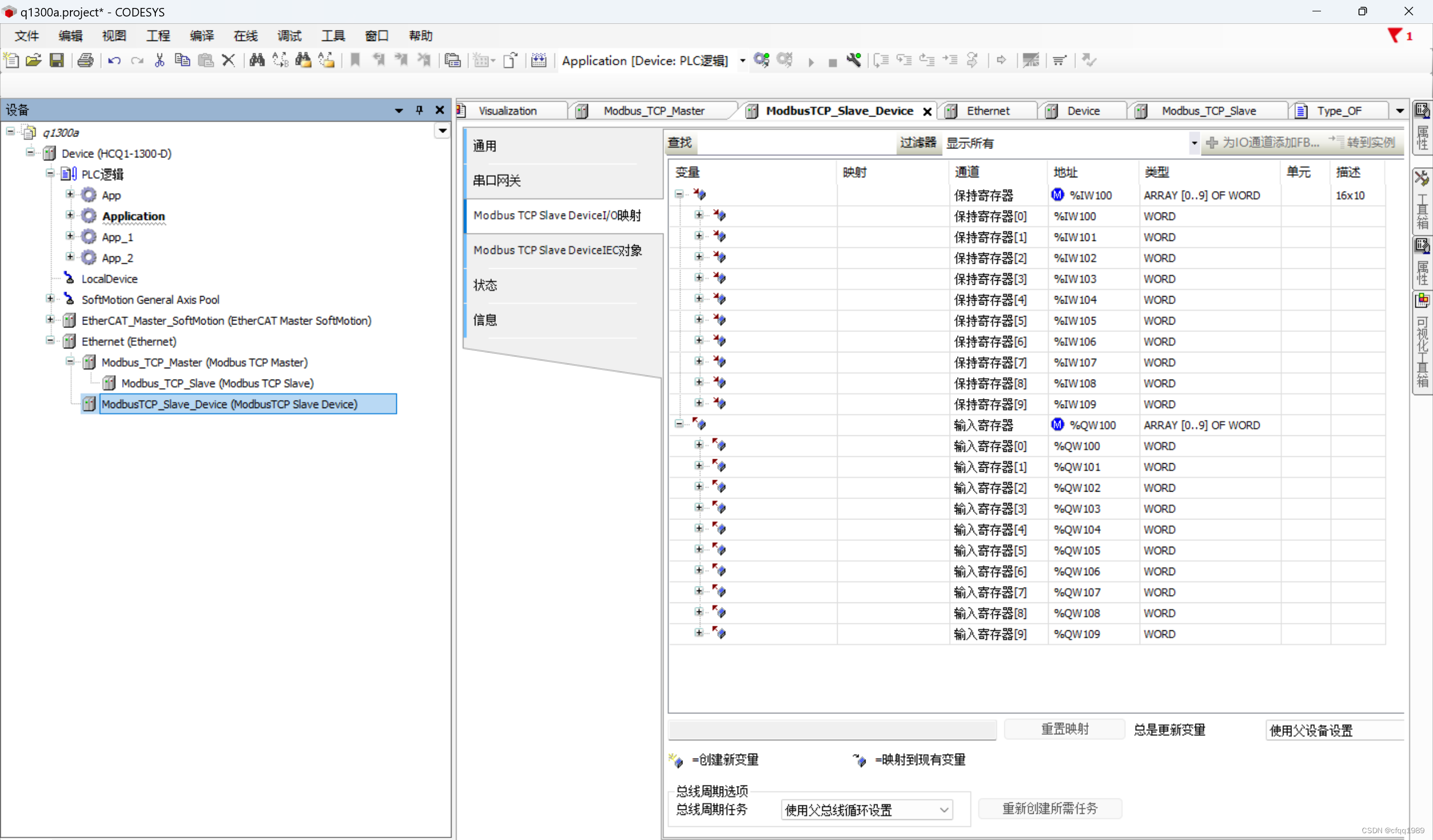
ModbusTCP服务端
1在Device下,添加设备net: 公交车。 2在net下添加 ModbusTCP...

Middleware ❀ Hadoop功能与使用详解(HDFS+YARN)
文章目录 1、服务概述1.1 HDFS1.1.1 架构解析1.1.1.1 Block 数据块1.1.1.2 NameNode 名称节点1.1.1.3 Secondary NameNode 第二名称节点1.1.1.4 DataNode 数据节点1.1.1.5 Block Caching 块缓存1.1.1.6 HDFS Federation 联邦1.1.1.7 Rack Awareness 机架感知 1.1.2 读写操作与可…...
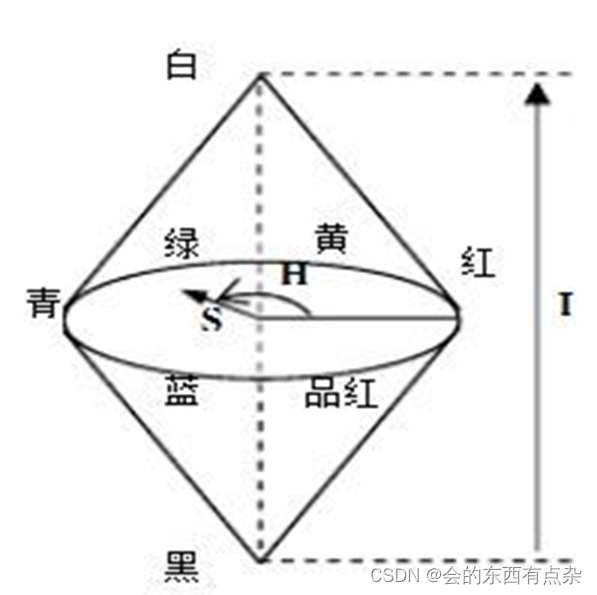
Matlab图像处理-从RGB转换为HSV
从RGB转换为HSV HSV彩色系统基于圆柱坐标系。从RGB转换为HSV需要开发将(笛卡儿坐标系中的)RGB值映射到圆柱坐标系的公式。多数计算机图形学教材中已详细推导了这一公式,故此处从略。 从RGB转换为HSV的MATLAB函数是rgb2hsv,其语法为: hsv_imag…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
