数据结构——图(图的存储及基本操作)
文章目录
- 前言
- 一、邻接矩阵法(顺序存储)
- 1.无向图存储邻接矩阵算法
- 2.有向图存储邻接矩阵算法
- 二、邻接表法(图的链式存储结构)
- 总结
前言
- 邻接矩阵法(图的顺序存储结构)
1.1 无向图邻接矩阵算法
1.2 有向图邻接矩阵算法 - 邻接表法(图的一种链式存储结构)
一、邻接矩阵法(顺序存储)
- 定义:用一个一维数组存储顶点,一个二维数组存储边的信息(各顶点之间邻接关系),n个顶点是n×n的矩阵,若(vi,vj)属于E ,则A[i][j]=1,否则等于0;对于带权图,则邻接矩阵中对应项存放着该边对应的权值,若顶点vi和vj不相连,则用∞来表示这两个顶点之间不存在边【是表示顶点之间相邻关系的矩阵。所谓两顶点的相邻关系即它们之间有边相连。】
- 注意
①无向图的邻接矩阵是对称矩阵,对规模特大的邻接矩阵可采用压缩存储
②邻接矩阵表示法的空间复杂的为O(n^2),其中n为图的定点数|V| - 图的邻接矩阵存储表示法具有以下特点:
1)无向图的邻接矩阵一定是一个对称矩阵(并且唯一),因此,在实际存储邻接矩阵时只需存储上(或下)三角矩阵的元素即可
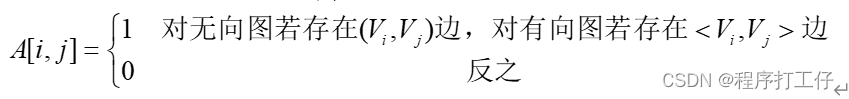
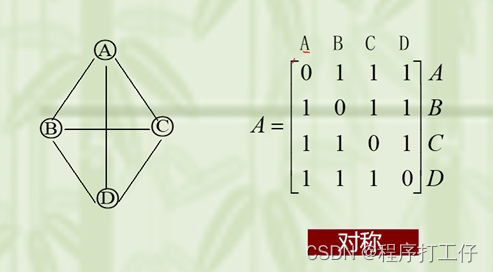
2)对于无向图,邻接矩阵的第i行(或第i列)非零元素(或非无穷元素)的个数正好是第i个顶点的度TD(vi)
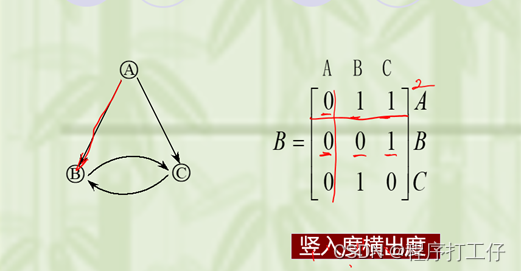
3)对于有向图,邻接矩阵的第i行(或第i列)非零元素(或非无穷元素)的个数正好是第i个顶点的出度OD(vi)(或入度ID(vi)),第i行和第i列和是有向图第i结点的度
(有向图:行出度,竖入度)
4)用邻接矩阵存储图,很容易确定图中任意两个顶点时间是否有边相连。但是,要确定图中有多少边,则必须按行、按列对每个元素进行检测,所花费的时间代价很大。这是用邻接矩阵存储图的局限性
5)稠密图适合使用邻接矩阵的存储表示
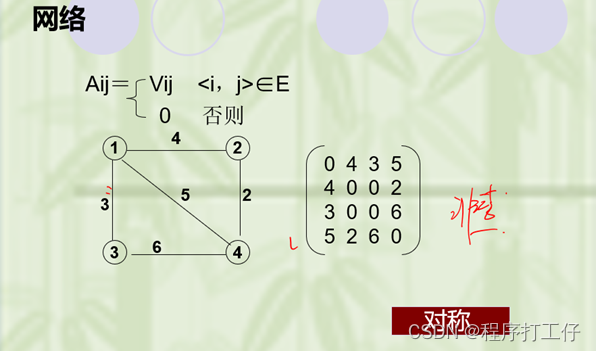
- 无向图的邻接矩阵是对称的,如果A[i,j]=1,必有A[j,i]=1。这说明,只输入和存储其上三角阵元素即可得到整个邻接矩阵。
- 一般有向图的邻接矩阵是不对称的,A[i,j]不一定等于A[j,i]。
- 邻接矩阵用二维数组即可存储,定义如下:
int adjmatrix = ARRAY[n][n]; - 如果图的各边是带权的,只需将矩阵中的各个1元素换成相应边的权即可。
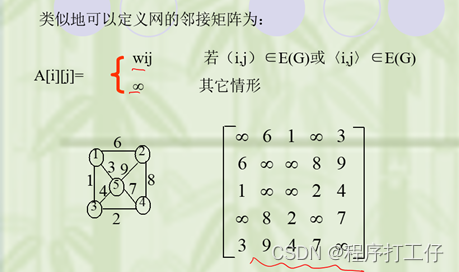
- 对于无向图而言:顶点Vi的度是邻接矩阵中第i行(或列)的元素之和。
- 对于有向图而言:
顶点Vi的出度是邻接矩阵中第i行的元素之和。
顶点Vi的入度是邻接矩阵中第i列的元素之和
1.无向图存储邻接矩阵算法
int creatgraph (int adjarray[ ][ ])
{int i,j,v1,v2,num;scanf (“%d”,&num); /*输入顶点数*/if (num>0){for (i=1;i<=num;i++)for (j=1;j<=num;j++)adjarry [i][j]=0; /*矩阵初始化*/
do{scanf (“%d,%d”,&v1,&v2); /*输入边*/adjarray[v1][v2]=1;adjarray[v2][v1]=1;} while(v1!=0 && v2!=0);}else num=0;return num;}2.有向图存储邻接矩阵算法
int creatgraph (int adjarray[ ][ ])
{int i,j,v1,v2,num;scanf (“%d”,&num); /*输入顶点数*/if (num>0){for (i=1;i<=num;i++)for (j=1;j<=num;j++)adjarry [i][j]=0; /*矩阵初始化*/
do{scanf (“%d,%d”,&v1,&v2); /*输入边*/adjarray[v1][v2]=1;} while(v1!=0 && v2!=0);}else num=0;return num;}二、邻接表法(图的链式存储结构)
1.定义:对图G中每个顶点建立一个单链表,第i个单链表结点表示依附于顶点vi的边(有向图是以顶点vi为尾的弧)
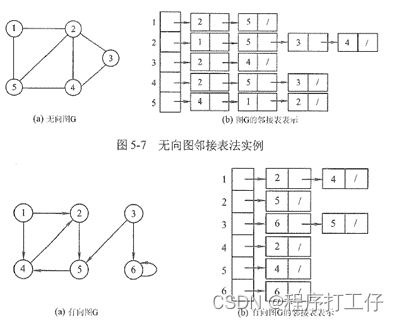
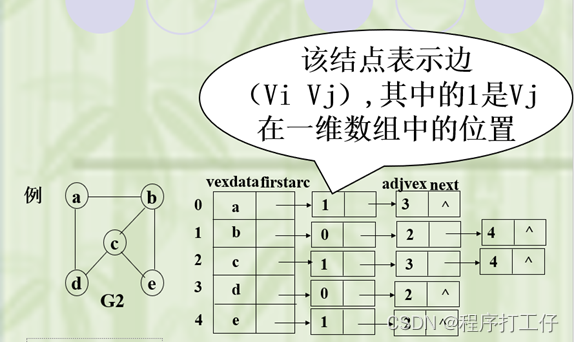
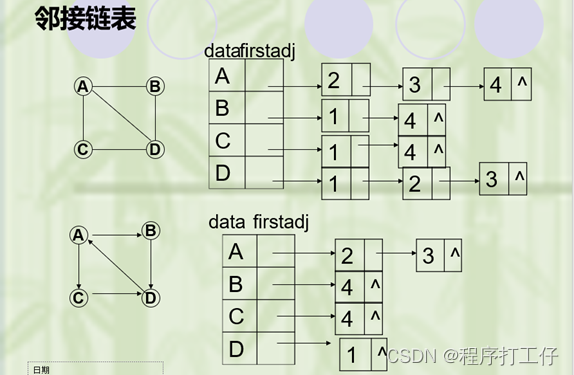
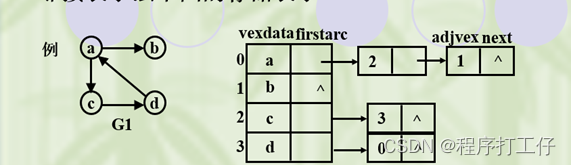
2. 邻接表特点
(1)如果G为无向图,则所需存数空间为O(|V|+2|E|),若为有向图,则需O(|V+|E|)
(2)邻接表中给定一顶点,能够很容易找到所有邻边,而邻接矩阵中需要扫描一行,时间为O(n);但是若要确定两个顶点间是否存在边,则在邻接矩阵里可以立即查找,而在邻接表需要对相应结点的边表里查找另一结点,效率较低
(3)有向图邻接表中,求一个给定顶点的出度只需计算其邻接表结点个数,但要求入度,需遍历整表,也可用逆邻接表
(4)无向图设存储顶点的一维数组大小为m(m>=图的顶点数n),
图的边数为e,G占用存储空间为:m+2*e。(有向图)G占用存储空间与G的顶点数、边数均有关;适用于边稀疏的图
(5)有向图中
顶点Vi的出度为第i个单链表中的结点个数
顶点Vi的入度为整个单链表中邻接点域值是i的结点个数
判定两顶点v,u是否邻接:要看v对应线性链表中有无对应的结点u
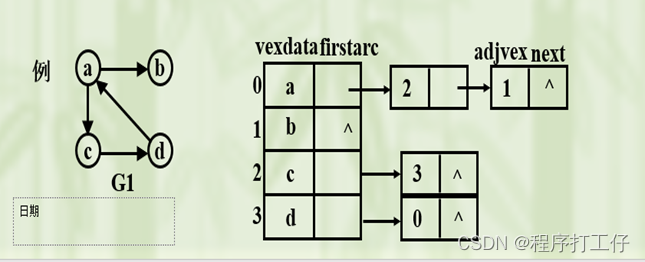
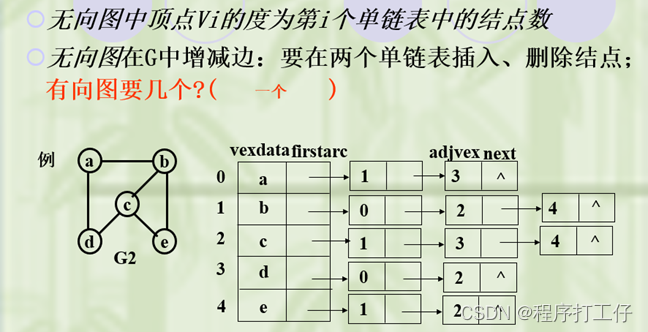
总结
- 邻接矩阵法(图的顺序存储结构)
1.1 无向图邻接矩阵算法
1.2 有向图邻接矩阵算法 - 邻接表法(图的一种链式存储结构)
相关文章:

数据结构——图(图的存储及基本操作)
文章目录 前言一、邻接矩阵法(顺序存储)1.无向图存储邻接矩阵算法2.有向图存储邻接矩阵算法 二、邻接表法(图的链式存储结构)总结 前言 邻接矩阵法(图的顺序存储结构) 1.1 无向图邻接矩阵算法 1.2 有向图邻接矩阵算法邻接表法(图的一种链式存储结构) 一…...

2023年项目管理工具使用趋势分析及预测
随着技术的不断进步以及工作和领导态度的演变,各个行业都在经历着深刻的变革。项目管理领域同样如此,团队项目的技术和人员管理风格及策略正在不断地调整与优化,以适应新冠疫情后所呈现出的新的工作场所格局。在此背景下,以下是我…...
)
Vue3 实现一个无缝滚动组件(支持鼠标手动滚动)
Vue3 实现一个无缝滚动组件(支持鼠标手动滚动) 前言 在日常开发中,经常遇到需要支持列表循环滚动展示,特别是在数据化大屏开发中,无缝滚动使用频率更为频繁,在jquery时代,我们常用的无缝滚动组…...
【IP数据报】IP地址和MAC地址的区别
1、用IP地址来标识Internet的主机 在每个IP数据报中,都会携带源IP地址和目标IP地址来标识该IP数据报的源和目的主机。IP数据报在传输过程中,每个中间节点(IP 网关)还需要为其选择从源主机到目的主机的合适的转发路径(即路由)。IP协议可以根据路由选择协…...

高并发笔记
如何设计一个高并发系统?:https://mp.weixin.qq.com/s/yFc-70DEhloWn0G3GDa6Yw 分布式 ID 服务实践:https://mp.weixin.qq.com/s/KAts9Zjj8JpEd0Q6pqLlgQ 一文聊透布隆过滤器:https://mp.weixin.qq.com/s/qJ2fDm1Z57bPSzOBrgiqfg …...
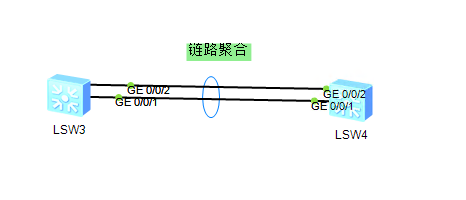
eNSP网络学习
一、eNSP 1.什么是eNSP eNSP(Enterprise Network Simulation Platform)是一款由华为提供的免费的、可扩展的、图形化操作的网络仿真工具平台,主要对企业网络路由器、交换机进行软件仿真,完美呈现真实设备实景,支持大型网络模拟,让…...
广州xx策划公司MongoDB恢复-2023.09.09
2023.09.08用户的MongoDB数据库被勒索病毒攻击,数据全部被清空。 提示: mongoDB的默认端口为27017,黑客通常通过全网段扫描27017是否开放判断是否是MongoDB服务器。一旦发现27017开放,黑客就会用空密码、弱密码尝试连接数据库。黑…...
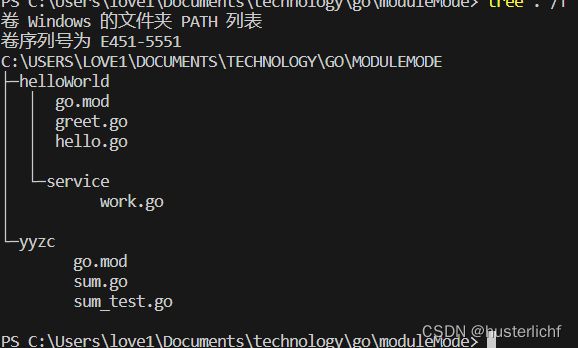
golang --- module-aware 模式下 包引入
一、文件列表如下 其中helloWorld目录是main包(package)所在目录,即该目录下所有的goy源文件(不包含子目录)属于main包,hello.go是mian函数所在文件 二、module-aware 模式启用 开启mod模式 go env -w G…...

从原理到实践 | Pytorch tensor 张量花式操作
文章目录 1.张量形状与维度1.1标量(0维张量):1.2 向量(1维张量):1.3矩阵(2维张量):1.4高维张量: 2. 张量其他创建方式2.1 创建全零或全一张量:2.2…...

无涯教程-JavaScript - TRANSPOSE函数
描述 TRANSPOSE函数将单元格的垂直范围作为水平范围返回,反之亦然。必须将TRANSPOSE函数作为数组公式输入,该范围必须具有与行范围和列范围相同的行和列数。 您可以使用TRANSPOSE在工作表上移动数组或范围的垂直和水平方向。 语法 TRANSPOSE (array)键入函数后,按CTRL SHI…...
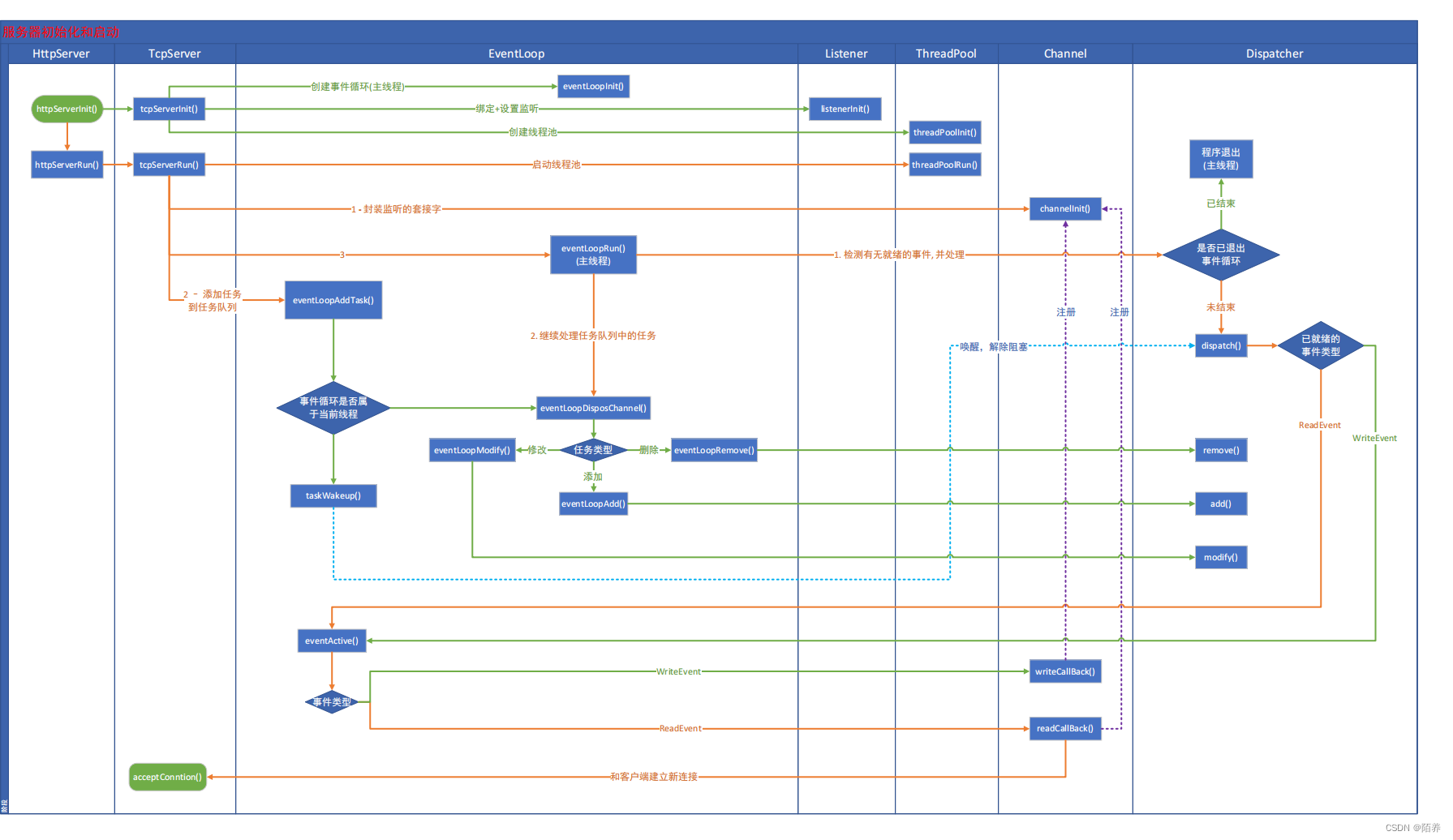
Webserver项目解析
一.webserver的组成部分 Buffer类 用于存储需要读写的数据 Channel类 存储文件描述符和相应的事件,当发生事件时,调用对应的回调函数 ChannelMap类 Channel数组,用于保存一系列的Channel Dispatcher 监听器,可以设置为epo…...

Spring Cloud 篇
1、什么是SpringCloud ? Spring Cloud 流应用程序启动器是基于 Spring Boot 的 Spring 集成应用程序,提供与外部系统的集成。Spring cloud Task,一个生命周期短暂的微服务框架,用于快速构建执行有限数据处理的应用程序。 2、什么…...

vim,emacs,verilog-mode这几个到底是啥关系?
vim:不多说了被各类coder誉为地表最强最好用的编辑器;gvim,gui vim的意思; emacs:也是一个编辑器,类似vscode; vim在使用的时候为了增强其功能,有好多好多插件,都是以.…...

解决npm run build 打包出现XXXX.js as it exceeds the max of 500KB.
问题描述: npm run build 时出现下面的问题: Note: The code generator has deoptimised the styling of D:\base\node_modules\_element-ui2.15.12element-ui\lib\element-ui.common.js as it exceeds the max of 500KB.在项目的根目录加粗样式下找到 …...

Java 抖音小程序SDK
抖音小程序SDK,抖音SDK 码云地址:dy-open-sdk: 字节跳动,抖音小程序sdk...
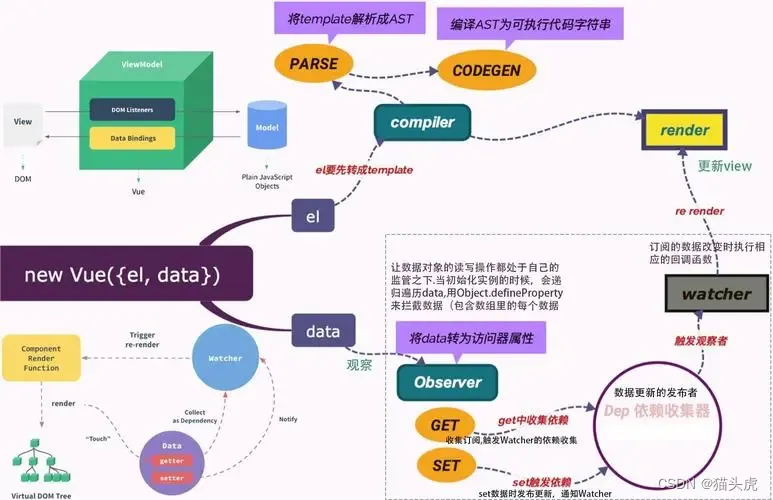
Vue.js的服务器端渲染(SSR):为什么和如何
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

Gin 打包vue或react项目输出文件到程序二进制文件
Gin 打包vue或react项目输出文件到程序二进制文件 背景解决方案1. 示例目录结构2. 有如下问题要解决:3. 方案探索 效果 背景 前后端分离已成为行业主流,vue或react等项目生成的文件独立在一个单独目录,与后端项目无关。 实际部署中,通常前面套…...
深度解析shell脚本的命令的原理之pwd
pwd是Print Working Directory的缩写,是一个Unix和Linux shell命令,用于打印当前工作目录的绝对路径。以下是对这个命令的深度解析: 获取当前工作目录:pwd命令通过调用操作系统提供的getcwd(或相应的)系统调…...

Kafka3.0.0版本——消费者(分区的分配以及再平衡)
目录 一、分区的分配以及再平衡1.1、消费者分区及消费者组的概述1.2、如何确定哪个consumer来消费哪个partition的数据1.3、消费者分区分配策略 一、分区的分配以及再平衡 1.1、消费者分区及消费者组的概述 一个consumer group中有多个consumer组成,一个 topic有多…...
Kotlin文件遍历FileTreeWalk filter
Kotlin文件遍历FileTreeWalk filter import java.io.Filefun main(args: Array<String>) {val filePath "."val file File(filePath)val fileTree: FileTreeWalk file.walk()fileTree//.maxDepth(1) //遍历层级1,不检查子目录.filter {it.isFile…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...

验证redis数据结构
一、功能验证 1.验证redis的数据结构(如字符串、列表、哈希、集合、有序集合等)是否按照预期工作。 2、常见的数据结构验证方法: ①字符串(string) 测试基本操作 set、get、incr、decr 验证字符串的长度和内容是否正…...
