oracle11g忘记system密码,重置密码
OPW-00001: 无法打开口令文件
cmd.exe 使用管理员身份登录
找到xxx\product\11.2.0\dbhome_1\database\PWDorcl.ora文件,删除
执行orapwd file=D:\app\product\11.2.0\dbhome_1\database\PWDorcl.ora password=tiger
(orapwd 在\product\11.2.0\dbhome_1\BIN目录下)
登录system,报错
ORA-28000: the account is locked
详细更改命令如下:
C:\WINDOWS\system32>orapwd file=D:\app\product\11.2.0\dbhome_1\database\PWDorcl.ora password=tiger entries=40 force=y
C:\WINDOWS\system32>sqlplus /nolog
SQL*Plus: Release 11.2.0.1.0 Production on Wed Feb 22 19:45:24 2023
Copyright (c) 1982, 2010, Oracle. All rights reserved.
SQL> conn sys/tiger as sysdba
Connected.
SQL> grant connect to sys identified by tiger;
Grant succeeded.
SQL> alter user SYSTEM account unlock;
User altered.
SQL> grant connect to system identified by tiger;
Grant succeeded.
SQL>alter user scott identified by tiger;
User altered.
参考:
关于Oracle使用管理员账号登录失败的问题
https://www.cnblogs.com/lcword/p/15992907.html
相关文章:

oracle11g忘记system密码,重置密码
OPW-00001: 无法打开口令文件 cmd.exe 使用管理员身份登录 找到xxx\product\11.2.0\dbhome_1\database\PWDorcl.ora文件,删除 执行orapwd fileD:\app\product\11.2.0\dbhome_1\database\PWDorcl.ora passwordtiger (orapwd 在\product\11.2.0\dbhome_1\BIN目录下…...
黑马 Vue 快速入门 笔记
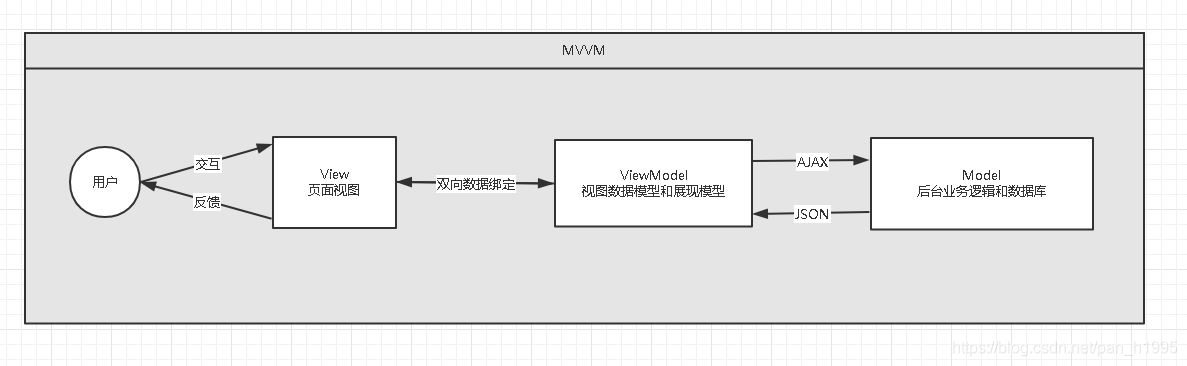
黑马 Vue 快速入门 笔记0 VUE相关了解0.1 概述0.2 MVVM0.3 JavaScript框架0.4 七大属性0.5 el:挂载点1 VUE基础1.0 第一个vue代码:Hello,vue1.1 v-bind 设置元素的属性 简写 :1.2 v-if , v-else , v-else-ifv-if , v-e…...

HTTP协议知识体系核心重点梳理
HTTP协议知识体系核心重点梳理TCP/IP协议1.四层模型2.通信过程3.tcp三次握手和四次挥手4.tcp安全传输4. 一次HTTP通信流程HTTP协议HTTP/1.1CookieHttp报文格式内容编码分块传输编码HTTP状态码重定向状态码常用的通用首部cache-controlExpiresConnectionTransfer-Encoding常用的…...

Nginx优化与防盗链
Nginx优化与防盗链 📒博客主页: 微笑的段嘉许博客主页 💻微信公众号:微笑的段嘉许 🎉欢迎关注🔎点赞👍收藏⭐留言📝 📌本文由微笑的段嘉许原创! Ὄ…...

自动驾驶路径规划概况
文章目录前言介绍1. 路径规划在自动驾驶系统架构中的位置2. 全局路径规划的分类2.1 基础图搜索算法2.1.1 Dijkstra算法2.1.2 双向搜索算法2.1.3 Floyd算法2.2 启发式算法2.2.1 A*算法2.2.2 D*算法2.3 基于概率采样的算法2.3.1 概率路线图(PRM)2.3.2 快速…...

某某银行行面试题目汇总--HashMap为什么要扩容
一、HashMap啥时候扩容,为什么扩容? HashMap的默认大小是16。在实际开发过程中,我们需要去存储的数据量往往是大于存储容器的默认大小的。所以,出现容量默认大小不能满足需求时,就需要扩容。而这个扩容的动作是由集合自…...
求职者:“我有五年测试经验”面试官: “不,你只是把一年的工作经验用了五年”
最近看到很多软件测试由于公司裁员而需要重新求职的。他们普遍具有4年甚至更长的工作经验。但求职结果往往都不太理想。 我在与部分软件测试求职者交谈的过程中发现,很多人的工作思路不清晰,技能不扎实,没有持续学习的习惯,但对于…...
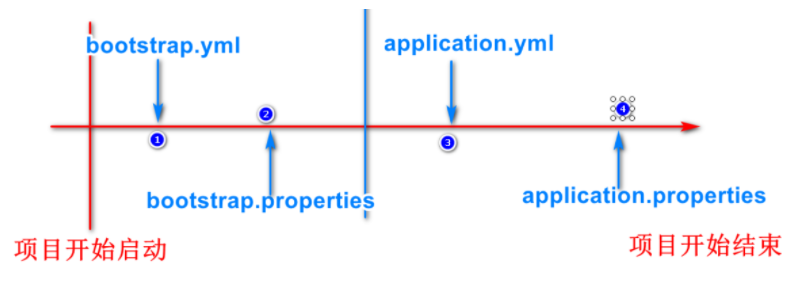
Nacos配置中心
什么是配置中心所谓配置中心:在微服务的环境下,将项目需要的配置信息保存在配置中心,需要读取时直接从配置中心读取,方便配置管理的微服务工具我们可以将部分yml文件的内容保存在配置中心一个微服务项目有很多子模块,这些子模块可能在不同的服务器上,如果有一些统一的修改,我们…...

【故障】6、yum不可用
文章目录[toc]一、yum命令不能使用1)报错2)问题分析3)完全删除python及yum重新安装1、删除python2、删除yum3、下载Python依赖rpm包4、下载yum依赖rpm包5、强制安装python6、强制安装yum7、测试一、yum命令不能使用 1)报错 Ther…...

深度解读 | 数据资产管理面临诸多挑战,做好这5个措施是关键
日前,大数据技术标准推进委员会(中国通信标准化协会下(CCSA)的专业技术委员会,简称TC601)发布《数据资产管理实践白皮书》(6.0 版)(以下简称:报告)…...
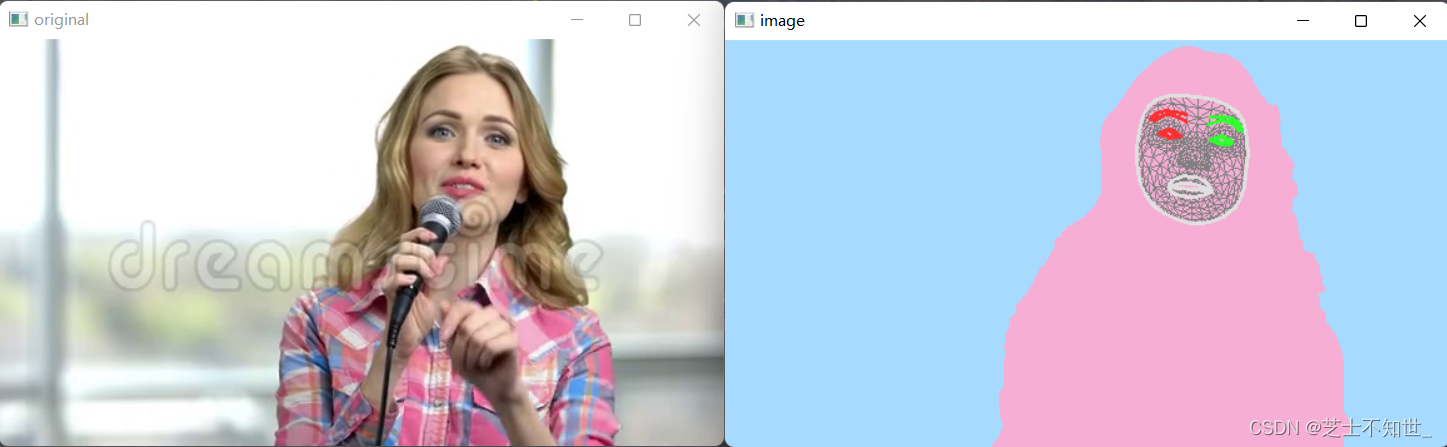
双检测人脸防伪识别方法(活体检测+人脸识别+关键点检测+人像分割)
双检测人脸防伪识别=人脸检测+活体检测+人脸识别 1.人脸关键点+语义分割 使用mediapipe进行视频人脸关键点检测和人像分割: import time import cv2 import mediapipe as mp import numpy as npmp_drawing = mp.solutions.drawing_utils mp_drawing_styles = mp.solution…...

2023年3月 - 笔记
内容已复习 采用下划线标识内容已重写 并补充优化 新建文章并添加超链接 背景颜色 绿色 Python 2023年3月1日 Python 把列表转成元组 # 1、Python 把列表转成元组 使用tuple 即可 list_a [1, 2, 3, 4, 5, 6] list_b tuple(list_a) print(list_b)# 2、如果想把 元组转成列…...
浅谈Redisson实现分布式锁对原理
1.Redisson简介 Redis 是最流行的 NoSQL 数据库解决方案之一,而 Java 是世界上最流行(注意,我没有说“最好”)的编程语言之一。虽然两者看起来很自然地在一起“工作”,但是要知道,Redis 其实并没有对 Java…...

struts1.2升级struts2.5.30问题汇总
严重: 配置应用程序监听器[org.apache.struts2.tiles.StrutsTilesListener]错误java.lang.NoClassDefFoundError: org/apache/tiles/web/startup/AbstractTilesListenerat java.lang.ClassLoader.defineClass1(Native Method)at java.lang.ClassLoader.defineClass(ClassLoader…...

电动汽车充放电的优化调度(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
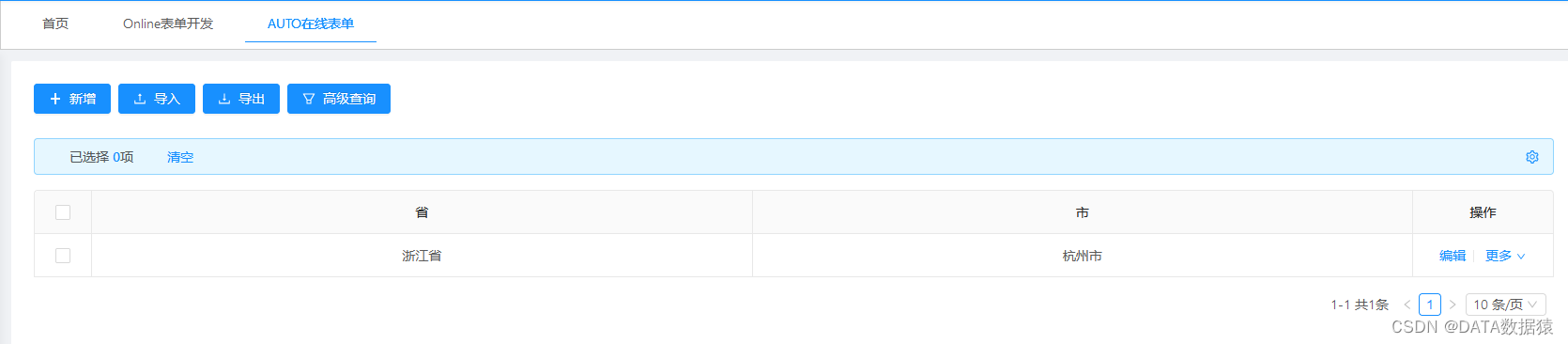
《JeecgBoot系列》 如何设计表单实现“下拉组件二级联动“ ? 以省市二级联动为例
《JeecgBoot系列》 如何设计表单实现"下拉组件二级联动" ? 以省市二级联动为例 一、准备字典表 1.1 创建字典表 CREATE TABLE sys_link_table ( id int NULL, pid int NULL, name varchar(64) null );1.2 准备数据 idpidname1全国21浙江省32杭州市42宁波市51江苏…...
数学小课堂:数学的线索(从猜想到定理再到应用的整个过程)
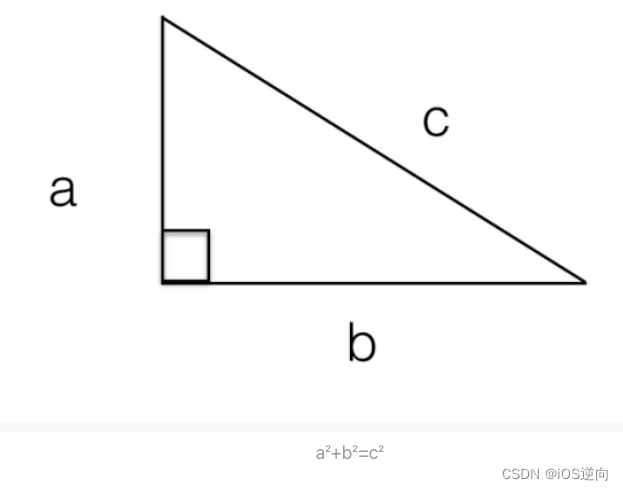
文章目录 引言I 勾股定理1.1 勾三股四弦五1.2 数学和自然科学的三个本质差别1.3 总结引言 从猜想到定理再到应用的整个过程是数学发展和体系构建常常经历的步骤。 I 勾股定理 勾股定理: 直角三角形两条直角边的平方之和等于斜边的平方,这个定理在国外都被称为毕达哥拉斯定理…...
Collecting package metadata (current_repodata.json): failed
一、问题描述 安装anaconda之后,想创建环境,用了下面这段代码: conda create -n pytorch python3.7 conda创建环境报错了,报了如下这一堆: Collecting package metadata (current_repodata.json): failedUnavailab…...
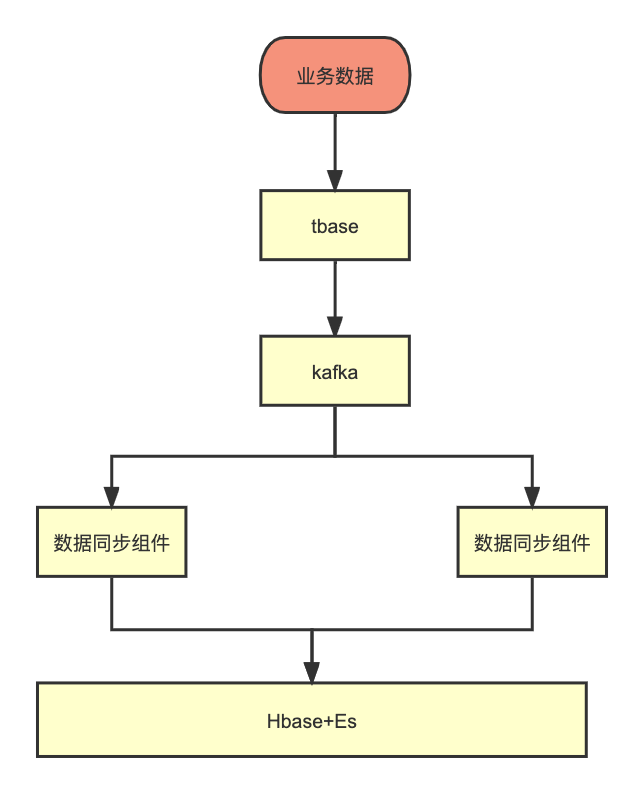
几十亿工单表,查询优化案例
前言: 之前在某大型保险公司担任技术经理,负责优化话务系统模块,由于系统已经运行10年之久,尤其在话务系统中,沉积了几十亿的话务信息表,业务人员反馈,话务系统历史数据查询部分已经完全查询不动࿰…...
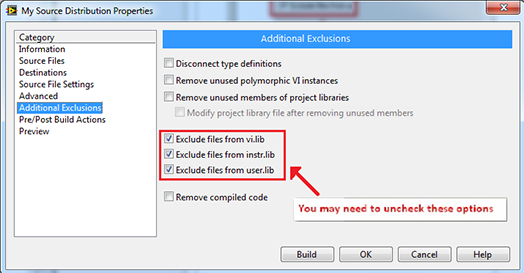
LabVIEW应用程序(EXE)无法正确动态调用插件
LabVIEW应用程序(EXE)无法正确动态调用插件正在构建一个应用程序并使用插件架构,以便可以动态调用将来创建的VI(插件)。应用程序在LabVIEW开发环境中可以正常运行,但不能作为可执行程序运行。运行可执行文件…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...
