两阶段鲁棒优化matlab实现——CCG和benders
目录
1 主要内容
2 部分代码
3 程序结果
4 程序链接
1 主要内容
程序采用matlab复现经典论文《Solving two-stage robust optimization problems using a column-and-constraint generation method》算例,实现了C&CG和benders算法两部分内容,通过对比学习能够方便掌握两种算法的编程要点,深入了解C&CG算法优势,对于学习鲁棒优化是不可多得的资料,程序均采用matlab+cplex求解!

2 部分代码
y = binvar(3,1);
z = sdpvar(3,1);
x =sdpvar(9,100,'full');
eta = sdpvar(1);
g = sdpvar(3,1);
pi = sdpvar(size(G,1),1);
v=binvar(size(G,1),1);
w=binvar(size(G,2),1);
%% CCG
LB=-inf; UB=inf; iter=1; BigM=1e5;
MP_Cons = [ 0<=z<=800*y, 772<=sum(z), b'*x(:,iter)<=eta, 0<=x(:,iter) ];
MP_Obj = coe1*y +coe2*z+eta ;
ops = sdpsettings('solver','cplex','verbose',0);
Uncertain_Cons=[ 0<=g<=1, sum(g)<=1.8, g(1)+g(2)<=1.2 ];
while abs(UB-LB) >1e-5disp(['迭代第',num2str(iter),'次'])optimize(MP_Cons,MP_Obj,ops);LB = max(LB, value(MP_Obj)); % LBSP_Obj = b'*x(:,iter) ;SP_Cons = [ Uncertain_Cons, 0<=x(:,iter), G*x(:,iter)>=h-E*[value(y);value(z)]-M*g ];SP_Cons = [SP_Cons, 0<=pi, G'*pi<=b ];SP_Cons = [SP_Cons, G*x(:,iter)-h+E*[value(y); value(z)]+M*g <= BigM*(1-v) ];SP_Cons = [SP_Cons, pi<=BigM*v];SP_Cons = [SP_Cons, b-G'*pi <= BigM*(1-w) ];SP_Cons = [SP_Cons, x(:,iter)<=BigM*w ]; sol_SP=optimize(SP_Cons,-SP_Obj,ops);if sol_SP.problem==0 % SP is solvedUB=min(UB, coe1*value(y)+coe2*value(z)+value(SP_Obj)); % UBdisp([' g = ',num2str(value(g)')]);endMP_Cons = [MP_Cons, 0<=x(:,iter+1), b'*x(:,iter+1)<= eta, G*x(:,iter+1)>=h- E*[y;z]-M*value(g) ];iter = iter+1;display([' LB: ',num2str(LB), ' UB: ',num2str(UB),]);
end
3 程序结果
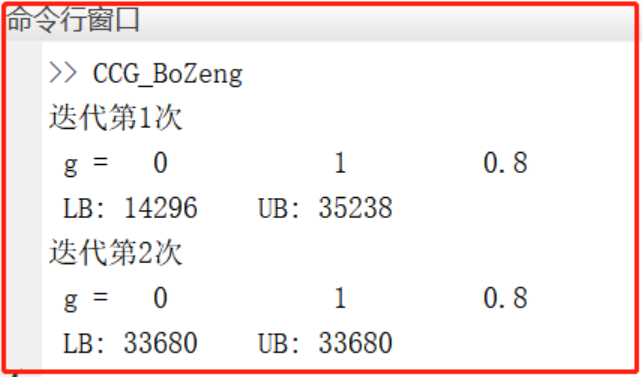
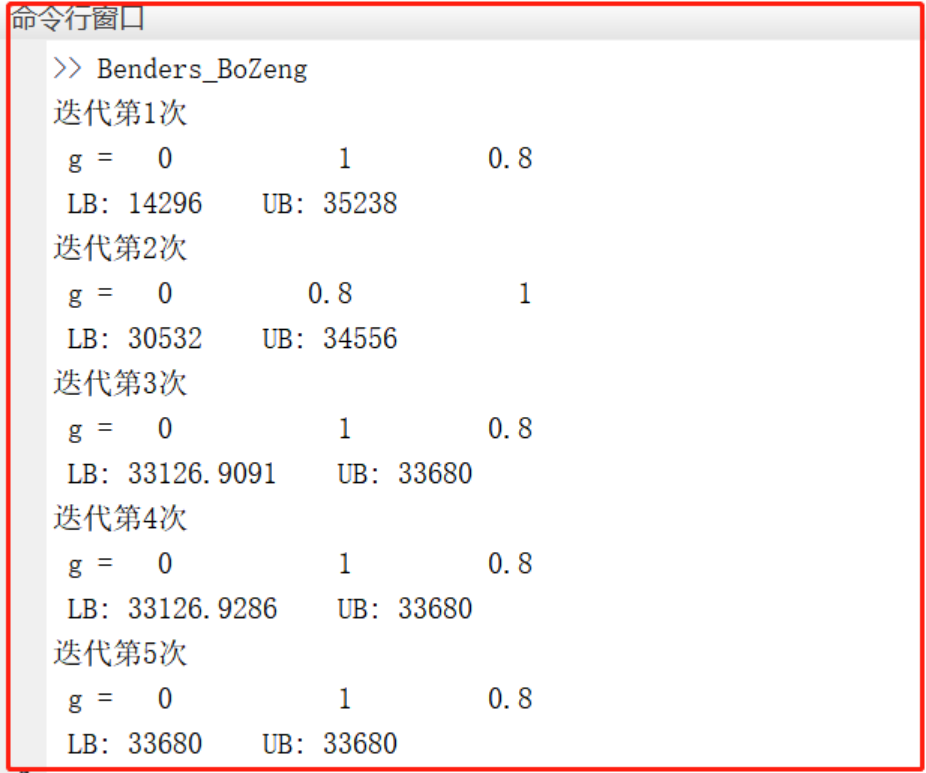
4 程序链接
【免费】两阶段鲁棒优化matlab实现——C&CG和benders
相关文章:

两阶段鲁棒优化matlab实现——CCG和benders
目录 1 主要内容 2 部分代码 3 程序结果 4 程序链接 1 主要内容 程序采用matlab复现经典论文《Solving two-stage robust optimization problems using a column-and-constraint generation method》算例,实现了C&CG和benders算法两部分内容,通过…...

二进制安全虚拟机Protostar靶场(4)写入shellcode,基础知识讲解 Stack Five
前言 这是一个系列文章,之前已经介绍过一些二进制安全的基础知识,这里就不过多重复提及,不熟悉的同学可以去看看我之前写的文章 二进制安全虚拟机Protostar靶场 安装,基础知识讲解,破解STACK ZERO https://blog.csdn.net/qq_45894840/artic…...
【Flink实战】玩转Flink里面核心的Source Operator实战
🚀 作者 :“大数据小禅” 🚀 文章简介 :【Flink实战】玩转Flink里面核心的Source Operator实战 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 目录导航 Flink 的API层级介绍Source Operator速览Flin…...

[2023-09-12]Oracle备库查询报ORA-01187
一个多表关联的语句在备库执行查询时提示ORA-01187: cannot read from file because it failed verification tests,单独对某一个表查询则正常返回(因为不需要排序等,没有用到临时表空间)。 查看报错信息发现是提示的临时数据文件…...

leetcode 16.最接近的三数之和
给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。 返回这三个数的和。 假定每组输入只存在恰好一个解。 示例 1: 输入:nums [-1,2,1,-4], target 1 输出:…...

antd table 自定义排序图标
要在Ant Design的Table组件中自定义排序图标,可以使用sorter和sortDirections属性来实现自定义排序逻辑和图标。以下是一个示例,演示如何在Ant Design的Table中自定义排序图标: import React, { useState } from react; import { Table, Spa…...
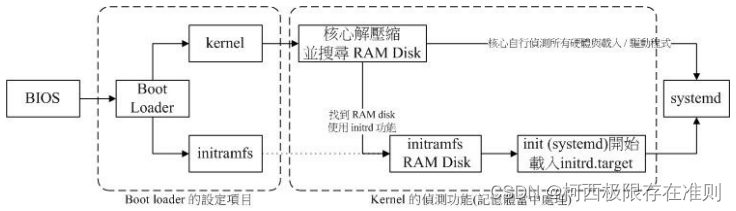
第十九章、【Linux】开机流程、模块管理与Loader
19.1.1 开机流程一览 以个人计算机架设的 Linux 主机为例,当你按下电源按键后计算机硬件会主动的读取 BIOS 或 UEFI BIOS 来载入硬件信息及进行硬件系统的自我测试, 之后系统会主动的去读取第一个可开机的设备 (由 BIOS 设置的) …...
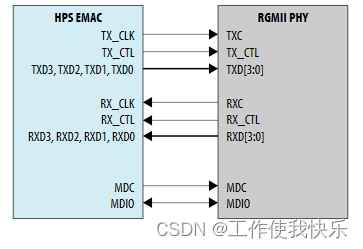
GMAC PHY介绍
1.1PHY接口发展 (1)MII支持10M/100Mbps,一个接口由14根线组成,它的支持还是比较灵活的,但是有一个缺点是因为它一个端口用的信号线太多。参考芯片:DP83848 、DM900A(该芯片内部集成了MAC和PHY接…...

华为OD机考算法题:最远足迹
目录 题目部分 解读与分析 代码实现 题目部分 题目最远足迹难度易题目说明某探险队负责对地下洞穴进行探险。 探险队成员在进行探险任务时,随身携带的记录器会不定期地记录自身的坐标,但在记录的间隙中也会记录其他数据。探索工作结束后,…...

QScrollBar滚动条、QSlider滑块、 QDial表盘
QAbstractSlider 类、 QSCrollBar 类、 QSlider 类 一、 基本原理 1、 QAbstractSlider 继承自 QWidget,该类主要用于提供一个范围内的整数值, 2、 QAbstractSlider 类是 QScrollBar 类(滚动条)、 QSlider 类(滑块)、 QDial 类(表盘)的父类,因…...
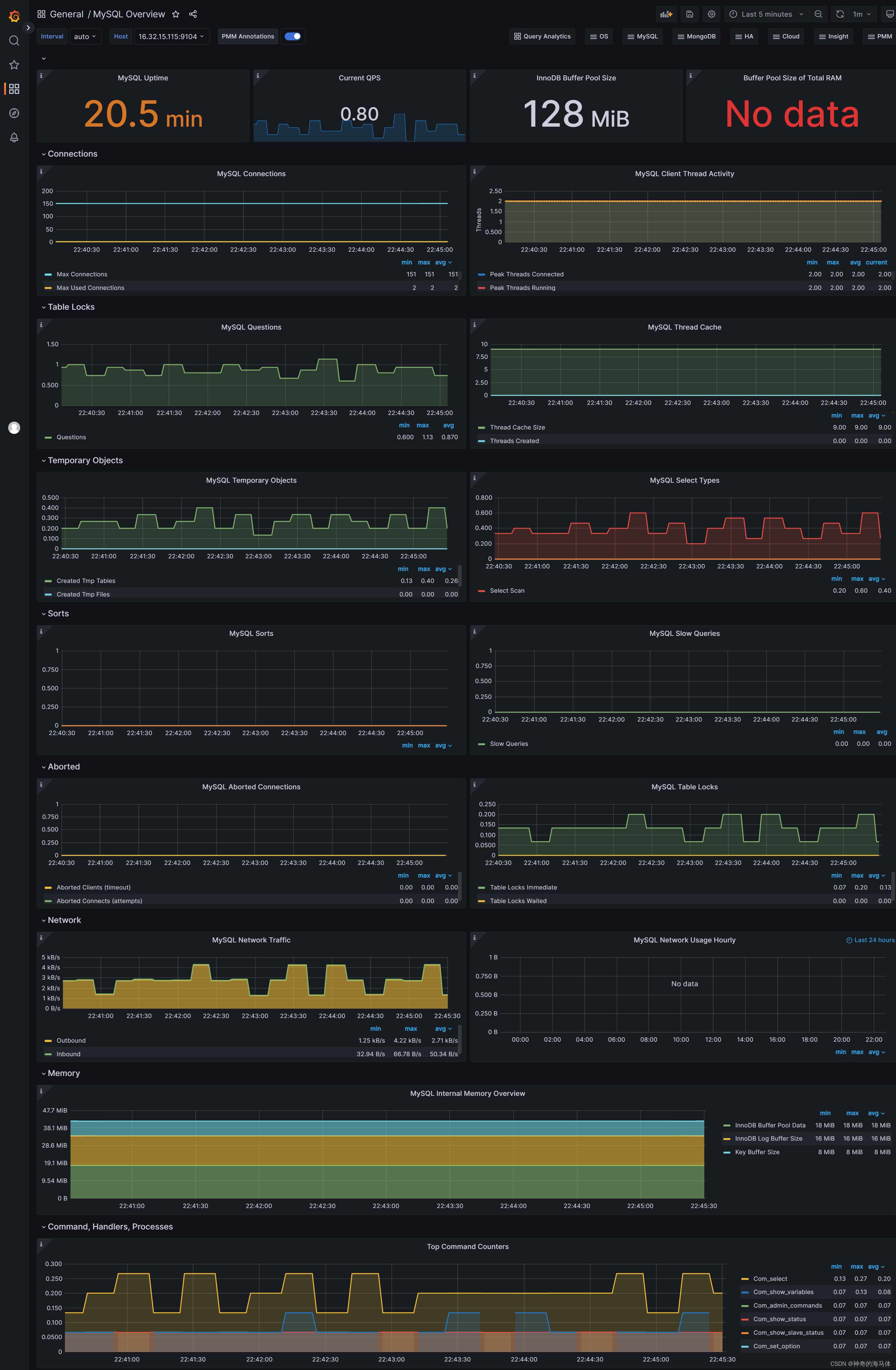
Prometheus+Grafana可视化监控【MySQL状态】
文章目录 一、安装Docker二、安装MySQL数据库(Docker容器方式)三、安装Prometheus四、安装Grafana五、Pronetheus和Grafana相关联六、安装mysqld_exporter七、Grafana添加MySQL监控模板 一、安装Docker 注意:我这里使用之前写好脚本进行安装Docker,如果…...
)
五,编译定制rom并刷机实现硬改(二)
系列文章目录 第一章 安卓aosp源码编译环境搭建 第二章 手机硬件参数介绍和校验算法 第三章 修改安卓aosp代码更改硬件参数 第四章 编译定制rom并刷机实现硬改(一) 第五章 编译定制rom并刷机实现硬改(二) 第六章 不root不magisk不xposed lsposed frida原生修改定位 第七章 安卓…...

Modbus协议详解3:数据帧格式 - RTU帧 ASCII帧的区别
Modbus既然是一种通信协议,那它就应该有规定的通信格式用于在设备之间的指令接收与识别。 本文就着重讲讲Modbus协议的RTU帧和ASCII帧。 Modbus帧在串行链路上的格式如下: 在上图的格式中: 1)地址域:指代的是子节点地址…...

认识数据分析
文章目录 1. 认识数据分析1.1 数据自身的三大属性1.2 建数仓 数据分析的工程技术1.3 数据分析解决问题的原理1.4 数据分析的具体流程1.5 数据的中心化和智能化1.6 数据分析的四种类型和六个方向 1. 认识数据分析 1.1 数据自身的三大属性 客观:用数字衡量和表现一件…...

Learn Prompt-ChatGPT 精选案例:写作博客
在 ChatGPT 的帮助下,文本内容的产出,尤其是撰写博客文章的过程得到了进一步的简化。你可以让 ChatGPT 激发你的灵感,也可以让它美化你的文章内容。 这里我们希望能通过prompt写出一篇以“ChatGPT对社会各行各业的影响”为主题的博客。 本页…...

《确保安全:PostgreSQL安全配置与最佳实践》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖: 🛠️ 全栈技术 Full Stack: 📚…...

Unity中Shader抓取屏幕并实现扭曲效果
文章目录 前言一、屏幕抓取,在上一篇文章已经写了二、实现抓取后的屏幕扭曲实现思路:1、屏幕扭曲要借助传入 UV 贴图进行扭曲2、传入贴图后在顶点着色器的输入参数处,传入一个 float2 uv : TEXCOORD,用于之后对扭曲贴图进行采样3、…...

深浅拷贝详解
深浅拷贝 经典真题 深拷贝和浅拷贝的区别?如何实现 深拷贝和浅拷贝概念 首先,我们需要明确深拷贝和浅拷贝的概念。 浅拷贝:只是拷贝了基本类型的数据,而引用类型数据,复制后也是会发生引用,我们把这种拷…...

@Scheduled 定时任务
Scheduled(cron"30 * * * * ?") 1.cron表达式格式: {秒数} {分钟} {小时} {日期} {月份} {星期} {年份(可为空)} 2.cron表达式各占位符解释: {秒数}{分钟} > 允许值范围: 0~59 ,不允许为空值,若值不合法,调度器将…...

丙烯酸共聚聚氯乙烯树脂
声明 本文是学习GB-T 42790-2023 丙烯酸共聚聚氯乙烯树脂. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 1 范围 本文件规定了丙烯酸共聚聚氯乙烯树脂的外观、物化性能等技术要求,描述了相应的采样、试验方 法、检验规则、标志、包装、…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...
Element-Plus:popconfirm与tooltip一起使用不生效?
你们好,我是金金金。 场景 我正在使用Element-plus组件库当中的el-popconfirm和el-tooltip,产品要求是两个需要结合一起使用,也就是鼠标悬浮上去有提示文字,并且点击之后需要出现气泡确认框 代码 <el-popconfirm title"是…...

P10909 [蓝桥杯 2024 国 B] 立定跳远
# P10909 [蓝桥杯 2024 国 B] 立定跳远 ## 题目描述 在运动会上,小明从数轴的原点开始向正方向立定跳远。项目设置了 $n$ 个检查点 $a_1, a_2, \cdots , a_n$ 且 $a_i \ge a_{i−1} > 0$。小明必须先后跳跃到每个检查点上且只能跳跃到检查点上。同时࿰…...
