算法通过村第七关-树(递归/二叉树遍历)青铜笔记|手撕递归
文章目录
- 前言
- 1. 递归的特征
- 2. 如何写出好的递归
- 3. 怎么看懂递归的代码
- 总结
前言
提示:我们生活在24小时不眠不休的社会里但是没有24小时不眠不休的身体有些东西必须舍弃 -- 马特·海格
这一关,我看要谈论的是递归问题,说到它就牵扯到很多问题了
- 与树和二叉树的相关问题
- 二分查找相关问题
- 快速排序和并轨排序问题
- 回溯问题
- 动态规划问题
这一切都是递归算法为基础的,当然这一关也是必须掌握的。
1. 递归的特征
递归,大部分都知道是怎么回事,但是就是写不出代码来,此所谓“你讲的都对,但是我就不会”,递归的本质仍是方法的调用,不过是自己调用自己搞,系统给我们维护了不同调用之间的保存和返回的功能。
比如这个故事:
从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,故事讲的是从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,故事讲的是从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,故事讲的是从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,故事讲的是从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,故事讲的是从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,故事讲的是从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,故事讲的是从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,故事讲的是从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,故事讲的是从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事,故事讲的是从前有座山,山上有座庙,庙里有个老和尚,老和尚在给小和尚讲故事······

如果看递归的结构,就像下面的这个样子,前面的一层取一摸一样的调用下一层,不同的只是输入和输出参数,这个递归过程是写递归的一个核心问题。
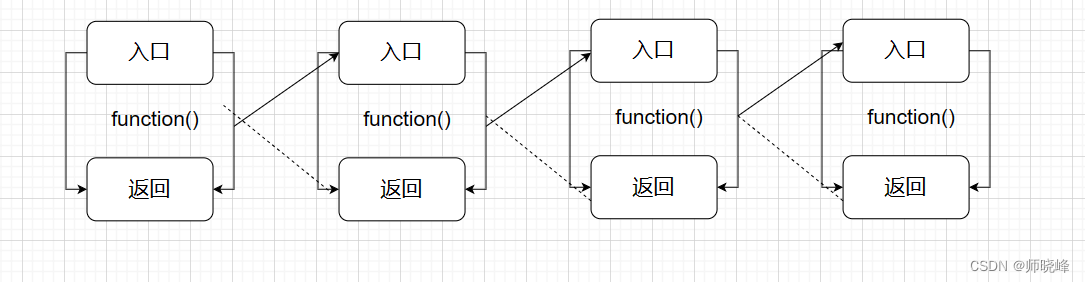
当然这个过程不能一致持续下去,一定要在满足某个要求之后返回结果,否则的话就会抛出我们常见的“StackOverFlow”的问题。
所有的递归有两个必要的特征:
- 执行时范围不断缩小,这样才能触底反弹
- 种植判断在调用递归的前面
理解这个,是我们掌握递归的辅助工具,我们一一分析:
- 执行范围不断缩小
递归在数学里的概念是递推,设计递归就是努力寻找数学里的递推公式。经典的问题就是求阶乘,好多同学也是通过这个认识递归的吧,那时我们第一次见面。 还记得递推公式吗? f(n) = f(n-1) * n,很显然一定是触底之后才能反弹的,再比如就是典型的斐波那契数列递推公式了,f(n) = f(n -1) + f(n - 2);当然n也是在不断的缩小。这条规律可以辅助我们检查自己写的递推公式对不对。
再比如后面我们会遇到青蛙跳台阶问题,他的递推公式f(n) = f(n -1) + f(n - 2);你想奇怪呀?怎么会一样呢,没错,他就一样🤣。
范围缩小不一定只体现在n的变化上,在树的递归中,我们会大量的接触到类似这样的结构:
int leftDepth = getDepth(node.left); // 左
int rightDepth = getDepth(node.right); // 右
每一次递归,都是在将范围缩小到当前节点的左子树或者右子树,范围也是在不断的缩小的。
- 终止条件判断在递归调用的前面
递归之后可能还有终止条件,但是在执行递归之前,一定会有一个终止条件。这个条件可以帮助我么你检查自己写的算法对不对。
为什么呢?我们看个例子🌰:
很显然recursion()会不断的调用自己,这样一直递归下去,就无法退出来,知道抛出堆栈溢出异常(StackOverFlowError)。
public void recursion(参数0) {recursion(参数1);if(终止条件) {return ;}
}
所以:任何递归方法在执行之前,一定会有一个终止条件
实际上一个方法里的递归调用可能不止一次,还会加一些逻辑处理,比如下面这样,但是终止的条件仍然在前面。
public void recursion(参数0) {if(终止条件) {return ;}// 逻辑一recursion(参数1);// 逻辑二recursion(参数2);// ......recursion(参数n);可能还有其他一些逻辑运算
}
这一特点启示我们,可以先考虑在什么条件下终止,而相关代码要写在靠前的位置,之后再考虑递归的逻辑,这样可以很好的降低编写代码的难度。
2. 如何写出好的递归
明白了上面的道理,那么你就右疑问了,怎么写出好的递归方法呢?
- 从小到大递推
递归该怎么写?递归源于数学里的归纳法,这个在高中数学里面有的。大致呢?你先猜出存在的递归关系,f(n) = pf(n-1),然后你只要证明当n增加1时,f(n + 1) = pf(n)也是成立的就说明你的猜想没有问题。不过在算法里面,我们写递归一般不需要证明,我么你先挑选几个较小的值验证一下,然后再选择几个较大的值验证一下就可以了。
很显然大部分从n = 1,2,3或者只有一两个元素开始写最简单。典型的就是斐波那契数列为 1 1 2 3 5 8 …,从 n = 3开始都满足f(n) = f(n - 1) + f(n -2),然后我们再选择某个比较大的n来验证就可以了。
所以-这就是我们要找的递推公式:
f(n) = f(n - 1) + f(n -2)
对于阶乘来说也一样
n == 1 f(1) = 1
n == 2 f(2) = 2 * f(1) = 2
n == 3 f(3) = 3 * f(2) = 6
n == 4 f(4) = 4 * f(3) = 24
...
由此我们可以推测递推公式:f(n) = n * f(n - 1)。
- 分情况讨论,明确结束条件
我们说过递归里面的终止条件一定时靠前的,而大部分递归的终止条件不是n最小开始出低反弹时有几种情况:
对于阶乘,当n == 1 时你就知道f(1) = 1,也就是下面这个样子:
// 算 n 的阶乘(假设n != 0)
int f(n) {if(n == 1){return 1;}
}
有时候要考虑的终止条件不知一个,例如斐波那契数列的递推公式f(n) = f(n -1) + f(n - 2)里面,如果n = 2 即 f(2) = f(1) + f(0),很显然这里面没有f(0),所以我们也要将 n == 2 也给限制住,所以结果就变成如下这样:
int f(n) {if(n <= 2){return 1;}
}
有些情况不一定触底才开始反弹,而是达到某种要求就要停止,这样需要考虑的情况会比较多。解决这类问题最直接的方法就是枚举,可以将所有情况列举出来,然后再一一去优化。
只有列举清楚了才可能将终止条件写完整,所以在面试的情况下,不要上来就写,而是和面试官讨论你的设计方案,不要害怕和面试官讨论,假如有很明显的缺陷他也甚至提醒你一下,所以这也是一个借力打力的一个技巧。
确定终止条件队递归至关重要,后面很多题目会话很大的篇幅来分析怎么判断终止条件,一旦判断完毕,递推关系就是水到渠成了。
- 组合成完整的方法
将递推公式和终止条件组合起来,变成完整的方法。
递归经常能看出很多骚操作代码,不要迷信呀,分情况逐个先写出来,之后再看看能否精简优化,不要一个步子迈得太大,容易出事故。我们还是那上面的例子举例,完善我们的代码:
// 算 n 的阶乘(假设n != 0)
int factorial(n) {if(n == 1){return 1;}rerurn n * factorial(n - 1);
}
// 斐波那契数列
int factorial(n){// 1. 先写递归结束条件if(n <= 2){return 1;}// 2. 接着写等价关系式return factorial(n - 1) + factorial(n - 2);
}
每次写递归,都要多方面考虑,后面我们写的时候要注意。
入参和出参??埋坑
3. 怎么看懂递归的代码
对很多人来说,递归最大的问题在于给了答案,看不懂代码,而递归的代码也贼难调试,其实一个转换一下思路就很好解决了。
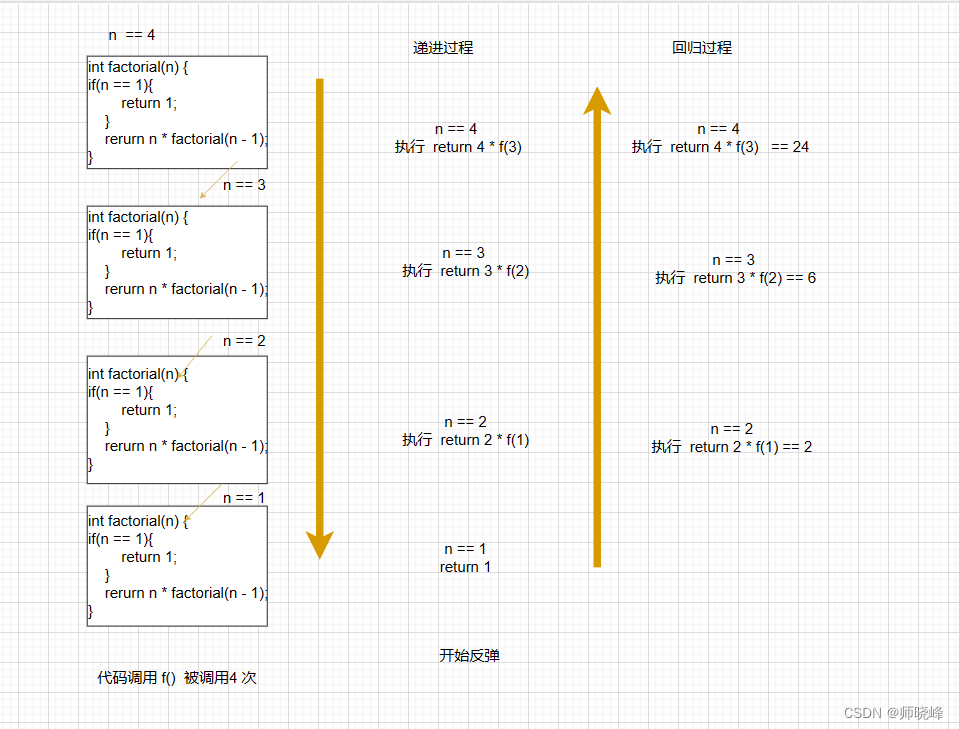
我们先思考一个问题,上面的阶乘,如果n == 4 ,调用了几次上面的f()方法呢?很显然是4次。这个就是递归的一个特征【不撞南墙不回头】,n == 4,3,2是会继续递归,知道有1是满足条件退出,然后就return 1,不再递归了,而且是不断返回上一层并计算。
接着再看返回时每层参数的问题,递归本质上仍然是方法调用,所以可以按照方法调用的方式来检验写的对不对。
下面是一个完整的思路,你会发现递归不归是一个方法被调用了好几次,而每次n都在减小,这就是递归的过程,触底之后,也就是满足终止条件后就开始返回了。
递归的时候当前层的n被系统给保存,而返回的时候会自动设置会来,一次每层n是不一样的,所以就是重新拿到当前这一层n的值完成计算即可。
f(4)阶乘的过程如下:
总结
提示:递归思路,递归的图解,怎么写好递归
相关文章:

算法通过村第七关-树(递归/二叉树遍历)青铜笔记|手撕递归
文章目录 前言1. 递归的特征2. 如何写出好的递归3. 怎么看懂递归的代码总结 前言 提示:我们生活在24小时不眠不休的社会里但是没有24小时不眠不休的身体有些东西必须舍弃 -- 马特海格 这一关,我看要谈论的是递归问题,说到它就牵扯到很多问题了…...
#循循渐进学51单片机#点亮你的LED#not.2
1、深刻理解电容的意义,并且在今后的电路学习过程中要多多注意参考别人电路中去耦电路的处理方法,积累经验。 1)电容缓冲电压,抗电磁干扰; 2)低频率电容,一般用的最多的是钽电容,电…...
基于Java+SpringBoot+Vue+uniapp点餐小程序(亮点:协同过滤算法、会员系统,购物车结算、在线聊天)
校园点餐小程序 一、前言二、我的优势2.1 自己的网站2.2 自己的小程序(小蔡coding)2.3 有保障的售后2.4 福利 三、开发环境与技术3.1 MySQL数据库3.2 Vue前端技术3.3 Spring Boot框架3.4 微信小程序 四、功能设计4.1 系统功能结构设计4.2 主要功能描述 五…...
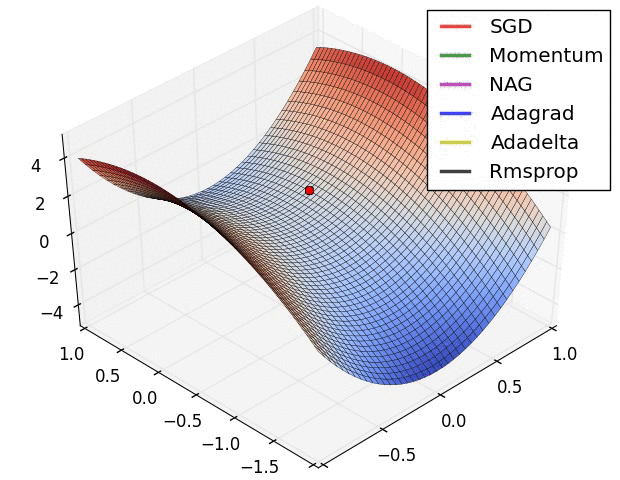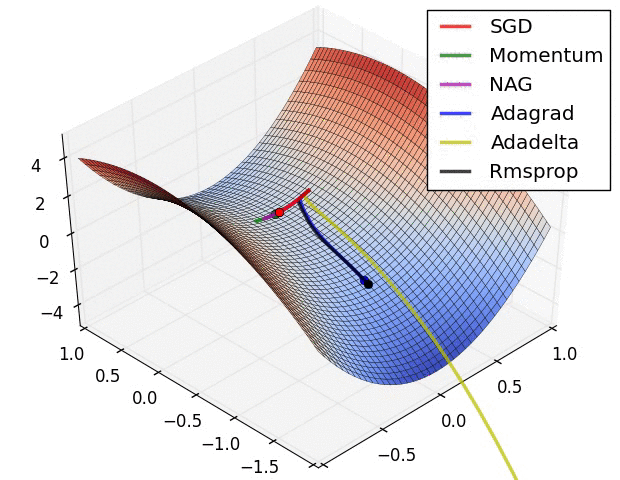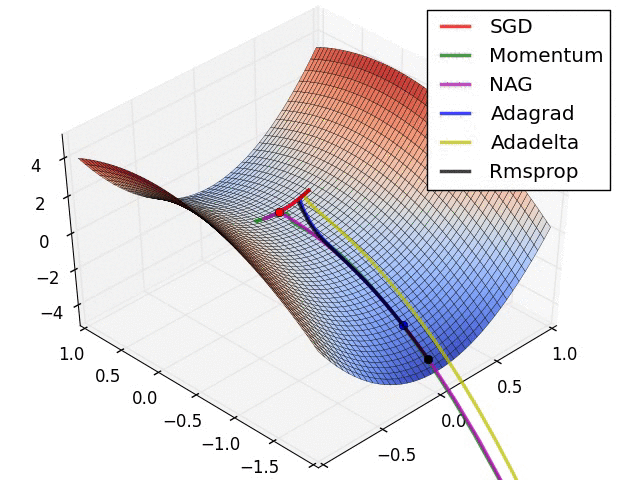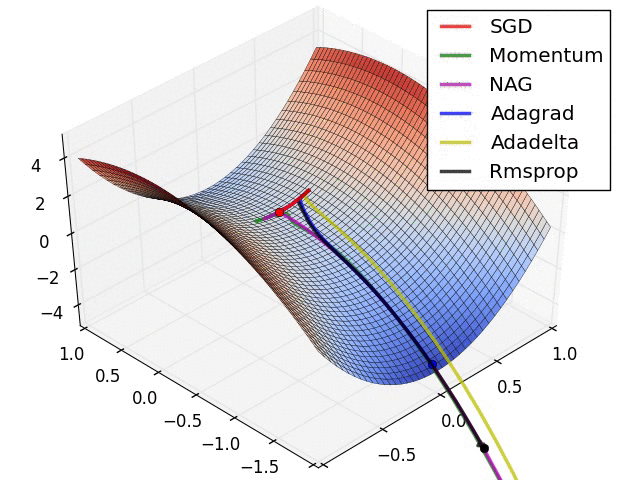
深度学习-全连接神经网络-详解梯度下降从BGD到ADAM - [北邮鲁鹏]
文章目录 参考文章及视频导言梯度下降的原理、过程一、什么是梯度下降?二、梯度下降的运行过程 批量梯度下降法(BGD)随机梯度下降法(SGD)小批量梯度下降法(MBGD)梯度算法的改进梯度下降算法存在的问题动量法(Momentum)目标改进思想为什么有效动量法还有什么效果&…...
数据结构--二叉排序树
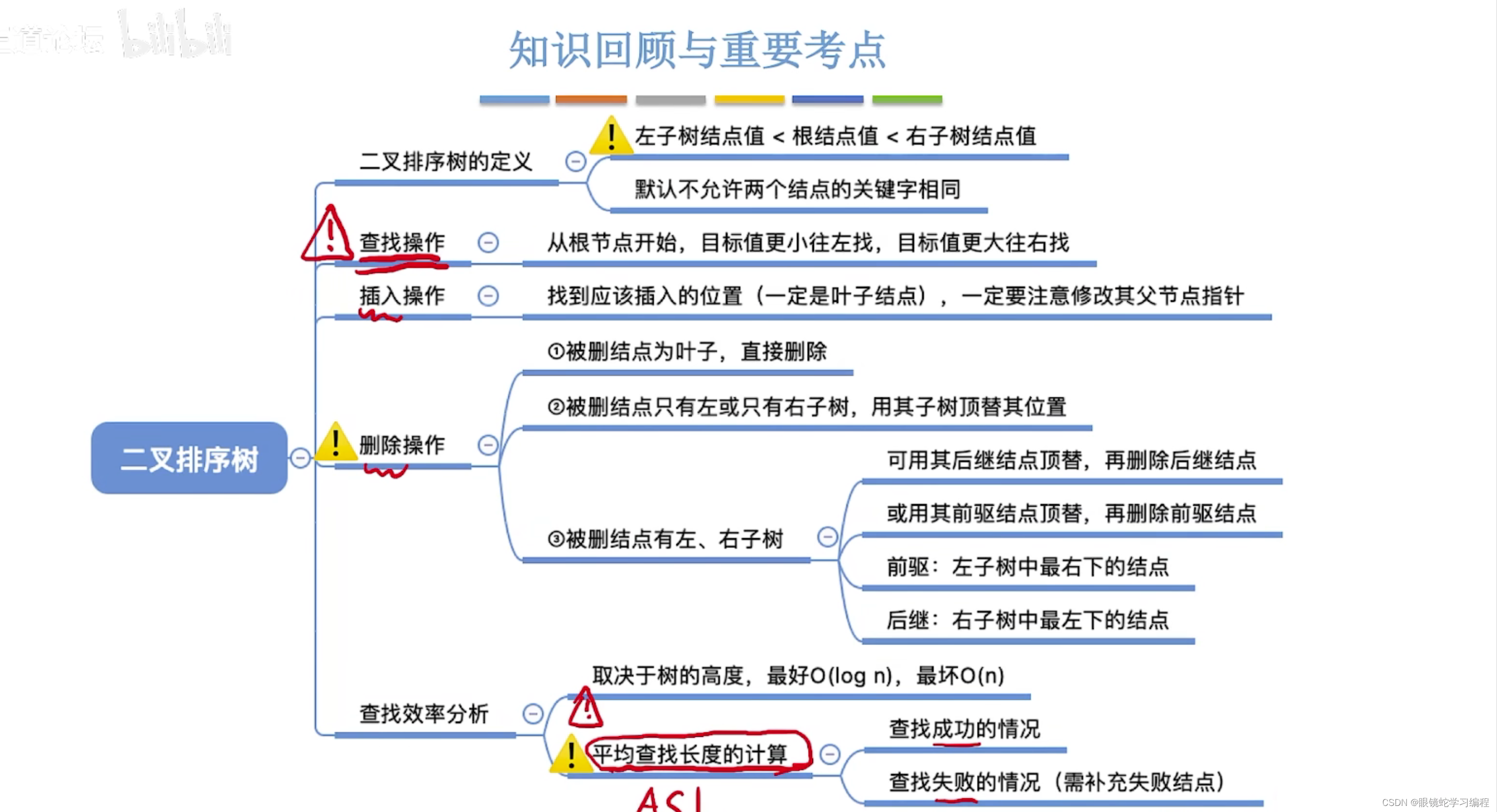
目录 二叉排序树的定义 二叉排序树的查找 二叉排序树的插入 二叉排序树的构造 二叉排序树的删除 查找效率分析 回顾 二叉排序树的定义 二叉排序树的查找 查找成功的情况 查找失败的情况 二叉排序树的插入 注意 (1)二叉排序树不允许出现重复的值…...

Python | 根据子列表中的第二个元素对列表进行排序
在本文中,我们将学习如何根据主列表中存在的子列表的第二个元素对任何列表进行排序。 比如 Input : [[‘rishav’, 10], [‘akash’, 5], [‘ram’, 20], [‘gaurav’, 15]] Output : [[‘akash’, 5], [‘rishav’, 10], [‘gaurav’, 15], [‘ram’, 20]] Input …...

qsort函数详细讲解以及利用冒泡排序模拟实现qsort函数
个人主页:点我进入主页 专栏分类:C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶 C语言刷题 欢迎大家点赞,评论,收藏。 一起努力,一起奔赴大厂。 目录 1.qsort函数 1.1qsort函数的参数 …...

C++QT day6
1> 将之前定义的栈类和队列类都实现成模板类 栈: #include <iostream> #define MAX 128 using namespace std; template<typename T> class Stack_s { private:T *pnew T[MAX];//栈的数组int top;//记录栈顶的变量 public://构造函数Stack_s(int t…...
List与ArrayList
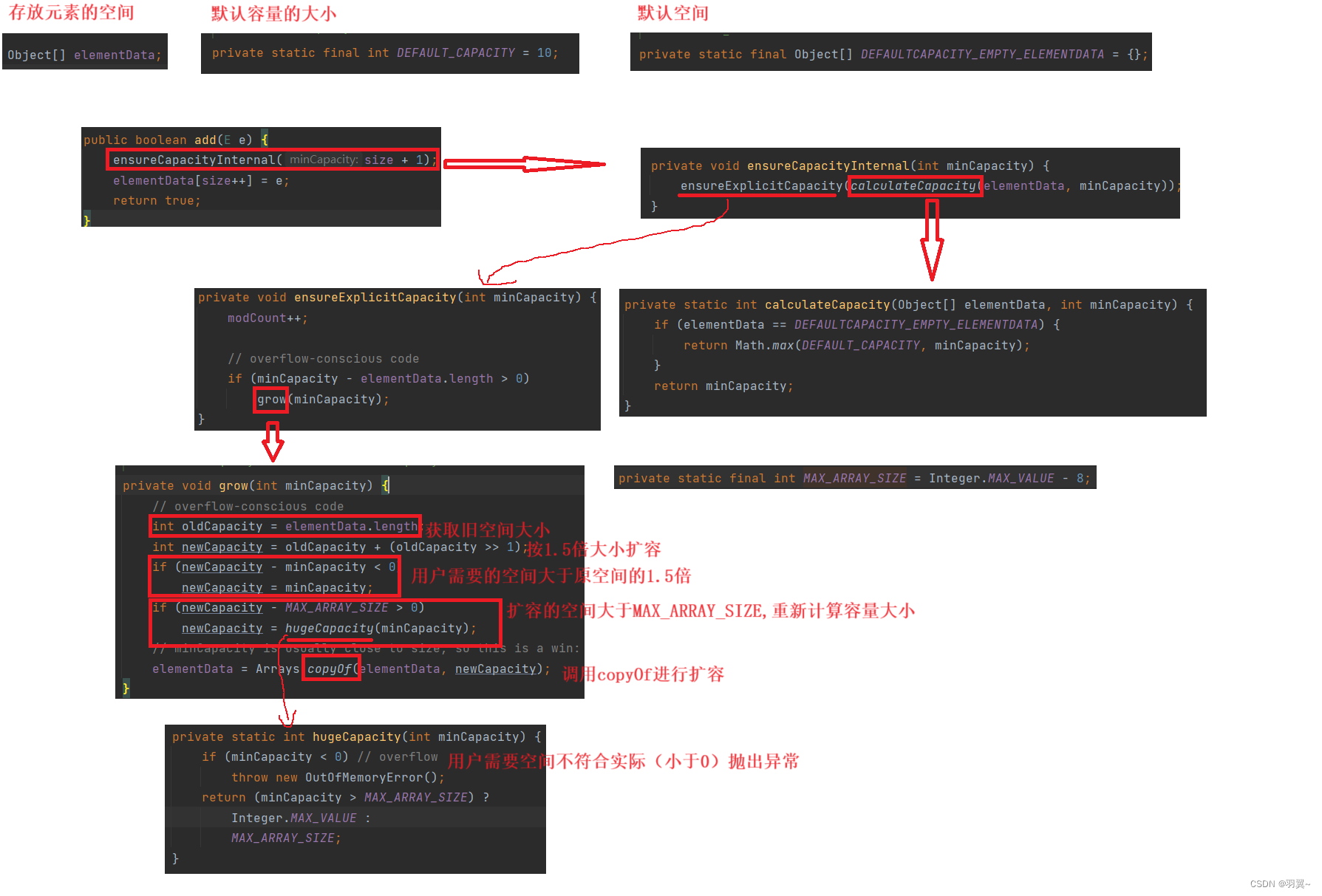
目录 一、List及其使用 1.1 List的概念 1.2 常见接口的介绍 1.3 List的使用 二、线性表和顺序表 2.1 线性表 2.2 顺序表 三、ArrayList介绍 四、ArrayList的使用 4.1 ArrayList构造 4.2 ArrayList的常用方法 4.3 ArrayList的遍历 4.4 ArrayList的扩容机制 五、ArrayList的具…...
【C++】特殊类的设计
文章目录 1. 设计一个类, 不能被拷贝2. 设计一个类, 不能被继承3. 设计一个类, 只能在堆上创建对象3. 设计一个类, 只能在栈上创建对象4. 创建一个类, 只能创建一个对象(单例模式)饿汉模式懒汉模式 1. 设计一个类, 不能被拷贝 💕 C98方式: 在C11之前&a…...
机器学习:PCA(Principal Component Analysis主成分)降维
参考:PCA降维原理 操作步骤与优缺点_TranSad的博客-CSDN博客 PCA降维算法_偶尔努力翻身的咸鱼的博客-CSDN博客 需要提前了解的数学知识: 一、PCA的主要思想 PCA,即主成分分析方法,是一种使用最广泛的数据降维算法。PCA的主要思想…...

linux服务器slab缓存回收方案设计
背景 自己写的回收slab内存ko,insmod报错“shrink_slab:unknown symbol _x86_indirect_thunk_rax(err 0)””; 分析 1.名词解释 在 x86 架构中,函数调用通常使用 call 指令来直接跳转到目标函数的地址。但是,当需要通过函数指针或动态链接调用函数时,就需要使用__x86_…...

Apache Spark 的基本概念
Apache Spark 是一种快速、可扩展、通用的数据处理引擎。它是一种基于内存的计算框架,支持分布式数据处理、机器学习、图形计算等多种计算任务。与传统的 Hadoop MapReduce 相比,Spark 具有更高的性能和更广泛的应用场景。 Spark 中的基本概念包括&…...
通讯协议介绍CoAP 协议解析
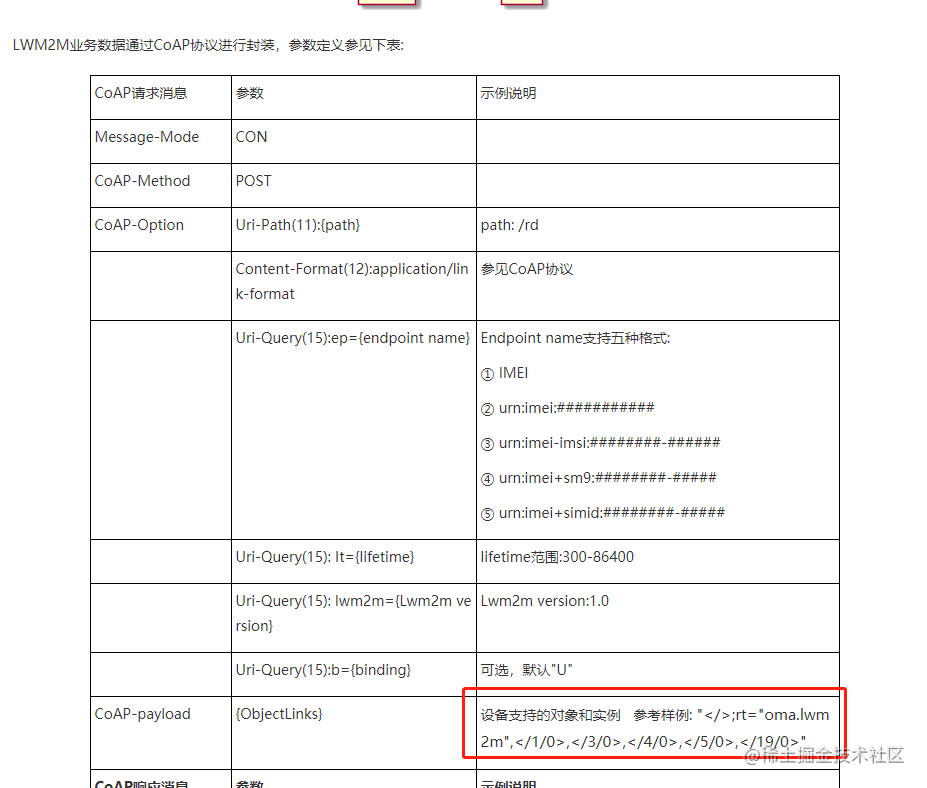
目录 1 通讯协议 2 TCP/IP 网络模型 2.1 TCP协议 2.1.1 TCP 连接过程 2.1.2 TCP 断开连接 2.1.3 TCP协议特点 2.2 UDP协议 2.2.1 UDP 协议特点 3 应用层协议简介 3.1 HTTP 协议 3.2 CoAP 协议 3.3 MQTT 协议 4 CoAP 协议详解 4.1 REST 风格 4.2 CoAP 首部分析 4…...
React 开发一个移动端项目(2)
配置基础路由 目标:配置登录页面的路由并显示在页面中 步骤: 安装路由: yarn add react-router-dom5.3.0 5 和 6 两个版本对组件类型的兼容性和函数组件支持有所改变,在这里使用的是 5。 和路由的类型声明文件 yarn add types…...

51单片机 点阵矩阵 坤坤代码
真正的黑子 #include <REGX52.H>void Delay(unsigned int xms); void _74HC595_WriteByte(unsigned char byte); void LED(unsigned char Y,DATA); void LED_Init();sbit RCKP3^5; //RCLK sbit SCKP3^6; //SRCL sbit SERP3^4; //SER //坤坤矩阵 unsigned char code D…...

Android13-图片视频选择器
在compileSDK 33 时,谷歌在安卓新增了 图片选择器 功能,支持单选、多选、选图片、视频等操作,并且不需要额外获取照片/音频权限。 具体实现如下: 1:请求 Log.d(TAG, "Build.VERSION.SDK_INT" Build.VERS…...
【问题处理】GIT合并解决冲突后,导致其他人代码遗失的排查
GIT合并解决冲突后,导致其他人代码遗失的排查 项目场景问题描述分析与处理:1. 警告分析2. 文件分析3. 问题关键4. 验证 解决策略总结 📕作者简介:战斧,从事金融IT行业,有着多年一线开发、架构经验ÿ…...
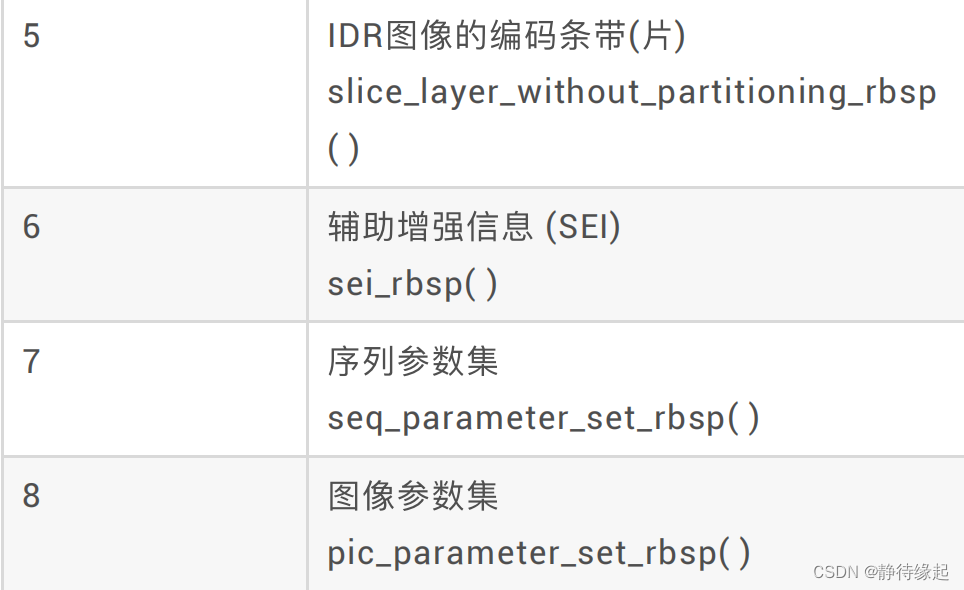
H264视频压缩格式
H264简介 H.264从1999年开始,到2003年形成草案,最后在2007年定稿有待核实。在ITU的标准里称为H.264, 在MPEG的标准里是MPEG-4的一个组成部分-MPEG-4 Part 10,又叫Advanced Video Codec,因此常常称为MPEG-4AVC或直接叫AVC。 压缩算…...

动态的中秋爱心演示送女友用python生成爱心软件文末附c++语言写法
用python生成爱心软件 用python生成动态爱心软件 目录 用python生成爱心软件 完整代码 代码解释 逐句解释 效果展示: 如何打包 c写法 完整代码 import turtledef draw_heart():love turtle.Turtle()love.getscreen().bgcolor("black")love.…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
