【力扣周赛】第 362 场周赛(⭐差分匹配状态压缩DP矩阵快速幂优化DPKMP)
文章目录
- 竞赛链接
- Q1:2848. 与车相交的点
- 解法1——排序后枚举
- 解法2——差分数组⭐
- 差分数组相关题目列表📕
- 1094. 拼车
- 1109. 航班预订统计
- 2381. 字母移位 II
- 2406. 将区间分为最少组数
- 解法1——排序贪心+优先队列
- 解法2——差分数组
- 2772. 使数组中的所有元素都等于零
- 2528. 最大化城市的最小供电站数目(⭐差分数组 + 二分查找答案)
- 最大化最小化相关题目列表📕
- Q2:2849. 判断能否在给定时间到达单元格(脑筋急转弯、贪心)
- Q3:2850. 将石头分散到网格图的最少移动次数⭐⭐⭐(全排列和状态压缩)
- 解法1——枚举全排列
- 解法2——最小费用最大流 (TODO)
- 解法3——状压DP
- 涉及到「匹配」的题目列表📕
- 1947. 最大兼容性评分和
- 解法1——枚举全排列
- 解法2——状态压缩DP
- 1349. 参加考试的最大学生数🚹(状态压缩DP)
- LCP 04. 覆盖🚹(TODO 二分图匹配 & 状态压缩DP)
- 解法1——二分图匹配
- 解法2——状态压缩DP
- 1879. 两个数组最小的异或值之和(状态压缩DP)
- 2172. 数组的最大与和(状态压缩DP)
- Q4:2851. 字符串转换⭐
- 解法1——KMP + 矩阵快速幂优化 DP 🐂
- 解法2——找规律,无需矩阵快速幂(TODO)
- [矩阵快速幂] 题目列表📕
- 成绩记录
竞赛链接
https://leetcode.cn/contest/weekly-contest-362/
Q1:2848. 与车相交的点
https://leetcode.cn/problems/points-that-intersect-with-cars/description/

提示:
1 <= nums.length <= 100
nums[i].length == 2
1 <= starti <= endi <= 100
解法1——排序后枚举
排序之后按顺序枚举,每次比较和上个区间结束位置之间的关系。
class Solution {public int numberOfPoints(List<List<Integer>> nums) {int ans = 0, last = -1;Collections.sort(nums, (x, y) -> x.get(0) - y.get(0));for (List<Integer> x: nums) {ans += Math.max(0, x.get(1) - Math.max(last + 1, x.get(0)) + 1);last = Math.max(last, x.get(1));}return ans;}
}
解法2——差分数组⭐
https://leetcode.cn/problems/points-that-intersect-with-cars/solutions/2435384/chai-fen-shu-zu-xian-xing-zuo-fa-by-endl-3xpm/
关于差分可见:【算法基础】1.5 前缀和与差分
class Solution {public int numberOfPoints(List<List<Integer>> nums) {int[] diff = new int[102];// 利用差分将区间内所有位置 +1for (List<Integer> p: nums) {diff[p.get(0)]++;diff[p.get(1) + 1]--;}int ans = 0, s = 0;// 检查各个位置 如果>0则ans++for (int d: diff) {s += d;if (s > 0) ans++;}return ans;}
}
差分数组相关题目列表📕
题目列表来源:分享|【算法小课堂】差分数组(Python/Java/C++/Go/JS)
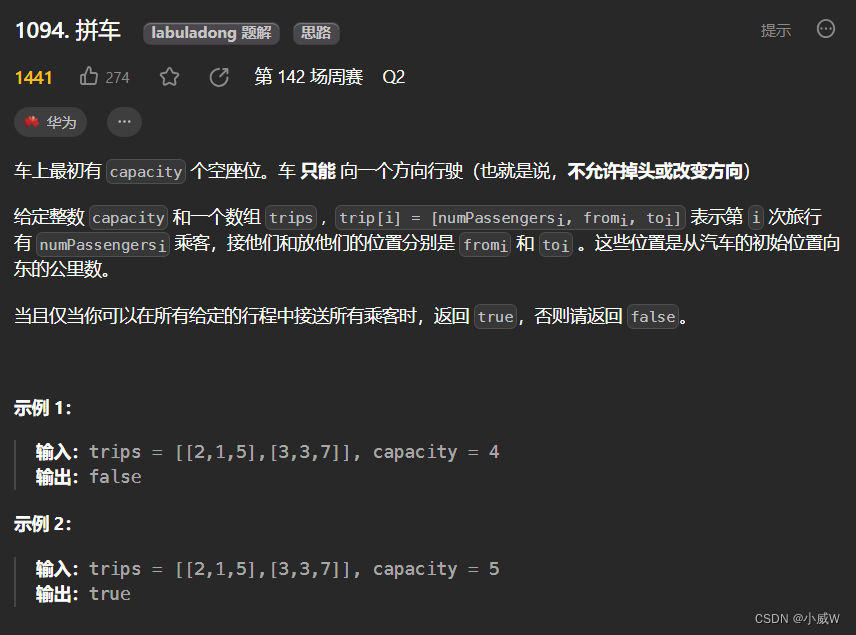
1094. 拼车
https://leetcode.cn/problems/car-pooling/
提示:
1 <= trips.length <= 1000
trips[i].length == 3
1 <= numPassengersi <= 100
0 <= fromi < toi <= 1000
1 <= capacity <= 10^5
用差分 表示 from 到 to 的范围内增加了多少人,然后再还原。
class Solution {public boolean carPooling(int[][] trips, int capacity) {int[] diff = new int[1002];// 构造差分数组for (int[] t: trips) {diff[t[1]] += t[0];diff[t[2]] -= t[0];}// 差分数组的还原for (int i = 0; i <= 1000; ++i) {if (diff[i] > capacity) return false;diff[i + 1] += diff[i];}return true;}
}
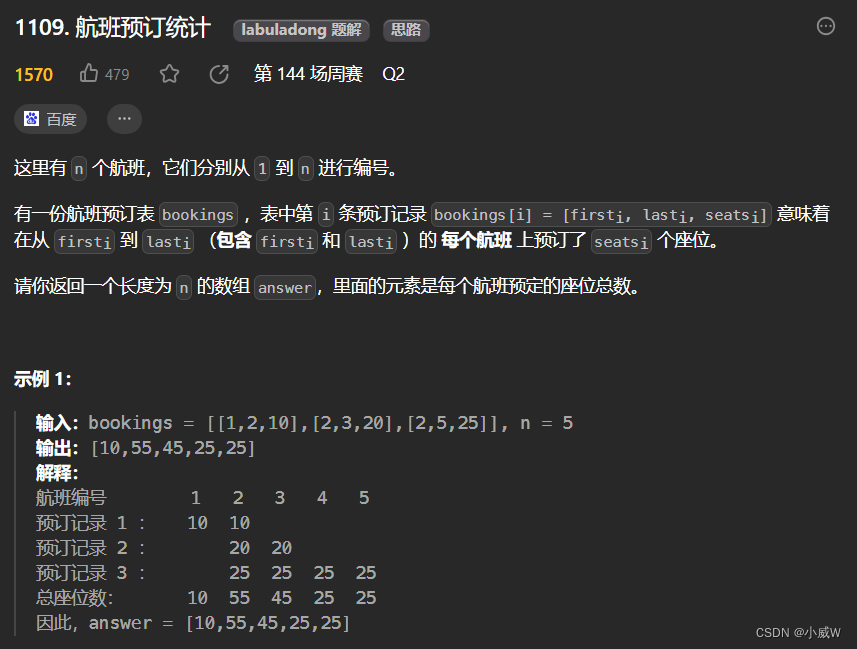
1109. 航班预订统计
https://leetcode.cn/problems/corporate-flight-bookings/
提示
1 <= n <= 2 * 10^4
1 <= bookings.length <= 2 * 10^4
bookings[i].length == 3
1 <= firsti <= lasti <= n
1 <= seatsi <= 10^4
class Solution {public int[] corpFlightBookings(int[][] bookings, int n) {int[] ans = new int[n], diff = new int[n + 1];for (int[] booking: bookings) {diff[booking[0] - 1] += booking[2];diff[booking[1]] -= booking[2];}for (int i = 0; i < n; ++i) {ans[i] = diff[i];diff[i + 1] += diff[i];}return ans;}
}
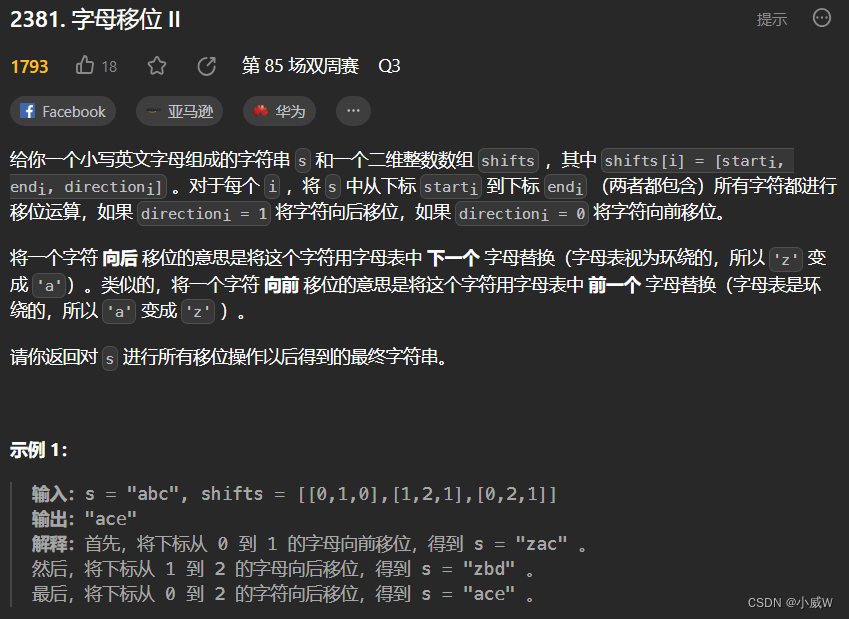
2381. 字母移位 II
https://leetcode.cn/problems/shifting-letters-ii/
提示
1 <= s.length, shifts.length <= 5 * 10^4
shifts[i].length == 3
0 <= starti <= endi < s.length
0 <= directioni <= 1
s 只包含小写英文字母。
class Solution {public String shiftingLetters(String s, int[][] shifts) {int n = s.length();// 构造差分数组int[] diff = new int[n + 1];for (int[] shift: shifts) {int t = shift[2] == 1? 1: -1;diff[shift[0]] += t;diff[shift[1] + 1] -= t;}// 差分数组和答案的还原char[] ans = new char[n];for (int i = 0; i < n; ++i) {ans[i] = op(s.charAt(i), diff[i]);diff[i + 1] += diff[i];}return String.valueOf(ans);}// 对字符 a 移动 xpublic char op(char a, int x) {return (char)(((a - 'a' + x % 26) + 26) % 26 + 'a');}
}
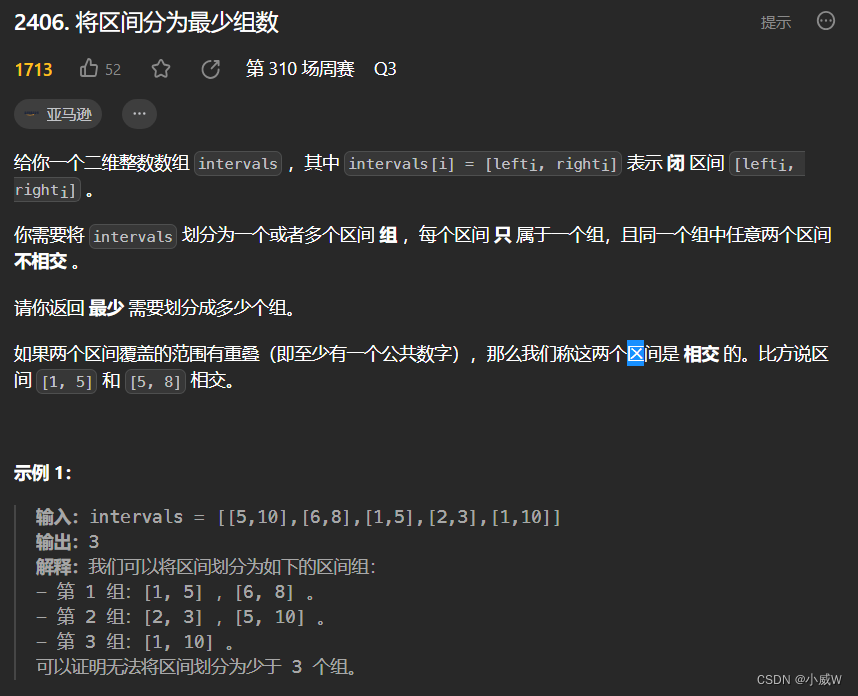
2406. 将区间分为最少组数
https://leetcode.cn/problems/divide-intervals-into-minimum-number-of-groups/
提示:
1 <= intervals.length <= 1^05
intervals[i].length == 2
1 <= lefti <= righti <= 10^6
解法1——排序贪心+优先队列
按照区间的开始位置从小到大排序。
想象每个组合就是一个列表,我们使用有限队列维护这些列表的末尾位置。
这样每次枚举到一个新的区间,检查是否可以放入已有列表中,如果可以,就将一个已有列表的末尾位置换成当前区间的结尾位置。
class Solution {public int minGroups(int[][] intervals) {Arrays.sort(intervals, (x, y) -> x[0] - y[0]);PriorityQueue<Integer> pq = new PriorityQueue<>((x, y) -> x - y);for (int[] interval: intervals) {if (!pq.isEmpty() && pq.peek() < interval[0]) pq.poll();pq.offer(interval[1]);}return pq.size();}
}
解法2——差分数组
差分还原中出现的最大值就是答案。
class Solution {public int minGroups(int[][] intervals) {TreeMap<Integer, Integer> diff = new TreeMap<>();int ans = 0, sum = 0;// 计算差分for (int[] interval: intervals) {diff.merge(interval[0], 1, Integer::sum);diff.merge(interval[1] + 1, -1, Integer::sum);}// 还原差分for (Map.Entry<Integer, Integer> entry: diff.entrySet()) {sum += entry.getValue();ans = Math.max(ans, sum);}return ans;}
}
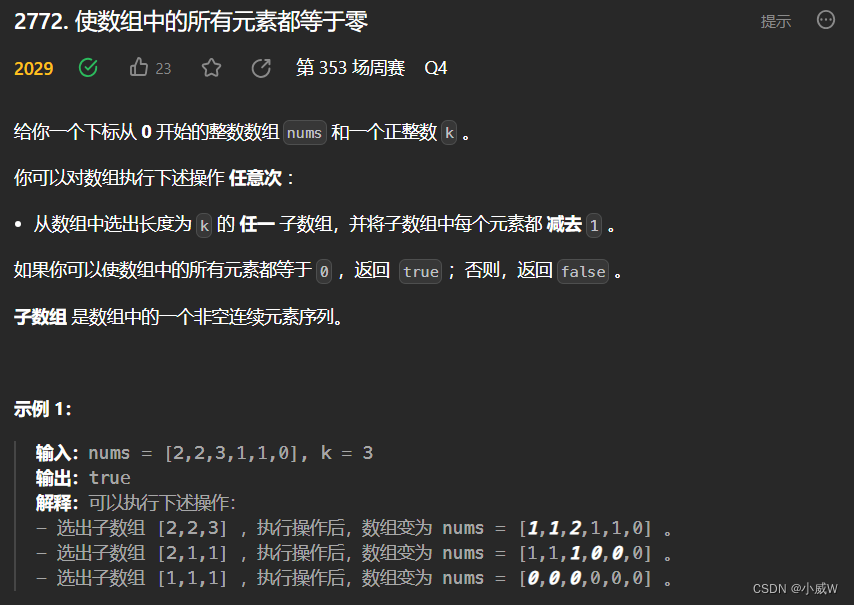
2772. 使数组中的所有元素都等于零
https://leetcode.cn/problems/apply-operations-to-make-all-array-elements-equal-to-zero/
提示:
1 <= k <= nums.length <= 10^5
0 <= nums[i] <= 10^6
有点差分的思想,又不太一样。
贪心地从前往后枚举每一个位置,只要 > 0 就减,< 0 就返回 false。
class Solution {public boolean checkArray(int[] nums, int k) {int n = nums.length, diff = 0, ans = 0;int[] x = new int[n];for (int i = 0; i < n; ++i) {if (i >= k) diff -= x[i - k];if (nums[i] > diff) {if (n - i < k) return false;ans += nums[i] - diff; // 更新答案x[i] = nums[i] - diff; // 记录这个位置减去了多少diff = nums[i]; // 更新diff} else if (nums[i] < diff) return false;}return true;}
}
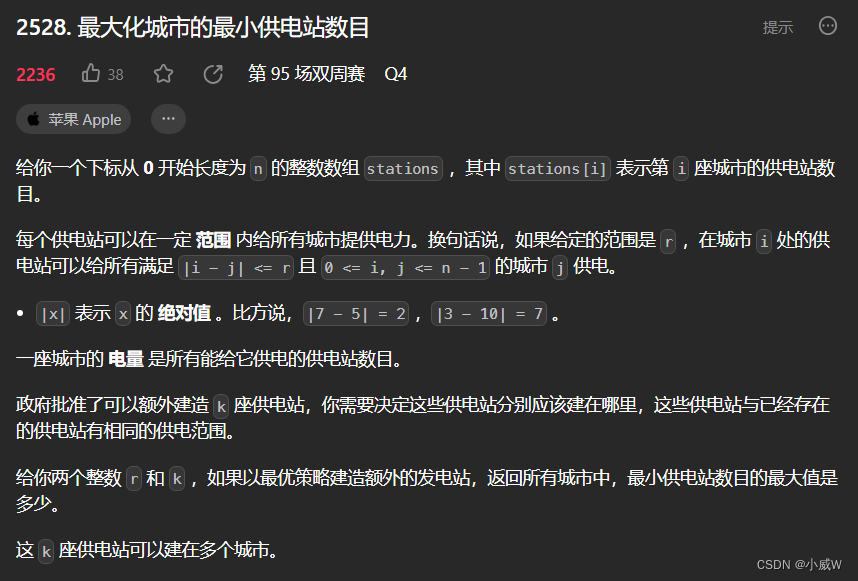
2528. 最大化城市的最小供电站数目(⭐差分数组 + 二分查找答案)
https://leetcode.cn/problems/maximize-the-minimum-powered-city/
提示:
n == stations.length
1 <= n <= 10^5
0 <= stations[i] <= 10^5
0 <= r <= n - 1
0 <= k <= 10^9
看到「最大化最小值」或者「最小化最大值」就要想到二分答案,这是一个固定的套路。
class Solution {public long maxPower(int[] stations, int r, int k) {int n = stations.length;long mn = Long.MAX_VALUE;// 计算差分数组long[] cnt = new long[n + 1];for (int i = 0; i < n; ++i) {cnt[Math.max(0, i - r)] += stations[i];cnt[Math.min(n, i + r + 1)] -= stations[i];}// 差分数组的还原for (int i = 0; i < n; ++i) {cnt[i + 1] += cnt[i];mn = Math.min(mn, cnt[i]);}// 二分查找答案long left = mn, right = mn + k;while (left < right) {long mid = left + right + 1 >> 1;if (!check(cnt, mid, r, k)) right = mid - 1;else left = mid;}return left;}// check过程类似 T2772. 使数组中的所有元素都等于零public boolean check(long[] cnt, long x, int r, int k) {long diff = 0;int n = cnt.length - 1;long[] d = new long[n];for (int i = 0; i < n; ++i) {if (i >= 2 * r + 1) diff -= d[i - 2 * r - 1];if (cnt[i] + diff < x) {d[i] = x - cnt[i] - diff;k -= d[i];diff = x - cnt[i];}}return k >= 0;}
}
最大化最小化相关题目列表📕
见:【算法】二分答案 对应部分。
Q2:2849. 判断能否在给定时间到达单元格(脑筋急转弯、贪心)
https://leetcode.cn/problems/determine-if-a-cell-is-reachable-at-a-given-time/

提示:
1 <= sx, sy, fx, fy <= 109
0 <= t <= 10^9
斜着走,一步顶两步——相当于可以同时横着走和竖着走。 那么只要满足垂直和水平方向中最长的那个距离就好了。
注意有个特例是:只走一步时,如果起点和终点相同就不可以了。
class Solution {public boolean isReachableAtTime(int sx, int sy, int fx, int fy, int t) {if (sx == fx && sy == fy && t == 1) return false; // 特例return t >= Math.max(Math.abs(sx - fx), Math.abs(sy - fy));}
}
Q3:2850. 将石头分散到网格图的最少移动次数⭐⭐⭐(全排列和状态压缩)
https://leetcode.cn/problems/minimum-moves-to-spread-stones-over-grid/

提示:
grid.length == grid[i].length == 3
0 <= grid[i][j] <= 9
grid 中元素之和为 9
解法1——枚举全排列
https://leetcode.cn/problems/minimum-moves-to-spread-stones-over-grid/solutions/2435313/tong-yong-zuo-fa-zui-xiao-fei-yong-zui-d-iuw8/
将起始点和终点分别放入两个列表,做全排列匹配。
枚举所有全排列,比较各种情况下的移动次数,得出最小移动次数。
class Solution {int ans = Integer.MAX_VALUE, sum = 0;boolean[] st = new boolean[9];public int minimumMoves(int[][] grid) {// 将起始点和终点放入列表List<int[]> src = new ArrayList<>(), dst = new ArrayList<>();for (int i = 0; i < 3; ++i) {for (int j = 0; j < 3; ++j) {while (grid[i][j] > 1) {src.add(new int[]{i, j});grid[i][j]--;}if (grid[i][j] == 0) dst.add(new int[]{i, j});}}// dfs全排列dfs(0, src, dst);return ans;}public void dfs(int i, List<int[]> src, List<int[]> dst) {if (i == src.size()) {ans = Math.min(ans, sum);return;}for (int j = 0; j < dst.size(); ++j) {if (!st[j]) {int[] s = src.get(i), d = dst.get(j);sum += Math.abs(s[0] - d[0]) + Math.abs(s[1] - d[1]);st[j] = true;dfs(i + 1, src, dst);sum -= Math.abs(s[0] - d[0]) + Math.abs(s[1] - d[1]);st[j] = false;}}}
}
解法2——最小费用最大流 (TODO)
https://leetcode.cn/problems/minimum-moves-to-spread-stones-over-grid/solutions/2435313/tong-yong-zuo-fa-zui-xiao-fei-yong-zui-d-iuw8/
在这里插入代码片
解法3——状压DP
https://leetcode.cn/problems/minimum-moves-to-spread-stones-over-grid/solutions/2435319/zhuang-ya-dp-by-tsreaper-jiw0/
状态压缩DP相比全排列速度更快(48ms vs 3ms)
class Solution {public int minimumMoves(int[][] grid) {// 起始点和目的点放入两个列表List<int[]> L = new ArrayList<>(), R = new ArrayList<>();for (int i = 0; i < 3; ++i) {for (int j = 0; j < 3; ++j) {if (grid[i][j] == 0) R.add(new int[]{i, j});else {for (; grid[i][j] > 1; grid[i][j]--) {L.add(new int[]{i, j});}}}}// 状态压缩DPint n = L.size();int[] dp = new int[1 << n];Arrays.fill(dp, Integer.MAX_VALUE);dp[0] = 0;for (int i = 1; i < (1<<n); ++i) {// 计算 i 中有几个二进制等于 1——为了确定当前目的点是哪个int cnt = 0;for (int j = 0; j < n; ++j) {cnt += i >> j & 1;}// 状态转移for (int j = 0; j < n; ++j) { // 枚举所有目标点if ((i >> j & 1) == 1) { // 检查是否为1,即是否可以从前面转移过来dp[i] = Math.min(dp[i], dp[i ^ (1 << j)] + cost(R.get(cnt - 1), L.get(j)));}}}return dp[(1<<n) - 1];}public int cost(int[] a, int[] b) {return Math.abs(a[0] - b[0]) + Math.abs(a[1] - b[1]);}
}
涉及到「匹配」的题目列表📕
题单来源:https://leetcode.cn/problems/minimum-moves-to-spread-stones-over-grid/solutions/2435313/tong-yong-zuo-fa-zui-xiao-fei-yong-zui-d-iuw8/
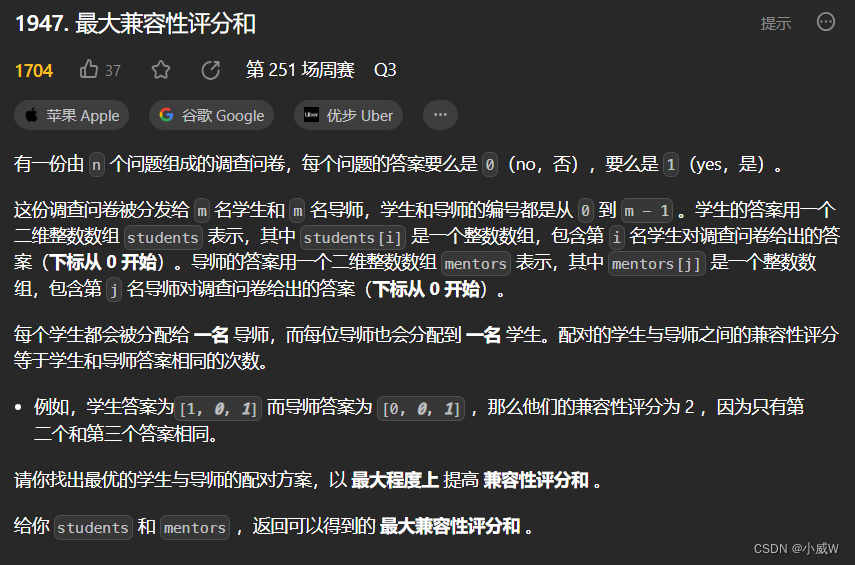
1947. 最大兼容性评分和
https://leetcode.cn/problems/maximum-compatibility-score-sum/
提示:
m == students.length == mentors.length
n == students[i].length == mentors[j].length
1 <= m, n <= 8
students[i][k] 为 0 或 1
mentors[j][k] 为 0 或 1
解法1——枚举全排列
数据范围很小,可以枚举出所有学生和老师之间匹配的方案。
class Solution {int ans = 0;boolean[] st = new boolean[8];public int maxCompatibilitySum(int[][] students, int[][] mentors) {// 全排列dfs(students, mentors, 0, 0);return ans;}public void dfs(int[][] students, int[][] mentors, int i, int sum) {if (i == students.length) {ans = Math.max(ans, sum);return;}for (int j = 0; j < mentors.length; ++j) {if (st[j]) continue;st[j] = true;dfs(students, mentors, i + 1, sum + cp(students[i], mentors[j]));st[j] = false;}}// 计算某个学生和某个老师的兼容性评分public int cp(int[] s, int[] t) {int res = 0;for (int i = 0; i < s.length; ++i) {if (s[i] == t[i]) res++;}return res;}
}
解法2——状态压缩DP
class Solution {public int maxCompatibilitySum(int[][] students, int[][] mentors) {int n = students.length;int[][] dp = new int[n + 1][1<<n]; // dp[i][j]表示匹配完i个老师,和集合j的学生的最大匹配和// 枚举每个状态for (int i = 1; i < (1<<n); ++i) {int idx = Integer.bitCount(i); // 计算该匹配哪个老师了// 枚举每个学生for (int j = 0; j < n; ++j) {if ((i >> j & 1) == 1) { // 如果可以转移dp[idx][i] = Math.max(dp[idx][i], dp[idx - 1][i ^ (1<<j)] + cp(students[j], mentors[idx - 1]));}}}return dp[n][(1<<n) - 1];}// 计算某个学生和某个老师的兼容性评分public int cp(int[] s, int[] t) {int res = 0;for (int i = 0; i < s.length; ++i) {if (s[i] == t[i]) res++;}return res;}
}
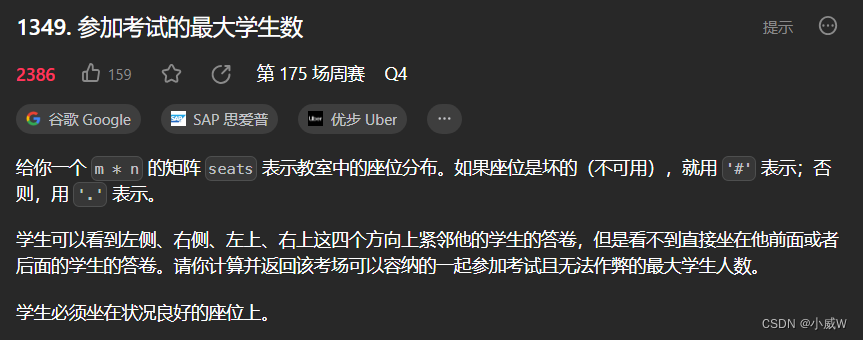
1349. 参加考试的最大学生数🚹(状态压缩DP)
https://leetcode.cn/problems/maximum-students-taking-exam/
提示:
seats 只包含字符 '.' 和'#'
m == seats.length
n == seats[i].length
1 <= m <= 8
1 <= n <= 8
将每一行选择的位置用一个int变量表示。
枚举每一行,再枚举该行的状态,然后枚举上一行的状态,检测是否合理且可以转移过来。
最后的答案就是最后一行各个状态的最大值。
这里的合理包括:
- 该行本身要合理,—— 都要坐在正常的椅子上;同一行的两个学生不能挨边坐。
- 每一行和上一行之间不能有冲突——如果上一行的某一列已经坐人了,那么该行该列的左右两侧就不能坐人了。
class Solution {public int maxStudents(char[][] seats) {int m = seats.length, n = seats[0].length;int[] states = new int[m];for (int i = 0; i < m; ++i) {states[i] = getMask(seats[i]);}// 一共m行,每行1<<n种状态int[][] dp = new int[m + 1][1 << n];for (int i = 0; i < 1<<n; ++i) {// 判断 i 是不是 states[0] 的子集 && 自己不冲突if (check(states[0], i) && op(i)) {dp[0][i] = Integer.bitCount(i);}}// 枚举每一行for (int i = 1; i < m; ++i) {// 枚举这一行的每个状态for (int j = 0; j < 1<<n; ++j) {if (!check(states[i], j)) continue; // 如果这个状态不合理,就跳过// 枚举上一行的每个状态for (int k = 0; k < 1<<n; ++k) {if (!check(states[i - 1], k)) continue; // 如果这个状态不合理,就跳过if (!confilt(k, j)) { // 如果这个状态和上一行不冲突dp[i][j] = Math.max(dp[i][j], dp[i - 1][k] + Integer.bitCount(j));}}}System.out.println();}return Arrays.stream(dp[m - 1]).max().getAsInt();}// 将一行的状态用一个int表示public int getMask(char[] state) {int res = 0;for (int i = 0; i < state.length; ++i) {if (state[i] == '.') res |= 1 << i;}return res;}// 检查状态x是否是状态state的子集,即是否可选 && 这个状态x本身合法public boolean check(int state, int x) {if ((state | x) != state) return false; // 需要x是state的子集return op(x); }// 检查x是否和y作为上一行冲突public boolean confilt(int x, int y) {for (int i = 0; i < 10; ++i) {if ((x >> i & 1) == 1) { // 如果x这个位置有了// 那么y的相差一列的位置就不能有了if ((y >> i + 1 & 1) == 1 || (y >> i - 1 & 1) == 1) {return true;}}}return false;}// 检查这一行的状态本身是否合理,即检查是否有两个学生坐在挨边的位置上public boolean op(int x) {for (int i = 0; i < 9; ++i) {if ((x >> i & 1) == 1 && (x >> i + 1 & 1) == 1) return false;}return true;}
}
LCP 04. 覆盖🚹(TODO 二分图匹配 & 状态压缩DP)
https://leetcode.cn/problems/broken-board-dominoes/
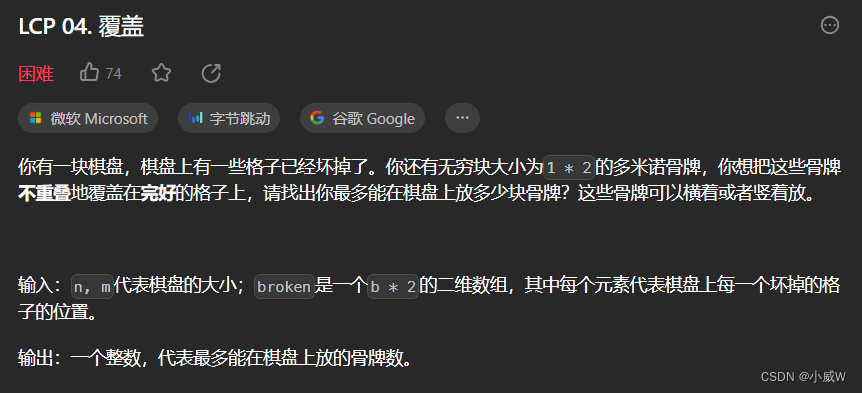
限制:
1 <= n <= 8
1 <= m <= 8
0 <= b <= n * m
解法1——二分图匹配
在这里插入代码片
解法2——状态压缩DP
在这里插入代码片
1879. 两个数组最小的异或值之和(状态压缩DP)
https://leetcode.cn/problems/minimum-xor-sum-of-two-arrays/
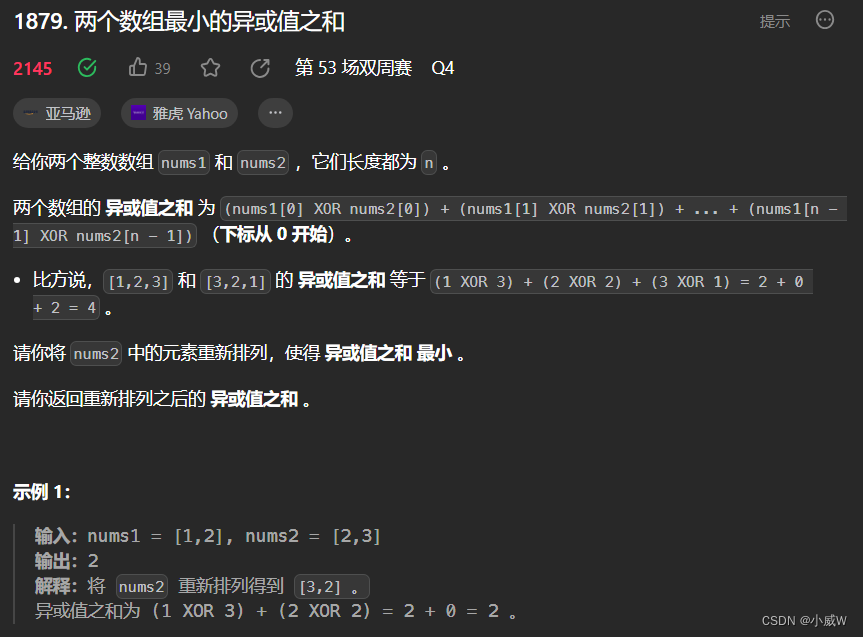
提示:
n == nums1.length
n == nums2.length
1 <= n <= 14
0 <= nums1[i], nums2[i] <= 10^7
class Solution {public int minimumXORSum(int[] nums1, int[] nums2) {int n = nums1.length;int[][] dp = new int[n + 1][1 << n];for (int i = 0; i <= n; ++i) Arrays.fill(dp[i], Integer.MAX_VALUE / 2);dp[0][0] = 0;// 枚举nums1的每个状态for (int i = 1; i < 1<<n; ++i) {int cnt = Integer.bitCount(i);// 枚举每个位置for (int j = 0; j < n; ++j) {if ((i >> j & 1) == 1) {dp[cnt][i] = Math.min(dp[cnt][i], dp[cnt - 1][i ^ (1<<j)] + (nums1[j] ^ nums2[cnt - 1]));}}}return dp[n][(1<<n) - 1];}
}
2172. 数组的最大与和(状态压缩DP)
https://leetcode.cn/problems/maximum-and-sum-of-array/
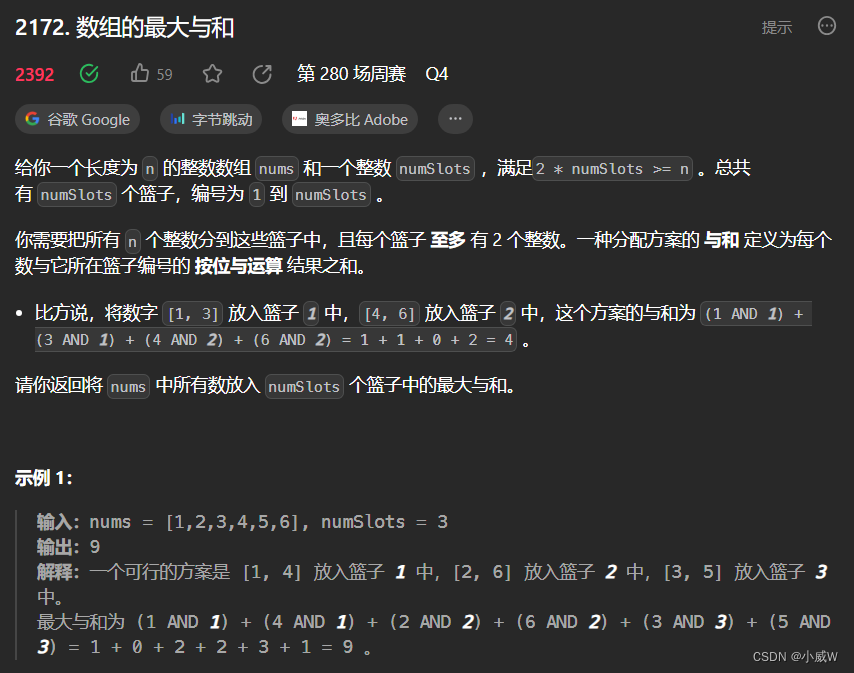
提示:
n == nums.length
1 <= numSlots <= 9
1 <= n <= 2 * numSlots
1 <= nums[i] <= 15
每个篮子可以放最多 2 个数字,那么可以分成有 2 组一模一样的篮子处理。
注意——要将篮子的使用集合作为状态。
class Solution {public int maximumANDSum(int[] nums, int numSlots) {int n = nums.length, m = 2 * numSlots, ans = 0;int[] dp = new int[1<<m]; // m个篮子的状态// 枚举每个篮子被选择情况for (int i = 1; i < 1<<m; ++i) {// 计算该放入那个num了int cnt = Integer.bitCount(i);if (cnt > n) continue;// 枚举每个被选择的篮子for (int j = 0; j < m; ++j) {if ((i >> j & 1) == 1) {dp[i] = Math.max(dp[i], dp[i ^ (1<<j)] + (nums[cnt - 1] & (j % numSlots + 1)));}}ans = Math.max(ans, dp[i]);}return ans;}
}
Q4:2851. 字符串转换⭐
https://leetcode.cn/problems/string-transformation/
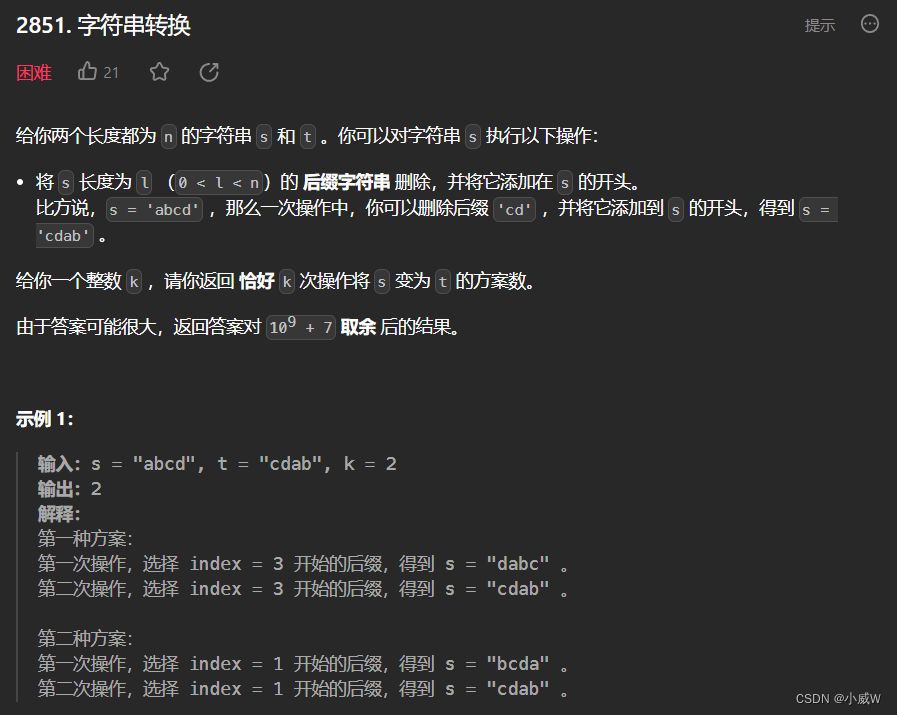
提示:
2 <= s.length <= 5 * 10^5
1 <= k <= 10^15
s.length == t.length
s 和 t 都只包含小写英文字母。
解法1——KMP + 矩阵快速幂优化 DP 🐂
https://leetcode.cn/problems/string-transformation/solutions/2435348/kmp-ju-zhen-kuai-su-mi-you-hua-dp-by-end-vypf/
计算有多少个 s 的循环同构字符串等于 t,记作 c。这可以用 KMP 等字符串匹配算法解决,即寻找 t 在 s+s(去掉最后一个字符)中的出现次数。(用KMP计算出 s + s 中有几个 t)
关于 KMP 可见:我一定要 学会KMP字符串匹配
下面使用动态规划来解决该问题——
定义 f[i][0] 表示 i 次操作后等于 t 的方案数,f[i][1] 表示 i 次操作后不等于 t 的方案数。

发现 DP 递推式可以写成矩阵乘法形式,因此可以使用矩阵快速幂来优化。(所谓矩阵快速幂,和普通快速幂的思想是一样的。)

快速幂可以完成从 O ( n ) O(n) O(n) 到 O ( log n ) O(\log{n}) O(logn) 的优化。
Q:为什么必须要使用矩阵快速幂?
A:因为 k 的数据范围很大。( log n \log{n} logn 对应的数据范围是 1 0 18 10^{18} 1018)
class Solution {final long MOD = (long)1e9 + 7;public int numberOfWays(String s, String t, long k) {int n = s.length();// kmp 求出 s+s(去掉最后一个字符) 中有几个 tint c = kmpSearch(s + s.substring(0, n - 1), t);// 递推矩阵long[][] m = {{c - 1, c},{n - c, n - 1 - c},};m = pow(m, k); // 矩阵快速幂求结果// 根据 s==t? 判断初始状态 对应的答案return s.equals(t)? (int) m[0][0]: (int) m[0][1];}// kmp 返回 s 中有多少个 tpublic int kmpSearch(String s, String t) {int[] next = getNext(s.toCharArray());int c = 0;for (int i = 0, j = -1; i < s.length(); ++i) {while (j != -1 && s.charAt(i) != t.charAt(j + 1)) j = next[j];if (s.charAt(i) == t.charAt(j + 1)) j++;if (j == t.length() - 1) {c++;j = next[j]; // 匹配成功之后,记得要更新 j = next[j]}}return c;}// 求 next 数组public int[] getNext(char[] s) {int n = s.length;int[] next = new int[n];next[0] = -1;for (int i = 1, j = -1; i < n; ++i) {while (j != -1 && s[i] != s[j + 1]) j = next[j];if (s[i] == s[j + 1]) j++;next[i] = j;}return next;}// 矩阵快速幂public long[][] pow(long[][] a, long n) {long[][] res = {{1, 0}, {0, 1}};for (; n > 0; n /= 2) {if (n % 2 == 1) {res = multiply(res, a);}a = multiply(a, a);}return res;}// 矩阵乘法public long[][] multiply(long[][] a, long[][] b) {long[][] c = new long[2][2];for (int i = 0; i < 2; ++i) {for (int j = 0; j < 2; ++j) {c[i][j] = (a[i][0] * b[0][j] + a[i][1] * b[1][j]) % MOD;}}return c;}
}
解法2——找规律,无需矩阵快速幂(TODO)
https://leetcode.cn/problems/string-transformation/solutions/2435714/cjavapython-bu-xu-yao-ju-zhen-kuai-su-mi-cukc/
在这里插入代码片
[矩阵快速幂] 题目列表📕
见:【算法】矩阵快速幂优化动态规划
成绩记录
本次没有参加竞赛。
相关文章:

【力扣周赛】第 362 场周赛(⭐差分匹配状态压缩DP矩阵快速幂优化DPKMP)
文章目录 竞赛链接Q1:2848. 与车相交的点解法1——排序后枚举解法2——差分数组⭐差分数组相关题目列表📕1094. 拼车1109. 航班预订统计2381. 字母移位 II2406. 将区间分为最少组数解法1——排序贪心优先队列解法2——差分数组 2772. 使数组中的所有元素…...
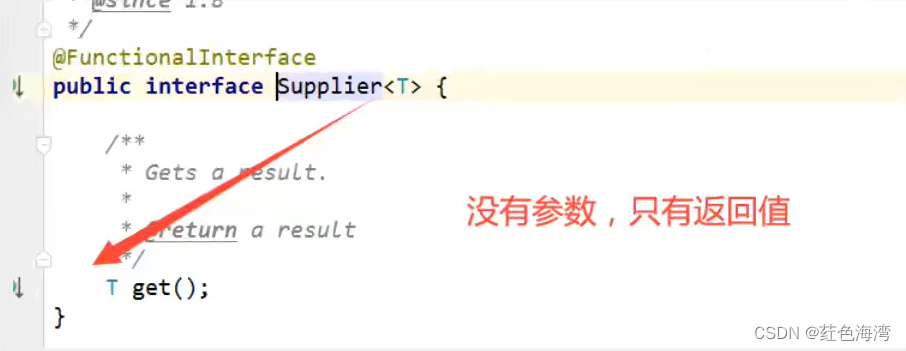
四大函数式接口(重点,必须掌握)
新时代程序员必须要会的 :lambda表达式、链式编程、函数式接口、Stream流式计算 什么是函数式接口 1.函数型接口 package com.kuang.function;import java.util.function.Function;/*** Function函数型接口 有一个输入参数,有一个输出* 只要是函数式接口…...
2023Web前端逻辑面试题
1、现有9个小球,已知其中一个球比其它的重,如何只用天平称2次就找出该球? ①把9个球分成三份,三个一份; ②拿出其中两份进行称量;会分为两种情况 若拿出的两份小球称量结果,重量相等;…...

uniapp中git忽略node_modules,unpackage文件
首先在当前项目的命令行新建.gitignore文件: touch .gitignore再在编辑器中打开该文件,并在该文件中加入需要忽略的文件名: node_modules/ .project unpackage/ .DS_Store 提示:如果以前提交过unpackage文件的话,需…...

Json-Jackson和FastJson
狂神: 测试Jackson 纯Java解决日期格式化 设置ObjectMapper FastJson: 知乎:Jackson使用指南 1、常见配置 方式一:yml配置 spring.jackson.date-format指定日期格式,比如yyyy-MM-dd HH:mm:ss,或者具体的…...

RK3588 点亮imx586摄像头
一.硬件原理图 mipi摄像头硬件确认点: 1.供电:5V,2.8V,1.2V,1.8V,reset脚(硬拉3.3,上电的时候从低到高),pwron脚外接 3.3V。 2,时钟:MCLKOUT是2…...
C++---继承
继承 前言继承的概念及定义继承的概念继承定义继承关系和访问限定符 基类和派生类对象赋值转换继承中的作用域派生类的默认成员函数继承与友元继承与静态成员**多重继承**多继承下的类作用域菱形继承虚继承使用虚基类 支持向基类的常规类型转换 前言 在需要写Father类和Mother…...

使用新版Maven-mvnd快速构建项目
目前我们项目的构建方式多数是 maven、gradle,但是 maven 相对 gradle 来说,构建速度较慢,特别是模块相对较多的时候,构建速度更加明显。但是我们将项目由 maven 替换为 gradle 相对来说会比较麻烦,成本较高。于是我们…...
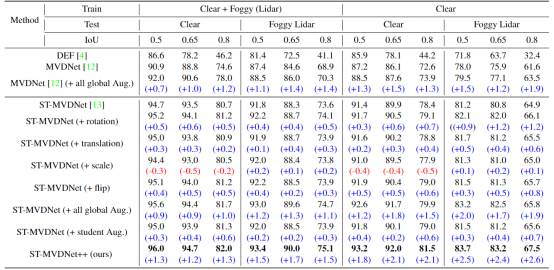
【ICASSP 2023】ST-MVDNET++论文阅读分析与总结
主要是数据增强的提点方式。并不能带来idea启发,但对模型性能有帮助 Challenge: 少有作品应用一些全局数据增强,利用ST-MVDNet自训练的师生框架,集成了更常见的数据增强,如全局旋转、平移、缩放和翻转。 Contributi…...
MySQL 面试题——MySQL 基础
目录 1.什么是 MySQL?有什么优点?2.MySQL 中的 DDL 与 DML 是分别指什么?3.✨数据类型 varchar 与 char 有什么区别?4.数据类型 BLOB 与 TEXT 有什么区别?5.DATETIME 和 TIMESTAMP 的异同?6.✨MySQL 中 IN …...
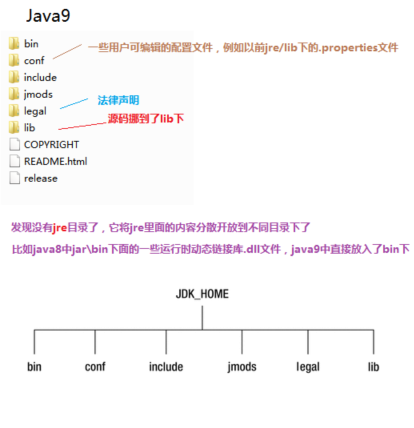
JDK9特性——概述
文章目录 引言JDK9特性概述JDK9的改变JDK和JRE目录变化总结 引言 JAVA8 及之前,版本都是特性驱动的版本更新,有重大的特性产生,然后进行更新。 JAVA9开始,JDK开始以时间为驱动进行更新,以半年为周期,到时…...

征战开发板从无到有(三)
接上一篇,翘首已盼的PCB板子做好了,管脚约束信息都在PCB板上体现出来了,很满意,会不会成为爆款呢,嘿嘿,来,先看看PCB裸板美图 由于征战开发板电路功能兼容小梅哥ACX720,大家可以直…...
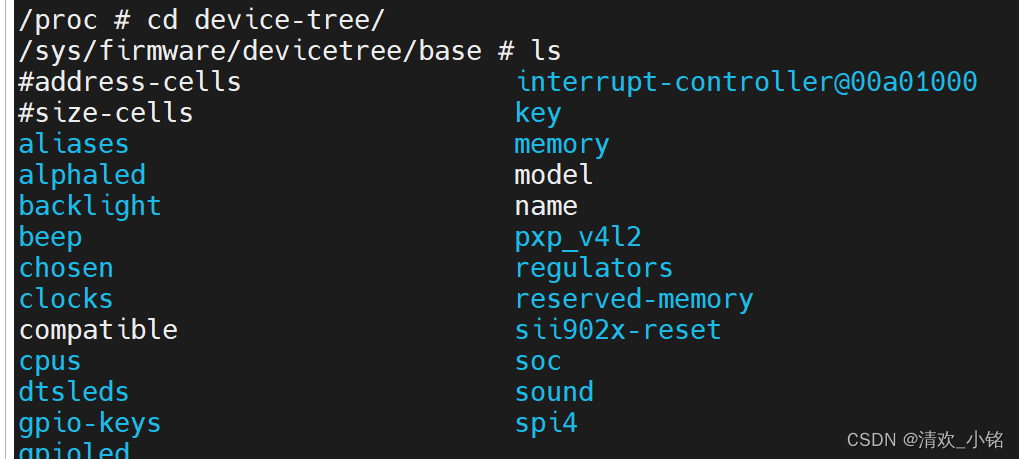
Linux设备树详细学习笔记
参考文献 参考视频 开发板及程序 原子mini 设备树官方文档 设备树的基本概念 DT:Device Tree //设备树 FDT: Flattened Device Tree //开放设备树,起源于OpenFirmware (所以后续会见到很多OF开头函数) dts: device tree source的缩写 //设备树源码 dtsi: device …...
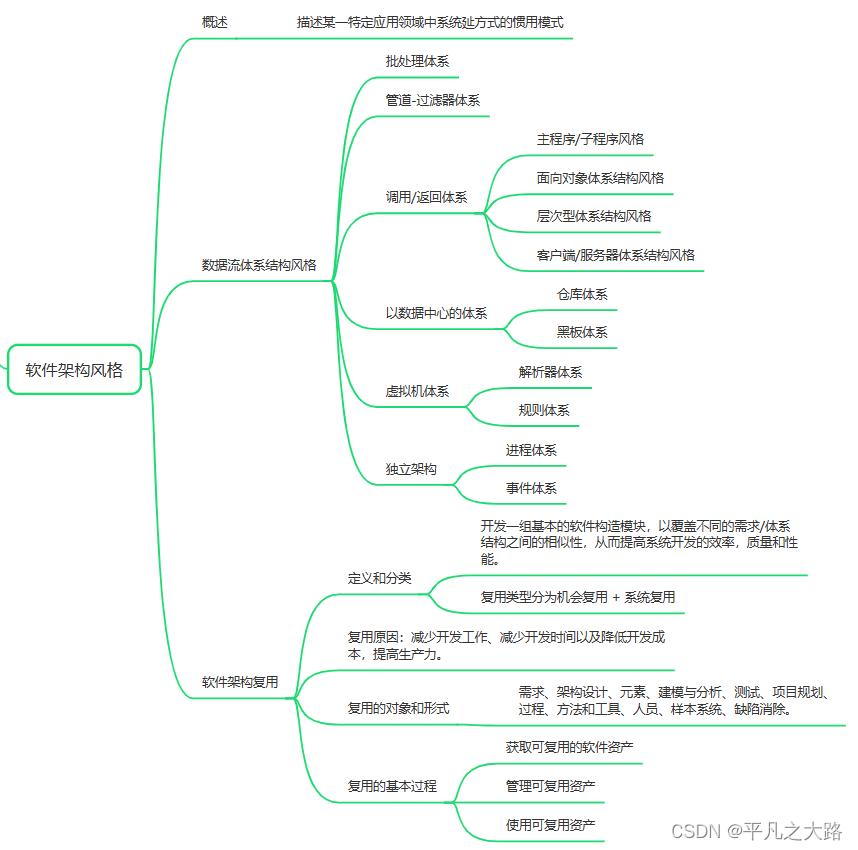
【系统架构】系统架构设计基础知识
导读:本文整理关于系统架构设计基础知识来构建系统架构知识体系。完整和扎实的系统架构知识体系是作为架构设计的理论支撑,基于大量项目实践经验基础上,不断加深理论体系的理解,从而能够创造新解决系统相关问题。 目录 1、软件架…...
快递、外卖、网购自动定位及模糊检索收/发件地址功能实现
概述 目前快递、外卖、团购、网购等行业 :为了简化用户在收发件地址填写时的体验感,使用辅助定位及模糊地址检索来丰富用户的体验 本次demo分享给大家;让大家理解辅助定位及模糊地址检索的功能实现过程,以及开发出自己理想的作品…...

Springboot后端导入导出excel表
一、依赖添加 操作手册:Hutool — 🍬A set of tools that keep Java sweet. <!--hutool工具包--><dependency><groupId>cn.hutool</groupId><artifactId>hutool-all</artifactId><version>5.7.20</versio…...
通过stream流实现分页、模糊搜索、按列过滤功能
通过stream实现分页、模糊搜索、按列过滤功能 背景逻辑展示示例代码 背景 在有一些数据通过数据库查询出来后,需要经过一定的逻辑处理才进行前端展示,这时候需要在程序中进行相应的分页、模糊搜索、按列过滤了。这些功能通过普通的逻辑处理可能较为繁琐…...

webpack:系统的了解webpack一些核心概念
文章目录 webpack 如何处理应用程序?何为webpack模块chunk?入口(entry)输出(output)loader开发loader 插件(plugin)简介流程插件开发:Tapable类监听(watching)compiler 钩子compilation 钩子compiler和compilation创建自定义 插件 loader和pl…...

Unreal Engine Loop 流程
引擎LOOP 虚幻引擎的启动是怎么一个过程。 之前在分析热更新和加载流程过程中,做了一个图。记录一下!! 
FLASK中的鉴权的插件Flask-HTTPAuth
在 Web 应用中,我们经常需要保护我们的 api,以避免非法访问。比如,只允许登录成功的用户发表评论等。Flask-HTTPAuth 扩展可以很好地对 HTTP 的请求进行认证,不依赖于 Cookie 和 Session。本文主要介绍两种认证的方式:…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...
C++11 constexpr和字面类型:从入门到精通
文章目录 引言一、constexpr的基本概念与使用1.1 constexpr的定义与作用1.2 constexpr变量1.3 constexpr函数1.4 constexpr在类构造函数中的应用1.5 constexpr的优势 二、字面类型的基本概念与使用2.1 字面类型的定义与作用2.2 字面类型的应用场景2.2.1 常量定义2.2.2 模板参数…...
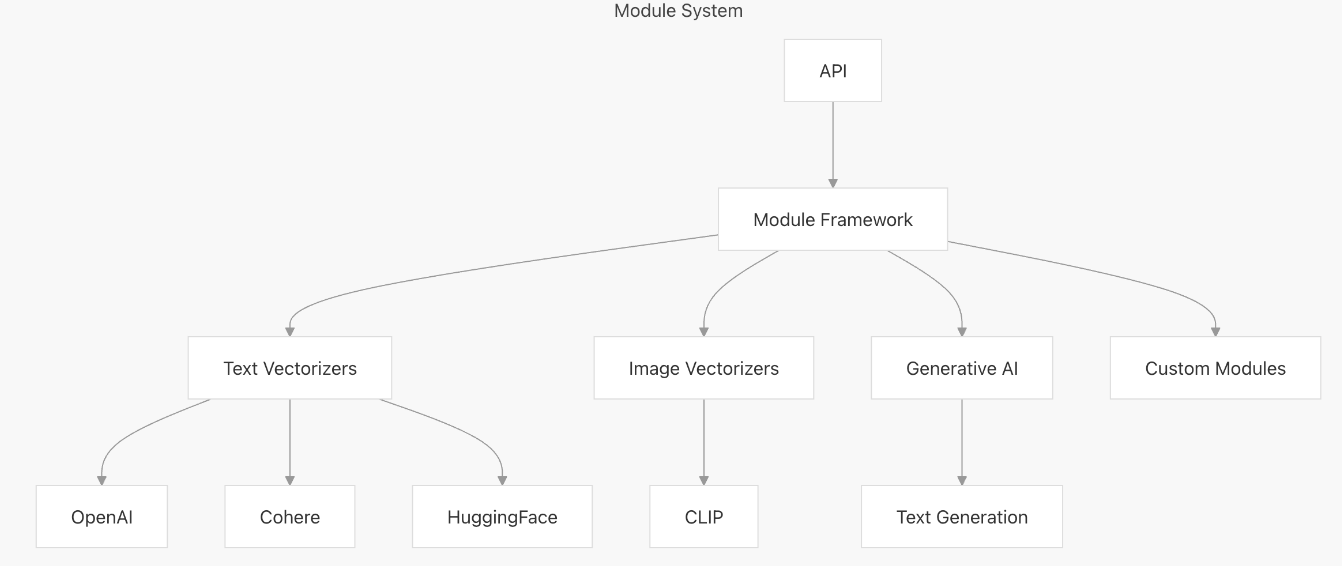
【向量库】Weaviate概述与架构解析
文章目录 一、什么是weaviate二、High-Level Architecture1. Core Components2. Storage Layer3. 组件交互流程 三、核心组件1. API Layer2. Schema Management3. Vector Indexing3.1. 查询原理3.2. 左侧:Search Process(搜索流程)3.3. 右侧&…...
