数据结构与算法(一)
文章目录
- 数据结构与算法(一)
- 1 位运算、算法是什么、简单排序
- 1.1 实现打印一个整数的二进制
- 1.2 给定一个参数N,返回1!+2!+3!+4!+...+N!的结果
- 1.3 简单排序算法
- 2 数据结构大分类、前缀和、对数器
- 2.1 实现前缀和数组
- 2.2 如何用1\~5的随机函数加工出1\~7的随机函数
- 2.3 如何把不等概率随机函数变成等概率随机函数
- 3 二分法、时间复杂度、动态数组、哈希表、有序表
- 3.1 有序数组中找到 num
- 3.2 有序数组中找到>=num最左的位置
- 3.3 有序数组中找打<=num最右的位置
- 3.4 局部最小问题
- 3.5 哈希表、有序表
- 4 链表相关的简单面试题
- 4.1 反转单链表
- 4.2 反转双链表
- 4.3 用单链表实现队列
- 4.4 用单链表实现栈
- 4.5 用双链表实现双端队列
- 4.6 K个一组翻转链表
- 4.7 两个链表相加问题
- 4.8 两个有序链表的合并
- 5 位图
- 5.1 位图
- 5.2 位运算实现加减乘除
- 6 比较器、优先队列、二叉树
- 6.1 合并多个有序链表
- 6.2 判断两棵树是否结构相同
- 6.3 判断一棵树是否是镜面树
- 6.4 返回一棵树的最大深度
- 6.5 用先序数组和中序数组重建一棵树
- 6.6 二叉树先序、中序、后序遍历的代码实现、介绍递归序
- 7 二叉树
- 7.1 二叉树按层遍历并收集节点
- 7.2 判断是否是平衡搜索二叉树
- 7.3 在二叉树上能否组成路径和
- 7.4 在二叉树上收集所有达标的路径和
- 7.5 判断二叉树是否是搜索二叉树
- 8 归并排序和快速排序
- 8.1 归并排序的递归实现和非递归实现
- 8.2 快速排序的递归实现和非递归实现
数据结构与算法(一)
1 位运算、算法是什么、简单排序
1.1 实现打印一个整数的二进制
public static void print(int num) {// int 32位,依次打印高位到低位(31 -> 0)的二进制值for (int i = 31; i >= 0; i--) {System.out.print((num & (1 << i)) == 0 ? "0" : "1");}System.out.println();
}42361845 => 00000010100001100110001111110101
Integer.MAX_VALUE => 01111111111111111111111111111111
Integer.MIN_VALUE => 10000000000000000000000000000000
1.2 给定一个参数N,返回1!+2!+3!+4!+…+N!的结果
- 方法一:
public static long f1(int n) {long ans = 0;for (int i = 1; i <= n; i++) {ans += factorial(i);}return ans;
}public static long factorial(int n) {long ans = 1;for (int i = 1; i <= n; i++) {ans *= i;}return ans;
}
- 方法二:每次都基于上次计算结果进行计算 -> 更优
public static long f2(int n) {// 第1次:1! -> cur// 第2次: 2! = 1!*2 -> cur*2 -> cur// 第3次: 3! = 2!*3 -> cur*3 -> cur// ...// 第n次: n! = (n-1)!*n -> cur*nlong ans = 0;long cur = 1;for (int i = 1; i <= n; i++) {cur = cur * i;ans += cur;}return ans;
}
1.3 简单排序算法
- 选择排序:
// [1,len) -> find minValue -> 与 0 位置交换
// [2,len) -> find minValue -> 与 1 位置交换
// ...
// [i,len) -> find minValue -> 与 i - 1 位置交换
public static void selectSort(int[] arr) {if (arr == null || arr.length < 2) return;int len = arr.length;for (int i = 0; i < len; i++) {int minValueIndex = i;for (int j = i + 1; j < len; j++) {minValueIndex = arr[j] < arr[minValueIndex] ? j : minValueIndex;}swap(arr, i, minValueIndex);}
}
- 冒泡排序:
// [0, len) -> 两两比较并交换 -> maxValue放到 len-1 位置
// [0, len-1) -> 两两比较并交换 -> maxValue放到 len-2 位置
// ...
// [0, len-i) -> 两两比较并交换 -> maxValue放到 len-i-1 位置
public static void bubbleSort(int[] arr) {if (arr == null || arr.length < 2) return;int len = arr.length;for (int i = len - 1; i >= 0; i--) {for (int j = 1; j <= i; j++) {if (arr[j - 1] > arr[j]) {swap(arr, j - 1, j);}}}
}// 优化:
public static void bubbleSort(int[] arr) {if (arr == null || arr.length < 2) return;int len = arr.length;for (int i = len - 1; i >= 0; i--) {boolean flag = false;for (int j = 1; j <= i; j++) {if (arr[j - 1] > arr[j]) {swap(arr, j - 1, j);flag = true;}}if (!flag) { // 如果没发生交换,说明已经有序,可以提前结束break;}}
}
- 插入排序:
// [0,0] -> 有序,仅一个数,显然有序
// [0,1] -> 有序 -> 从后往前两两比较并交换
// [0,2] -> 有序 -> 从后往前两两比较并交换
// ...
// [0,len-1] -> 有序 -> 从后往前两两比较并交换
public static void insertSort(int[] arr) {if (arr == null || arr.length < 2) return;int len = arr.length;for (int i = 1; i < len; i++) {int pre = i - 1;while (pre >= 0 && arr[pre] > arr[pre + 1]) {swap(arr, pre, pre + 1);pre--;}// // 写法二:
// for (int pre = i - 1; pre >= 0 && arr[pre] > arr[pre + 1]; pre--) {
// swap(arr, pre, pre + 1);
// }}
}
2 数据结构大分类、前缀和、对数器
-
内容:
-
什么是数据结构,组成各种数据结构的最基本元件?
- 数组、链表
-
前缀和数组
-
随机函数
-
对数器的使用
-
2.1 实现前缀和数组
- 求一个数组 array 在给定区间 L 到 R 之间([L,R],L<=R)数据的和。
// 方法一:每次遍历L~R区间,进行累加求和
public static class RangeSum1 {private int[] arr;public RangeSum1(int[] array) {arr = array;}public int rangeSum(int L, int R) {int sum = 0;for (int i = L; i <= R; i++) {sum += arr[i];}return sum;}
}// 方法二:基于前缀和数组,做预处理
public static class RangeSum2 {private int[] preSum;public RangeSum2(int[] array) {int N = array.length;preSum = new int[N];preSum[0] = array[0];for (int i = 1; i < N; i++) {preSum[i] = preSum[i - 1] + array[i];}}public int rangeSum(int L, int R) {return L == 0 ? preSum[R] : preSum[R] - preSum[L - 1];}
}
2.2 如何用1~5的随机函数加工出1~7的随机函数
// 此函数只能用,不能修改
// 等概率返回1~5
private static int f() {return (int) (Math.random() * 5) + 1;
}
// 等概率得到0和1
private static int f1() {int ans = 0;do {ans = f();} while (ans == 3);return ans < 3 ? 0 : 1;
}
// 等概率返回0~6
private static int f2() {int ans = 0;do {ans = (f1() << 2) + (f1() << 1) + f1();} while (ans == 7);return ans;
}
// 等概率返回1~7
public static int g() {return f2() + 1;
}public static void main(String[] args) {int testTimes = 10000000;int[] counts = new int[8];for (int i = 0; i < testTimes; i++) {int num = g();counts[num]++;}for (int i = 0; i < 8; i++) {System.out.println(i + "这个数,出现了 " + counts[i] + " 次");}
}
- 测试结果
0这个数,出现了 0 次
1这个数,出现了 1428402 次
2这个数,出现了 1427345 次
3这个数,出现了 1428995 次
4这个数,出现了 1428654 次
5这个数,出现了 1428688 次
6这个数,出现了 1428432 次
7这个数,出现了 1429484 次
2.3 如何把不等概率随机函数变成等概率随机函数
// 你只能知道,f会以固定概率返回0和1,但是x的内容,你看不到!
public static int f() {return Math.random() < 0.84 ? 0 : 1;
}// 等概率返回0和1
public static int g() {int first = 0;do {first = f(); // 0 1} while (first == f());return first;
}public static void main(String[] args) {int[] count = new int[2];// 0 1for (int i = 0; i < 1000000; i++) {int ans = g();count[ans]++;}System.out.println(count[0] + " , " + count[1]);
}
3 二分法、时间复杂度、动态数组、哈希表、有序表
- 内容:
- 二分法
- 使用二分法解决不同的题目
- 时间复杂度
- 动态数组
- 按值传递、按引用传递
- 哈希表
- 有序表
3.1 有序数组中找到 num
// arr保证有序
public boolean find(int[] arr, int num) {if (arr == null || arr.length == 0) return false;int l = 0, r = arr.length - 1;while <相关文章:
)
数据结构与算法(一)
文章目录 数据结构与算法(一)1 位运算、算法是什么、简单排序1.1 实现打印一个整数的二进制1.2 给定一个参数N,返回1!+2!+3!+4!+...+N!的结果1.3 简单排序算法2 数据结构大分类、前缀和、对数器2.1 实现前缀和数组2.2 如何用1\~5的随机函数加工出1\~7的随机函数2.3 如何把不…...
Matlab--微积分问题的计算机求解
目录 1.单变量函数的极限问题 1.1.公式例子 1.2.对应例题 1 2.多变量函数的极限问题 3.函数导数的解析解 4.多元函数的偏导数 5.Jacobian函数 6.Hessian矩阵 7.隐函数的偏导 8.不定积分问题的求解 9.定积分的求解问题 10. 多重积分的问题求解 1.单变量函数的极限问题 …...
GRU实现时间序列预测(PyTorch版)
💥项目专栏:【深度学习时间序列预测案例】零基础入门经典深度学习时间序列预测项目实战(附代码数据集原理介绍) 文章目录 前言一、基于PyTorch搭建GRU模型实现风速时间序列预测二、时序数据集的制作三、数据归一化四、数据集加载器…...

文本框粘贴时兼容Unix、Mac换行符的方法源码
本篇文章属于《518抽奖软件开发日志》系列文章的一部分。 我在开发《518抽奖软件》(www.518cj.net)的时候,要在文本框粘贴从别处复制来的名单。发现一个问题,就是一些Unix传过来的多行文本,粘贴后都变成了一行。原来&a…...
2023年华为杯研究生数学建模竞赛辅导
2023年华为杯研究生数学建模竞赛辅导 各研究生培养单位: 中国研究生数学建模竞赛作为教育部学位管理与研究生教育司指导,中国学位与研究生教育学会、中国科协青少年科技中心主办的“中国研究生创新实践系列大赛”主题赛事之一,是一项面向在校…...
post更新,put相当于删除重新增一条
索引数据 //删除后新增 PUT my_dynamic_temp/_doc/1 { “name”:“test”, “class”:“1204” } //覆盖更新 POST my_dynamic_temp/_update/1 { “doc”: { “name”:“test”, “class”:“1203”, “pernum”:“998” } }...

python责任链模式
责任链模式是一种行为设计模式,它允许你将请求沿着处理者链进行传递,直到有一个处理者能够处理它为止。在Python中,你可以使用多线程来实现责任链模式的框架。 首先,你需要定义一个基础的处理者类,它包含处理请求的方…...
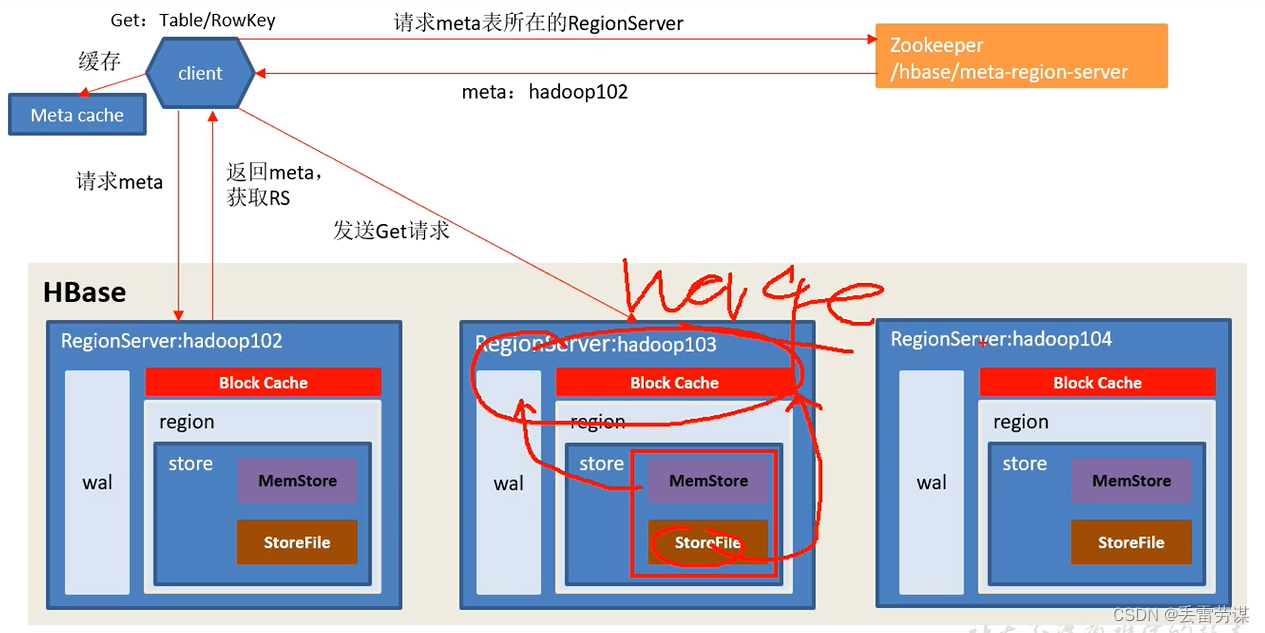
大数据技术准备
Hbase:HBase 底层原理详解(深度好文,建议收藏) - 腾讯云开发者社区-腾讯云 Hbase架构图 同一个列族如果有多个store,那么这些store在不同的region Hbase写流程(读比写慢) MemStore Flush Hbas…...

【力扣周赛】第 362 场周赛(⭐差分匹配状态压缩DP矩阵快速幂优化DPKMP)
文章目录 竞赛链接Q1:2848. 与车相交的点解法1——排序后枚举解法2——差分数组⭐差分数组相关题目列表📕1094. 拼车1109. 航班预订统计2381. 字母移位 II2406. 将区间分为最少组数解法1——排序贪心优先队列解法2——差分数组 2772. 使数组中的所有元素…...
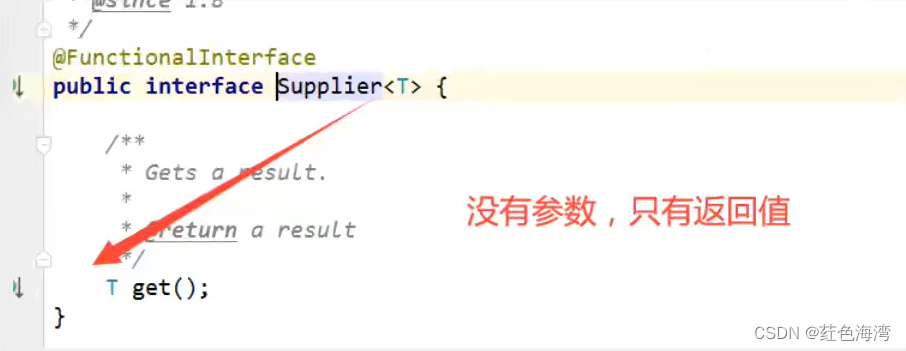
四大函数式接口(重点,必须掌握)
新时代程序员必须要会的 :lambda表达式、链式编程、函数式接口、Stream流式计算 什么是函数式接口 1.函数型接口 package com.kuang.function;import java.util.function.Function;/*** Function函数型接口 有一个输入参数,有一个输出* 只要是函数式接口…...
2023Web前端逻辑面试题
1、现有9个小球,已知其中一个球比其它的重,如何只用天平称2次就找出该球? ①把9个球分成三份,三个一份; ②拿出其中两份进行称量;会分为两种情况 若拿出的两份小球称量结果,重量相等;…...

uniapp中git忽略node_modules,unpackage文件
首先在当前项目的命令行新建.gitignore文件: touch .gitignore再在编辑器中打开该文件,并在该文件中加入需要忽略的文件名: node_modules/ .project unpackage/ .DS_Store 提示:如果以前提交过unpackage文件的话,需…...

Json-Jackson和FastJson
狂神: 测试Jackson 纯Java解决日期格式化 设置ObjectMapper FastJson: 知乎:Jackson使用指南 1、常见配置 方式一:yml配置 spring.jackson.date-format指定日期格式,比如yyyy-MM-dd HH:mm:ss,或者具体的…...

RK3588 点亮imx586摄像头
一.硬件原理图 mipi摄像头硬件确认点: 1.供电:5V,2.8V,1.2V,1.8V,reset脚(硬拉3.3,上电的时候从低到高),pwron脚外接 3.3V。 2,时钟:MCLKOUT是2…...
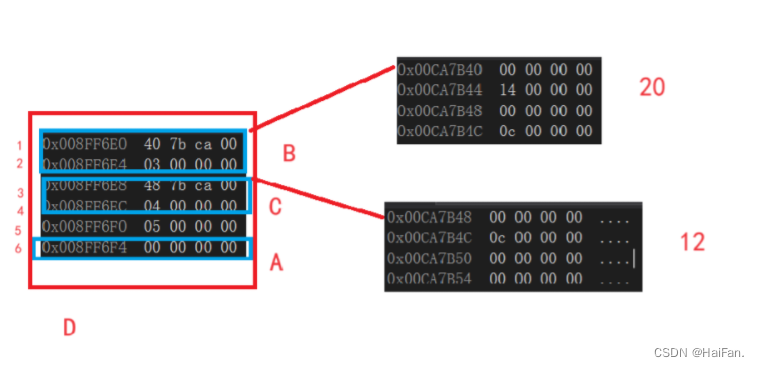
C++---继承
继承 前言继承的概念及定义继承的概念继承定义继承关系和访问限定符 基类和派生类对象赋值转换继承中的作用域派生类的默认成员函数继承与友元继承与静态成员**多重继承**多继承下的类作用域菱形继承虚继承使用虚基类 支持向基类的常规类型转换 前言 在需要写Father类和Mother…...

使用新版Maven-mvnd快速构建项目
目前我们项目的构建方式多数是 maven、gradle,但是 maven 相对 gradle 来说,构建速度较慢,特别是模块相对较多的时候,构建速度更加明显。但是我们将项目由 maven 替换为 gradle 相对来说会比较麻烦,成本较高。于是我们…...
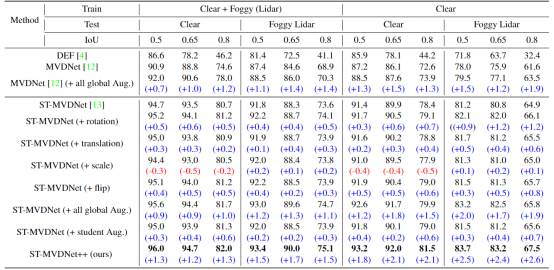
【ICASSP 2023】ST-MVDNET++论文阅读分析与总结
主要是数据增强的提点方式。并不能带来idea启发,但对模型性能有帮助 Challenge: 少有作品应用一些全局数据增强,利用ST-MVDNet自训练的师生框架,集成了更常见的数据增强,如全局旋转、平移、缩放和翻转。 Contributi…...
MySQL 面试题——MySQL 基础
目录 1.什么是 MySQL?有什么优点?2.MySQL 中的 DDL 与 DML 是分别指什么?3.✨数据类型 varchar 与 char 有什么区别?4.数据类型 BLOB 与 TEXT 有什么区别?5.DATETIME 和 TIMESTAMP 的异同?6.✨MySQL 中 IN …...
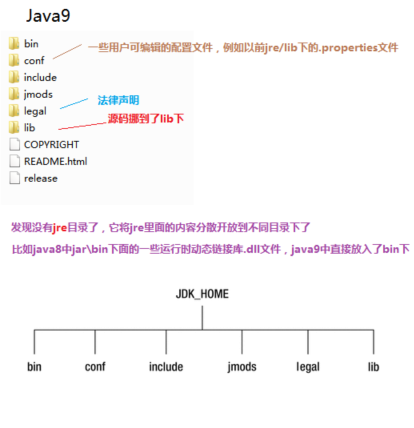
JDK9特性——概述
文章目录 引言JDK9特性概述JDK9的改变JDK和JRE目录变化总结 引言 JAVA8 及之前,版本都是特性驱动的版本更新,有重大的特性产生,然后进行更新。 JAVA9开始,JDK开始以时间为驱动进行更新,以半年为周期,到时…...

征战开发板从无到有(三)
接上一篇,翘首已盼的PCB板子做好了,管脚约束信息都在PCB板上体现出来了,很满意,会不会成为爆款呢,嘿嘿,来,先看看PCB裸板美图 由于征战开发板电路功能兼容小梅哥ACX720,大家可以直…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...
