v-if失效原因
一般v-if失效都是和绑定变量有关,我所知道的一般有两种
1.绑定的变量为String类型或者其他类型
就是返回的变量类型与所需要的布尔类型不匹配。
<template><div><div id="container" ref="container" v-if='type'></div></div>
</template>
<script setup lang="ts">const type=ref('false')
</script>
就像这种,我们得到的type的值是"false"而不是false,两者之间类型不同。如果不确定变量类型,就用typeof去打印。
2.两个相似的组件,v-if无法就行判断
对于两个很相似的组件,不管自定义还是还是本身的,如果只是用v-if那可能会造成失效
<template><div><el-button v-if='type'></el-button><el-button v-if='!type'></el-button></div>
</template>
<script setup lang="ts">const type=ref(false)
</script>
就像这样的,但是我们可以通过添加key值去区分。
<template><div><el-button v-if='type' key=1></el-button><el-button v-if='!type' key=2></el-button></div>
</template>
<script setup lang="ts">const type=ref(false)
</script>
这样就可以生效了。
相关文章:

v-if失效原因
一般v-if失效都是和绑定变量有关,我所知道的一般有两种 1.绑定的变量为String类型或者其他类型 就是返回的变量类型与所需要的布尔类型不匹配。 <template><div><div id"container" ref"container" v-iftype></div>&l…...
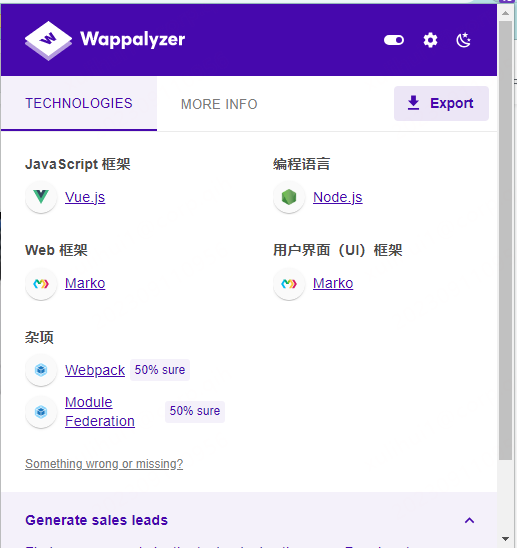
Chrome 基于 Wappalyzer 查看网站所用的前端技术栈
1. 找到谷歌商店 https://chrome.google.com/webstore/search/wappalyzer?utm_sourceext_app_menu 2. 搜索 Wappalyzer 3. 添加至Chrome 4. 使用 插件 比如打开 https://www.bilibili.com/ 就可以看到其所以用的前端技术栈了...

python的装饰器
作用:在不改变原来函数的代码情况下,进行修改,或者增加函数的功能装饰器本质上就是一个闭包雏形:def wrapper(fn): wrapper: 装饰器 , fn: 目标函数def inner():# 在目标函数执行前的一些动作fn()# 在目标函数执行后的一些动作return inner #千万别加(),这里是返回一…...
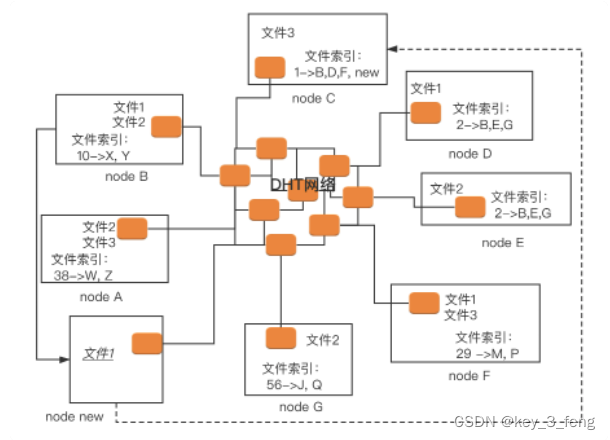
P2P协议的传输艺术
TP 采用两个 TCP 连接来传输一个文件。 控制连接:服务器以被动的方式,打开众所周知用于 FTP 的端口 21,客户端则主动发起连接。该连接将命令从客户端传给服务器,并传回服务器的应答。常用的命令有:list——获取文件目…...
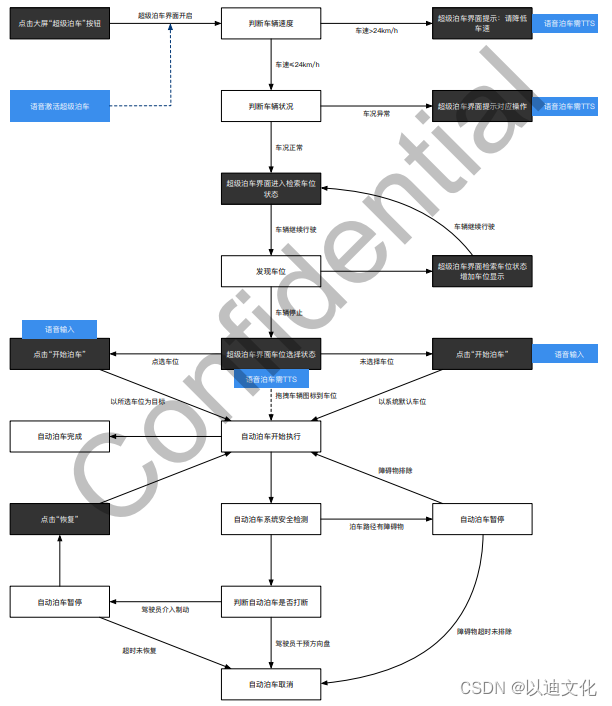
辅助驾驶功能开发-功能规范篇(21)-4-XP行泊一体方案功能规范
XPilot Parking 自动泊车系统 • 超级自动泊车辅助(Super AutoParking Assist)、语音控制泊车辅助(Autoparking with Speech) - 产品定义 超级自动泊车辅助是⼀个增强的自动泊车辅助系统。在超级自动泊车辅助系统中,识别车位将会变得实时可见, 并且不可泊入的⻋位也将…...

家政服务小程序上门服务小程序预约上门服务维修保洁上门服务在线派单技师入口
套餐一:源码=1500元 套餐二:全包服务 包服务器+域名+认证小程序+搭建+售后=2000元 主要功能: 1、服务商入驻 支持个人或企业入驻成为平台服务商; 2、发布商品 入驻服务商后,可以发布服务商品,用户可以在线下单,预约服务; 3、发布需求 用户可以发布一口价或竞价需求…...

LeetCode精选100题-【3数之和】-2
这里写自定义目录标题 解法1:解法2: 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请你返回所有和为 0 且不重复的三元组。注意:答案中不…...

springboot集成mybatis-plus
一、在spring boot中配置mybatis-plus 1、创建一个spring boot项目,注意勾选mysql 2、在pom.xml文件中添加mybatis-plus的依赖包 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0&qu…...

再想一想GPT
一 前言 花了大概两天时间看完《这就是ChatGPT》,触动还是挺大的,让我静下来,认真地想一想,是否真正理解了ChatGPT,又能给我们以什么样的启发。 二 思考 在工作和生活中,使用ChatGPT或文心一言,…...
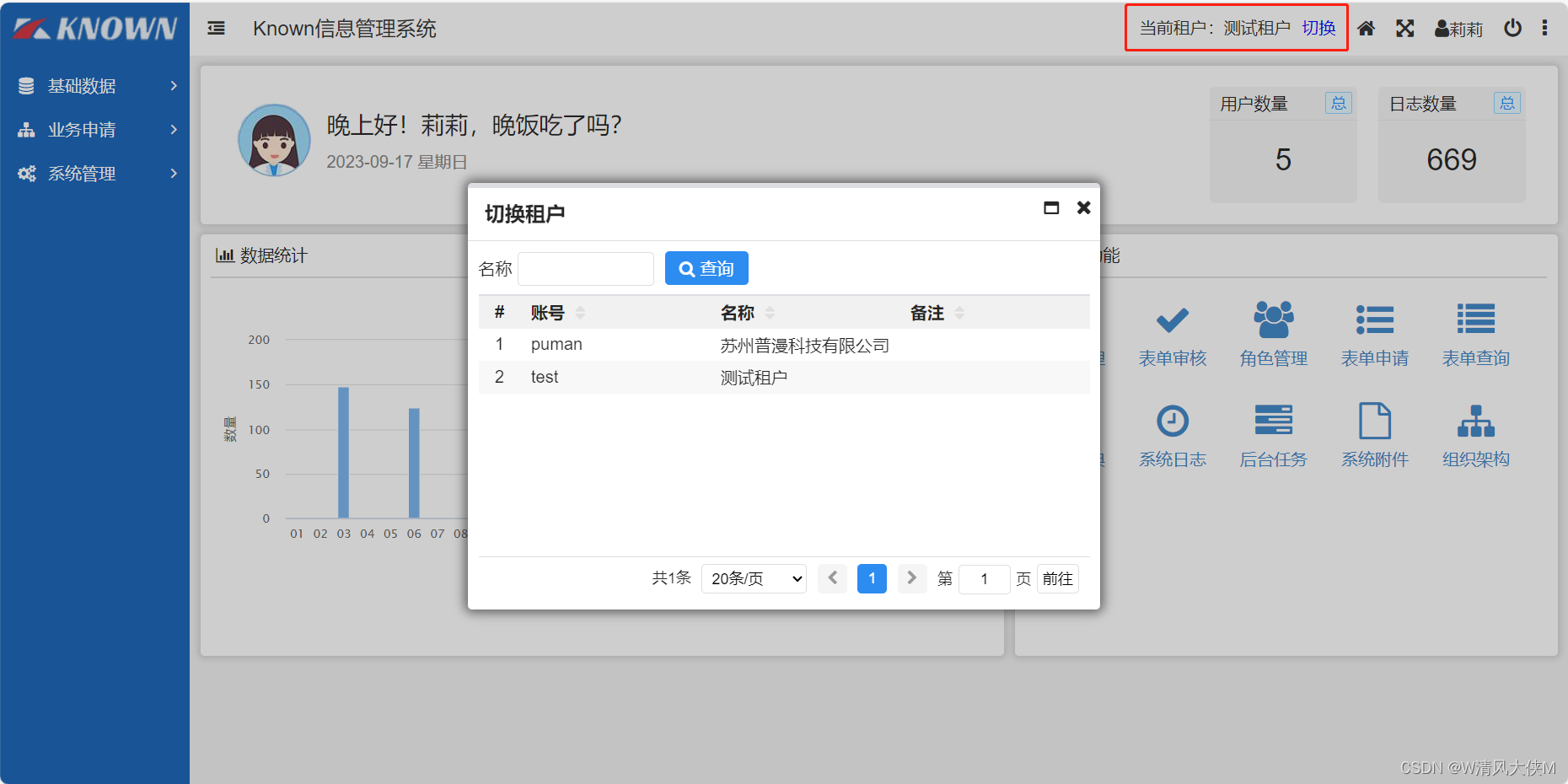
Blazor前后端框架Known-V1.2.15
V1.2.15 Known是基于C#和Blazor开发的前后端分离快速开发框架,开箱即用,跨平台,一处代码,多处运行。 Gitee: https://gitee.com/known/KnownGithub:https://github.com/known/Known 概述 基于C#和Blazo…...
Tomcat 的部署和优化
目录 1、什么是Tomcat 1.1、静态页面的选择 2、Tomcat是怎么运行的 3、安装jdk & 部署jdk环境 & Tomcat 安装 1、安装jdk 2、配置jdk环境变量 3、tomcat安装 4、Tomcat启动 5.优化tomcat启动速度 6.Tomcat的主要命令 7.Tomcat 配置虚拟主机 8.Tomca…...
后端中间件安装与启动(Redis、Nginx、Nacos、Kafka)
后端中间件安装与启动 RedisNginxNacosKafka Redis 1.打开cmd终端,进入redis文件目录 2.输入redis-server.exe redis.windows.conf即可启动,不能关闭cmd窗口 (端口配置方式:redis目录下的redis.windows.conf配置文件,…...

【电子元件】常用电子元器件的识别之电阻器
目录 前言1. 电阻器的识别1.1 普通电阻器的识别1. 普通电阻器的识别色环电阻器绕线电阻器水泥电阻器贴片电阻器网络电阻器(排阻)保险电阻器精密电阻器2. 电阻器的符号3. 普通电阻器的主要参数标称阻值和允许误差额定功率最高工作电压温度系数1.2 电位器的识别1. 电位器的识别…...

指针和数组笔试题讲解(2)
🐵本篇文章将会对上篇一维数组笔试题的剩余部分和二维数组的笔试题进行讲解 一、一维数组 1>试题部分(一)✏️ char* p "abcdef";printf("%zd\n", sizeof(p)); printf("%zd\n", sizeof(p 1)); printf("%zd\n", sizeo…...

MapReduce YARN 的部署
1、部署说明 Hadoop HDFS分布式文件系统,我们会启动: NameNode进程作为管理节点DataNode进程作为工作节点SecondaryNamenode作为辅助 同理,Hadoop YARN分布式资源调度,会启动:ResourceManager进程作为管理节点NodeM…...

vue 引入zTree
下载js包解压后找个地方放文件夹内 引入 import "/common/zTree/js/jquery-1.4.4.min" import "/common/zTree/js/jquery.ztree.core.min.js" import "/common/zTree/js/jquery.ztree.excheck.min.js" import "/common/zTree/css/metroSt…...

链队列的基本操作(带头结点,不带头结点)
结构体 typedef struct linknode{int data;struct linknode* next;后继指针 }linknode; typedef struct {linknode* front, * rear;//队头队尾指针 }linkquene; 初始化队列(带头结点) int initquene(linkquene* q)//初始化队列 {q->front q->r…...

深入学习 Redis Cluster - 基于 Docker、DockerCompose 搭建 Redis 集群,处理故障、扩容方案
目录 一、基于 Docker、DockerCompose 搭建 Redis 集群 1.1、前言 1.2、编写 shell 脚本 1.3、执行 shell 脚本,创建集群配置文件 1.4、编写 docker-compose.yml 文件 1.5、启动容器 1.6、构建集群 1.7、使用集群 1.8、如果集群中,有节点挂了&am…...
笔记)
C现代方法(第3、4章)笔记
文章目录 C现代方法笔记(chapter3&4)第3章 格式化输入/输出3.1 printf函数3.1.1 转换说明3.1.2 转义序列 3.2 scanf函数3.2.1 scanf函数的工作方法3.2.2 格式串中的普通字符3.2.3 易混淆的printf函数和scanf函数 问与答编程题 第4章 表达式4.1 算术运…...
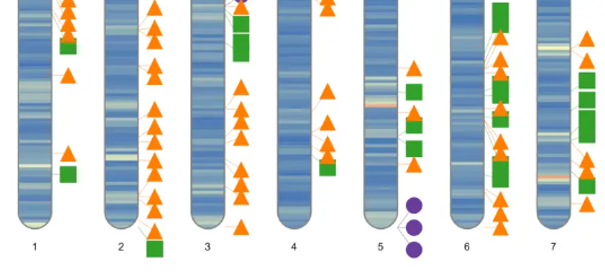
R语言绘制染色体变异位置分布图,RIdeogram包
变异位点染色体分布图 今天分享的内容是通过RIdeogram包绘制染色体位点分布图,并介绍一种展示差异位点的方法。 在遗传学研究中,通过测序等方式获得了基因组上某些位置的基因型信息。 如下表,第一列是变异位点的ID,第二列是染色体…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
