【数据结构与算法】算法的时间复杂度和空间复杂度

文章目录
- 前言
- 1.算法效率
- 1.1.如何衡量一个算法的好坏
- 1.2.算法的复杂度
- 2.时间复杂度
- 2.1.时间复杂度的概念
- 2.2.大O的渐进表示法
- 2.3.常见时间复杂度计算举例
- 2.4.常见时间复杂度
- 3.空间复杂度
- 4.复杂度oj练习
- Practice.1 消失的数字
- Practice.2 旋转数组
- 写在最后
前言
关于时空复杂度的分析,是每一个程序员的必备技能,本文将带你了解什么是时空复杂度?熟知怎样去计算一个算法的
时间复杂度和空间复杂度。
1.算法效率
1.1.如何衡量一个算法的好坏
如何衡量一个算法的好坏呢?我们先看一段代码:
int Fib(int N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
-
这段代码是计算第
N个斐波那契数列的数是多少,可以看到,此算法采用的是递归,代码简洁,但简洁一定就好么?那么我们又该如何衡量其好坏呢? -
我们可以通过对代码的复杂度进行分析,从而得出其时间效率和空间效率,依此来衡量其好坏。
1.2.算法的复杂度
-
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
-
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
-
一般的,越复杂的代码,我们越难去计算其时间复杂度和空间复杂度, 这就需要我们长期的练习来增强我们对复杂度的敏感度以及对一个题目如何找出最优解的思想。
-
可能我们在平时写代码的时候,难以体会到复杂度好坏对程序的影响,但如果是一个大型项目,复杂度的好坏就显得尤为重要,这直接关乎到用户体验感的好坏,因此,一个程序复杂度的好坏是很重要的 。
2.时间复杂度
2.1.时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
例如:
<请计算一下Func1中++count语句总共执行了多少次?>
void Func1(int N)
{int count = 0;for (int i = 0; i < N ; ++ i){for (int j = 0; j < N ; ++ j){++count;}}for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
Func1 执行的基本操作次数 :

当N为不同值时,对应的次数:
N = 10 F(N) = 130
N = 100 F(N) = 10210
N = 1000 F(N) = 1002010
但是,实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
2.2.大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
- 用常数
1取代运行时间中的所有加法常数。 - 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是
1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:
N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。另外有些算法的时间复杂度存在最好、平均和最坏情况:
- 最坏情况:任意输入规模的最大运行次数(上界)
- 平均情况:任意输入规模的期望运行次数
- 最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
- 最好情况:
1次找到 - 最坏情况:
N次找到 - 平均情况:
N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
2.3.常见时间复杂度计算举例
实例1:
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}

实例2:
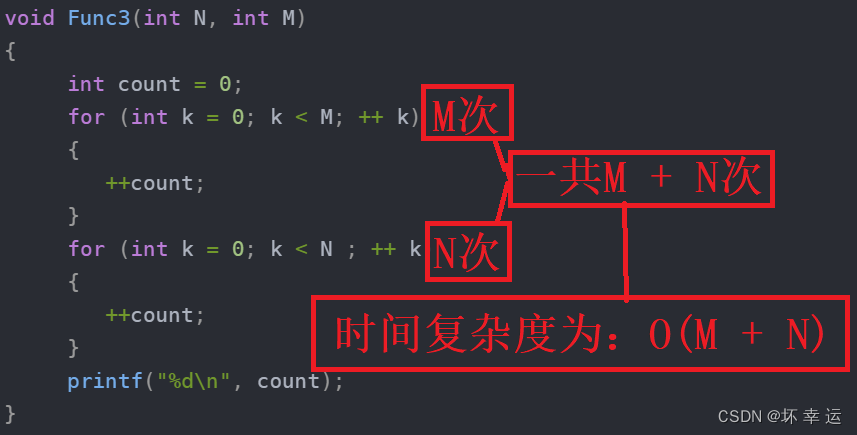
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}
实例3:
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}
这里
count只加了100次,对于是常数次的情况,一律为O(1);
实例4:
// 计算strchr的时间复杂度?
const char * strchr ( const char * str, int character );
该例子基本操作执行最好
1次,最坏N次,时间复杂度一般看最坏,时间复杂度为 O(N)
实例5:
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
实例5基本操作执行最好
N次,最坏执行了N*(N+1)/2次,通过推导大O阶方法+时间复杂度一般看最
坏,时间复杂度为O(N^2)
实例6:
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}
该例子基本操作执行最好
1次,最坏O(logN)次,时间复杂度为O(logN)
注意: logN在算法分析中表示是底数为2,对数为N。有些地方会写成lgN。(建议通过折纸查找的方式讲解logN是怎么计算出来的)
此算法为二分查找:通过与目标数的大小的比较,每次将搜索范围除以2,这种算法时间效率非常的高,但前提是,查找的数组是要有序的。也因此该算法很少被用到,因为要将一个数组排序,一般最低的时间效率为O(N*logN)。
实例7:
//计算一个数的阶乘递归写法
int Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}
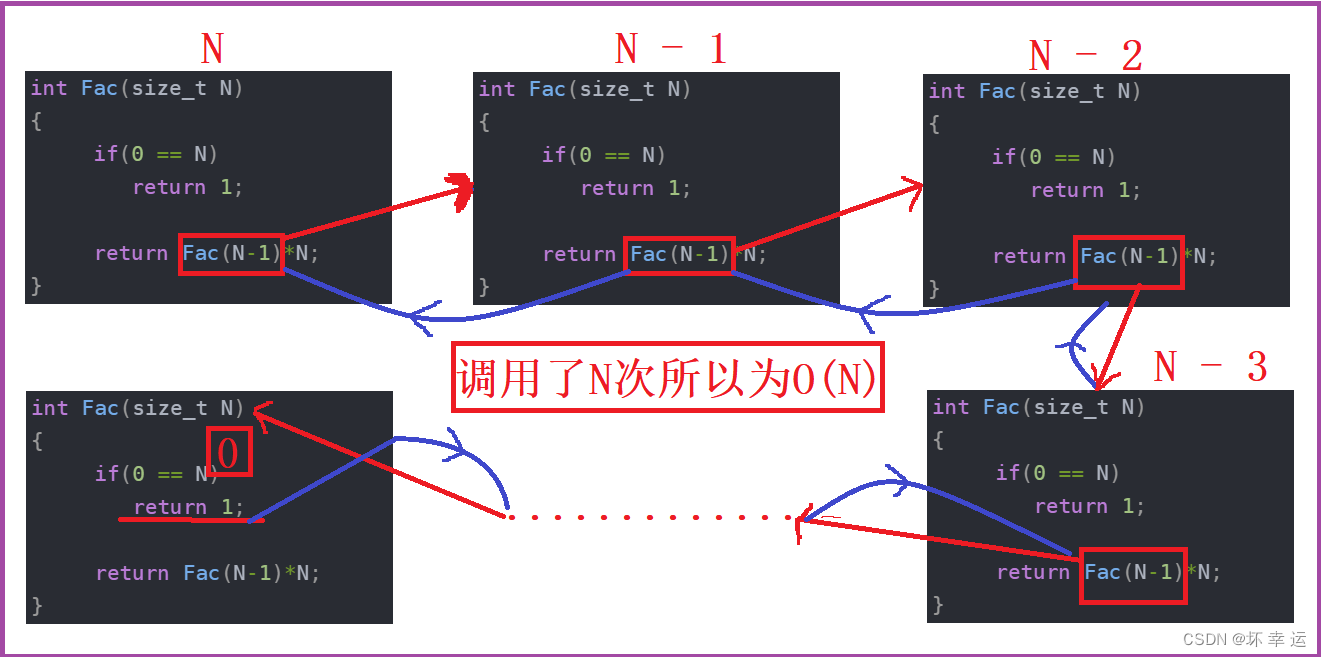
实例8:
// 计算斐波那契递归Fib的时间复杂度?
int Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
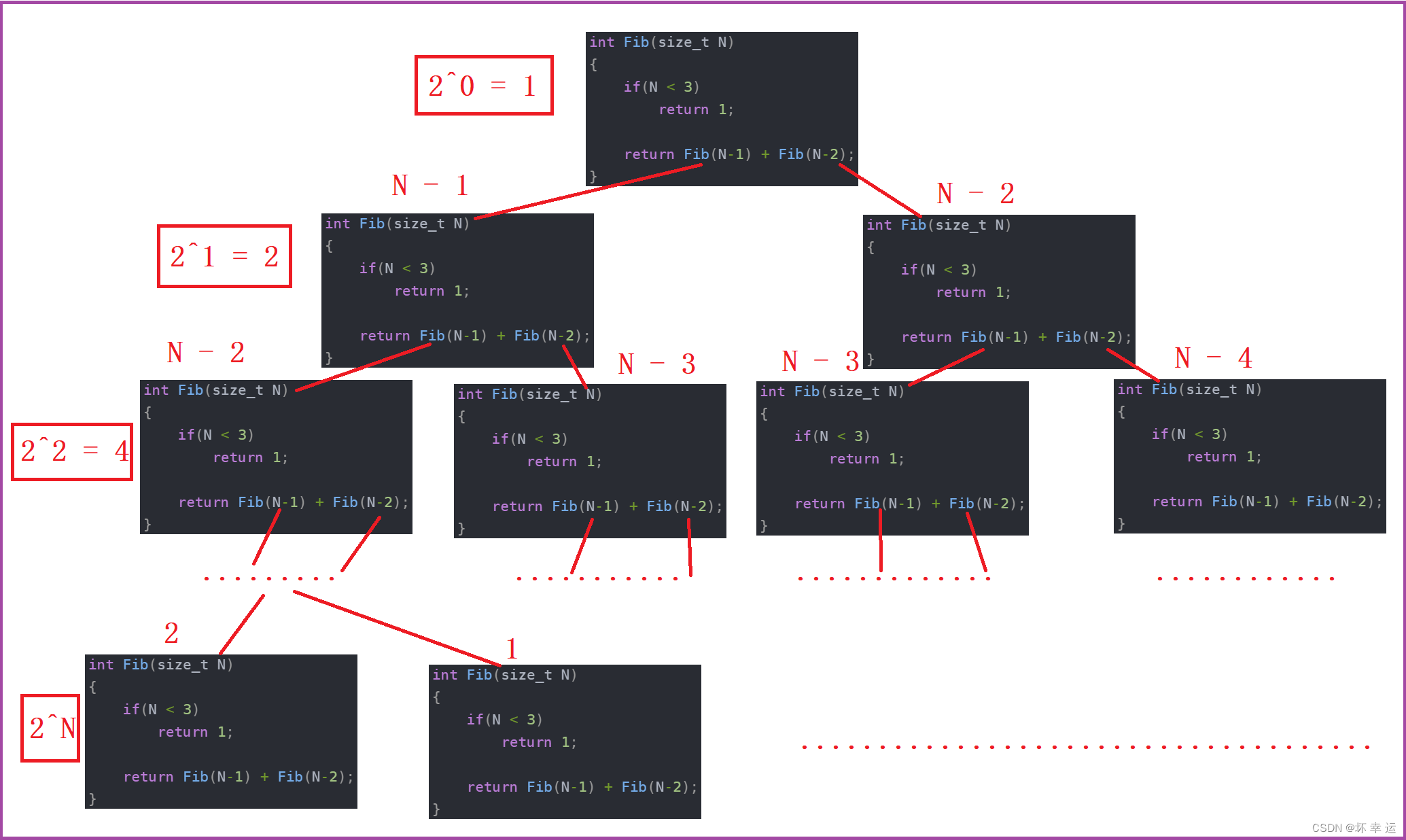
该例子通过计算分析发现基本操作递归了
2^N次,时间复杂度为O(2^N)。
2.4.常见时间复杂度

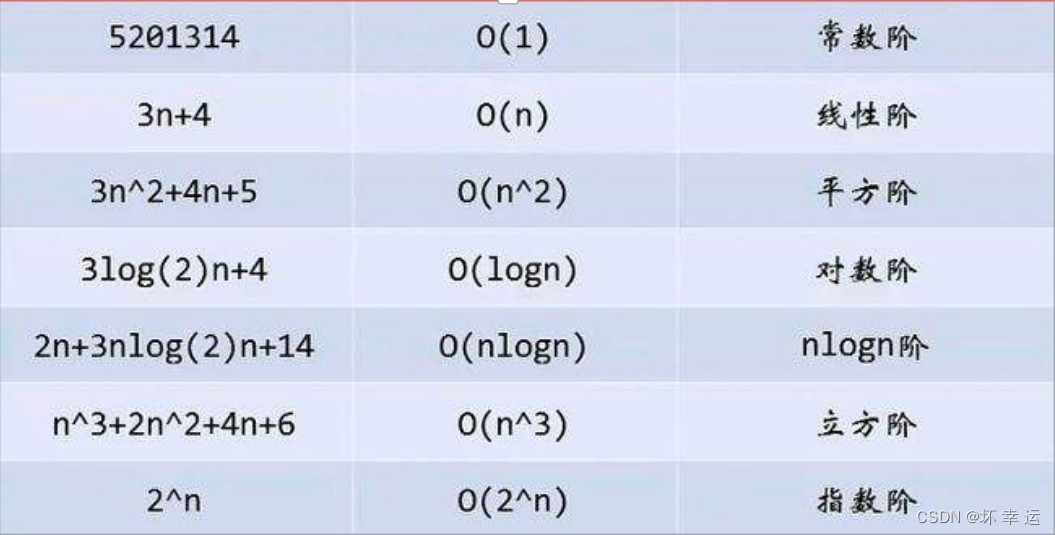
3.空间复杂度
- 空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度。
- 空间复杂度不是程序占用了多少
bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
示例1:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}

示例2:
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if(n==0)return NULL;// 这里开辟了n + 1个空间long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}
该示例动态开辟了
N + 1个空间,空间复杂度为O(N)
示例3:
// 计算阶乘递归Fac的空间复杂度?
int Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}
该示例递归调用了
N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
4.复杂度oj练习
Practice.1 消失的数字
相关题目链接:Let’ s go!
- 这道题如果是暴力解法的话,最坏是
O(N^2):将0~n中的每一个数在数组中遍历一次,如果在数组中没有找到与这个数相等的数,那这个数就是消失的数字; - 由于只缺失了一个数,所以这里我们可以分别对
数组和0~n个数进行求和,相减既是那个消失的数。整个过程,两个for循环,第一个遍历数组为n次,第二个为n + 1次,因此时间复杂度为:O(N), 而这里创建的变量为常数,因此空间复杂度为:O(1)。
int missingNumber(int* nums, int numsSize){int sum1 = 0, sum2 = 0;for (int i = 0; i < numsSize; i++) sum1 += nums[i];for (int i = 0; i <= numsSize; i++) sum2 += i;return sum2 - sum1;
}
- 由题,遍历
数组和遍历0~n,其中只有那个消失的数遍历了一次,其它的数都出现了两次,因此我们可以对数组和0~n个数同时按位异或(如果两个相同的数异或,结果为0, 任意一个数与0异或结果都是这个数本身)来找出那个消失的数。整个过程很容易看出时间复杂度为:O(N),空间复杂度为:O(1).
int missingNumber(int* nums, int numsSize){int ret = 0;for (int i = 0; i < numsSize; i++) ret ^= nums[i];for (int i = 1; i <= numsSize; i++) ret ^= i;return ret;
}
Practice.2 旋转数组
相关题目链接:Let’ s go!
-
该题如果是依次挪动数据的话,最坏的情况是
k = n(数组长度)- 1,此时为(n - 1) * n, 因此时间复杂度为O(N),空间复杂度为:O(1); -
比较容易想到的提高时间效率的算法:我们可以使用额外的数组来将每个元素放至正确的位置,要挪动的数依次放入开辟的数组的前面,然后再将前面不旋转的数放置开辟的数组的后面,这样是以空间换时间,所以整体时间复杂度为:
O(N),空间复杂度为:O(N)。 -
难想到的一种算法是:先将前
n(为数组长度)-k个数翻转,再将后k个数翻转,最后整体翻转。这样的话,能够将整段代码的效率升至最高,时间复杂度为:O(N),空间复杂度为:O(1).
代码实现:
void reverse(int* a, int l, int r)
{assert(a);while (l < r){int tmp = a[l];a[l] = a[r];a[r] = tmp;l++;r--;}
}void rotate(int* nums, int numsSize, int k){k %= numsSize;reverse(nums, 0, numsSize - k - 1);reverse(nums, numsSize - k, numsSize - 1);reverse(nums, 0, numsSize - 1);
}
写在最后
对一段代码的时间复杂度和空间复杂度的分析熟练度客观上体现了你的算法水平,因此,我们在学好算法的道路上要一步一个脚印,切不可投机取巧。
感谢阅读本小白的博客,错误的地方请严厉指出噢!
相关文章:

【数据结构与算法】算法的时间复杂度和空间复杂度
文章目录前言1.算法效率1.1.如何衡量一个算法的好坏1.2.算法的复杂度2.时间复杂度2.1.时间复杂度的概念2.2.大O的渐进表示法2.3.常见时间复杂度计算举例2.4.常见时间复杂度3.空间复杂度4.复杂度oj练习Practice.1 消失的数字Practice.2 旋转数组写在最后前言 关于时空复杂度的分…...

不使用contab -e的方式,添加计划任务
不使用contab -e的方式,添加计划任务 crond 服务的周期任务的文件存放位置在:/var/spool/cron/ 如果你是root用户的话那么你的周期任务文件名就叫root 如果你使用其他用户创建的周期任务,任务文件名就叫它本身 1、 使用root用户创建周期任…...

sentry2摄像头之blink篇
一、硬件 arduino sentry2摄像头 二、实验内容 第一步 安装好esp8266库函数 具体详见ES826安装指导,CSDN有很多资源,或者浏览 https://tosee.readthedocs.io/zh/latest/ 网址 第二步 配置 详情见视频,有简单讲解 视频1:电脑端配置 https://live.csdn.net/v/277427 视频2:s…...

springboot集成PDF导出
内容目录 知识准备 什么是itext itext的历史版本和License问题 标准的itextpdf导出的步骤 实现案例 Pom依赖 导出PDF 添加页眉页脚和水印 进一步理解 遇到license问题怎么办 为何添加页眉页脚和水印是通过PdfPageEvent来完成 除了处理word, excel等文件外,最为常见的…...

Podman 创建持久 MySQL 数据库容器
使用正确的 SELinux 上下文和权限创建目录/home/student/local/mysql。 创建/home/student/local/mysql目录。 [studentworkstation ~]$ mkdir -vp /home/student/local/mysql mkdir: 创建的目录/home/student/local mkdir: 创建的目录/home/student/local/mysql/home/studen…...

Java-反射
反射概述 Java反射机制: 是指在运行时去获取一个类的变量和方法信息。然后通过获取的信息来创建对象,调用方法的一种机制。由于这种<动态性>,可以极大的增强程序的灵活性,程序不用在编译期就完成确定,在运行期仍…...

构造agent类型的内存马(内存马系列篇十三)
写在前面 前面我们对JAVA中的Agent技术进行了简单的学习,学习前面的Agent技术是为了给这篇Agent内存马的实现做出铺垫,接下来我们就来看看Agent内存马的实现。 这是内存马系列篇的第十三篇了。 环境搭建 我这里就使用Springboot来搭建一个简单的漏洞…...
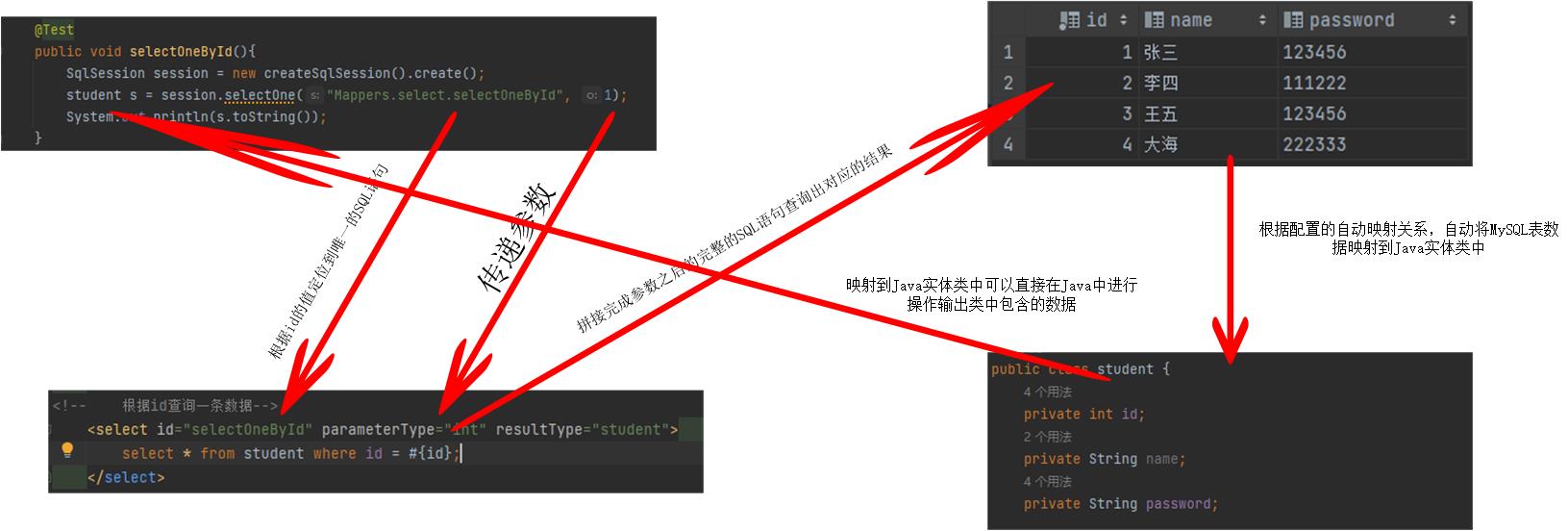
JavaEE简单示例——<select>中的查询参数传递和结果集封装自动映射关系
简单介绍: 在之前我们在讲SQL映射文件中的映射查询语句的<select>标签的时候,对其中的四个常用属性的讲解并不是那么的透彻,今天就来详细的解释<select>的四个常用属性的具体含义以及<select>标签在进行查询的时候查询参数…...

信息安全圈都在谈论CISP,CISSP,这两者有什么区别呢?
CISP 和 CISSP 都是信息安全认证资格考试,但是它们之间有一些区别。 CISP(Certified Information Security Professional)认证考试是由国际信息系统安全认证联盟(ISC)所开发和管理的,主要考核信息安全专业人员在保障企…...
浅谈Redisson实现分布式锁的原理
1.Redisson简介 Redis 是最流行的 NoSQL 数据库解决方案之一,而 Java 是世界上最流行(注意,我没有说“最好”)的编程语言之一。虽然两者看起来很自然地在一起“工作”,但是要知道,Redis 其实并没有对 Java…...
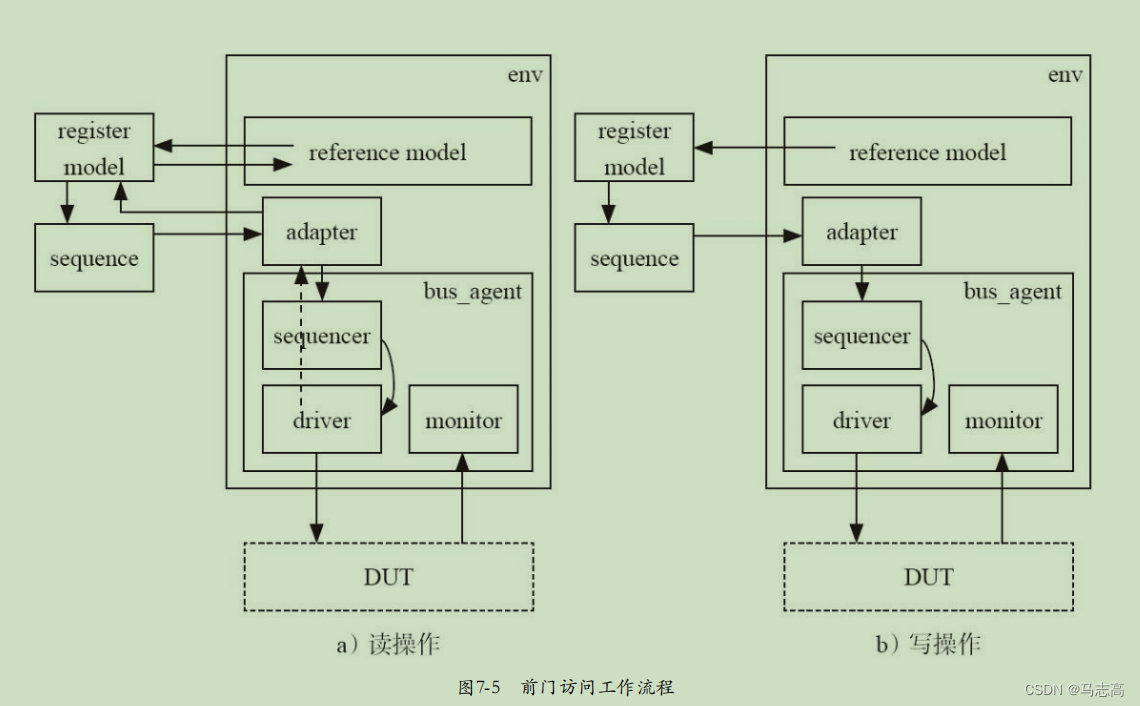
UVM实战(张强)-- UVM中的寄存器模型
目录一.整体的设计结构图二.各个组件代码详解2.1 DUT2.2 bus_driver2.3 bus_sequencer2.4 bus_monitor2.5 bus_agent2.6 bus_transaction2.7 bus_if2.8 my_if2.9 my_transaction2.10 my_sequencer2.11 my_driver2.12 my_monitor2.13 my_agent2.14 my_scoreboard2.15 my_env2.16…...
什么是 CSAT?这份客户满意度流程指南请查收
什么是 CSAT?如何计算我的客户满意度分数?大中型公司应该熟悉这些术语。以下文章旨在教您有关客户满意度流程的所有内容 - 基本的CSAT概念、创建CSAT调查的好处、如何创建CSAT调查。配图来源: SaleSmartly(ss客服) 一、什么是 CSAT࿱…...

AD域备份和恢复工具
Microsoft的本地Active Directory备份和恢复功能不适用于对象级备份和属性级还原。使用RecoveryManager Plus,您不仅可以备份和还原所有AD对象,还可以备份和还原其他基本AD元素,例如架构属性,组成员身份信息和Exchange属性。此外&…...

老学长的浙大MPA现场复试经验分享
作为一名在浙大MPA项目已经毕业的考生来说,很荣幸受到杭州达立易考周老师的邀请,给大家分享下我的复试经验,因为听周老师说是这几年浙大MPA因疫情情况,已经连续几年都是线上个人复试了,而今年疫情社会面较为平稳的情况…...

制作证书链并进行验证
生成自签名的根证书: openssl req -x509 -newkey rsa -outform PEM -out tls-rootca.pem -keyform PEM -keyout tls-rootca.key.pem -days 35600 -nodes -subj “/C=cn/O=mycomp/OU=mygroup/CN=rootca” 生成中间证书 1.生成csr和key文件 openssl req -newkey rsa:2048 -outf…...
基于python多光谱遥感数据处理、图像分类、定量评估及机器学习方法应用
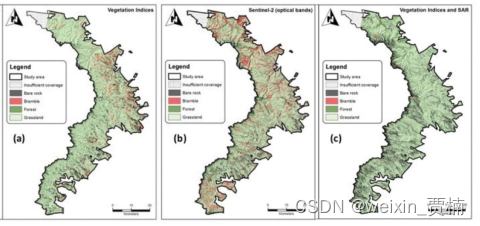
基于卫星或无人机平台的多光谱数据在地质、土壤调查和农业等应用领域发挥了重要作用,在地质应用方面,综合Aster的短波红外波段、landsat热红外波段等多光谱数据,可以通过不同的多光谱数据组合,协同用于矿物信息有效提取。此外&…...

初识 git--本地仓库
目录:一,基础步骤:1,安装2,配置3,检查配置4,创建仓库 - repository5,查看工作区的文件状态6,如果显示乱码的解决方式git status 显示乱码终端乱码7,添加工作区…...
Redis学习之持久化(六)
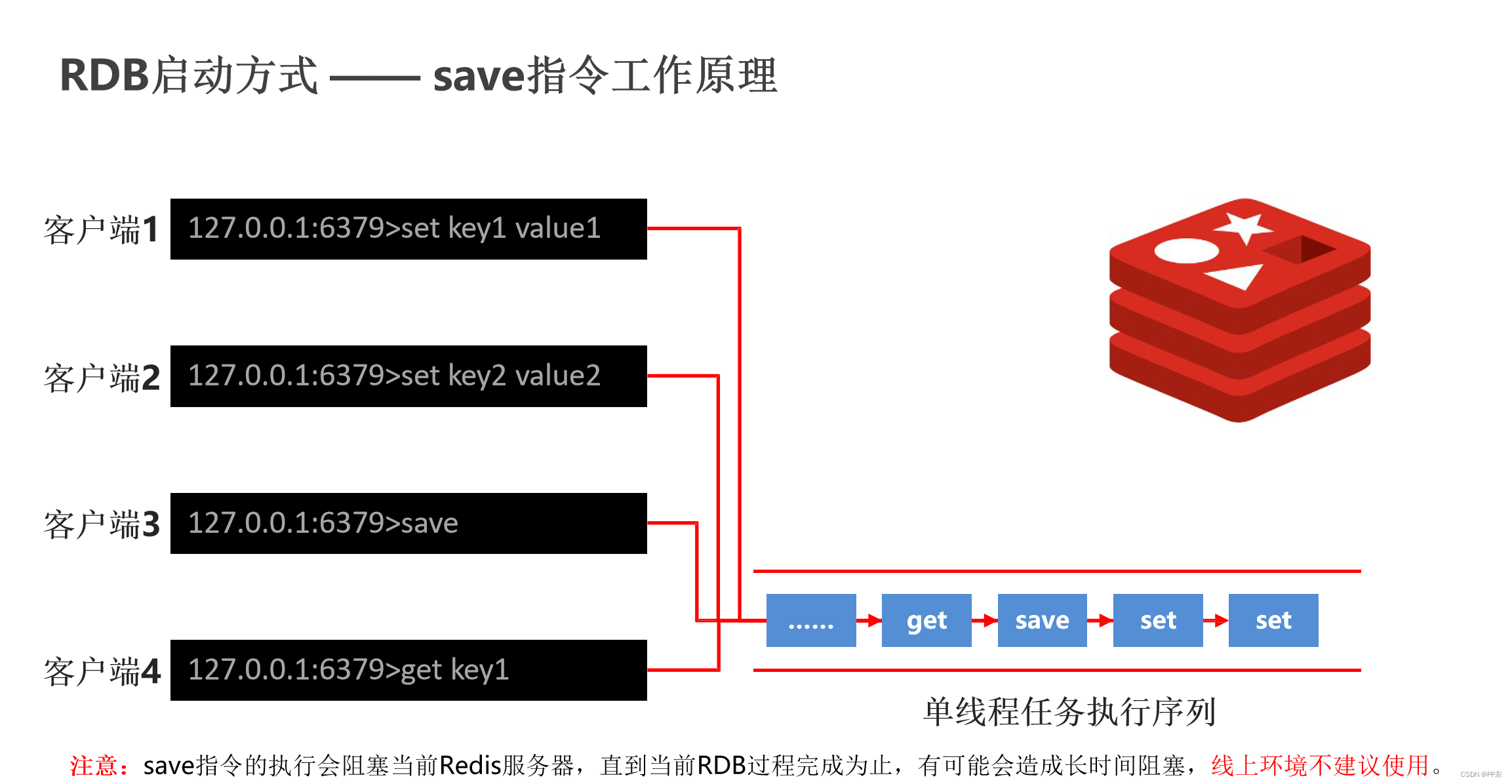
这里写目录标题一、持久化简介1.1 持久化1.2 Redis持久化的两种形式二、RDB2.1 RDB概念2.2 save指令手动执行一次保存配置相关参数2.3 bgsave指令2.4 save配置自动执行2.5 RDB三种启动方式对比三、AOF3.1 AOF概念3.2 AOF执行策略3.3 AOF重写四、RDB和AOF区别2.1 RDB与AOF对比&a…...

C++11 之 auto decltype
文章目录autodecltypesauto 和 decltype 的配合—返回值类型后置关于 c11 新特性,最先提到的肯定是类型推导,c11 引入了 auto 和 decltype 关键字,使用他们可以在编译期就推导出变量或者表达式的类型,方便开发者编码也简化了代码。…...
论文笔记:How transferable are features in deep neural networks? 2014年NIP文章
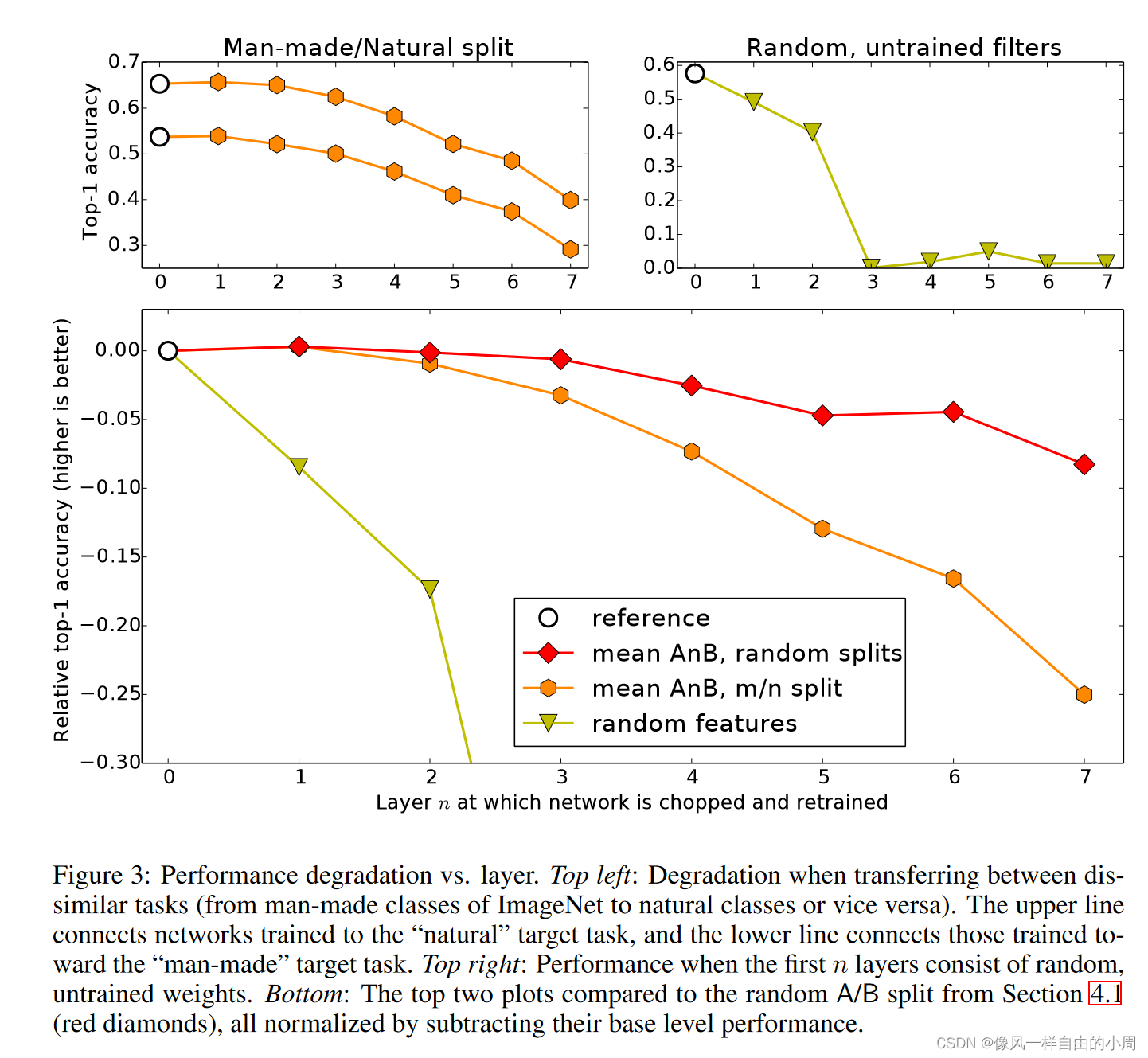
文章目录一、背景介绍二、方法介绍三、实验论证四、结论五、感想参考文献一、背景介绍 1.问题介绍: 许多在自然图像上训练的深度神经网络都表现出一个奇怪的共同现象:在第一层,它们学习类似于Gabor过滤器和color blobs的特征。这样的第一层特…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
