线性代数的本质(一)——向量空间
文章目录
- 向量空间
- 向量及其性质
- 基与维数
- 向量的坐标运算
《线性代数的本质》 - 3blue1brown
高中数学A版选修4-2 矩阵与变换
《线性代数及其应用》(第五版)
《高等代数简明教程》- 蓝以中
向量空间
In the beginning Grant created the space. And Grant said, Let there be vector: and there was vector.
向量及其性质
三维几何空间中的一个有向线段称为向量(vector)。本文统一用 a , b , c , k , λ a,b,c,k,\lambda a,b,c,k,λ 表示标量,小写黑体字母 u , v , w , a , b , x \mathbf u,\mathbf v,\mathbf w,\mathbf a,\mathbf b,\mathbf x u,v,w,a,b,x 表示向量。
向量通常定义两种运算:加法和数乘。加法遵循三角形法则(平行四边形法则),数乘被称为缩放(scaling)。运算法则如下图
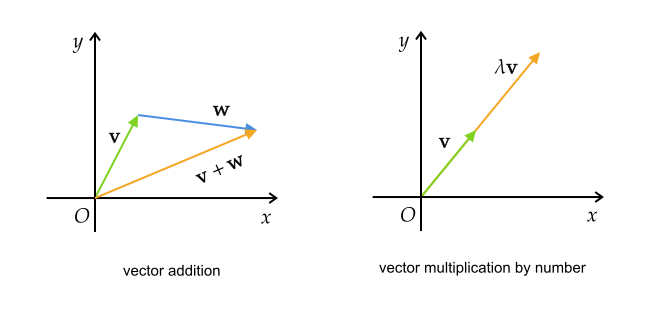
性质:根据向量的几何性质可证明向量的加法和数乘满足以下八条性质:
- 加法交换律: v + w = w + v \mathbf v+\mathbf w=\mathbf w+\mathbf v v+w=w+v
- 加法结合律: u + ( v + w ) = ( u + v ) + w \mathbf u+(\mathbf v+\mathbf w)=(\mathbf u+\mathbf v)+\mathbf w u+(v+w)=(u+v)+w
- 加法单位元: ∃ 0 ∈ V , 0 + v = v \exists 0\in V,\ 0+\mathbf v=\mathbf v ∃0∈V, 0+v=v
- 加法逆元: ∃ ( − v ) ∈ V , v + ( − v ) = 0 \exists (-\mathbf v)\in V,\ \mathbf v+(-\mathbf v)=0 ∃(−v)∈V, v+(−v)=0
- 数乘结合律: a ( b v ) = ( a b ) v a(b\mathbf v)=(ab)\mathbf v a(bv)=(ab)v
- 数乘分配律: a ( v + w ) = a v + a w a(\mathbf v+\mathbf w)=a\mathbf v+a\mathbf w a(v+w)=av+aw
- 数乘分配律: ( a + b ) v = a v + b v (a+b)\mathbf v=a\mathbf v+b\mathbf v (a+b)v=av+bv
- 数乘单位元: ∃ 1 ∈ F , 1 v = v \exists 1\in\mathbb F,\ 1\mathbf v=\mathbf v ∃1∈F, 1v=v
向量空间是三维几何空间向高维空间的推广。线性代数中,每个向量都以坐标原点为起点,那么任何一个向量就由其终点唯一确定。从而,向量和空间中的点一一对应。因此,空间也可以看成由所有向量组成的集合,并且集合中的元素可以进行加法和数乘运算。于是,便有了向量空间的抽象定义。
向量空间: 设 V V V 为 n n n 维向量的非空集合, F \mathbb F F 是一个数域,若 V V V 对于向量的加法和数乘两种运算封闭,那么称集合 V V V 为数域 F F F 上的向量空间(vector space)。所谓封闭是指
- ∀ v , w ∈ V , v + w ∈ V \forall\mathbf v,\mathbf w\in V,\ \mathbf v+\mathbf w\in V ∀v,w∈V, v+w∈V
- ∀ v ∈ V , c ∈ F , c v ∈ V \forall\mathbf v\in V, c\in F,\ c\mathbf v\in V ∀v∈V,c∈F, cv∈V
线性代数中的数域通常取全体实数,即 F = R \mathbb F=\R F=R。
例如: n n n维向量的全体生成实数域上的向量空间
R n = { x = ( x 1 , x 2 , ⋯ , x n ) ∣ x 1 , x 2 , ⋯ , x n ∈ R } \R^n=\{\mathbf x=(x_1,x_2,\cdots,x_n)\mid x_1,x_2,\cdots,x_n\in\R\} Rn={x=(x1,x2,⋯,xn)∣x1,x2,⋯,xn∈R}
子空间:设 U U U 是向量空间 V V V 的一个非空子集,如果 U U U中的线性运算封闭,则 U U U 也是向量空间,称为 V V V 的子空间。
基与维数
仿照解析几何的基本方法,建立一个坐标系,实现空间内的点与有序实数对一一对应,从而空间内的向量与有序实数对也一一对应,这样就可以用代数方法来研究向量的性质。
为方便建立空间的坐标系,先定义几个概念。
定义:取向量空间 V V V 内一个向量组 a 1 , a 2 , ⋯ , a r \mathbf a_1,\mathbf a_2,\cdots,\mathbf a_r a1,a2,⋯,ar
- 向量 x 1 a 1 + x 2 a 2 + ⋯ + x r a r x_1\mathbf a_1+x_2\mathbf a_2+\cdots+x_r\mathbf a_r x1a1+x2a2+⋯+xrar 称为向量组的一个线性组合(linear combination)
- 向量组的所有线性组合构成的向量集称为由该向量组张成的空间,记作
span { a 1 , ⋯ , a n } = { x 1 a 1 + ⋯ + x n a n ∣ x 1 , ⋯ , x n ∈ R } \text{span}\{\mathbf a_1,\cdots,\mathbf a_n\}=\{x_1\mathbf a_1+\cdots+x_n\mathbf a_n\mid x_1,\cdots,x_n\in\R\} span{a1,⋯,an}={x1a1+⋯+xnan∣x1,⋯,xn∈R}
如下图,若 u , v ∈ R 3 \mathbf u,\mathbf v\in\R^3 u,v∈R3 不共线,则 span { u , v } \text{span}\{\mathbf u,\mathbf v\} span{u,v} 是 R 3 \R^3 R3中包含 u , v \mathbf u,\mathbf v u,v 和原点的平面,图示
 3. 当且仅当系数 x 1 = x 2 = ⋯ = x r = 0 x_1=x_2=\cdots=x_r=0 x1=x2=⋯=xr=0 时,线性组合为零
3. 当且仅当系数 x 1 = x 2 = ⋯ = x r = 0 x_1=x_2=\cdots=x_r=0 x1=x2=⋯=xr=0 时,线性组合为零
x 1 a 1 + x 2 a 2 + ⋯ + x r a r = 0 x_1\mathbf a_1+x_2\mathbf a_2+\cdots+x_r\mathbf a_r=0 x1a1+x2a2+⋯+xrar=0
则称向量组线性无关(linearly independence)。反之,如果存在不全为零的数使上式成立,则称向量组线性相关(linearly dependence)。
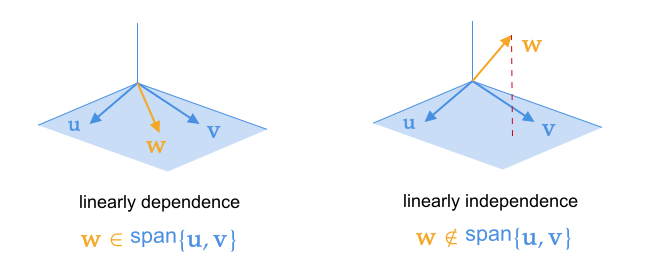
定理:若向量 v \mathbf v v 可由线性无关的向量组 a 1 , a 2 , ⋯ , a r \mathbf a_1,\mathbf a_2,\cdots,\mathbf a_r a1,a2,⋯,ar 线性表示,则表示系数是唯一的。
证明:设向量 v \mathbf v v 有两组表示系数
b = k 1 a 1 + k 2 a 2 + ⋯ + k r a r b = l 1 a 1 + l 2 a 2 + ⋯ + l r a r \mathbf b=k_1\mathbf a_1+k_2\mathbf a_2+\cdots+k_r\mathbf a_r \\ \mathbf b=l_1\mathbf a_1+l_2\mathbf a_2+\cdots+l_r\mathbf a_r b=k1a1+k2a2+⋯+krarb=l1a1+l2a2+⋯+lrar
则有
( k 1 − l 1 ) a 1 + ( k 1 − l 2 ) a 2 + ⋯ + ( k 1 − l r ) a r = 0 (k_1-l_1)\mathbf a_1+(k_1-l_2)\mathbf a_2+\cdots+(k_1-l_r)\mathbf a_r=0 (k1−l1)a1+(k1−l2)a2+⋯+(k1−lr)ar=0
因为 a 1 , a 2 , ⋯ , a r \mathbf a_1,\mathbf a_2,\cdots,\mathbf a_r a1,a2,⋯,ar 线性无关,故必有
k 1 − l 1 = k 1 − l 1 = ⋯ = k 1 − l 1 = 0 k_1-l_1=k_1-l_1=\cdots=k_1-l_1=0 k1−l1=k1−l1=⋯=k1−l1=0
即表示系数是唯一的。
接下来,我们自然想用一组线性无关的向量来张成整个向量空间。
向量空间的基:张成向量空间 V V V的一个线性无关的向量集合称为该空间的一组基(basis)。基向量组所含向量的个数,称为向量空间 V V V的维数(dimension),记为 dim V \dim V dimV。
可以证明,向量空间的任意一组基的向量个数是相等的。
单由零向量组成的向量空间 { 0 } \{0\} {0}称为零空间。零空间的维数定义为零。
基定理: n n n 维向量空间的任意 n n n 个线性无关的向量构成空间的一组基。
向量的坐标运算
向量空间选定了基向量后,空间中全体向量的集合与全体有序实数组的集合之间就建立了一一 对应的关系。
坐标:设向量组 a 1 , a 2 , ⋯ , a n \mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n a1,a2,⋯,an 是线性空间 V V V 的一组基,则空间内任一向量 v ∈ V \mathbf v\in V v∈V 都可表示为基向量的唯一线性组合
v = x 1 a 1 + x 2 a 2 + ⋯ + x n a n \mathbf v=x_1\mathbf a_1+x_2\mathbf a_2+\cdots+x_n\mathbf a_n v=x1a1+x2a2+⋯+xnan
有序数组 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn 称为向量 v \mathbf v v 在基 a 1 , a 2 , ⋯ , a n \mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n a1,a2,⋯,an 下的坐标,一般记作
[ x 1 x 2 ⋮ x n ] or ( x 1 , x 2 , ⋯ , x n ) \begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix}\quad \text{or}\quad (x_1,x_2,\cdots,x_n) x1x2⋮xn or(x1,x2,⋯,xn)
类似于三维几何空间,由 n n n个有序数构成的向量称为 n n n维向量。

例:设 v 1 = [ 3 6 2 ] , v 2 = [ − 1 0 1 ] , x = [ 3 12 7 ] \mathbf v_1=\begin{bmatrix}3\\6\\2\end{bmatrix},\mathbf v_2=\begin{bmatrix}-1\\0\\1\end{bmatrix},\mathbf x=\begin{bmatrix}3\\12\\7\end{bmatrix} v1= 362 ,v2= −101 ,x= 3127 。判断 x \mathbf x x 是否在 H = span { v 1 , v 2 } H=\text{span }\{\mathbf v_1,\mathbf v_2\} H=span {v1,v2} 中,如果是,求 x \mathbf x x 相对于基向量 B = { v 1 , v 2 } B=\{\mathbf v_1,\mathbf v_2\} B={v1,v2} 的坐标。
解:如果 x \mathbf x x 在 H = span { v 1 , v 2 } H=\text{span }\{\mathbf v_1,\mathbf v_2\} H=span {v1,v2} 中,则下列方程是有解的
c 1 [ 3 6 2 ] + c 2 [ − 1 0 1 ] = [ 3 12 7 ] c_1\begin{bmatrix}3\\6\\2\end{bmatrix}+c_2\begin{bmatrix}-1\\0\\1\end{bmatrix}=\begin{bmatrix}3\\12\\7\end{bmatrix} c1 362 +c2 −101 = 3127
如果数 c 1 , c 2 c_1,c_2 c1,c2存在,则它们是 x \mathbf x x 相对于 B B B 的坐标。由初等行变换得
[ 3 − 1 3 6 0 12 2 1 7 ] → [ 1 0 2 0 1 3 0 0 0 ] \begin{bmatrix}\begin{array}{cc:c} 3&-1&3\\6&0&12\\2&1&7 \end{array}\end{bmatrix}\to \begin{bmatrix}\begin{array}{cc:c} 1&0&2\\0&1&3\\0&0&0 \end{array}\end{bmatrix} 362−1013127 → 100010230
于是, x \mathbf x x 相对于 v 1 , v 2 \mathbf v_1,\mathbf v_2 v1,v2 的坐标
v B = [ 3 2 ] \mathbf v_B=\begin{bmatrix}3\\2\end{bmatrix} vB=[32]
有时为了区分坐标的基向量,向量 v \mathbf v v 在基 B = { b 1 , b 2 , ⋯ , b n } B=\{\mathbf b_1,\mathbf b_2,\cdots,\mathbf b_n\} B={b1,b2,⋯,bn} 下的坐标,记作 v B \mathbf v_B vB

建立了坐标之后, V V V中抽象的向量 v \mathbf v v 和 R n \R^n Rn中具体的数组 ( x 1 , x 2 , ⋯ , x n ) T (x_1,x_2,\cdots,x_n)^T (x1,x2,⋯,xn)T 实现了一一对应,并且向量的线性运算也可以表示为坐标的线性运算。
设 v , w ∈ V \mathbf v,\mathbf w\in V v,w∈V,有
v = v 1 a 1 + v 2 a 2 + ⋯ + v n a n w = w 1 a 1 + w 2 a 2 + ⋯ + w n a n \mathbf v=v_1\mathbf a_1+v_2\mathbf a_2+\cdots+v_n\mathbf a_n\\ \mathbf w=w_1\mathbf a_1+w_2\mathbf a_2+\cdots+w_n\mathbf a_n v=v1a1+v2a2+⋯+vnanw=w1a1+w2a2+⋯+wnan
向量加法运算
v + w = ( v 1 + w 1 ) a 1 + ( v 2 + w 2 ) a 2 + ⋯ + ( v n + w n ) a n \mathbf v+\mathbf w=(v_1+w_1)\mathbf a_1+(v_2+w_2)\mathbf a_2+\cdots+(v_n+w_n)\mathbf a_n v+w=(v1+w1)a1+(v2+w2)a2+⋯+(vn+wn)an
即对应的坐标运算为
[ v 1 v 2 ⋮ v n ] + [ w 1 w 2 ⋮ w n ] = [ v 1 + w 1 v 2 + w 2 ⋮ v n + w n ] \begin{bmatrix}v_1\\ v_2\\ \vdots \\ v_n\end{bmatrix}+ \begin{bmatrix}w_1\\ w_2\\ \vdots \\ w_n\end{bmatrix}= \begin{bmatrix}v_1+w_1\\ v_2+w_2\\ \vdots \\ v_n+w_n\end{bmatrix} v1v2⋮vn + w1w2⋮wn = v1+w1v2+w2⋮vn+wn
向量数乘运算
c v = ( c v 1 ) a 1 + ( c v 2 ) a 2 + ⋯ + ( c v n ) a n c\mathbf v=(cv_1)\mathbf a_1+(cv_2)\mathbf a_2+\cdots+(cv_n)\mathbf a_n cv=(cv1)a1+(cv2)a2+⋯+(cvn)an
即对应的坐标运算为
c [ v 1 v 2 ⋮ v n ] = [ c v 1 c v 2 ⋮ c v n ] c\begin{bmatrix}v_1\\ v_2\\ \vdots \\ v_n\end{bmatrix}= \begin{bmatrix}cv_1\\ cv_2\\ \vdots \\ cv_n\end{bmatrix} c v1v2⋮vn = cv1cv2⋮cvn
向量的坐标取值依托于坐标系的基向量。选取的基向量不同,其所对应的坐标值就不同。当然,基向量自身的坐标总是:
e 1 = [ 1 0 ⋮ 0 ] , e 2 = [ 0 1 ⋮ 0 ] , ⋯ , e n = [ 0 0 ⋮ 1 ] , \mathbf e_1=\begin{bmatrix}1\\0\\\vdots\\0\end{bmatrix},\quad \mathbf e_2=\begin{bmatrix}0\\1\\\vdots\\0\end{bmatrix},\quad \cdots,\quad \mathbf e_n=\begin{bmatrix}0\\0\\\vdots\\1\end{bmatrix},\quad e1= 10⋮0 ,e2= 01⋮0 ,⋯,en= 00⋮1 ,
这种坐标形式通常称为标准向量组(或单位坐标向量组)。
总之,在 n n n维向量空间 V n V_n Vn 中任取一组基,则 V n V_n Vn 中的向量与 R n \R^n Rn 中的数组之间就有一一对应的关系,且这个对应关系保持线性组合(线性运算)的一一对应。接下来我们将默认使用标准坐标系:坐标原点为 O O O,基向量组为 e 1 , e 2 , ⋯ , e n \mathbf e_1,\mathbf e_2,\cdots,\mathbf e_n e1,e2,⋯,en 。后续将对向量实体和坐标不做区分。
相关文章:

线性代数的本质(一)——向量空间
文章目录 向量空间向量及其性质基与维数向量的坐标运算 《线性代数的本质》 - 3blue1brown 高中数学A版选修4-2 矩阵与变换 《线性代数及其应用》(第五版) 《高等代数简明教程》- 蓝以中 向量空间 In the beginning Grant created the space. And Grant said, Let there be vec…...
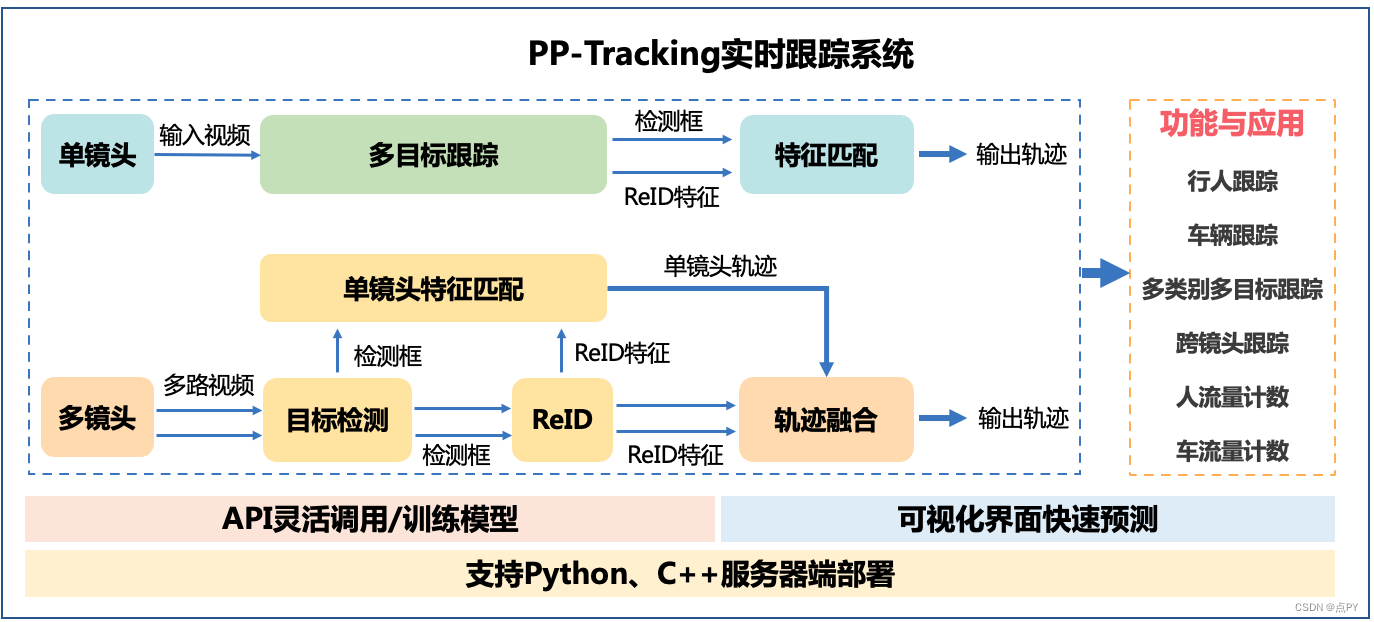
PP-Tracking之C++部署
文章目录 概要环境fastdeploy源码编译PP-Tracking源码编译使用参考概要 PP-Tracking是基于飞桨深度学习框架的业界首个开源实时跟踪系统。针对实际业务的难点痛点,PP-Tracking内置行人车辆跟踪、跨镜头跟踪、多类别跟踪、小目标跟踪及流量计数等能力与产业应用,同时提供可视…...

智慧公厕建设,要以技术为支撑、体验为目的、业务为驱动
#智慧公厕[话题]# #智慧公厕系统[话题]# #智慧公厕厂家[话题]# #智慧公厕驿站[话题]# 在数字化城市与智慧城市的大力推进下,作为社会重要的生活设施,智慧化的公共厕所的建设变得越来越重要。作为城市的基础部件之一,公厕的智慧化建设需要进行…...

通过Sealos 180秒部署一套K8S集群
通过Sealos 180秒部署一套K8S集群 一、主机准备 1.1 主机操作系统说明 序号操作系统及版本备注1CentOS7u9 1.2 主机硬件配置说明 k8s集群CPU及内存最低分别为2颗CPU、2G内存,硬盘建议为100G 需求CPU内存硬盘角色主机名值8C8G1024GBmasterk8s-master01值8C8G1024…...

如何获取美团的热门商品和服务
导语 美团是中国最大的生活服务平台之一,提供了各种各样的商品和服务,如美食、酒店、旅游、电影、娱乐等。如果你想了解美团的热门商品和服务,你可以使用爬虫技术来获取它们。本文将介绍如何使用Python和BeautifulSoup库来编写一个简单的爬虫…...
开启编程之门
自我介绍 目前已经大二了,计算机专业在读,是一个热爱编程,做事踏实专注的人。转眼间一年已经过去了,也接触编程一年了,但开始并没有对所学所想进行很好的总结和输出,这一年也有了新的很多感悟与心得&#x…...

【ES】Too many dynamic script compilations within, max: [75/5m]; 问题处理
问题原因 ElasticSearch5分钟内脚本编译的数量不能超过75个。 解决方法 PUT _cluster/settings {"persistent": {"script.max_compilations_rate": "1000/1m"} }参数可以根据自己需要定义,比如10分钟3000个,3000/10m等…...
LED智能家居灯 开关调光 台灯落地灯控制驱动 降压恒流IC AP5191
产品描述 AP5191是一款PWM工作模式,高效率、外围简单、内置功率MOS管,适用于4.5-150V输入的高精度降压LED恒流驱动芯片。输出最大功率150W,最大电流6A。AP5191可实现线性调光和PWM调光,线性调光脚有效电压范围0.55-2.6V.AP5191 工作频率可以…...
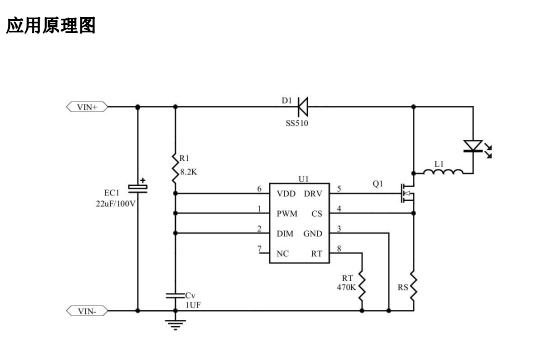
贪心算法的思路和典型例题
一、贪心算法的思想 贪心算法是一种求解问题时,总是做出在当前看来是最好的选择,不从整体最优上加以考虑的算法。 二.用贪心算法的解题策略 其基本思路是从问题的某一个初始解出发一步一步地进行,根据某个优化测度,每一步都要确保…...

演讲笔记|《一个ppt者的成长故事》
前言:本文为《说服力:工作型PPT该这样做》作者、秋叶PPT团队成员秦阳于2017年1月15日在北京望界无界空间的演讲内容要点总结。 1. 结构化思考(思考能力) 体系:挖多个坑,多个视角(构建体系 – 获…...

【八大经典排序算法】堆排序
【八大经典排序算法】堆排序 一、概述二、思路解读三、代码实现(大堆为例) 一、概述 堆排序是J.W.J. Williams于1964年提出的。他提出了一种利用堆的数据结构进行排序的算法,并将其称为堆排序。堆排序是基于选择排序的一种改进,通…...
Redis五大基本数据类型
1、字符串类型 字符串类型相当于 java 中的 String 类型。Redis 中的 String 类型以二进制方式存储,不会做任何的编码转换,因此不仅仅可以存储文本数据、整数、普通的字符串、JSON、xml文件,还可以存储图片、视频、音频。String 存储的种类虽…...

AI一点通: OpenAI whisper 在线怎么调用,怎么同时输出时间信息?
OpenAI 语音转文字 whisper API提供了两个端点,即转录和翻译,这基于我们最先进的开源大型v2 Whisper模型。它们可以用来: 将音频转录成音频所在的语言。 翻译并将音频转录成英文。 文件上传目前限制为25 MB,支持以下输入文件类型…...

OpenText EnCase Mobile Investigator 查看、分析和报告被调查手机的证据
OpenText EnCase Mobile Investigator 查看、分析和报告被调查手机的证据 全球83.72%的人口拥有智能手机 OpenText™ EnCase™ Mobile Investigator 使调查人员能够轻松分析、审查和报告与其案件相关的移动设备上的证据。 为什么选择OpenText EnCase Mobile Investigator 预算友…...
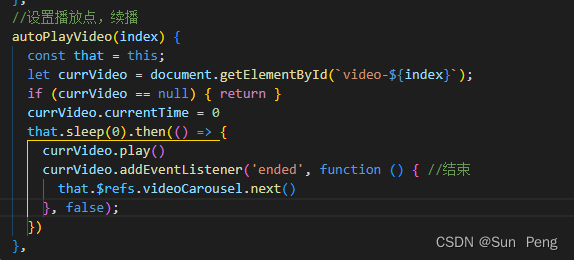
【JavaScript】video标签配置及相关事件:
文章目录 一、标签配置:二、事件:三、案例: 一、标签配置: 标签名描述src要播放的路径地址autoplay是否自动播放,默认值是false,(Boolean)loop是否循环播放,默认值是false,…...

SpringSecurity 初始化解析
文章目录 前言加载SpringSecurity配置解析配置SpringSecurity 解析器security:http 解析FilterChainProxy的注册过程创建 SpringSecurity 过滤器总结 前言 通过上文分析知道了SpringSecurity对一个请求的具体处理流程。不知道大家是否跟我一样都有几个疑问: Filte…...

ip netns网络空间使用
SNAT 源地址转发 执行ip netns exec route_br_ens192_0 iptables -nL POSTROUTING -t nat --line-numbers 输出如下: Chain POSTROUTING (policy ACCEPT) num target prot opt source destination 1 SNAT all -- 0.0.0.0/…...
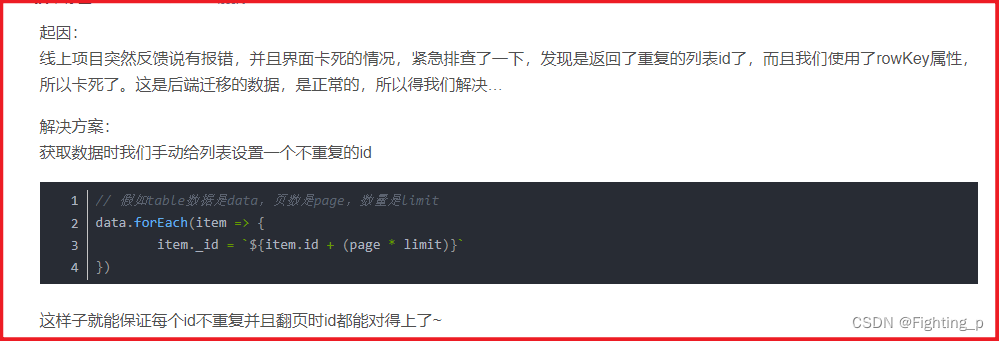
解决 Cannot read property ‘key‘ of undefined
目录 问题解决1解决2最终 问题 现场环境分页查询某些条件项查询时,分页接口获取成功但是数据不渲染,页面像是卡住了: 报错 Cannot read property key of undefined 解决1 有人说 使用的el-pagination在格式化代码的时候layout属性的参数会多加…...

「聊设计模式」之工厂方法模式(Factory Method)
🏆本文收录于《聊设计模式》专栏,专门攻坚指数级提升,助你一臂之力,早日登顶🚀,欢迎持续关注&&收藏&&订阅! 前言 设计模式是指在软件设计中,经过总结和提炼的&#…...
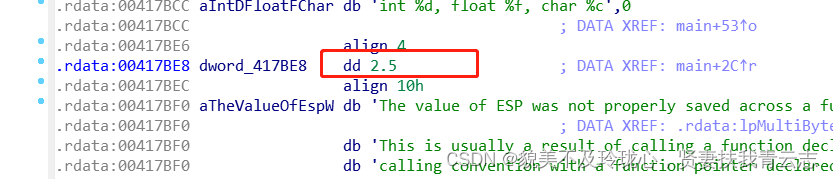
局部变量,全局变量与内存
本文会使用IDA分析局部变量,全局变量在内存的存储 目录 使用IDA分析局部变量 使用IDA分析全局变量 总结 使用IDA分析局部变量 #include <stdio.h>int main() {int nNum 1;float fNum 2.5;char ch A;printf("int %d, float %f, char %c", nNu…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...
