【python】用plotly绘制正二十面体
文章目录
- 顶点
- 棱
- 实现正二十面体
plotly 的 Python 软件包是一个开源的代码库,它基于 plot.js,而后者基于 d3.js。我们实际使用的则是一个对 plotly 进行封装的库,名叫 cufflinks,能让你更方便地使用 plotly 和 Pandas 数据表协同工作。
一言以蔽之,plotly是一款擅长交互的Python绘图库,下面就初步使用一下这个库的三维绘图功能。此前曾经用matplotlib画了正二十面体和足球:Python绘制正二十面体;画足球,这次用plotly复现一下正二十面体的绘制过程,也体验一下这两个绘图包的差异。
来绘制一个正二十面体。
顶点
正20面体的12个顶点刚好可以分为三组,每一组都是一个符合黄金分割比例的长方形,而且这三个长方形是互相正交的。
所以,想绘制一个正二十面体是比较容易的
import plotly
import plotly.express as px
import numpy as np
from itertools import product
G = (np.sqrt(5)-1)/2
def getVertex():pt2 = [(a,b) for a,b in product([1,-1], [G, -G])]pts = [(a,b,0) for a,b in pt2]pts += [(0,a,b) for a,b in pt2]pts += [(b,0,a) for a,b in pt2]return np.array(pts)xs, ys, zs = getVertex().Tfig = px.scatter_3d(x=xs, y=ys, z=zs, size=np.ones_like(xs)*0.5)
fig.show()
得到顶点

棱
接下来连接这12个顶点,由于点数较少,所以直接遍历也不至于运算量爆炸。另一方面,正二十面体边长相同,而这些相同的边连接的也必然是最近的点,所以接下来只需建立顶点之间的距离矩阵,并抽取出距离最短的线。
def getDisMat(pts):N = len(pts)dMat = np.ones([N,N])*np.inffor i in range(N):for j in range(i):dMat[i,j] = np.linalg.norm([pts[i]-pts[j]])return dMatpts = getVertex()
dMat = getDisMat(pts)
# 由于存在舍入误差,所以得到的边的数值可能不唯一
ix, jx = np.where((dMat-np.min(dMat))<0.01)
接下来,绘制正二十面体的棱
edges = []
for k in range(len(ix)):edges.append(pts[ix[k]].tolist() + [k])edges.append(pts[jx[k]].tolist() + [k])edges = np.array(edges)fig = px.line_3d(edges, x=0, y=1, z=2, color=3)
fig.show()
效果如图所示

实现正二十面体
接下来要对面上色。由于三棱成个面,所以只需得到所有三条棱的组合,只要这三条棱可以组成三角形,就能获取所有的三角面。当然,这一切的前提是,正二十面体只有30个棱,即使遍历多次,也无非27k的计算量,是完全没问题的。
def isFace(e1, e2, e3):pts = np.vstack([e1, e2, e3])pts = np.unique(pts, axis=0)return len(pts)==3edges = [pts[[i,j]] for i,j in zip(ix, jx)]
from itertools import combinations
faces = [es for es in combinations(edges, 3) if isFace(*es)]
最后得到的faces有20个元素,每个元素由3条棱组成,每条棱有两个顶点,故而可以缩减为三个顶点。
ptFace = [np.unique(np.vstack(f),axis=0) for f in faces]
ptFace = np.vstack(ptFace)
接下来绘制一下,plotly绘制三角面的逻辑是,除了需要指定三角面的三个坐标之外,还需指定三角面的顶点序号
import plotly.figure_factory as ff
simplices = np.arange(len(ptFace)).reshape(-1,3)
fig = ff.create_trisurf(x=ptFace[:,0], y=ptFace[:,1], z=ptFace[:,2],simplices=simplices)
fig.show()
效果如下

相关文章:

【python】用plotly绘制正二十面体
文章目录顶点棱实现正二十面体plotly 的 Python 软件包是一个开源的代码库,它基于 plot.js,而后者基于 d3.js。我们实际使用的则是一个对 plotly 进行封装的库,名叫 cufflinks,能让你更方便地使用 plotly 和 Pandas 数据表协同工作…...
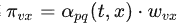
[Datawhale][CS224W]图机器学习(五)
这里写目录标题一、Deepwalk1.1 预备知识1.2 Deepwalk介绍1.3 Embedding1.4 word2Vec 词向量,词嵌入1.5 random Walk随机游走1.6 DeepWalk 核心代码Random WalkWord2vecDeepWalk应用1.7 DeepWalk优缺点二、Node2Vec2.1 图嵌入2.2 Node2Vec优化目标顶点序列采样策略2…...
Windows部署Jar包的三种方式
文章目录1、cmd命令启动2、bat脚本启动2.1 启动jar包2.2 关闭服务3、使用WinSW3.1 重命名3.2 xml配置3.3 安装服务3.4 卸载服务3.5 启动和停止服务1、cmd命令启动 这种方式比较简单,但是窗口关闭后服务也就被杀死了,命令如下 java -jar xxx.jar2、bat脚…...

【图像分类】卷积神经网络之AlexNet网络模型结构详解
写在前面: 首先感谢兄弟们的关注和订阅,让我有创作的动力,在创作过程我会尽最大能力,保证作品的质量,如果有问题,可以私信我,让我们携手共进,共创辉煌。 1. 前言 LeNet5网络模型提出之后,卷积神经网络在很长一段时间都没有长足的发展,主要有以下两个原因: 1.1 训…...

学习动漫插画的网络班排行榜
很多小伙伴不知道动漫插画培训机构哪个好,找不到靠谱的插画班,今天给大家整理了国内动漫插画培训机构排名! 一:动漫插画培训机构排名 1、轻微课(五颗星) 主打课程有日系插画、游戏原画、古风插画、动漫漫画…...
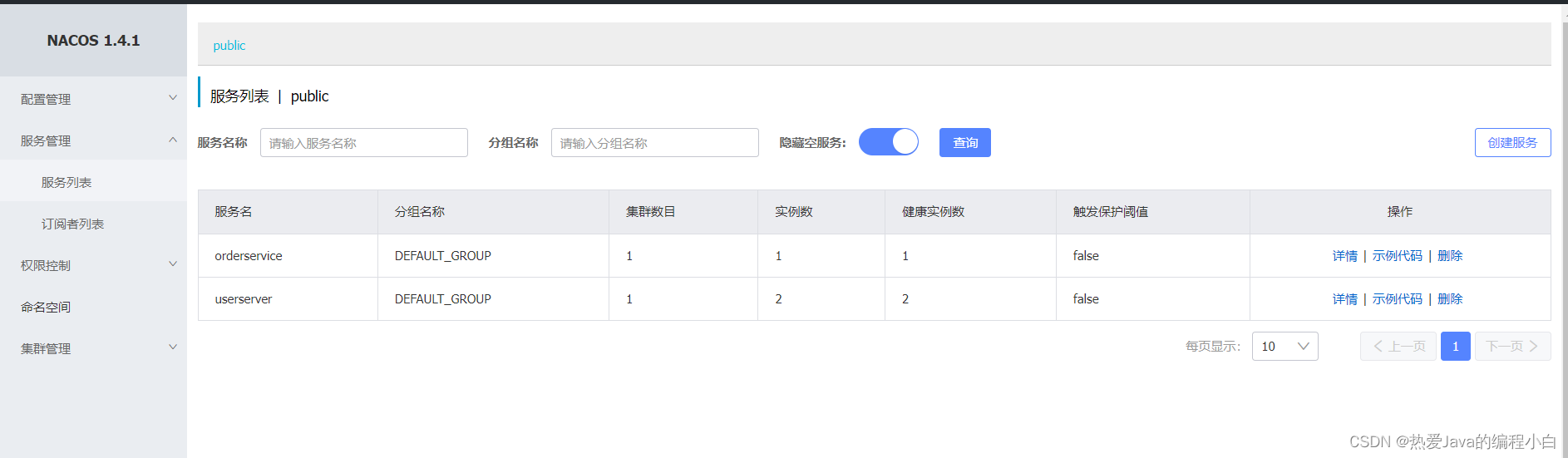
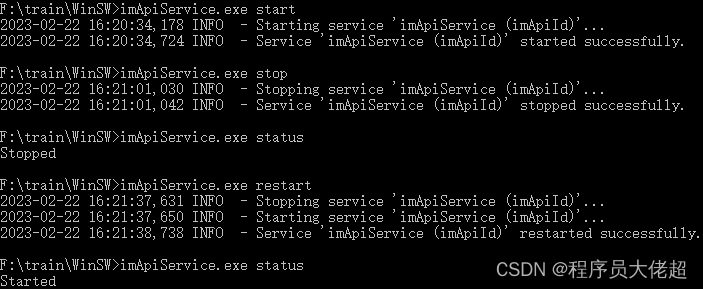
SpringCloud第五讲 Nacos注册中心-服务注册到Nacos
1.引入依赖: 在父工程中添加spring-cloud-alibaba的管理依赖 <!-- Nacos的管理依赖--><dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-alibaba-dependencies</artifactId><version…...
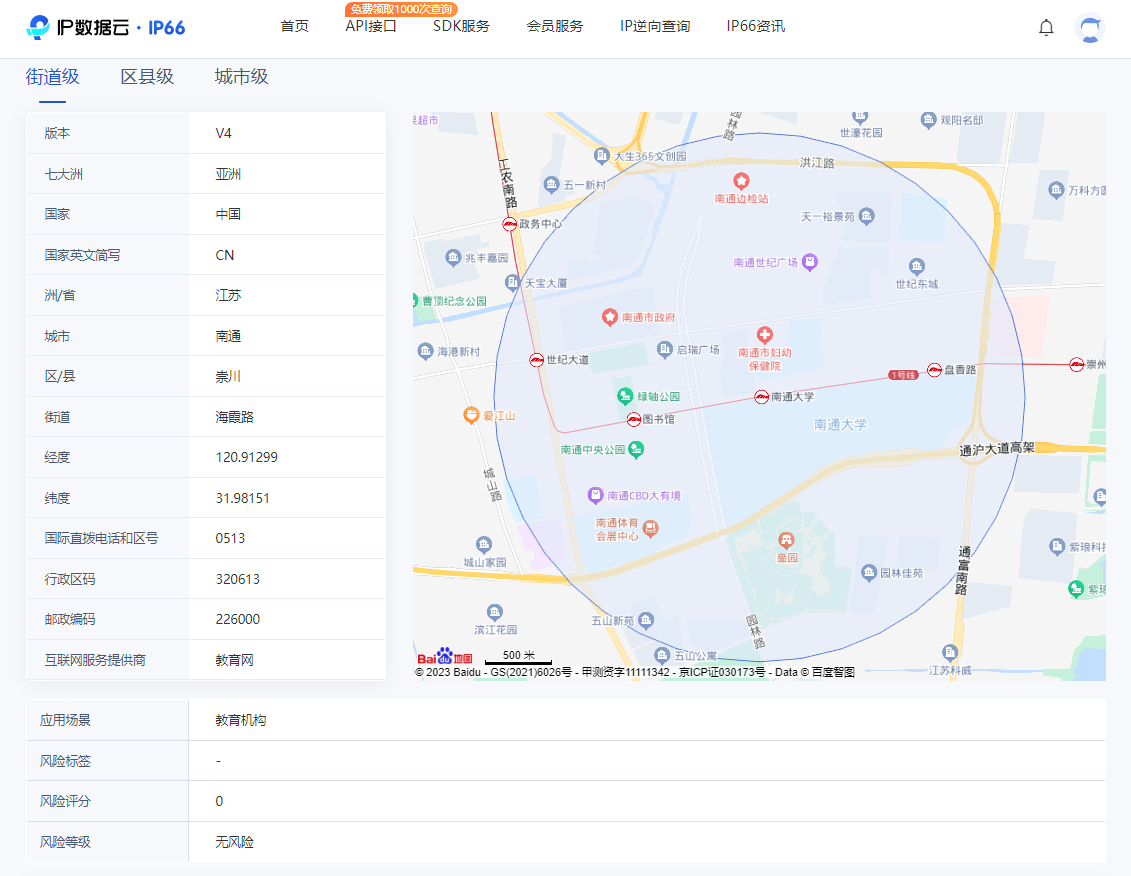
IP地理位置定位技术原理是什么
IP地理位置定位技术的原理是基于IP地址的网络通信原理和基础上的。它利用IP地址所包含的一些信息,如网络前缀和地址段,以及ISP的IP地址归属地数据库,来推测IP地址所对应的地理位置。具体来说,IP地址是由32位二进制数字组成的&…...

j-vxe-table 下拉搜索选择框数据加载过多导致前端崩溃问题
Jeeg-boot j-vxe-table 下拉搜索选择框数据加载过多导致前端崩溃问题 最近用到了Jeeg-boot j-vxe-table的组件,这组件时真J8难用,还好多BUG,想用个slot插槽也用不了,好像官方写了个基础就没怎么管了。😑 问题…...

Java国际化ResourceBundle详解
在Java开发中,ResourceBundle是一种方便地管理本地化资源的机制。它可以使得程序能够根据当前系统环境的语言和国家/地区来自动加载相应的本地化资源文件,从而避免了硬编码和减少了重复的代码。以下是使用ResourceBundle的基本步骤: 1. 准备…...

一文高端Android性能优化-总结篇
以下从几个方面来总结一下Android的性能优化:1:界面卡顿优化2:内存优化3:App启动优化界面卡顿优化Android的界面为每秒60帧,即必须在16ms内完成1帧的绘制,如果某个方法耗时过程,导致16ms内无法完…...

深入讲解CFS组调度!(上)
注:本文缩写说明 一、CFS组调度简介 1.1. 存在的原因 总结来说是希望不同分组的任务在高负载下能分配可控比例的CPU资源。为什么会有这个需求呢,比如多用户计算机系统每个用户的所有任务划分到一个分组中,A用户90个相同任务,而B…...
大数据实操项目分享:餐饮智能推荐服务在线实习项目
项目背景:在“互联网"背景下,餐饮企业的经营方式发生了很大的变革:团购和020拓宽了销售 渠道,电子点餐、店内WIFI等信息技术提升了服务水平,大数据、私人定制更好地满足了细分市场的需求等。但是与此同时…...

代码随想录day38
动态规划五部曲 确定dp数组以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 509. 斐波那契数 https://leetcode.cn/problems/fibonacci-number/ class Solution {public int fib(int n) {if(n0) return 0;if(n<3) return 1;int[] dp new int[n]…...
《计算机网络:自顶向下方法》实验5:TCP
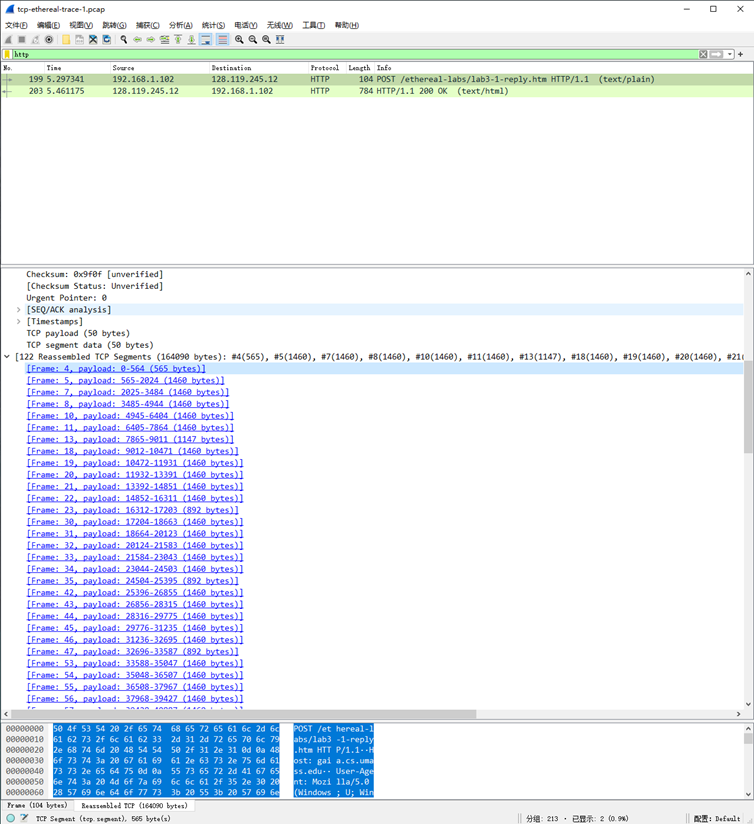
Q1 包含HTTP POST消息的TCP报文段的序号是多少?注意:为了发现POST 命令, 你需要在wireshark底部的报文内容域窗口中去查找,查找数据中包含 “POST”的段。 如图所示,由报文中的POST 和 HTTP/1.1可知,其包含HTTP POST消息; TCP报文段的序号可见TCP报文: Sequence Number:…...

【踩坑指南】Stable Diffusion 服务器端部署笔记
文章目录下载github文件配置环境ckpt文件权重下载生成图像NSFW检查(瑟图过滤)下载github文件 https://github.com/CompVis/stable-diffusion 这个网址,下载压缩包解压,也可以用git clone下载 配置环境 这一步坑最多,…...

[qiankun]-多页签缓存
[qiankun]-多页签缓存环境功能需求多页签缓存方案方案1.主服务进行html替换方案2.微服务vnode 替换方案3.每个微服务都不卸载微服务加载方式的选择微服务的路由路径选择微服务的缓存工具微服务的容器使用tab作为微服务的挂载容器使用微服务路由作为微服务的挂载容器场景描述微服…...

2|电子技术|数字电子技术基础|雨课堂习题|考前回顾
A/DD/A转化横向与阵列 相乘,竖向为或阵列 相加!功率放大电路克服交越失真,是在乙类的基础上增加两个二极管,使微导通,使三极管导通时间大于半个周期,小于一个周期,构成甲乙类工作状态。选择填空…...

vue+echarts:圆形柱状图设置角度和最大值
第020个点击查看专栏目录本示例是显示圆形的柱状图,angleAxis设置一个max, angleAxis上startAngle:90 , 将0点设置为最顶点。 文章目录示例效果示例源代码(共100行)相关资料参考专栏介绍示例效果 示例源代码…...

Linux系统安装Nginx常见报错问题
安装Nginx从nginx官网下载所需版本的nginx,http://nginx.org/下载之后,将安装包上传到linux系统指定路径解压文件,tar -zxvf nginx-1.22.1.tar.gz (此处用1.22.1版本为例)进入安装包目录,cd nginx-1.22.1执…...

按下按键之后,打印一句话------>三个按键需要实现
main.c: #include "key.h" extern void printf(const char *fmt, ...); void delay_ms(int ms){ int i,j; for(i 0; i < ms;i) for (j 0; j < 1800; j);} int main(){ //key1键盘 //EXIT控制器初始化 void PF9_exti_init(); //GICD控…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
