[Datawhale][CS224W]图机器学习(五)
这里写目录标题
- 一、Deepwalk
- 1.1 预备知识
- 1.2 Deepwalk介绍
- 1.3 Embedding
- 1.4 word2Vec 词向量,词嵌入
- 1.5 random Walk随机游走
- 1.6 DeepWalk 核心代码
- Random Walk
- Word2vec
- DeepWalk应用
- 1.7 DeepWalk优缺点
- 二、Node2Vec
- 2.1 图嵌入
- 2.2 Node2Vec
- 优化目标
- 顶点序列采样策略
- 2.3 理论上的实现
- 2.4 Node2Vec代码实现
- 学习算法
- node2vec核心代码
- node2vecWalk
- 构造采样表
- node2vec应用
- 2.5 Node2Vec与DeepWalk相比的优点与特点
- 2.6 Node2Vec的优缺点
- 参考文献
一、Deepwalk
1.1 预备知识
机器学习,深度学习基础,语言模型,word2vec
1.2 Deepwalk介绍
DeepWalk的思想类似word2vec,使用图中节点与节点的共现关系来学习节点的向量表示。那么关键的问题就是如何来描述节点与节点的共现关系,DeepWalk给出的方法是使用随机游走(RandomWalk)的方式在图中进行节点采样。
DeepwalkDeepwalkDeepwalk将graphgraphgraph的每一个节点编码为一个DDD维向量(Embedding)(无监督学习)
Embedding中隐式包含了GraphGraphGraph中的社群,连接,结构信息,可用于后续节点分类等下游任务(监督学习)

Deepwalk通过套用随机游走(Random walk generation)将图像转化为D维向量
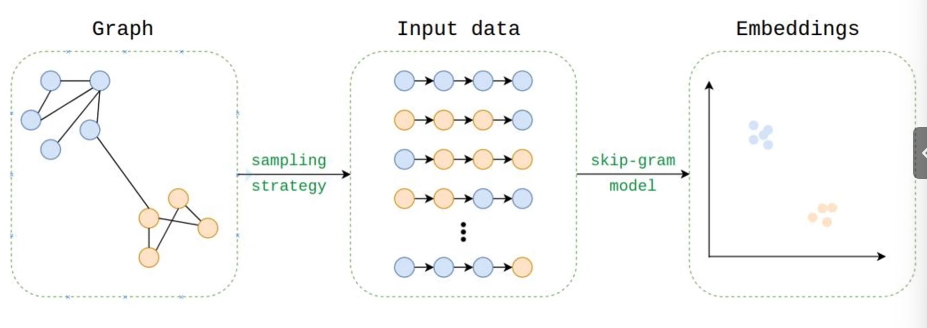
1.3 Embedding
我们需要将图转化为计算机了解的向量,所以我们需要使用embedding

1.4 word2Vec 词向量,词嵌入
word2vec通过语料库中的句子序列来描述词与词的共现关系,进而学习到词语的向量表示。
主要有两种方法
CBOW:用边缘词去预测中心词
Skip-gram:用输入的中心词去预测周围词

1.5 random Walk随机游走
RandomWalk是一种可重复访问已访问节点的深度优先遍历算法。给定当前访问起始节点,从其邻居中随机采样节点作为下一个访问节点,重复此过程,直到访问序列长度满足预设条件。
获取足够数量的节点访问序列后,使用skip-gram model 进行向量学习。

具体见[[Datawhale][CS224W]图机器学习(四)](https://blog.csdn.net/weixin_45856170/article/details/129070015)
1.6 DeepWalk 核心代码
DeepWalk算法主要包括两个步骤,第一步为随机游走采样节点序列,第二步为使用skip-gram modelword2vec学习表达向量。
①构建同构网络,从网络中的每个节点开始分别进行Random Walk 采样,得到局部相关联的训练数据; ②对采样数据进行SkipGram训练,将离散的网络节点表示成向量化,最大化节点共现,使用Hierarchical Softmax来做超大规模分类的分类器
Random Walk
我们可以通过并行的方式加速路径采样,在采用多进程进行加速时,相比于开一个进程池让每次外层循环启动一个进程,我们采用固定为每个进程分配指定数量的num_walks的方式,这样可以最大限度减少进程频繁创建与销毁的时间开销。
deepwalk_walk方法对应上一节伪代码中第6行,_simulate_walks对应伪代码中第3行开始的外层循环。最后的Parallel为多进程并行时的任务分配操作。
def deepwalk_walk(self, walk_length, start_node):walk = [start_node]while len(walk) < walk_length:cur = walk[-1]cur_nbrs = list(self.G.neighbors(cur))if len(cur_nbrs) > 0:walk.append(random.choice(cur_nbrs))else:breakreturn walkdef _simulate_walks(self, nodes, num_walks, walk_length,):walks = []for _ in range(num_walks):random.shuffle(nodes)for v in nodes: walks.append(self.deepwalk_walk(alk_length=walk_length, start_node=v))return walksresults = Parallel(n_jobs=workers, verbose=verbose, )(delayed(self._simulate_walks)(nodes, num, walk_length) for num inpartition_num(num_walks, workers))walks = list(itertools.chain(*results))
Word2vec
这里就偷个懒直接用gensim里的Word2Vec了。
from gensim.models import Word2Vec
w2v_model = Word2Vec(walks,sg=1,hs=1)
DeepWalk应用
G = nx.read_edgelist('../data/wiki/Wiki_edgelist.txt',create_using=nx.DiGraph(),nodetype=None,data=[('weight',int)])model = DeepWalk(G,walk_length=10,num_walks=80,workers=1)
model.train(window_size=5,iter=3)
embeddings = model.get_embeddings()evaluate_embeddings(embeddings)
plot_embeddings(embeddings)
1.7 DeepWalk优缺点
- 优点
- 首个将深度学习和自然语言处理的思想用于图机器学习
- 在系数标注节点分类场景下,嵌入性能卓越
- 缺点
- 均匀随机游走,没有偏向的游走方向(Node2Vec)
- 需要大量随机游走序列训练
- 基于随机游走,管中窥豹。距离较远的两个节点无法相互影响。看不到全图信息。(图神经网络)
- 无监督,仅编码图的连接信息,没有利用节点的属性特征
- 没有真正用到神经网络和深度学习
二、Node2Vec
2.1 图嵌入
将数据转化为D维连续稠密的向量,包含了原来的节点的多种信息


2.2 Node2Vec
优化目标
设 f(u)f(u)f(u)是将顶点 uuu 映射为embedding向量的映射函数,对于图中每个顶点uuu,定义 Ns(u)N_s(u)Ns(u) 为通过采样策略 SSS采样出的顶点 uuu的近邻顶点集合。
node2vec优化的目标是给定每个顶点条件下,令其近邻顶点(如何定义近邻顶点很重要)出现的概率最大。
maxf∑u∈VlogPr(Ns(U)∣f(u))max_f\sum_{u\in V}log Pr(N_s(U)|f(u))maxf∑u∈VlogPr(Ns(U)∣f(u))
为了将上述最优化问题可解,文章提出两个假设:
- 条件独立性假设
假设给定源顶点下,其近邻顶点出现的概率与近邻集合中其余顶点无关。 Pr(Ns(u)∣f(u))=∏ni∣f(u)Pr(ni∣f(u))Pr(N_s(u)|f(u))=\prod_{n_i|f(u)}Pr(n_i|f(u))Pr(Ns(u)∣f(u))=∏ni∣f(u)Pr(ni∣f(u))
- 特征空间对称性假设
这里是说一个顶点作为源顶点和作为近邻顶点的时候共享同一套embedding向量。(对比LINE中的2阶相似度,一个顶点作为源点和近邻点的时候是拥有不同的embedding向量的) 在这个假设下,上述条件概率公式可表示为 Pr(ni∣f(u))=expf(ni)⋅f(u)∑v∈Vexpf(v)⋅f(u)Pr(n_i|f(u))={expf(n_i)\cdot f(u)}\over{\sum_{v\in V}expf(v)\cdot f(u)}∑v∈Vexpf(v)⋅f(u)Pr(ni∣f(u))=expf(ni)⋅f(u)
根据以上两个假设条件,最终的目标函数表示为
由于归一化因子  的计算代价高,所以采用负采样技术优化。
的计算代价高,所以采用负采样技术优化。
顶点序列采样策略
node2vec依然采用随机游走的方式获取顶点的近邻序列,不同的是node2vec采用的是一种有偏的随机游走。
给定当前顶点 v ,访问下一个顶点 x 的概率为
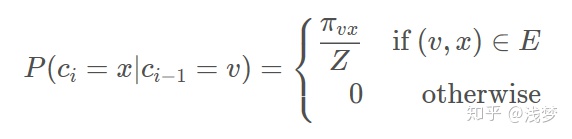
πvx\pi_{vx}πvx 是顶点 v 和顶点 x 之间的未归一化转移概率, Z 是归一化常数。
node2vec引入两个超参数 p 和 q 来控制随机游走的策略,假设当前随机游走经过边 (t,v) 到达顶点 �v设  ,ωvx\omega_{vx}ωvx 是顶点 v 和 x 之间的边权,
,ωvx\omega_{vx}ωvx 是顶点 v 和 x 之间的边权,

dtxd_{tx}dtx为顶点 t 和顶点 x 之间的最短路径距离。
下面讨论超参数 p 和 q 对游走策略的影响
- Return parameter,p
参数p控制重复访问刚刚访问过的顶点的概率。 注意到p仅作用于 dtxd_{tx}dtx=0 的情况,而dtxd_{tx}dtx=0 表示顶点 x 就是访问当前顶点 v 之前刚刚访问过的顶点。 那么若 p 较高,则访问刚刚访问过的顶点的概率会变低,反之变高。
- In-out papameter,q
q 控制着游走是向外还是向内,若 q>1 ,随机游走倾向于访问和 t 接近的顶点(偏向BFS)。若 q<1 ,倾向于访问远离 t 的顶点(偏向DFS)。
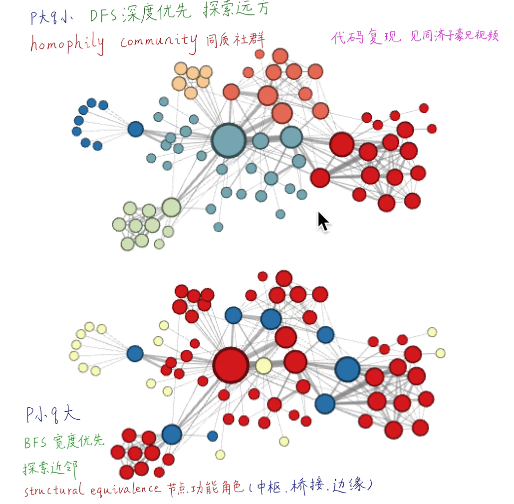
下面的图描述的是当从 t 访问到 v 时,决定下一个访问顶点时每个顶点对应的 α\alphaα 。
设定p,q进行有偏随机游走

q节点小时更愿意进行BFS,p节点小时更愿意进行DFS
2.3 理论上的实现

2.4 Node2Vec代码实现
学习算法
采样完顶点序列后,剩下的步骤就和deepwalk一样了,用word2vec去学习顶点的embedding向量。 值得注意的是node2vecWalk中不再是随机抽取邻接点,而是按概率抽取,node2vec采用了Alias算法进行顶点采样。
Alias Method:时间复杂度O(1)的离散采样方法125 赞同 · 23 评论文章
node2vec核心代码

node2vecWalk
通过上面的伪代码可以看到,node2vec和deepwalk非常类似,主要区别在于顶点序列的采样策略不同,所以这里我们主要关注node2vecWalk的实现。
由于采样时需要考虑前面2步访问过的顶点,所以当访问序列中只有1个顶点时,直接使用当前顶点和邻居顶点之间的边权作为采样依据。 当序列多余2个顶点时,使用文章提到的有偏采样。
def node2vec_walk(self, walk_length, start_node):G = self.G alias_nodes = self.alias_nodes alias_edges = self.alias_edgeswalk = [start_node]while len(walk) < walk_length: cur = walk[-1] cur_nbrs = list(G.neighbors(cur)) if len(cur_nbrs) > 0: if len(walk) == 1: walk.append(cur_nbrs[alias_sample(alias_nodes[cur][0], alias_nodes[cur][1])]) else: prev = walk[-2] edge = (prev, cur) next_node = cur_nbrs[alias_sample(alias_edges[edge][0],alias_edges[edge][1])] walk.append(next_node) else: breakreturn walk
构造采样表
preprocess_transition_probs分别生成alias_nodes和alias_edges,alias_nodes存储着在每个顶点时决定下一次访问其邻接点时需要的alias表(不考虑当前顶点之前访问的顶点)。alias_edges存储着在前一个访问顶点为 t ,当前顶点为 v 时决定下一次访问哪个邻接点时需要的alias表。
get_alias_edge方法返回的是在上一次访问顶点 t ,当前访问顶点为 v 时到下一个顶点 x 的未归一化转移概率 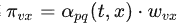
def get_alias_edge(self, t, v):G = self.G p = self.p q = self.qunnormalized_probs = [] for x in G.neighbors(v): weight = G[v][x].get('weight', 1.0)# w_vx if x == t:# d_tx == 0 unnormalized_probs.append(weight/p) elif G.has_edge(x, t):# d_tx == 1 unnormalized_probs.append(weight) else:# d_tx == 2 unnormalized_probs.append(weight/q) norm_const = sum(unnormalized_probs) normalized_probs = [float(u_prob)/norm_const for u_prob in unnormalized_probs]return create_alias_table(normalized_probs)def preprocess_transition_probs(self):G = self.Galias_nodes = {} for node in G.nodes(): unnormalized_probs = [G[node][nbr].get('weight', 1.0) for nbr in G.neighbors(node)] norm_const = sum(unnormalized_probs) normalized_probs = [float(u_prob)/norm_const for u_prob in unnormalized_probs] alias_nodes[node] = create_alias_table(normalized_probs)alias_edges = {}for edge in G.edges(): alias_edges[edge] = self.get_alias_edge(edge[0], edge[1])self.alias_nodes = alias_nodes self.alias_edges = alias_edgesreturn
node2vec应用
使用node2vec在wiki数据集上进行节点分类任务和可视化任务。 wiki数据集包含 2,405 个网页和17,981条网页之间的链接关系,以及每个网页的所属类别。 通过简单的超参搜索,这里使用p=0.25,q=4的设置。
G = nx.read_edgelist('../data/wiki/Wiki_edgelist.txt',create_using=nx.DiGraph(),nodetype=None,data=[('weight',int)])model = Node2Vec(G,walk_length=10,num_walks=80,p=0.25,q=4,workers=1)
model.train(window_size=5,iter=3)
embeddings = model.get_embeddings()evaluate_embeddings(embeddings)
plot_embeddings(embeddings)
2.5 Node2Vec与DeepWalk相比的优点与特点
- 优点
- Node2Vec解决图嵌入问题,将图中的每个节点映射为一个向量(嵌入)
- 向量(嵌入)包含了节点的语义信息(相邻社群和功能角色)
- 语义相似的节点,向量(嵌入)的距离也近。
- 向量(嵌入)用于后续的分类,聚类,link Predictin,推荐等任务。
- 特点
- 在DeepWalk完全随机游走的基础上,Node2Vec增加p,q参数,实现有偏随机游走。不同的p,q组合,对应了不同的探索范围和节点语义。
- DFS深度优先探索,相邻的节点,向量(嵌入)距离相近
- BFS广度优先探索,相同功能角色的节点,向量(嵌入)距离相近。
- DeepWalk时Node2Vec在p=1,q=1的特例
2.6 Node2Vec的优缺点
- 优点
- 首次通过调节p,q值,实现了有偏随机游走,探索节点社群,功能等不同属性
- 首次将节点分类用于Link Prediction
- 可解释性,可扩展性好,性能卓越
- 缺点
- 需要大量随机游走序列训练
- 距离较远的两个界定啊无法直接相互影响。看不到全图信息。(图神经网络)
- 无监督,仅编码图的连接信息,没有利用节点的属性特征(图卷积)
- 没有真正用到神经网络和深度学习
参考文献
[1] 斯坦福CS224W图机器学习、图神经网络、知识图谱【同济子豪兄】
[2] 【Graph Embedding】DeepWalk:算法原理,实现和应用
[3] 【Graph Embedding】node2vec:算法原理,实现和应用
相关文章:
[Datawhale][CS224W]图机器学习(五)
这里写目录标题一、Deepwalk1.1 预备知识1.2 Deepwalk介绍1.3 Embedding1.4 word2Vec 词向量,词嵌入1.5 random Walk随机游走1.6 DeepWalk 核心代码Random WalkWord2vecDeepWalk应用1.7 DeepWalk优缺点二、Node2Vec2.1 图嵌入2.2 Node2Vec优化目标顶点序列采样策略2…...
Windows部署Jar包的三种方式
文章目录1、cmd命令启动2、bat脚本启动2.1 启动jar包2.2 关闭服务3、使用WinSW3.1 重命名3.2 xml配置3.3 安装服务3.4 卸载服务3.5 启动和停止服务1、cmd命令启动 这种方式比较简单,但是窗口关闭后服务也就被杀死了,命令如下 java -jar xxx.jar2、bat脚…...

【图像分类】卷积神经网络之AlexNet网络模型结构详解
写在前面: 首先感谢兄弟们的关注和订阅,让我有创作的动力,在创作过程我会尽最大能力,保证作品的质量,如果有问题,可以私信我,让我们携手共进,共创辉煌。 1. 前言 LeNet5网络模型提出之后,卷积神经网络在很长一段时间都没有长足的发展,主要有以下两个原因: 1.1 训…...

学习动漫插画的网络班排行榜
很多小伙伴不知道动漫插画培训机构哪个好,找不到靠谱的插画班,今天给大家整理了国内动漫插画培训机构排名! 一:动漫插画培训机构排名 1、轻微课(五颗星) 主打课程有日系插画、游戏原画、古风插画、动漫漫画…...
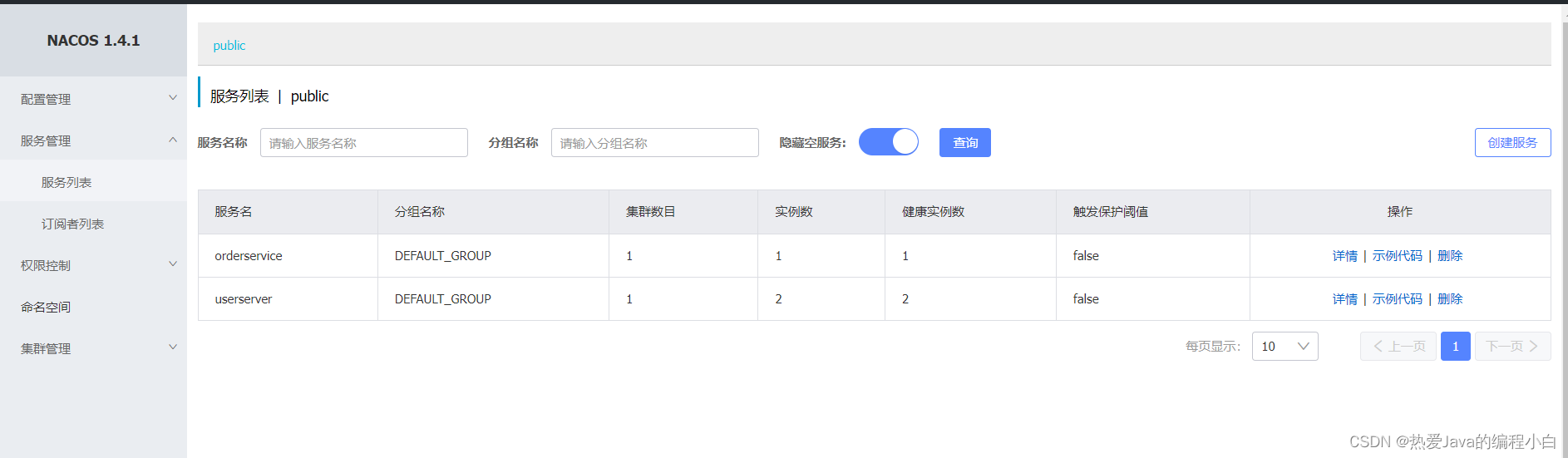
SpringCloud第五讲 Nacos注册中心-服务注册到Nacos
1.引入依赖: 在父工程中添加spring-cloud-alibaba的管理依赖 <!-- Nacos的管理依赖--><dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-alibaba-dependencies</artifactId><version…...
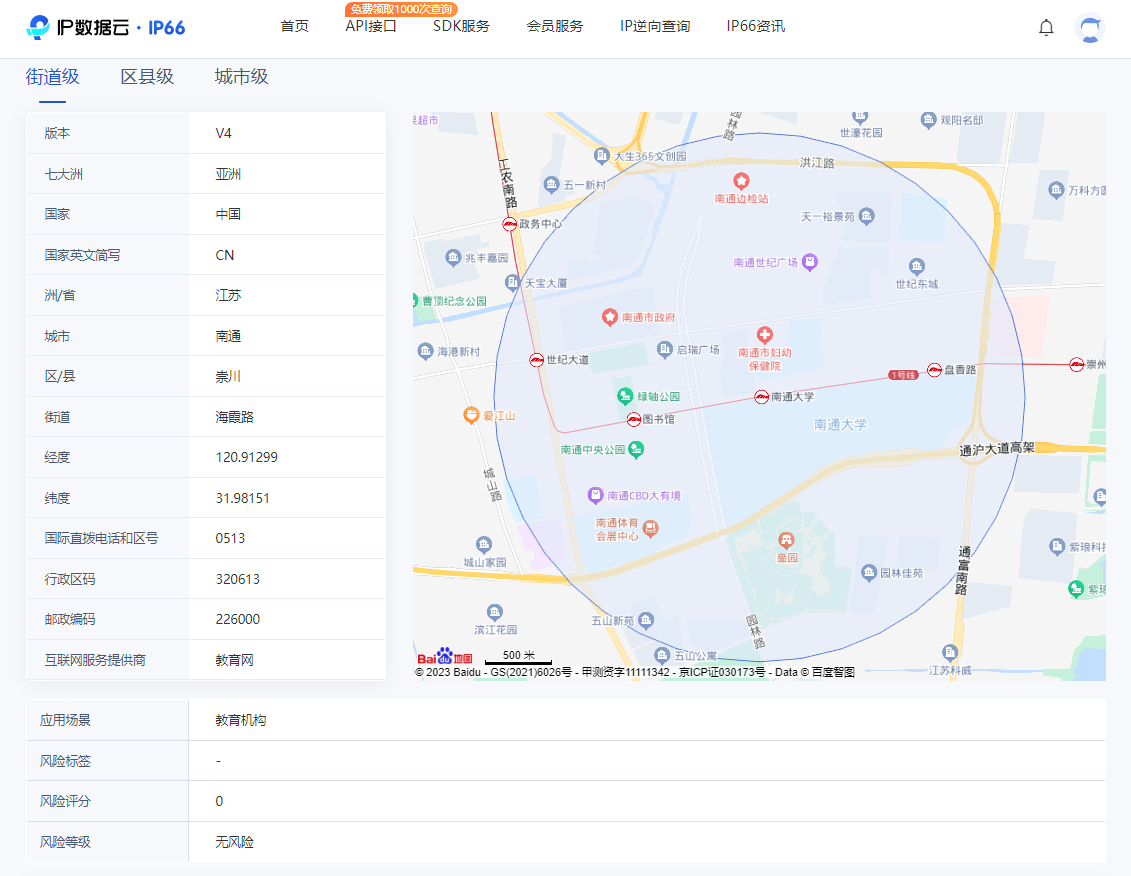
IP地理位置定位技术原理是什么
IP地理位置定位技术的原理是基于IP地址的网络通信原理和基础上的。它利用IP地址所包含的一些信息,如网络前缀和地址段,以及ISP的IP地址归属地数据库,来推测IP地址所对应的地理位置。具体来说,IP地址是由32位二进制数字组成的&…...

j-vxe-table 下拉搜索选择框数据加载过多导致前端崩溃问题
Jeeg-boot j-vxe-table 下拉搜索选择框数据加载过多导致前端崩溃问题 最近用到了Jeeg-boot j-vxe-table的组件,这组件时真J8难用,还好多BUG,想用个slot插槽也用不了,好像官方写了个基础就没怎么管了。😑 问题…...

Java国际化ResourceBundle详解
在Java开发中,ResourceBundle是一种方便地管理本地化资源的机制。它可以使得程序能够根据当前系统环境的语言和国家/地区来自动加载相应的本地化资源文件,从而避免了硬编码和减少了重复的代码。以下是使用ResourceBundle的基本步骤: 1. 准备…...

一文高端Android性能优化-总结篇
以下从几个方面来总结一下Android的性能优化:1:界面卡顿优化2:内存优化3:App启动优化界面卡顿优化Android的界面为每秒60帧,即必须在16ms内完成1帧的绘制,如果某个方法耗时过程,导致16ms内无法完…...

深入讲解CFS组调度!(上)
注:本文缩写说明 一、CFS组调度简介 1.1. 存在的原因 总结来说是希望不同分组的任务在高负载下能分配可控比例的CPU资源。为什么会有这个需求呢,比如多用户计算机系统每个用户的所有任务划分到一个分组中,A用户90个相同任务,而B…...
大数据实操项目分享:餐饮智能推荐服务在线实习项目
项目背景:在“互联网"背景下,餐饮企业的经营方式发生了很大的变革:团购和020拓宽了销售 渠道,电子点餐、店内WIFI等信息技术提升了服务水平,大数据、私人定制更好地满足了细分市场的需求等。但是与此同时…...

代码随想录day38
动态规划五部曲 确定dp数组以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 509. 斐波那契数 https://leetcode.cn/problems/fibonacci-number/ class Solution {public int fib(int n) {if(n0) return 0;if(n<3) return 1;int[] dp new int[n]…...
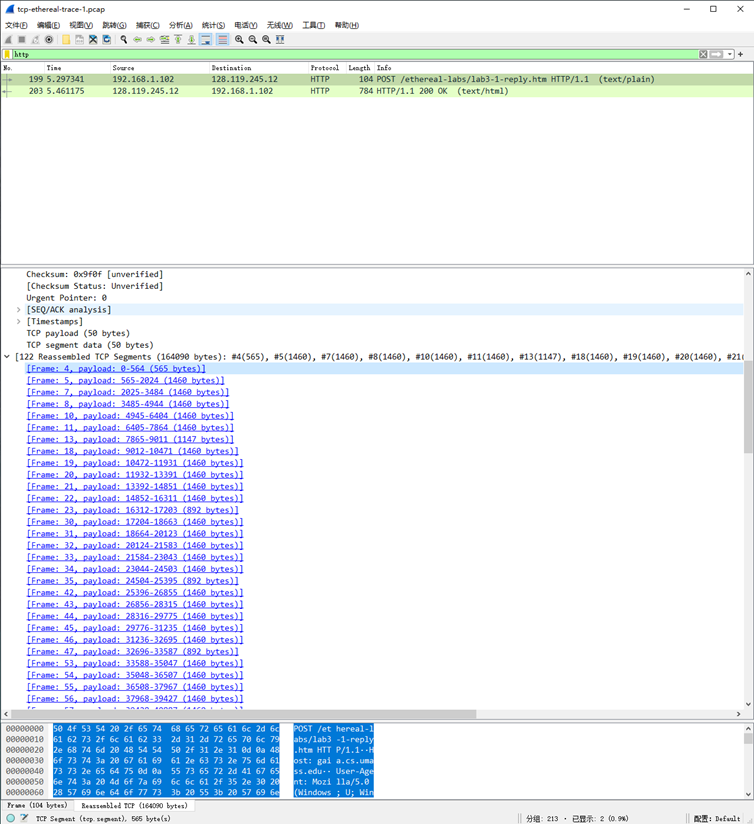
《计算机网络:自顶向下方法》实验5:TCP
Q1 包含HTTP POST消息的TCP报文段的序号是多少?注意:为了发现POST 命令, 你需要在wireshark底部的报文内容域窗口中去查找,查找数据中包含 “POST”的段。 如图所示,由报文中的POST 和 HTTP/1.1可知,其包含HTTP POST消息; TCP报文段的序号可见TCP报文: Sequence Number:…...

【踩坑指南】Stable Diffusion 服务器端部署笔记
文章目录下载github文件配置环境ckpt文件权重下载生成图像NSFW检查(瑟图过滤)下载github文件 https://github.com/CompVis/stable-diffusion 这个网址,下载压缩包解压,也可以用git clone下载 配置环境 这一步坑最多,…...

[qiankun]-多页签缓存
[qiankun]-多页签缓存环境功能需求多页签缓存方案方案1.主服务进行html替换方案2.微服务vnode 替换方案3.每个微服务都不卸载微服务加载方式的选择微服务的路由路径选择微服务的缓存工具微服务的容器使用tab作为微服务的挂载容器使用微服务路由作为微服务的挂载容器场景描述微服…...

2|电子技术|数字电子技术基础|雨课堂习题|考前回顾
A/DD/A转化横向与阵列 相乘,竖向为或阵列 相加!功率放大电路克服交越失真,是在乙类的基础上增加两个二极管,使微导通,使三极管导通时间大于半个周期,小于一个周期,构成甲乙类工作状态。选择填空…...

vue+echarts:圆形柱状图设置角度和最大值
第020个点击查看专栏目录本示例是显示圆形的柱状图,angleAxis设置一个max, angleAxis上startAngle:90 , 将0点设置为最顶点。 文章目录示例效果示例源代码(共100行)相关资料参考专栏介绍示例效果 示例源代码…...

Linux系统安装Nginx常见报错问题
安装Nginx从nginx官网下载所需版本的nginx,http://nginx.org/下载之后,将安装包上传到linux系统指定路径解压文件,tar -zxvf nginx-1.22.1.tar.gz (此处用1.22.1版本为例)进入安装包目录,cd nginx-1.22.1执…...

按下按键之后,打印一句话------>三个按键需要实现
main.c: #include "key.h" extern void printf(const char *fmt, ...); void delay_ms(int ms){ int i,j; for(i 0; i < ms;i) for (j 0; j < 1800; j);} int main(){ //key1键盘 //EXIT控制器初始化 void PF9_exti_init(); //GICD控…...

Mac配置VScode
Mac配置VScode 常用技巧 命令调色板 根据您当前的上下文访问所有可用的命令。 键盘快捷键:⇧⌘P 快速打开 快速打开文件。 键盘快捷键:⌘P **提示:**类型?查看命令建议。 在最近打开的文件夹和工作区之间导航 最近打开 键盘快捷…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...
