OLED透明屏交互技术:开创未来科技的新篇章
OLED透明屏交互技术作为一项前沿的科技创新,正在以其高透明度、触摸和手势交互等特点,引领着未来科技的发展。
不仅在智能手机、可穿戴设备和汽车行业有着广泛应用,还在广告和展示领域展现出巨大的潜力。

那么,尼伽在这篇文章中将深入探讨OLED透明屏交互技术的优势和应用前景,并结合具体数据、报告和行业动态,提升可信度和说服力。
一、OLED透明屏交互技术的特点和优势
OLED透明屏交互技术以其独特的特点和优势成为未来科技的焦点。
首先,它具有高透明度,能够实现透明度达到70%以上,让用户能够透过屏幕看到背后的景物。
其次,OLED透明屏能够提供高质量的图像和视频显示效果,为用户带来更加清晰、逼真的视觉体验。
此外,触摸和手势交互使得用户操作更加直观和自然,提供了更好的用户体验。
二、OLED透明屏交互技术的应用前景
智能手机和可穿戴设备:根据行业报告,预计到2025年,全球智能手机和可穿戴设备市场将达到数千亿美元规模。
OLED透明屏交互技术能够为这些设备提供更加直观和便捷的操作方式,从而提升用户体验和品牌竞争力。
汽车行业:根据统计数据,全球汽车市场规模逐年增长,2025年有望达到2.5万亿美元。
OLED透明屏交互技术可以应用于车载娱乐系统、导航系统和仪表盘等,提供更好的用户体验和驾驶安全性。
广告和展示领域:根据市场研究,全球广告和展示市场规模预计将超过6000亿美元。
OLED透明屏交互技术能够结合触摸和手势交互,吸引更多目光,并提升用户参与度,为广告和展示带来更好的效果。
三、具体数据、报告和行业动态的支持
根据Gartner的报告,全球智能手机销量在2020年达到了14.5亿部,相比2019年的13.8亿部增长了4.8%。
这显示了智能手机市场的持续增长趋势,为OLED透明屏交互技术的应用提供了广阔的市场基础。
根据IHS Markit的数据,截至2021年,全球可穿戴设备市场规模已经达到了5400万台,相比2020年的4100万台增长了31%。
这表明可穿戴设备市场的蓬勃发展,为OLED透明屏交互技术的应用提供了良好的机遇。
根据Deloitte的报告,全球汽车行业正在经历数字化转型,预计到2025年,全球数字化汽车市场规模将达到5000亿美元。
OLED透明屏交互技术作为数字化汽车的关键技术之一,将在汽车行业中扮演重要角色。
根据Statista的数据,全球广告支出在2021年达到了6400亿美元,预计到2025年将超过7000亿美元。
OLED透明屏交互技术的创新应用将带来更多的广告投放和展示机会,为广告行业带来巨大的潜力。
综上所述,OLED透明屏交互技术以其独特的特点和优势,正引领着未来科技的发展。
在智能手机、可穿戴设备、汽车行业以及广告和展示领域中,OLED透明屏交互技术都有着广阔的应用前景。
通过具体的数据、报告和行业动态的支持,我们可以看到这项技术的巨大潜力和市场机遇。
选择OLED透明屏交互技术,将使您的产品和服务在竞争激烈的市场中脱颖而出,开创未来科技的新篇章。
【此文由“尼伽OLED透明屏技术部门”原创,转载需备注来源和出处】
相关文章:

OLED透明屏交互技术:开创未来科技的新篇章
OLED透明屏交互技术作为一项前沿的科技创新,正在以其高透明度、触摸和手势交互等特点,引领着未来科技的发展。 不仅在智能手机、可穿戴设备和汽车行业有着广泛应用,还在广告和展示领域展现出巨大的潜力。 那么,尼伽在这篇文章中将…...

揭秘Spring Boot内嵌Tomcat原理
tomcat 介绍 tomcat 是 web容器(servlet 容器),不管请求是访问静态资源HTML、JSP还是java接口,对tomcat而言,都是通过servlet访问: 访问静态资源,tomcat 会交由一个叫做DefaultServlet的类来处…...
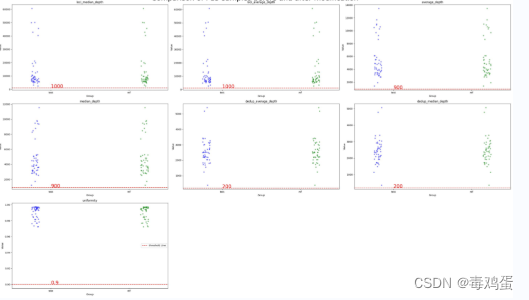
分类散点图 stripplot() 加辅助线axhline() 多图合一
分类散点图 stripplot 加辅助线axhline 多图合一 效果图代码 画图没有什么可说的,直接上图 效果图 代码 # 绘制图, 查看是否数值在阈值上 plt.figure(figsize(30, 18)) n 0 for header, value_list in info_dict.items():ref_value_list ref_info_dic…...
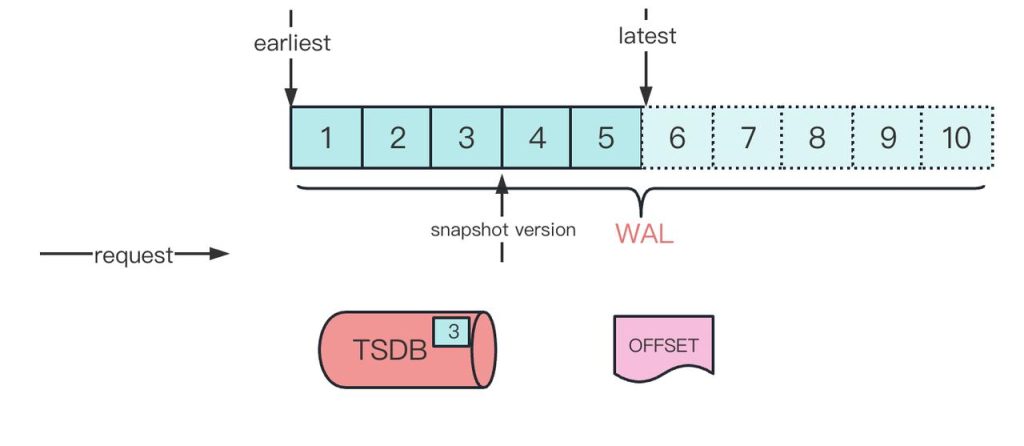
一文告诉你为什么时序场景下 TDengine 数据订阅比 Kafka 好
在 TDengine 3.0 中,我们对流式计算、数据订阅功能都进行了再升级,帮助用户极大简化了数据架构的复杂程度,降低整体运维成本。TDengine 提供的类似消息队列产品的数据订阅、消费接口,本质上是为了帮助应用实时获取写入 TDengine 的…...
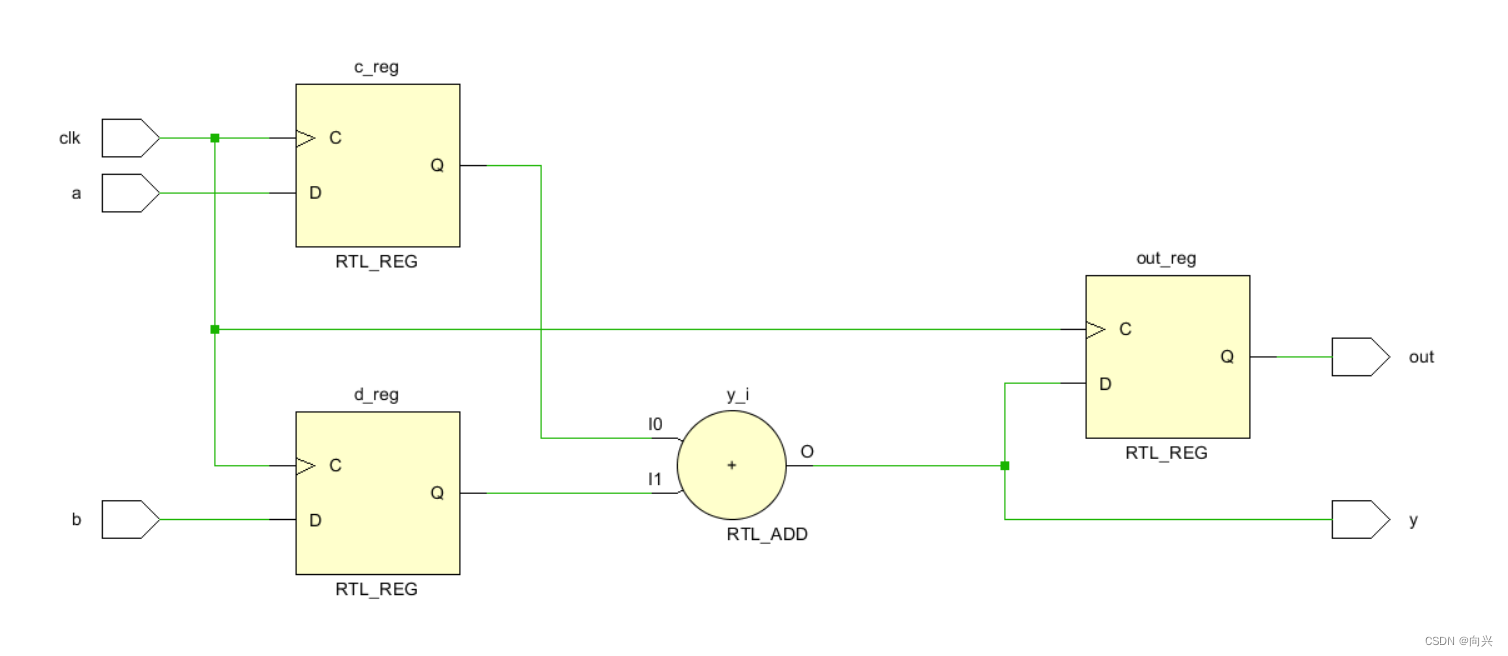
reg与wire的用法,证明reg可以在右边,wire型在左边,来作组合逻辑处理。
reg与wire的用法,证明reg可以在右边,wire型在左边,来作组合逻辑处理。 1,RTL2,生成的原理图 1,RTL 参考文献: 1,verilog 中 wire 和reg 的使用 2,解决一个assign问题&…...
Studio One6.2简体中文免费最新版本宿主软件
对于一些有创作需求的朋友来说,为自己写的歌制作伴奏是很平常的。今天要和大家分享的就是自己写的歌怎么做伴奏,自己做伴奏的软件有哪些。Studio One是宿主软件界的一个后起之秀,推出的时间不久,但是受到了大量音乐制作人的推崇。…...
算法刷题 week2
目录 week21. 二维数组中的查找题目题解(单调性扫描) O(nm) 2.替换空格题目题解(线性扫描) O(n)(双指针扫描) O(n) 3.从尾到头打印链表题目题解(遍历链表) O(n) week2 1. 二维数组中的查找 题目 题解 (单调性扫描) O(nm) 核心在于发现每个子矩阵右上角的数的性质࿱…...

子网的划分
强化计算机网络发现王道没有这一块的内容,导致做题稀里糊涂。于是个人调研补充。 子网划分是将一个大型IP网络划分成更小的子网,以实现更有效的网络管理和资源分配。 原因: 提高网络性能:子网划分可以减少广播域的大小ÿ…...

Docker安装与卸载
Docker安装与卸载 安装 yum install -y yum-utils \device-mapper-persistent-data \lvm2 --skip-broken更新本地镜像源 打开终端或 SSH 连接到 Rocky Linux 的服务器。 进入 /etc/yum.repos.d/ 目录,该目录包含 Rocky Linux 的 yum 配置文件。 cd /etc/yum.repo…...
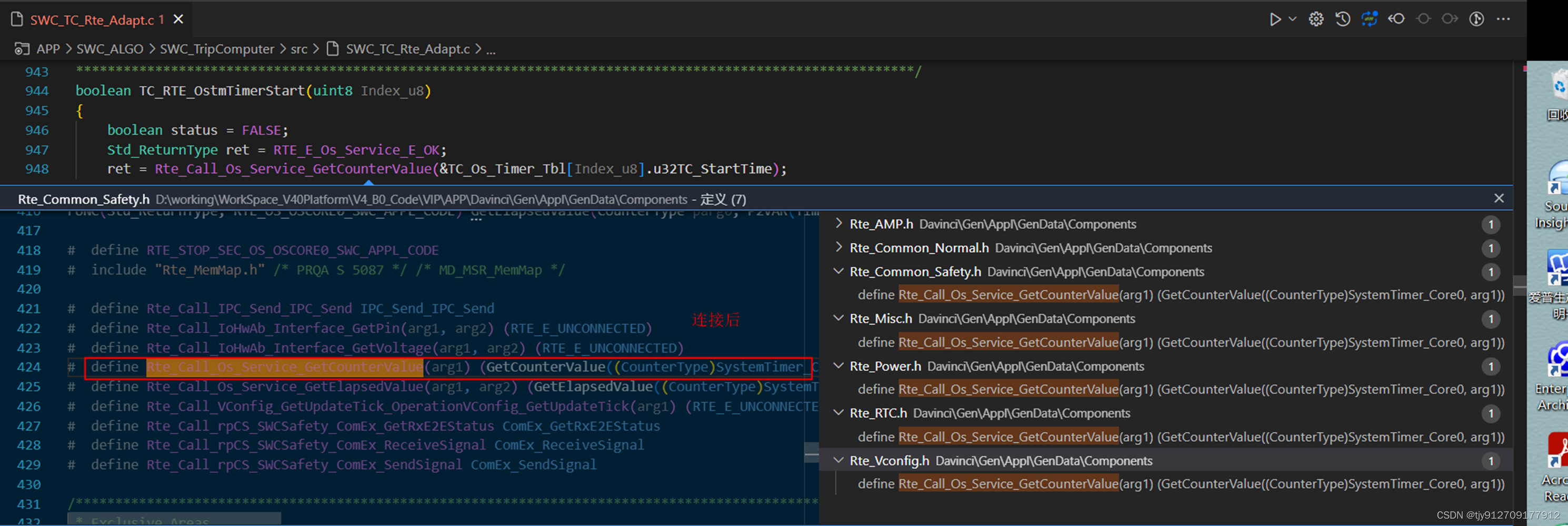
【Davinci开发】:开发过程问题记录及总结
开发过程问题总结 1、SWC访问系统OS Timer返回值异常a、代码发现,RTE接口为未连接状态b、连接后,仍然有问题,单步调试,发现没有访问权限当新平台基于之前平台的代码而延续开发时(应用代码相同,但是芯片已经更换),记录开发过程中遇所到的问题,单步调试,逐一排查。 1、…...
数据结构——排序算法——冒泡排序
冒泡排序1 void swap(vector<int> arr, int i, int j) {int temp arr[i];arr[i] arr[j];arr[j] temp;}void bubbleSort1(vector<int> arr) {for (int i 0; i < arr.size() - 1; i){for (int j 0; j < arr.size() - 1 - i; j){if (arr[j] > arr[j 1…...

vscode使用
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 前言 提示:这里可以添加本文要记录的大概内容: 例如:…...

python经典百题之求前!的和
题目:求12!3!…20!的和 方法一: 使用for循环和阶乘函数计算每项的值,再将每项的值累加起来。 def factorial(n):if n 0:return 1else:return n * factorial(n-1)sum 0 for i in range(1, 21):sum factorial(i) * iprint(sum)优点&#…...
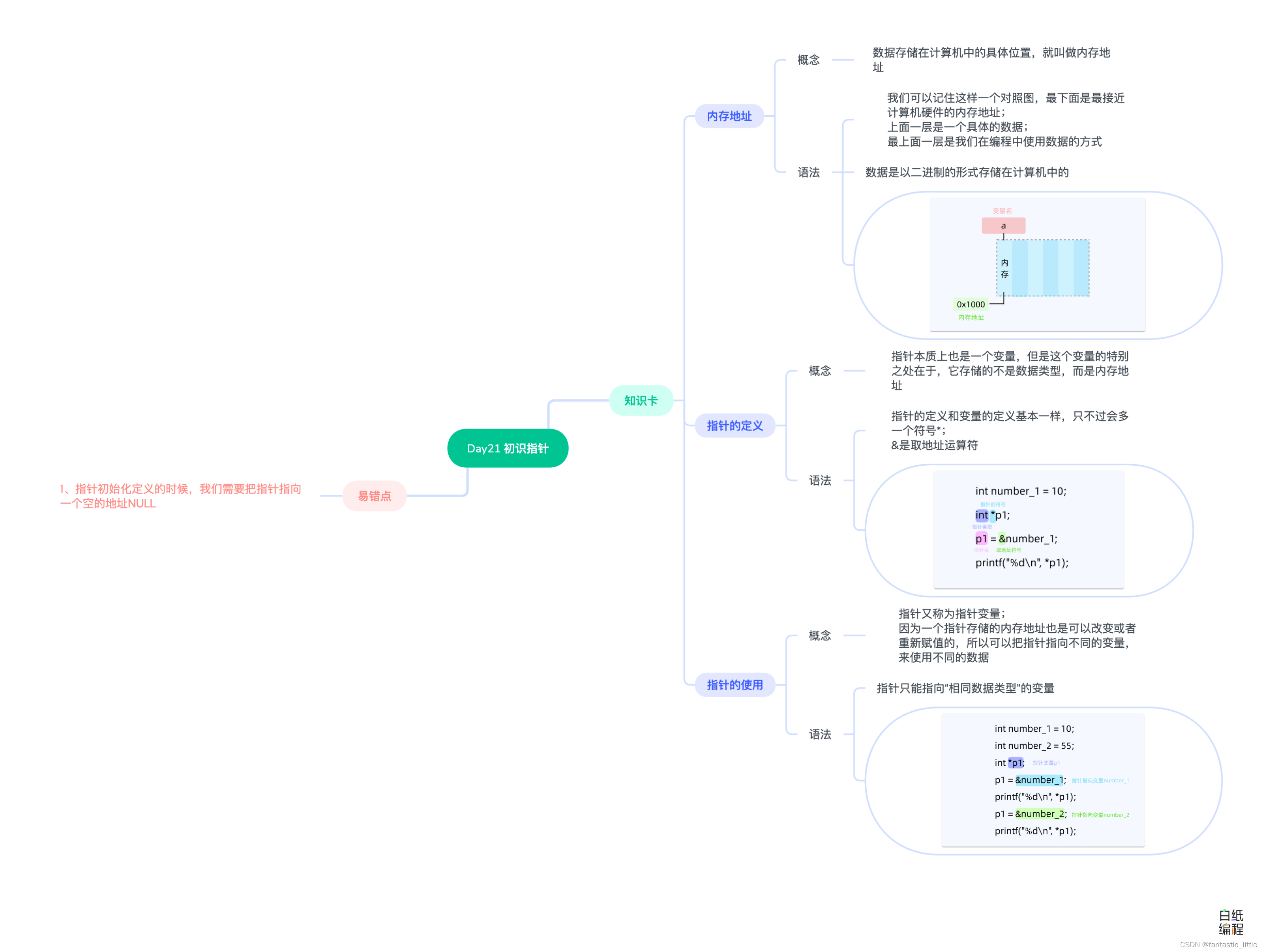
C语言入门Day_22 初识指针
目录 前言: 1.内存地址 2.指针的定义 3.指针的使用 4.易错点 5.思维导图 前言: 之前我们学过变量可以用来存储数据,就像一个盒子里面可以放不同的球一样。 这是一个方便大家理解专业概念的比喻。 在计算机世界里面,数据实…...
【面试必刷TOP101】删除链表的倒数第n个节点 两个链表的第一个公共结点
目录 题目:删除链表的倒数第n个节点_牛客题霸_牛客网 (nowcoder.com) 题目的接口: 解题思路: 代码: 过啦!!! 题目:两个链表的第一个公共结点_牛客题霸_牛客网 (nowcoder.com) …...
手刻 Deep Learning -第壹章 -PyTorch教学-激励函数与感知机入门(上)
一、前言 本文接续前篇教学 Pytorch 与线性回归 ,本文着重在 Activation Function ( 中文称 激励函数 ),我们会介绍激励函数 (也有人称 激活函数? 激发函数? ) 为什么会有用…...
物理内存分配
目录 内核物理内存分配接口 内存分配行为(物理上) 内存分配的行为操作 内存 三个水位线 水线计算 水位线影响内存分配行为 内存分配核心__alloc_pages 释放页 1、内核物理内存分配接口 struct page *alloc_pages(gfp_t gfp, unsigned int ord…...
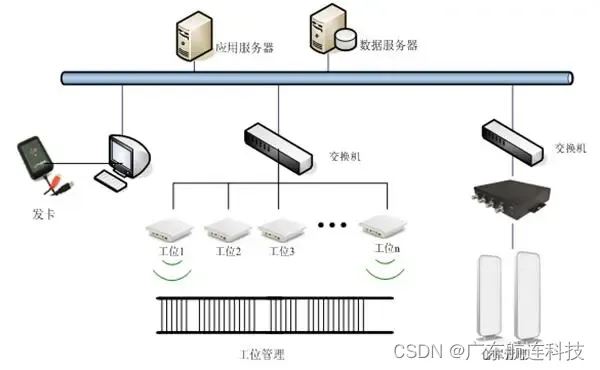
RFID产线自动化升级改造管理方案
应用背景 在现代制造业中,产线管理是实现高效生产和优质产品的关键环节,产线管理涉及到生产过程的监控、物料管理、工艺控制、质量追溯等多个方面,有效的产线管理可以提高生产效率、降低成本、改善产品质量,并满足市场需求的变化…...

全量数据采集:不同网站的方法与挑战
简介 在当今数字化时代中,有数据就能方便我们做出很多决策。数据的获取与分析已经成为学术研究、商业分析、战略决策以及个人好奇心的关键驱动力。本文将分享不同网站的全量数据采集方法,以及在这一过程中可能会遇到的挑战。 部分全量采集方法 1. 撞店…...

Redis——渐进式遍历和数据库管理命令
介绍 如果使用keys * 这样的操作,将Redis中所有的key都获取到,由于Redis是单线程工作,这个操作本身又要消耗很多时间,那么就会导致Redis服务器阻塞,后续的操作无法正常执行 而渐进式遍历,通过多次执行遍历…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
