Leetcode每日一题:打家劫舍系列Ⅰ、Ⅱ、Ⅲ、Ⅳ(2023.9.16~2023.9.19 C++)
由于之前写过打家劫舍系列,这里直接弄个合集,后面应该还有个iv。
目录
198. 打家劫舍
213. 打家劫舍 II
337. 打家劫舍 III
2560. 打家劫舍 IV
198. 打家劫舍
题目描述:
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1] 输出:12 解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
1 <= nums.length <= 1000 <= nums[i] <= 400
实现代码与解析:
方法一:
class Solution {
public:int rob(vector<int>& nums) {vector<vector<int>> f(nums.size(), vector<int>(2, 0));// f[i][0] 第i个房间不偷的最大金额,f[i][1] 第i个房间偷的最大金额f[0][0] = 0;f[0][1] = nums[0];for (int i = 1; i < nums.size(); i++){f[i][0] = max (f[i - 1][0], f[i - 1][1]);f[i][1] = f[i - 1][0] + nums[i];}return max(f[nums.size()-1][0], f[nums.size()-1][1]);}
};方法二:
class Solution {
public:int rob(vector<int>& nums) {if (nums.size() == 1) {return nums[0];}vector<int> dp = vector<int>(nums.size(), 0);dp[0] = nums[0];dp[1] = max(nums[0], nums[1]);for (int i = 2; i < nums.size(); i++) {dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);}return dp[nums.size() - 1];}
};原理思路:
两种方法,其实就是dp数组定义的含义不同,都是可以解决此题的。
方法一的dp含义:
f[i][0]表示第i个房间不偷的最大金额,最大金额等于前一个房间不偷的最大金额(f[i-1][0])或者前一个房间偷的最大金额(f[i-1][1])中的较大值。f[i][1]表示第i个房间偷的最大金额,只能选择偷第i个房间,那么最大金额等于前一个房间不偷的最大金额(f[i-1][0])加上第i个房间的财物数量(nums[i])。
方法二的dp含义:
dp[i] 表示抢劫前i个房屋所能获得的最大金额。可以选择抢劫第i个房屋,那么最大金额等于前两个房屋的最大金额(dp[i-2])加上第i个房屋的财物数量(nums[i])与不抢劫第i个房屋的最大金额(dp[i-1])中的较大值。
213. 打家劫舍 II
题目描述:
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2] 输出:3 解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入:nums = [1,2,3,1] 输出:4 解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 3:
输入:nums = [1,2,3] 输出:3
提示:
1 <= nums.length <= 1000 <= nums[i] <= 1000
实现代码与解析:
dp
class Solution {
public:int robRange(vector<int>& nums,int start,int end){if(start == end) return nums[start];// 只有一种元素vector<int> dp(nums.size());dp[start] = nums[start]; // 初始化dp[start + 1] = max(nums[start], nums[start + 1]);for(int i = start + 2; i <= end; i++){dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]);}return dp[end];}int rob(vector<int>& nums) {if(nums.size() == 0) return 0;if(nums.size() == 1) return nums[0];int result1 = robRange(nums, 0, nums.size() - 2); // 不选取最后有一个房间的最大价值int result2 = robRange(nums, 1, nums.size() - 1); // 不选取第一个房间的最大价值int result = max(result1, result2);return result;}
};原理思路:
和上一题完全相似,这里我们不考虑第一个房间或不考虑最后一个房间分别dp一下,取一个max即可。
337. 打家劫舍 III
题目描述:
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
示例 1:
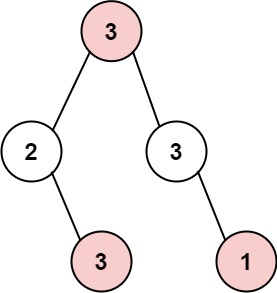
输入: root = [3,2,3,null,3,null,1] 输出: 7 解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
示例 2:
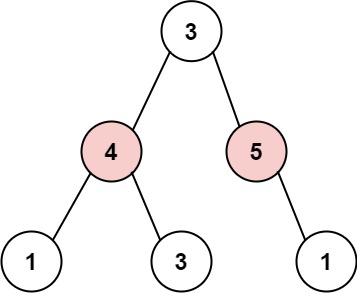
输入: root = [3,4,5,1,3,null,1] 输出: 9 解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9
提示:
- 树的节点数在
[1, 104]范围内 0 <= Node.val <= 104
实现代码与解析:
树形dp
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> dp(TreeNode* cur){if (cur == NULL) return{0, 0};// 0 不偷,1偷vector<int> left = dp(cur->left);vector<int> right = dp(cur->right);vector<int> res(2, 0);res[0] = max({left[1] + right[1], left[0] + right[0], left[0] + right[1], left[1] + right[0]}); // 不偷此房间的最大金额,注意误区,子树房间不一定偷了才是最大。 res[1] = left[0] + right[0] + cur->val;return res;}int rob(TreeNode* root) {vector<int> res = dp(root);return max(res[0], res[1]);}
};原理思路:
-
在
dp函数中,首先检查当前节点是否为NULL,如果是,则返回一个包含两个零的向量{0, 0},表示没有金额可偷。 -
接下来,递归调用
dp函数计算左子树和右子树的最大金额,分别存储在left和right向量中。 -
然后,定义一个名为
res的向量,用于存储当前节点可以偷取的最大金额,其中res[0]表示不偷当前节点,res[1]表示偷当前节点。 -
计算
res[0]的值,考虑了四种情况:- 不偷当前节点,同时也不偷左子树和右子树:
left[0] + right[0] - 不偷当前节点,但偷左子树:
left[1] + right[0] - 不偷当前节点,但偷右子树:
left[0] + right[1] - 偷当前节点,同时不偷左子树和右子树:
left[0] + right[0] + cur->val
取这四种情况中的最大值作为
res[0]的值,表示不偷当前节点的最大金额。 - 不偷当前节点,同时也不偷左子树和右子树:
-
计算
res[1]的值,即偷当前节点,同时不偷左子树和右子树,即left[0] + right[0] + cur->val。 -
最后,函数返回
res向量,其中res[0]和res[1]分别表示不偷和偷当前节点的最大金额。 -
在
rob函数中,调用dp函数来计算根节点root的最大金额,并返回其中的较大值,即max(res[0], res[1]),这是整个问题的解。
使用动态规划的思想,通过递归遍历二叉树的节点来计算最大金额。它在每个节点上都考虑了两种情况:偷取当前节点和不偷取当前节点,然后根据这两种情况的结果计算最大金额。最后,返回根节点的最大金额,即问题的解。
2560. 打家劫舍 IV
题目描述:
沿街有一排连续的房屋。每间房屋内都藏有一定的现金。现在有一位小偷计划从这些房屋中窃取现金。
由于相邻的房屋装有相互连通的防盗系统,所以小偷 不会窃取相邻的房屋 。
小偷的 窃取能力 定义为他在窃取过程中能从单间房屋中窃取的 最大金额 。
给你一个整数数组 nums 表示每间房屋存放的现金金额。形式上,从左起第 i 间房屋中放有 nums[i] 美元。
另给你一个整数 k ,表示窃贼将会窃取的 最少 房屋数。小偷总能窃取至少 k 间房屋。
返回小偷的 最小 窃取能力。
示例 1:
输入:nums = [2,3,5,9], k = 2 输出:5 解释: 小偷窃取至少 2 间房屋,共有 3 种方式: - 窃取下标 0 和 2 处的房屋,窃取能力为 max(nums[0], nums[2]) = 5 。 - 窃取下标 0 和 3 处的房屋,窃取能力为 max(nums[0], nums[3]) = 9 。 - 窃取下标 1 和 3 处的房屋,窃取能力为 max(nums[1], nums[3]) = 9 。 因此,返回 min(5, 9, 9) = 5 。
示例 2:
输入:nums = [2,7,9,3,1], k = 2 输出:2 解释:共有 7 种窃取方式。窃取能力最小的情况所对应的方式是窃取下标 0 和 4 处的房屋。返回 max(nums[0], nums[4]) = 2 。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 1091 <= k <= (nums.length + 1)/2
实现代码与解析:
二分
class Solution {
public:bool check(vector<int>& nums, int mid, int k) {int flag = 1; // 判断能否选取int count = 0; // 当前选取个数for (auto t: nums){if (t <= mid && flag){count++;flag = 0;}else {flag = 1;}}if (count < k) return false;else return true;}int minCapability(vector<int>& nums, int k) {int l = *min_element(nums.begin(), nums.end()); // 最小值int r = *max_element(nums.begin(), nums.end()); // 最大值while(l < r){int mid = (l + r) >> 1;if (check(nums, mid, k)) r = mid;else l = mid + 1;}return l;}
}原理思路:
解析题目,其实是求在选取大于k个不相邻房间的情况中,找出每种选法的最大值中的最小值。
check中,小于等于mid且此位置可以选取才能偷,此种选取最后个数大于等于k返回true,反之返回false。
相关文章:

Leetcode每日一题:打家劫舍系列Ⅰ、Ⅱ、Ⅲ、Ⅳ(2023.9.16~2023.9.19 C++)
由于之前写过打家劫舍系列,这里直接弄个合集,后面应该还有个iv。 目录 198. 打家劫舍 213. 打家劫舍 II 337. 打家劫舍 III 2560. 打家劫舍 IV 198. 打家劫舍 题目描述: 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都…...

容易对一个异性产生依赖感怎么办?
歌词:爱总让人伤心,但你要学会去明白~ 👂 Photograph - Ed Sheeran - 单曲 - 网易云音乐 目录 🌼前言 😟一、对另一个人的依赖感,本质是什么? 😊二、如何减少对伴侣的依赖感&am…...

Windows10/11无线网卡WIFI驱动详细下载安装教程
官网下载WIFI驱动 《intel官网》 找到下载Windows 10 and Windows 11* WiFi package drivers 查看详细信息 下载对应操作系统的WIFI驱动 安装驱动,然后重启电脑即可。...

面向面试知识--Lottery项目
面向面试知识–Lottery项目 1.设计模式 为什么需要设计模式? (设计模式是什么?优点有哪些?) 设计模式是一套经过验证的有效的软件开发指导思想/解决方案;提高代码的可重用性和可维护性;提高团…...
SpringBoot接口中如何直接返回图片数据
SpringBoot接口中如何直接返回图片数据 目录 接口直接返回图片数据 起因 类似这种 根据个人经验 优雅的实现图片返回 接口直接返回图片数据 起因 最近在做涉及到分享推广的业务,需要由业务员分享二维码进入推广页面,由于是新项目,前期…...

c语言进阶部分详解(指针进阶1)
大家好!指针的初阶内容我已经写好,可移步至我的文章:c语言进阶部分详解(指针初阶)_总之就是非常唔姆的博客-CSDN博客 基本内容我便不再赘述,直接带大家进入进阶内容: 目录 一.字符指针 1.讲解…...
计算机竞赛 大数据商城人流数据分析与可视化 - python 大数据分析
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于大数据的基站数据分析与可视化 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🥇学长这里给一个题目综合评分(每项满分5分) 难度…...
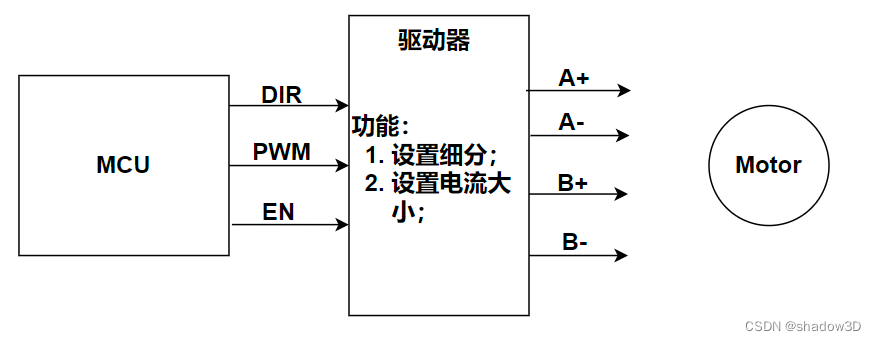
各种电机驱动原理
步进电机 步进电机参考资料 野火官方文档 步进电机驱动原理 上面参考文档中有的内容就不写了,写一下我自己的总结吧。 说明: 电机驱动器输入信号有电机转动方向信号DIR,电机转速信号PWM,电机使能信号EN;电机驱动器…...

人脸图像数据增强
为什么要做数据增强 在计算机视觉相关任务中,数据增强(Data Augmentation)是一种常用的技术,用于扩展训练数据集的多样性。它包括对原始图像进行一系列随机或有规律的变换,以生成新的训练样本。数据增强的主要目的是增…...

Android 查看按键信息的常用命令详解
Android 查看按键信息的常用命令详解 文章目录 Android 查看按键信息的常用命令详解一、主要命令:二、命令详解1、getevent2、getevent -l3、dumsys input4、cat XXX.kl4、cat /dev/input/eventX5、getevent 其他命令6、input keyevent XX 三、简单示例修改四、总结…...

【Java 基础篇】Properties 结合集合类的使用详解
Java 中的 Properties 类是一个常见的用于管理配置信息的工具,它可以被看作是一种键值对的集合。虽然 Properties 通常用于处理配置文件,但它实际上也可以作为通用的 Map 集合来使用。在本文中,我们将详细探讨如何使用 Properties 作为 Map 集…...

数字孪生体标准编程
数字孪生体标准 括ISO TC184/SC4正在制定数字孪生制造标准ISO 23247、ISO/IEC JTC1/AG11正在推动数字孪生体标准、IEEE P2806正在做有关“数字表达”的标准。赢家通吃的标准战 卡尔夏皮罗和哈尔范里安撰写了《信息规则:网络经济战略指南》(Information R…...

力扣 -- 394. 字符串解码
解题方法: 参考代码: class Solution{ public:string decodeString(string s){stack<string> sst;stack<int> dst;//防止字符串栈为空的时候再追加字符串到栈顶元素sst.push("");int n s.size();int i 0;while(i<n)//最好不…...

面试官:什么是虚拟DOM?如何实现一个虚拟DOM?说说你的思路
🎬 岸边的风:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 一、什么是虚拟DOM 二、为什么需要虚拟DOM 三、如何实现虚拟DOM 小结 一、什么是虚拟DOM 虚拟 DOM (…...

Ubuntu安装中文拼音输入法
ubuntu安装中文拼音输入法 ubuntu版本为23.04 1、安装中文语言包 首先安装中文输入法必须要让系统支持中文语言,可以在 Language Support 中安装中文语言包。 添加或删除语音选项,添加中文简体,然后会有Applying changes的对话框&#x…...

高端知识竞赛中用到的软件和硬件有哪些
现在单位搞知识竞赛,已不满足于用PPT放题,找几个简单的抢答器、计分牌弄一下了,而是对现场效果和科技感要求更高了。大屏要分主屏侧屏,显示内容要求丰富炫酷;选手和评委也要用到平板等设备;计分要大气些&am…...

Vue 3.3 发布
本文为翻译 原文地址:宣布推出 Vue 3.3 |The Vue Point (vuejs.org) 今天我们很高兴地宣布 Vue 3.3 “Rurouni Kenshin” 的发布! 此版本侧重于开发人员体验改进 - 特别是 TypeScript 的 SFC <script setup> 使用。结合 Vue Language Tools&…...

算法|图论 3
LeetCode 130- 被围绕的区域 题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目描述:给你一个 m x n 的矩阵 board ,由若干字符 X 和 O ,找到所有被 X 围绕的区域,并将这些区域…...
【数据结构】二叉树的层序遍历(四)
目录 一,层序遍历概念 二,层序遍历的实现 1,层序遍历的实现思路 2,创建队列 Queue.h Queue.c 3,创建二叉树 BTree.h BTree.c 4,层序遍历的实现 一,层序遍历概念 层序遍历:除了先序…...
macOS文件差异比较最佳工具:Beyond Compare 4
Beyond Compare for mac是一款Scooter Software研发的文件同步对比工具。你可以选择针对多字节的文本、文件夹、源代码,甚至是支持比对adobe文件、pdf文件或是整个驱动器,检查其文件大小、名称、日期等信息。你也可以选择使用Beyond Compare合并两个不同…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
