服务网格的面临挑战:探讨服务网格实施中可能遇到的问题和解决方案
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁
🦄 博客首页——猫头虎的博客🎐
🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺
🌊 《IDEA开发秘籍专栏》学会IDEA常用操作,工作效率翻倍~💐
🌊 《100天精通Golang(基础入门篇)》学会Golang语言,畅玩云原生,走遍大小厂~💐
🪁🍁 希望本文能够给您带来一定的帮助🌸文章粗浅,敬请批评指正!🍁🐥
文章目录
- 《服务网格的面临挑战:探讨服务网格实施中可能遇到的问题和解决方案》
- 🐯摘要
- 🎈引言
- 📜正文
- 1. 服务网格的挑战
- 1.1 复杂性
- 1.2 性能开销
- 1.3 兼容性问题
- 2. 解决方案
- 2.1 简化部署
- 2.2 优化性能
- 2.3 增强兼容性
- 3. 案例分析
- 3.1 挑战
- 3.2 解决方案
- 4. 未来展望
- 4.1 更高的性能
- 4.2 更强大的功能
- 🌈总结
- 📚参考资料
- 原创声明
《服务网格的面临挑战:探讨服务网格实施中可能遇到的问题和解决方案》
🐯摘要
🎉大家好!猫头虎博主今天带来了一篇热门话题——服务网格!虽然服务网格为云原生应用提供了强大的网络能力,但在实施过程中,它也带来了一系列挑战。在这篇文章中,我们将深入探讨这些挑战,并提供相应的解决方案。对于关心微服务、服务网格和云原生技术 热门词汇的朋友,这篇文章绝对不能错过!🚀
🎈引言
服务网格作为微服务架构的一个核心组件,为我们提供了强大的流量管理、安全和监控功能。但像所有新技术一样,实施服务网格也有其困难和挑战。
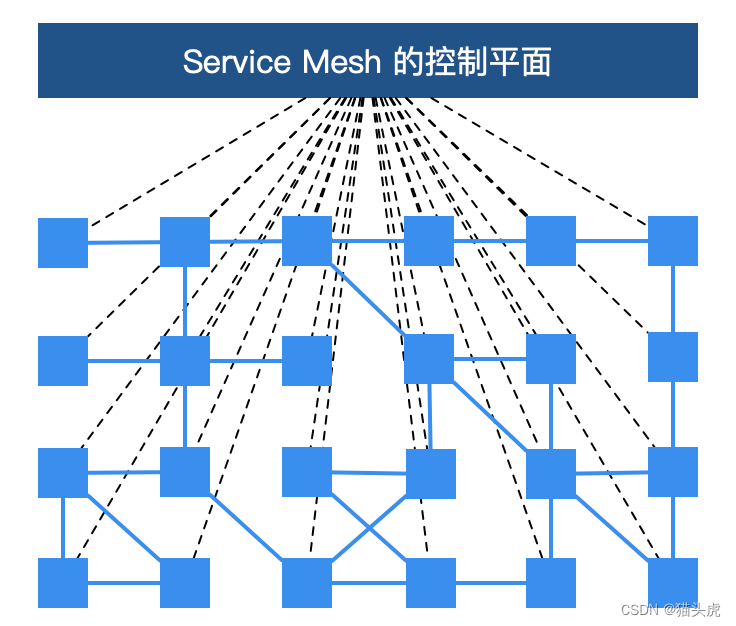
📜正文
1. 服务网格的挑战
服务网格虽然强大,但在实施过程中,开发者和运维人员可能会遇到以下挑战。
1.1 复杂性
服务网格引入了一个新的层,增加了系统的复杂性。
1.2 性能开销
为每个服务注入代理会带来额外的性能开销。
1.3 兼容性问题
与现有的网络和安全解决方案可能存在兼容性问题。
2. 解决方案
面对这些挑战,我们可以采取以下策略。
2.1 简化部署
使用自动化工具,如Helm或Kustomize,简化部署过程。
helm install my-mesh stable/service-mesh
2.2 优化性能
- 选择轻量级的代理,如Envoy或Linkerd。
- 根据需要调整代理的资源配额。
resources:requests:cpu: "100m"memory: "128Mi"
2.3 增强兼容性
- 使用开放标准,如SPIFFE,确保安全的服务间通信。
- 选择支持多种协议和平台的服务网格。
3. 案例分析
让我们通过一个真实的案例来了解服务网格的挑战和解决方案。
3.1 挑战
一家大型电商公司在引入服务网格后,发现其订单服务的响应时间增加了20%。
3.2 解决方案
- 优化代理配置,减少不必要的日志记录和指标收集。
- 调整服务的资源配额,确保代理有足够的CPU和内存。
4. 未来展望
随着服务网格技术的发展,我们期待更多的优化和创新。
4.1 更高的性能
随着硬件和软件的进步,服务网格的性能会进一步提高。
4.2 更强大的功能
未来的服务网格将提供更丰富的流量管理、安全和监控功能。
🌈总结
服务网格为微服务架构带来了巨大的价值,但同时也带来了一系列挑战。通过深入了解这些挑战并采取相应的解决方案,我们可以确保服务网格的成功实施,并充分发挥其价值。
📚参考资料
- 《服务网格:原理与实践》
- 《微服务的网络挑战》
- 《云原生应用的流量管理》
感谢大家的阅读,我是猫头虎博主,期待下次与你相见!🐯👋🎉

原创声明
======= ·
- 原创作者: 猫头虎
作者wx: [ libin9iOak ]
| 学习 | 复习 |
|---|---|
| ✔ |
本文为原创文章,版权归作者所有。未经许可,禁止转载、复制或引用。
作者保证信息真实可靠,但不对准确性和完整性承担责任。
未经许可,禁止商业用途。
如有疑问或建议,请联系作者。
感谢您的支持与尊重。
点击
下方名片,加入IT技术核心学习团队。一起探索科技的未来,共同成长。
相关文章:

服务网格的面临挑战:探讨服务网格实施中可能遇到的问题和解决方案
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

leetcode61 旋转链表
题目 给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。 示例 输入:head [1,2,3,4,5], k 2 输出:[4,5,1,2,3] 解析 这道题属实不好想:需要计算出链表的长度,然后在k > n的…...
【学习笔记】各类基于决策单调性的dp优化
文章目录 对于决策单调性的一般解释关于决策单调性的证明四边形不等式一维dp区间dp一种二维dp一些满足四边形不等式的函数类 与图形相结合 决策单调性的常见优化手段二分队列二分栈分治类莫队做法 SMAWKWQS二分WQS多解情况满足四边形不等式的序列划分问题的答案凸性以及WQS二分…...
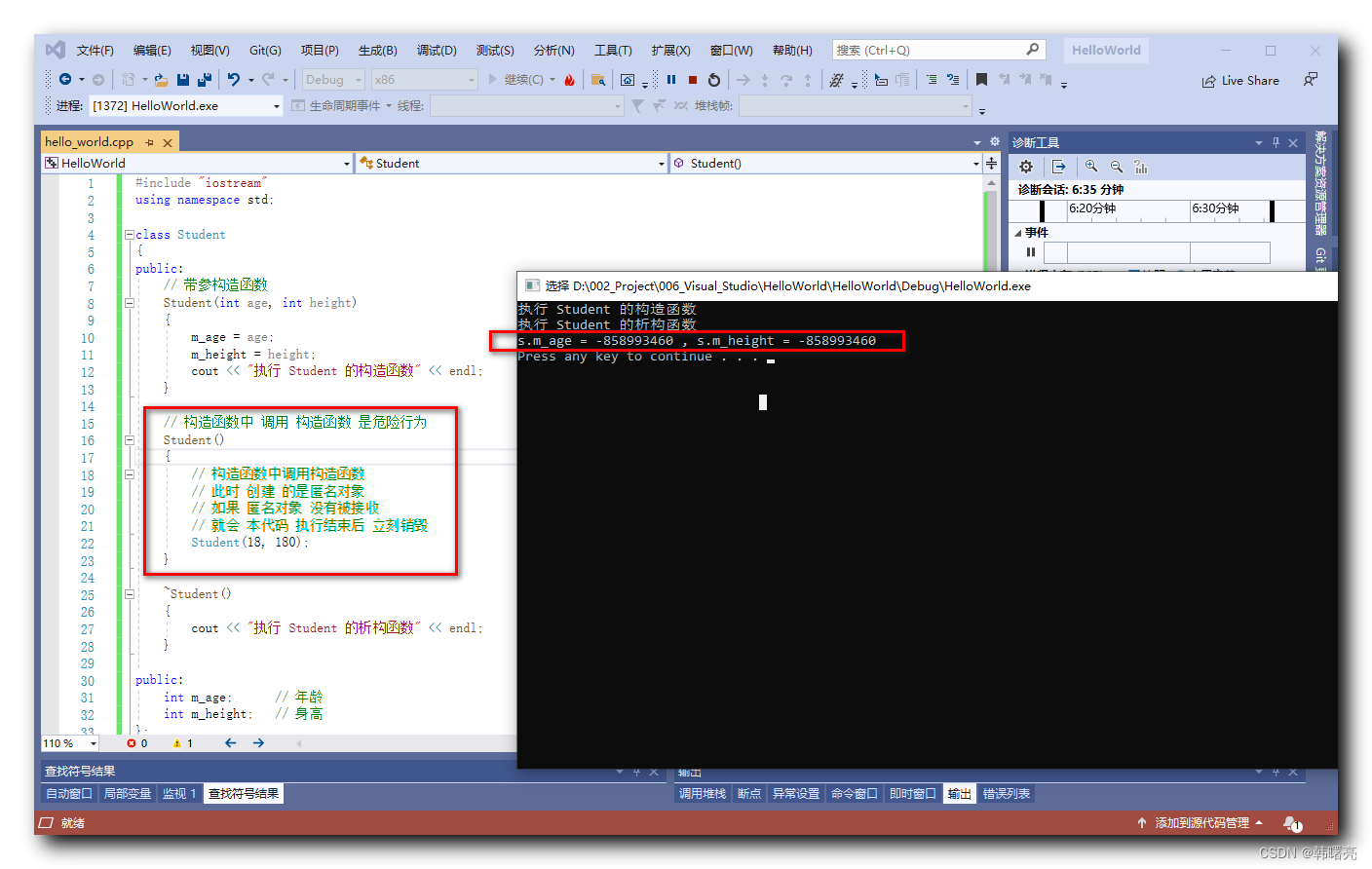
【C++】构造函数初始化列表 ⑤ ( 匿名对象 生命周期 | 构造函数 中 不能调用 构造函数 )
文章目录 一、匿名对象 生命周期1、匿名对象 生命周期 说明2、代码示例 - 匿名对象 生命周期 二、构造函数 中调用 构造函数1、构造函数 中 不能调用 构造函数2、代码示例 - 构造函数中调用构造函数 构造函数初始化列表 总结 : 初始化列表 可以 为 类的 成员变量 提供初始值 ;…...

Knife4j系列--使用方法
原文网址:Knife4j系列--使用/教程/实例/配置_IT利刃出鞘的博客-CSDN博客...

pmp项目管理考试是什么?适合哪些人学?
PMP,简单点说,就是美国PMI为考察项目管理人士的专业能力而设立的考试。 该流程以知识和任务驱动型指南评估从业者的能力,同时确定项目经理能力行业标准,包括各项知识、任务和技能的特点、重要性与运用频率。(考纲原文…...
CSDN博客可以添加联系方式了
csdn博客一直不允许留一些联系方式,结果是官方有联系方式路径 在首页,往下拉,左侧就有 点击这个即可添加好友了~ 美滋滋,一起交流, 学习技术 ~...
小程序隐私弹窗的实现
小程序的开发者对于微信官方来说是有爱有恨,三天二头整事是鹅厂的一贯风格。 隐私弹窗的几个要点 回归正题,小程序隐私弹窗的几个要点: 1、何时弹出用户隐私协议的弹窗? 2、是每次进小程序都弹出来吗? 这两个想明…...
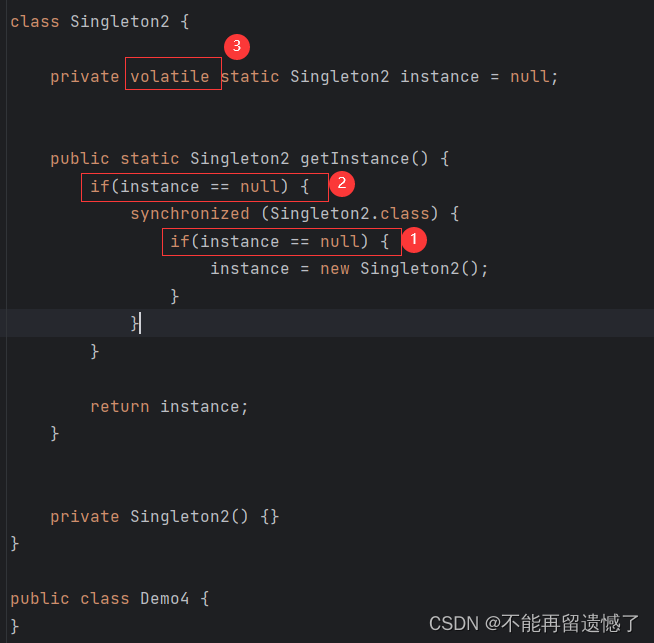
【JavaEE】多线程案例-单例模式
文章目录 1. 前言2. 什么是单例模式3. 如何实现单例模式3.1 饿汉模式3.2 懒汉模式4. 解决单例模式中遇到的线程安全问题4.1 加锁4.2 加上一个判断解决频繁加锁问题4.2 解决因指令重排序造成的线程不安全问题 1. 前言 单例模式是我们面试中最常考到的设计模式。什么是设计模式呢…...

社区分享|MeterSphere变身“啄木鸟”,助力云帐房落地接口自动化测试
云帐房网络科技有限公司(以下简称为“云帐房”)成立于2015年3月,以“成为最值得信赖的税务智能公司”为愿景,运用人工智能、大数据等互联网技术,结合深厚的财税行业服务经验,为代账公司和中大型企业提供智能…...
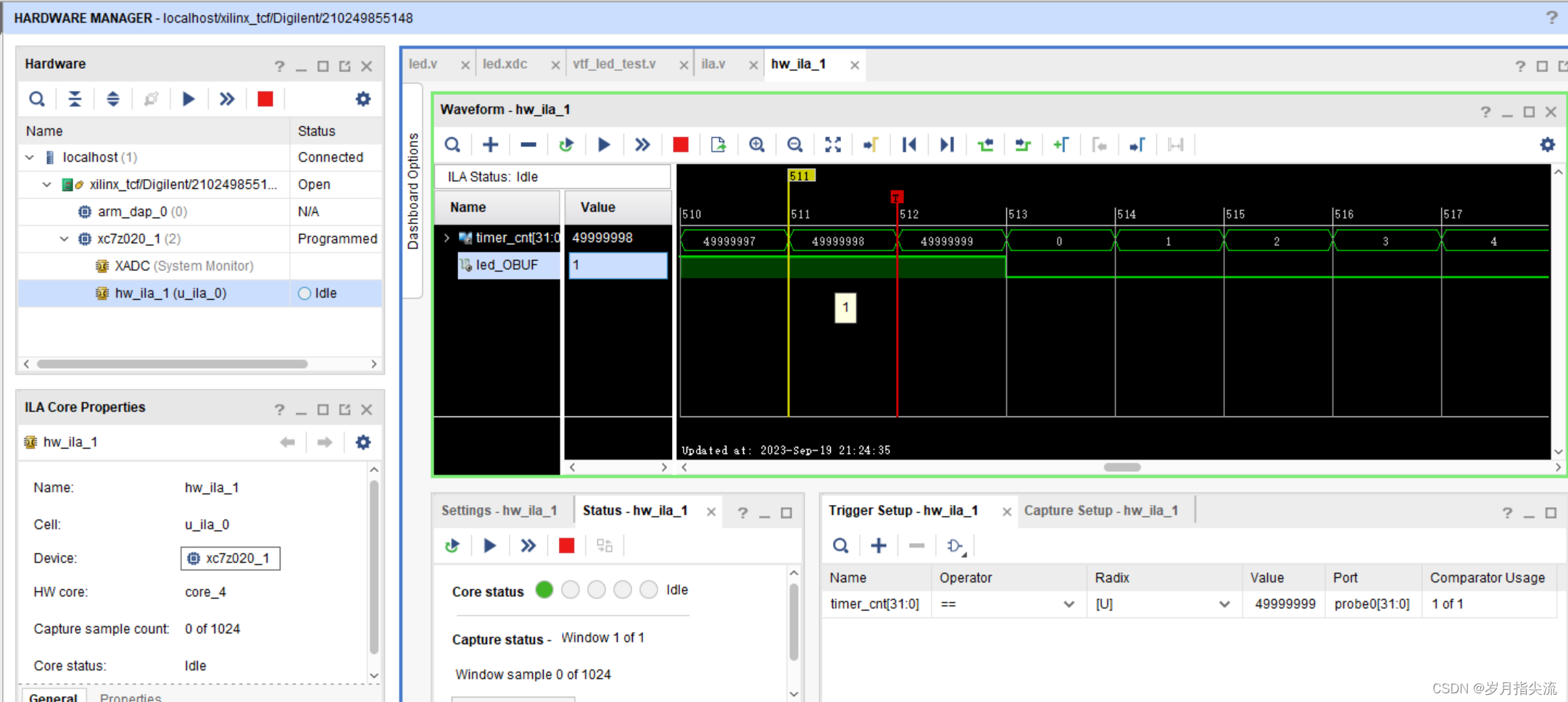
fpga内嵌逻辑分析仪使用方法
文章目录 前言一、方法1 — 使用 IP 核创建 ILA 调试环境1、创建 ILA ip 核2、进行例化3、生成比特流文件4、下载程序5、进行在线调试 二、方法2 — 使用 Debug 标记创建 ILA1、Debug 标记相关信号2、综合操作3、设置 Set Up Debug4、生成比特文件5、下载程序6、进行在线调试 前…...

第14章 结构和其他数据形式
本章介绍以下内容: 关键字:struct、union、typedef 运算符:.、-> 什么是C结构,如何创建结构模板和结构变量 如何访问结构的成员,如何编写处理结构的函数 联合和指向函数的指针 设计程序时,最重要的步骤之…...
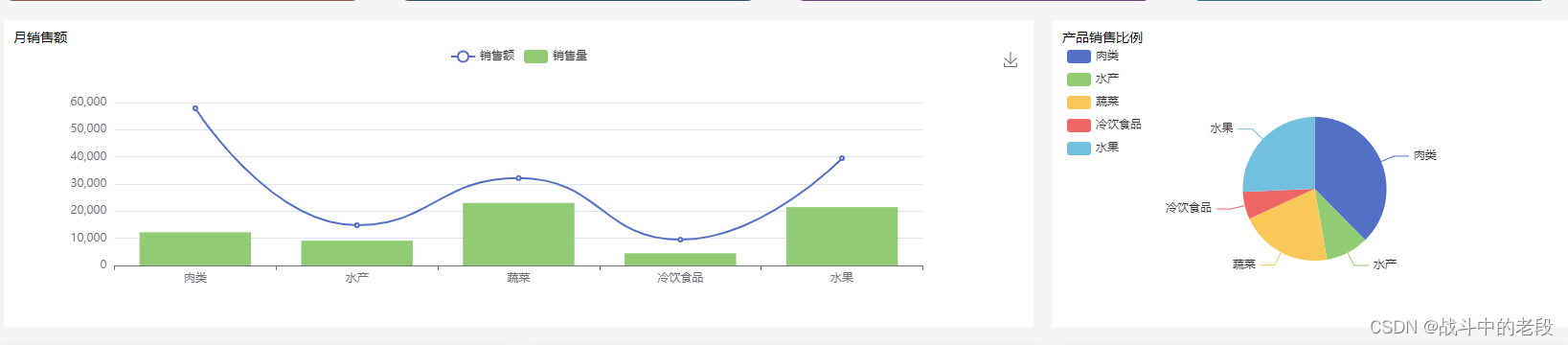
vue 把echarts封装成一个方法 并且从后端读取数据 +转换数据格式 =动态echarts 联动echarts表
1.把echarts 在 methods 封装成一个方法mounted 在中调用 折线图 和柱状图 mounted调用下边两个方法 mounted(){//最早获取DOM元素的生命周期函数 挂载完毕console.log(mounted-id , document.getElementById(charts))this.line()this.pie()},methods里边的方法 line() {// …...

Python基础08 面向对象的基本概念
Python使用类(class)和对象(object),进行面向对象(object-oriented programming,简称OOP)的编程。 面向对象的最主要目的是提高程序的重复使用性。我们这么早切入面向对象编程的原因是,Python的整个概念是基于对象的。…...

APP自动化之Poco框架
今天给大家介绍一款自动化测试框架Poco,其脚本写法非常简洁、高效,其元素定位器效率更快,其本质基于python的第三方库,调试起来也会非常方便,能够很好的提升自动化测试效率,节省时间。 (一)背景…...

c++拷贝构造【显式调用】和运算符=重载构造【隐式调用】解析
深拷贝 vs. 浅拷贝 深拷贝:开辟新内存,独立对象,堆区浅拷贝:共享内存,引用对象,栈区 深拷贝:深拷贝是一种拷贝方式,它会在堆区重新分配内存并复制对象的内容。 这意味着原对象和新…...

无涯教程-JavaScript - LCM函数
描述 LCM函数返回整数的最小公倍数。最小公倍数是最小的正整数,它是所有整数参数number1,number2等的倍数。使用LCM添加具有不同分母的分数。 语法 LCM (number1, [number2] ...)争论 Argument描述Required/OptionalNumber1, number2... 您想要最小公倍数的1到255个值。 如…...
Java多线程篇(3)——线程池
文章目录 线程池ThreadPoolExecutor源码分析1、如何提交任务2、如何执行任务3、如何停止过期的非核心线程4、如何使用拒绝策略 ScheduledThreadPoolExecutor源码分析 线程池 快速过一遍基础知识 7大参数 corePoolSize : 核心线程数 maximumPoolSize: 最…...

那些年我们遇到过的关于excel的操作
本文为直接从百度上搜索的关于excel的函数使用,方便以后用,希望会持续补充 excel中筛选出两列重复的数据【场景:A、B两列数据个数不同且无序,想找出A列中的数据在B列中不存在的,通过比较后单元格为空的代表该行不存在的…...

Angular变更检测机制
前段时间遇到这样一个 bug,通过一个 click 事件跳转到一个新页面,新页面迟迟不加载; 经过多次测试发现,将鼠标移入某个 tab ,页面就加载出来了。 举个例子,页面内容无法加载,但是将鼠标移入下图…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
