矩阵 m * M = c
文章目录
- 题1
- 题2
题1
(2023江苏领航杯-prng)
题目来源:https://dexterjie.github.io/2023/09/12/%E8%B5%9B%E9%A2%98%E5%A4%8D%E7%8E%B0/2023%E9%A2%86%E8%88%AA%E6%9D%AF/
题目描述:
(没有原数据,自己生成的数据)
from Crypto.Util.number import *
from secret import flag
import random def base(n, l): bb = [] while n > 0: n, r = divmod(n, l) bb.append(r) return ''.join(str(d) for d in bb[::-1]) def prng(secret): seed = base(secret, 5) seed = [int(i) for i in list(seed)] length = len(seed) R = [[ random.randint(0,4) for _ in range(length)] for _ in range(length*2)] S = [] for r in R: s = 0 for index in range(length): s += (r[index] * seed[index]) % 5 s %= 5 S.append(s) return R, S m = bytes_to_long(flag)
R, S = prng(m) with open('output.txt', 'w') as f: f.write(f'R = {R}\nS = {S}')
题目分析:
( R 1 , 1 R 1 , 2 ⋯ R 1 , n R 2 , 1 R 2 , 2 ⋯ R 2 , n ⋮ ⋮ ⋱ ⋮ R 2 n , 1 R 2 n , 2 ⋯ R 2 n , n ) ∗ ( s e e d 1 s e e d 2 ⋮ s e e d n ) = ( S 1 S 2 ⋯ S 2 n ) \begin{pmatrix} R_{1,1}&R_{1,2}&\cdots&R_{1,n}\\ R_{2,1}&R_{2,2}&\cdots&R_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ R_{2n,1}&R_{2n,2}&\cdots&R_{2n,n} \end{pmatrix}* \begin{pmatrix} seed_1\\ seed_2\\ \vdots\\ seed_n \end{pmatrix} = \begin{pmatrix} S_1&S_2&\cdots&S_{2n} \end{pmatrix} R1,1R2,1⋮R2n,1R1,2R2,2⋮R2n,2⋯⋯⋱⋯R1,nR2,n⋮R2n,n ∗ seed1seed2⋮seedn =(S1S2⋯S2n)
5进制,R * seed = S,已知R,S求seed
from Crypto.Util.number import *
from gmpy2 import *
with open('output1.txt') as f:exec(f.read())
p = 5
R = matrix(GF(5),R).transpose()
S = matrix(GF(5),S)
m = R.solve_left(S).list()
print(long_to_bytes(int(''.join(str(i) for i in m),5)))# CnHongKe{a8cc755d375811f55cec82153388c}
题2
题目来源:https://blog.csdn.net/weixin_52640415/article/details/132925227?spm=1001.2014.3001.5502
题目描述:
(没有原数据,自己生成的数据)
import os
import secret
import hashlib
from Crypto.Util.number import getPrime
from Crypto.Util.Padding import padLEN = 32def xor(a, b):return bytes([a[i%len(a)] ^^ b[i%len(b)] for i in range(max(len(a), len(b)))])def challenge(m: bytes, pbits: int, level: int=0):p = getPrime(pbits)M = random_matrix(GF(p), LEN).matrix_from_rows_and_columns(range(LEN), range(LEN-level))c = vector(GF(p), m) * Mreturn {"p": p, "M": M.list(), "c": c.list()}args = {"chall1": {"m": os.urandom(LEN),"pbits": 512,"level": 0x00},"chall2": {"m": os.urandom(LEN),"pbits": 10,"level": 0x01},"chall3": {"m": os.urandom(LEN),"pbits": 256,"level": 0x10}
}out = dict()
enc = pad(secret.flag, LEN)
for i in range(3):out[f"chall{i+1}"] = challenge(**args[f"chall{i+1}"])enc = xor(enc, hashlib.sha512(args[f"chall{i+1}"]["m"]).digest())
out["enc"] = enc.hex()
with open('output.txt', 'w') as f:f.write(f"{out = }")
题目分析:
m ∗ M = c ,已知 M , c 求 m 共有三组数据,求解三组矩阵 第一组: m 1 ∗ 32 ∗ M 32 ∗ 32 = c 1 ∗ 32 第二组: m 1 ∗ 32 ∗ M 32 ∗ 31 = c 1 ∗ 31 第三组: m 1 ∗ 32 ∗ M 32 ∗ 16 = c 1 ∗ 16 m * M = c,已知M,c求m\\ 共有三组数据,求解三组矩阵\\ 第一组:m_{1*32} * M_{32 * 32} = c_{1 * 32}\\ 第二组:m_{1 * 32} * M_{32 * 31} = c_{1 * 31}\\ 第三组:m_{1 * 32} * M_{32 * 16} = c_{1 * 16}\\ m∗M=c,已知M,c求m共有三组数据,求解三组矩阵第一组:m1∗32∗M32∗32=c1∗32第二组:m1∗32∗M32∗31=c1∗31第三组:m1∗32∗M32∗16=c1∗16
第一组为方阵,用solve_left()直接解
with open('output.txt') as f:exec(f.read())
len = 32p1,M1,c1 = out['chall1']['p'],out['chall1']['M'],out['chall1']['c']
M1 = Matrix(GF(p1),len,len,M1)
c1 = vector(GF(p1),c1)
m1 = M1.solve_left(c1)
print(m1)
bytes([i for i in m1])# b'\xcd\xf4\xd6\xa5#\xa2\x04~q\xf6\x90\xb6@\xf9Z\xbd\x1fw\xfe\\w\xc3\xad\xabQZBQk\xa0L\xc5'
话说非方阵是有无数组解的,solve_left()也可解非方阵,比如题1,所以来到第二组
看大佬博客是这样解的:
p2,M2,c2 = out['chall2']['p'],out['chall2']['M'],out['chall2']['c']
M2 = Matrix(GF(p2),len,len-1,M2)
c2 = Matrix(GF(p2),1,31,c2)
m2 = M2.solve_left(c2).list()
print(m2)basis = M2.left_kernel().basis()[0]
for k in range(p2): try:m21 = m2 + k * basisprint(k, bytes(m21.list())) # 题目中m是byte类型,把超过256的过滤掉except:pass
说明一下
basis 是矩阵 M 的左核空间(left kernel space)中的一个基向量。
左核空间是指满足方程 M * v = 0 的所有向量 v 的集合。
这些向量使得将它们与矩阵 M 进行乘法运算的结果为零向量
不过我很不理解为什么出来的m2是1 * 32的(虽然最后一个元素是0),但不应该是1 * 31吗。题1也不是这样啊,题一求得的seed是1 * n的。这个疑问先留下,我们继续。
这里确实是特殊的,题目中明确了m是byte类型,范围是1~256,不过有限域的范围是p,比256大得多,故通过M2.solve_left(c2)得到的m2并不是最终解,只能说这也是一个解,不过不是我们需要的解。通过爆破将解中的元素锁定在 1 ~ 256的范围内。(通过看他写的题解,我是这样理解的)
第三部分
试了下用solve_left()解,结果可想而知,是有解,不过不是我们要的,解出的数值太太太大了,M3与方阵相差太大,造basis也没用了。
如何将解中数值的范围锁定在1 ~ 256?------ 格基规约(又学到了,记下)
佬的方法:
构造如下块矩阵 ( M 1 p 0 c 0 ) 49 ∗ 48 其中 1 是 32 ∗ 32 的单位矩阵 p = ( p p ⋱ p ) 16 ∗ 16 构造如下块矩阵\\ \begin{pmatrix} M&1\\ p&0\\ c&0 \end{pmatrix}_{49 * 48}\\ \ \\ 其中1是32 * 32的单位矩阵\\ \ \\ p = \begin{pmatrix} p&&&\\ &p&&\\ &&\ddots&\\ &&&p \end{pmatrix}_{16 * 16} 构造如下块矩阵 Mpc100 49∗48 其中1是32∗32的单位矩阵 p= pp⋱p 16∗16
规约后第二行是目标向量,第一行是0向量
p3,M3,c3 = out['chall3']['p'],out['chall3']['M'],out['chall3']['c']
M3 = matrix(ZZ,32,16,M3)
c3 = matrix(ZZ,1,16,c3)
A = block_matrix([[M3,1],[Integer(p3),0],[c3,0]])
m33 = A.LLL()
m3 = bytes(map(abs,m33[1][16:]))
print(m3)
# b'f\xcb\xf1L\xaf\xf2\xf3@a\\4\xb4[op\xa1`\x0c\x0b\x89\xa7\x1e?\x10x\x1e\xf68\xb8\xb9\x9d\xb9'
之后全部异或即可得到flag
from hashlib import *
m1 = sha512(b'\xcd\xf4\xd6\xa5#\xa2\x04~q\xf6\x90\xb6@\xf9Z\xbd\x1fw\xfe\\w\xc3\xad\xabQZBQk\xa0L\xc5').digest()
m2 = sha512(b'\x90\x1b\x87\x9c!\xe4\x92\xef\xd4\xe8\x94\x8f\x1c,\x02N\x80\x97\xb5ep\x90\x06\x8f ]\xba\x9f\xc1N\xb8Z').digest()
m3 = sha512(b'f\xcb\xf1L\xaf\xf2\xf3@a\\4\xb4[op\xa1`\x0c\x0b\x89\xa7\x1e?\x10x\x1e\xf68\xb8\xb9\x9d\xb9').digest()
enc = bytes.fromhex('496415ff125bacee09c8e721f8adf44158e398a854a48415110d0cf88fdc03767b93f91142e035e718d6ad6b7965d15a973cb9fb97923d1a37580cf60f48eabc')
print(len(m1),len(m2),len(m3))
flag = bytes([m1[i] ^ m2[i] ^ m3[i] ^ enc[i] for i in range(len(enc))])
print(flag)
浅记一下:
解疑:为什么是1 * 32 而不是1 * 31,我觉得应该是相差太小,而且,最后一位本来就是0,没有实际意义,它乘出来的结果和 1 * 31乘出来的结果本就相同,故这个1 * 32 的结果很大意义上是等同于1 * 31 的。
还有,不要用题2第三部分的解法去解题1,没用,解不出,如果对题1构造格,格中向量与想要得到的目标向量相差过小(都在GF(5)中),规约不出,得不到结果。
题2真的学到了
记点:块矩阵的构造,left_kernel().basis()的应用
还有一点,题2不要构造下面这种,也得不到结果,矩阵构造不一样结果不一样很正常,反正就是那个对按哪个来。嗯,没了。
( M 1 , 1 ⋯ M 1 , 16 1 M 2 , 1 ⋯ M 2 , 16 1 ⋮ ⋱ ⋮ ⋱ M 32 , 1 ⋯ M 32 , 16 1 p ⋯ p c 1 ⋯ c 16 ) 34 ∗ 48 \begin{pmatrix} M_{1,1}&\cdots&M_{1,16}&1&&&\\ M_{2,1}&\cdots&M_{2,16}&&1&&\\ \vdots&\ddots&\vdots&&&\ddots&\\ M_{32,1}&\cdots&M_{32,16}&&&&1\\ p&\cdots&p\\ c_1&\cdots&c_{16} \end{pmatrix}_{34*48} M1,1M2,1⋮M32,1pc1⋯⋯⋱⋯⋯⋯M1,16M2,16⋮M32,16pc1611⋱1 34∗48
相关文章:

矩阵 m * M = c
文章目录 题1题2 题1 (2023江苏领航杯-prng) 题目来源:https://dexterjie.github.io/2023/09/12/%E8%B5%9B%E9%A2%98%E5%A4%8D%E7%8E%B0/2023%E9%A2%86%E8%88%AA%E6%9D%AF/ 题目描述: (没有原数据,自己生成的数据) from Crypto.Util.number…...

Linux——IO
✅<1>主页::我的代码爱吃辣 📃<2>知识讲解:Linux——文件系统 ☂️<3>开发环境:Centos7 💬<4>前言:是不是只有C/C有文件操作呢?python,java&…...
svn(乌龟svn)和SVN-VS2022插件(visualsvn) 下载
下载地址: https://www.visualsvn.com/visualsvn/download/...
开源日报 0824 | 构建UI组件和页面的前端工作坊
Storybook 是一个用于构建 UI 组件和页面的前端工作坊,支持多种主流框架,提供丰富的插件,具有可配置性强和扩展性好的特点。 storybookjs/storybook Stars: 79.9k License: MIT Storybook 是一个用于构建 UI 组件和页面的前端工作坊&#x…...

福建三明大型工程机械3D扫描工程零件三维建模逆向抄数-CASAIM中科广电
高精度3D扫描技术已经在大型工件制造领域发挥着重要作用,可以高精度高效率实现全尺寸三维测量,本期,我们要分享的应用是大型工程机械3D扫描案例。 铣轮是深基础施工领域内工法先进、技术复杂程度高、高附加值的地连墙设备,具有成…...
使用香橙派学习 Linux的守护进程
Q:什么是守护进程 A:Linux Daemon(守护进程)是运行在后台的一种特殊进程。它独立于控制终端并且周期性地执行 某种任务或等待处理某些发生的事件。它不需要用户输入就能运行而且提供某种服务,不是对整个系统就是对某个…...

数据治理-数据仓库和商务智能
数据仓库的作用 减少数据冗余,提高信息一致性,让企业能够利用数据做出更优决策的方法,数据仓库是企业数据管理的核心。 业务驱动因素 运营支持职能、合规需求(历史数据响应)和商务智能活动(主因࿱…...

CH2--x86系统架构概览
2.1 OVERVIEW OF THE SYSTEM-LEVEL ARCHITECTURE 图中的实线箭头表示线性地址,虚线表示段选择器,虚线箭头表示物理地址 2.1.1 Global and Local Descriptor Tables 全局描述符表 (GDT) GDT是一个全局的段描述符表,它存储在系统内存中的一个固…...

Immutable.js API 简介
Immutable-js 这个库的实现是深拷贝还是浅拷贝?immutable 来源immutable.js三大特性: 持久化数据结构结构共享惰性操作 Immutable.js 的几种数据类型 immutable 使用 使用 npm 安装 immutable: 常用API介绍 MapListList.isList() 和 Map.isMa…...
)
HLSL 入门(一)
HLSL High Level Shader Language 高级着色语言,是Direct3D中用来编写Shader的语言。其语法类似于C语言。 虽然其主要作用是用来编写例如顶点着色器,像素着色器。但本质是对图形并行管线进行编程,因此也能用来编写用于计算的着色器ÿ…...

【Docker】挂载数据卷
一、Docker数据卷说明及操作 在Docker中挂载数据卷是一种将数据持久化保存的方法,以便容器之间或容器与主机之间共享数据。以下是如何在Docker中挂载数据卷的步骤: 1、创建数据卷 首先,您需要创建一个数据卷。可以使用以下命令创建一个数据卷…...

[技术干货]spring 和spring boot区别
Spring 和 Spring Boot 都是 Java 框架,用于构建企业级应用程序。Spring 是一个完整的框架,提供各种功能,包括依赖注入、事务管理、数据访问、Web 开发等。Spring Boot 是一个基于 Spring 的框架,旨在简化 Spring 应用程序的开发和…...

【hudi】数据湖客户端运维工具Hudi-Cli实战
数据湖客户端运维工具Hudi-Cli实战 help hudi:student_mysql_cdc_hudi_fl->help AVAILABLE COMMANDSArchived Commits Commandtrigger archival: trigger archivalshow archived commits: Read commits from archived files and show detailsshow archived commit stats: …...

RK3588 添加ROOT权限
一.ROOT简介 ROOT权限是Linux和Unix系统中的超级管理员用户帐户,该帐户拥有整个系统的最高权利,可以执行几乎所有操作。ROOT就是获取安卓系统中的最高用户权限,以便执行一些需要高权限才能执行的操作(包括卸载系统自带程序、刷机、备份、还原…...
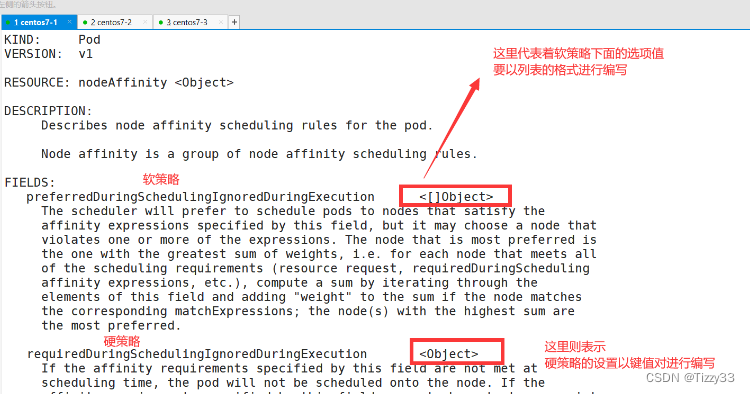
【云原生】k8s-----集群调度
目录 1.k8s的list-watch机制 1.1 list-watc机制简介 1.2 根据list-watch机制,pod的创建流程 2.scheduler的调度策略 2.1 scheduler的调度策略简介 2.2 Scheduler预选策略的算法 2.3 Scheduler优选策略的算法 3. k8s中的标签管理及nodeSelector和nodeName的 调…...
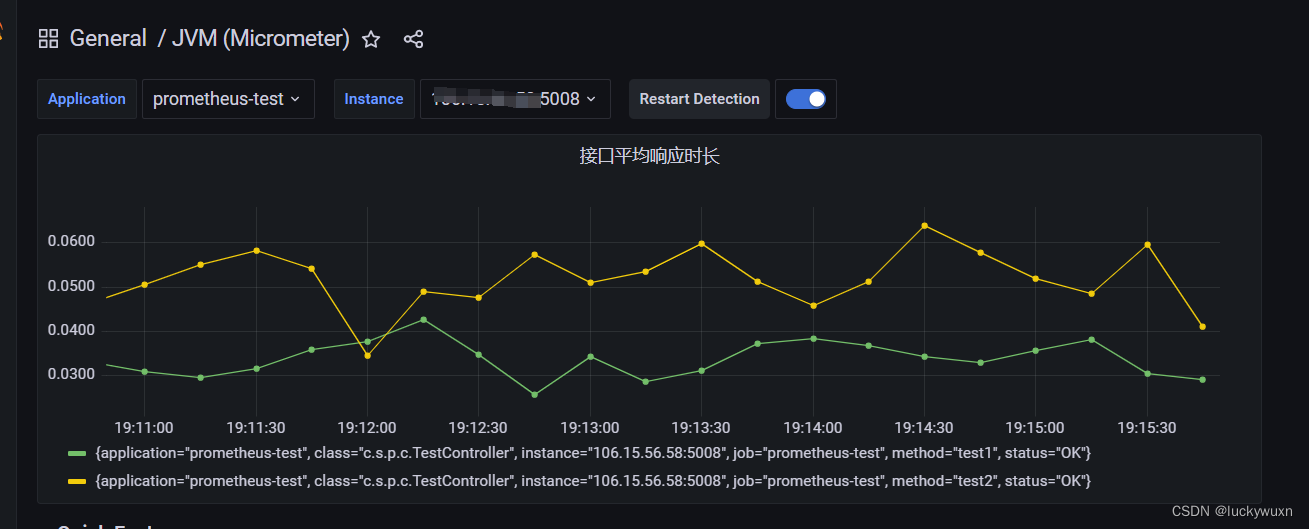
一键集成prometheus监控微服务接口平均响应时长
一、效果展示 二、环境准备 prometheus + grafana环境 参考博文:https://blog.csdn.net/luckywuxn/article/details/129475991 三、导入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter...
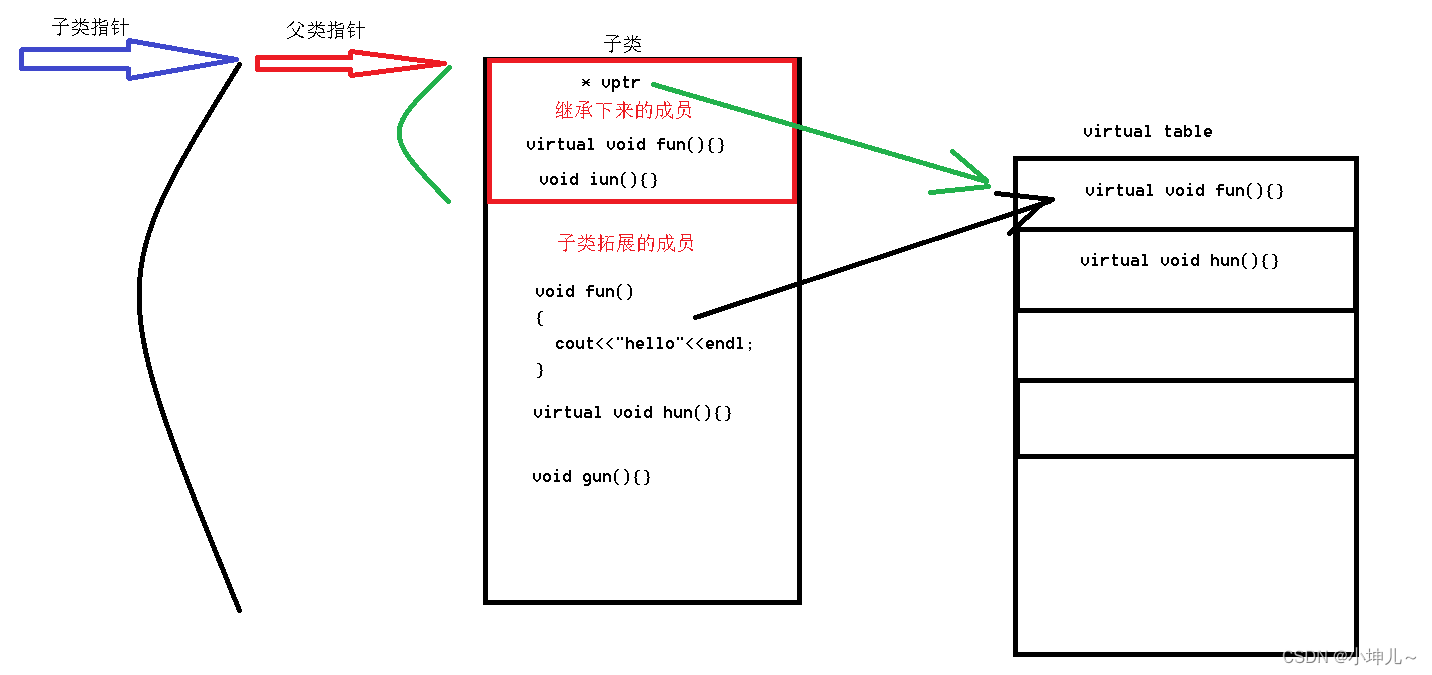
2023/9/13 -- C++/QT
作业: 1> 将之前定义的栈类和队列类都实现成模板类 栈: #include <iostream> #define MAX 40 using namespace std;template <typename T> class Stack{ private:T *data;int top; public:Stack();~Stack();Stack(const Stack &ot…...
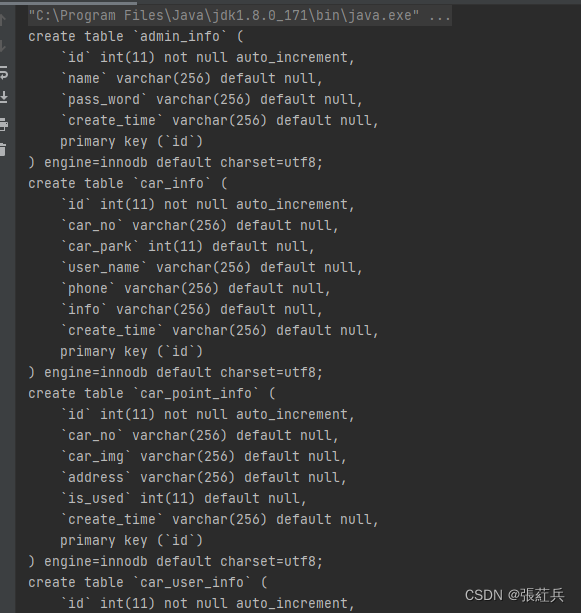
mybatis mapper.xml转建表语句
从网上下载了代码,但是发现没有DDL建表语句,只能自己手动创建了,感觉太麻烦,就写了一个工具类 将所有的mapper.xml放入到一个文件夹中,程序会自动读取生成建表语句 依赖的jar <dependency><groupId>org.d…...

封装使用Axios进行前后端交互
Axios是一个强大的HTTP客户端,用于在Vue.js应用中进行前后端数据交互。本文将介绍如何在Vue中使用Axios,并通过一个企业应用场景来演示其实际应用。 Axios简介 公众号:Code程序人生,个人网站:https://creatorblog.cn A…...

SOA、分布式、微服务
SOA: SOA是一种软件设计架构,用于构建分布式系统和应用程序。它将应用程序拆分为一系列松耦合的服务,这些服务通过标准化的接口进行通信,并能够以可编程方式组合和重用。SOA的目标是提高系统的灵活性、可扩展性和可维护性。 特点&…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
